基于差分法及试验联合确定非饱和土渗透系数的方法

江 明 王世梅 张兰慧 刘 凡

(三峡大学 土木与建筑学院， 湖北 宜昌 443002)

非饱和土渗透系数是非饱和土研究的重要参数之一，对于非饱和土渗透系数的求解，国内外学者从试验和理论两个角度展开了研究．试验方法[1-2]耗时过长，且其测得的非饱和土渗透系数的解的范围相对有限．因此大多数学者更倾向于理论研究，Frendlund等[3]在土水特征曲线的基础上建立了非饱和土渗透函数经验模型，缺点是计算过程复杂；孙大松等[4]建立了用分维值和进气值表示的土水特征曲线和渗透系数分形模型；Campbell模型[5]、Gardner模型[6]是以土的粒径分布、孔隙率等特性指标确定的土壤转换函数来间接估计非饱和土渗透系数的经验模型．然而上述模型都不具有普遍性，目前Van Genuchten[7]提出的VG模型在预测非饱和土渗透系数方面备受学者青睐．该模型简单且具有普遍适用性，其不足之处在于VG模型是经验公式，与工程实际略有偏差，且其表达的是渗透系数与基质吸力之间的关系，忽视了干湿循环作用下的滞后效应[8]，相关研究表明[9]，以体积含水量为自变量求得的渗透系数不受滞后效应的影响．因此本文基于有限差分法和一维垂直渗流试验，建立了一种以体积含水量为自变量求解非饱和土渗透系数的新方法，为今后非饱和土体渗透系数的预测提供一定的依据．

1 基于差分法的公式推导

1.1 一维垂直渗流控制方程

非饱和土水分运动基本方程的建立需要满足广义达西定律和质量守恒定律两个条件．广义达西定律是指单位时间内通过单位面积的水量即土体中液相的流速与其水力梯度成正比．

(1)

式中，V为水的流速，Kθ为渗透系数，ψ为总土水势，∂ψ/∂z为z方向的水力梯度．

理想状态下饱和土体中各位置体积含水量和基质吸力均相同，故饱和土体中的渗透系数K始终为常量．而非饱和土体中的渗透系数Kθ则随基质吸力或体积含水量的变化而变化．

非饱和土瞬态流形式中的水分流动满足质量守恒定律，可描述为单位体积土流入水的质量等于储存在该单位体积土中水的质量和流出水的质量之和．微元体内水的储存量可以用单位时间内的土体体积含水量的变化率表示．故瞬态水流可表示为：

(2)

式中，θ为体积含水量，t为时间．将(1)式代入(2)式可得一维非饱和土水分运动方程：

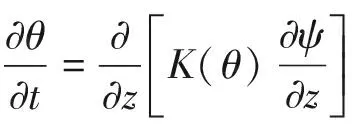
(3)

对非饱和土来说，溶质势和温度势极其微小，总土水势ψ忽略溶质势和温度势对土壤水分运动的影响．如果以原点为重力势能的零点，由于坐标正向向下，则重力势可表示为-z，总土水势为：

ψ=h-z

(4)

式中，h为基质势；-z为重力势．

令

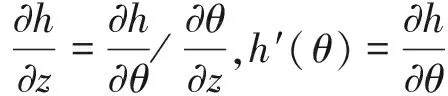
(5)

则式(3)变换为如下形式：

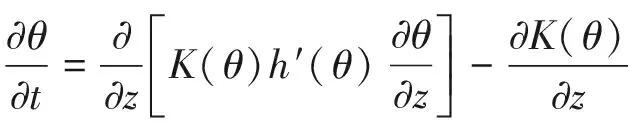
(6)

(6)式表达的即是一维垂直渗流控制方程，该方程仅仅只是适用于土体骨架不变形，且没有考虑生物或者化学作用对水流动影响的情况．

1.2 一维垂直渗流控制方程离散

由泰勒级数可得：

f(x+Δx)≈

(7)

f(x-Δx)≈

(8)

由(7)式得向前差商公式：

(9)

由(8)式得向后差商公式：

(10)

联立(7)、(8)式得中心差商公式：

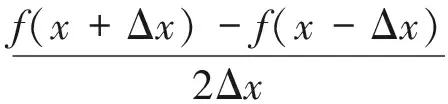
(11)

利用有限差分的思想对(6)式进行离散．将研究区域划分为矩形网格(如图1所示)，设i代表位置，j代表时间，时间步长为Δt，空间步长为Δz，对(6)式空间i和时间j两个维度进行离散．

图1 有限差分网格划分

因为θ=θ(t，z)，对于公式(6)，令

(12)

则(6)式化简为：

(13)

对(13)式进行中心差商：

其中：

(14)

(15)

(16)

(17)

将式(14)～(17)代入式(13)得渗流控制方程的差分格式(18)：

(18)

将式(18)写成非饱和土渗透系数的迭代格式(19)：

(19)

将式(19)写成简化模式(20)，p，q，r由(19)式因子算出．

(20)

2 试验及方法验证

开展了非饱和土一维垂直渗流试验及土水特征曲线试验，基于试验数据分别采用本方法及VG模型求解的方法获得了土样的渗透系数与体积含水量关系曲线，将两者进行对比，验证了该方法的可靠性．

2.1 一维垂直渗流试验

2.1.1 试验装置

模拟非饱和土一维垂直入渗的试验装置由供水系统、入渗土柱及采集系统组成，如图2所示．

图2 一维垂直渗流试验原理图

供水系统主要是由潜水泵将水箱内的蒸馏水抽入到高位水箱中，再通过溢流法将水缓慢输入土样中．入渗土柱试样装置内径300 mm，高600 mm，分别在50 mm、250 mm、350 mm、450 mm、550 mm处安置了1个体积含水量传感器(试验前已率定)．为了使水能够均匀入渗，在土样顶部与底部都装有反滤层，反滤层与土样之间用滤纸隔开，试样底部的天平能够实时称量流出水的质量．

2.1.2 试验土样

试验所用粘土过2 mm筛后，通过控制初始含水量与干密度获得土样的质量，将称好的土等分为3层，从下至上逐层均匀压实，装好的土样如图3所示．通过常规物性试验及常水头试验测得的指标见表1．

图3 装好的人渗土柱

表1 土常规物性指标

2.1.3 试验方案

在模拟恒定水头下非饱和土一维垂直入渗过程时，考虑到不同的水头高度只会影响土样中体积含水量的变化速率，为了避免高水头条件下体积含水量变化过快而捕捉不到详细的变化趋势，将水头高度设置为2.5 cm，控制数据采集间隔Δt为1 min，待试验数据在6 h内不再变化时，说明入渗土柱已经达到饱和．

整个试验过程持续时间为1 200 min，试验测得5个位置处体积含水量随时间的变化曲线如图4所示．

图4 不同深度体积含水量随时间变化关系曲线

从图4中可以分析得到以下结果：①深度越浅即离水土接触面越近的位置，含水量传感器的读数越先开始变化．②随着深度的增加，传感器的读数维持初始状态的时间越长．这是由于水分在土柱中的运移是从上部到下部的一个连续的由非饱和接近饱和的过程．土柱越往下，由非饱和状态到饱和状态所需要的时间越长．③随着时间不断延长，整个土柱的含水量都逐渐增加，达到稳定后整个试验土柱的含水量基本上一致，并且接近饱和．④5个位置的试样在试验达到稳定状态时的含水量都接近饱和，但是相比饱和含水量还有些许差距，这是由于试样并不是固、液两相，土体中存在没有随水流排出的气体．⑤随着深度的增加，不同位置饱和状态的体积含水量是逐渐减小的，但是减小的程度不是很明显．主要原因是土样制备是从下到上逐层压密的，从上到下土体的孔隙逐渐减小，饱和体积含水量不断减小，这是符合实际的．

2.2 土水特征曲线试验

为了与一维垂直渗流试验所用土样保持一致，控制土水特征曲线试验所用土样干密度为1.5 g/cm3，使用LAB523型压力膜仪(Tempe仪)分多级压力对3组平行试样进行试验，多级压力下测得的3组含水量求平均值，试验结果如图5所示．

图5 土水特征曲线

由于VG模型是目前采用最为普遍的土水特征曲线模型，故用Matlab中非线性拟合函数lsqcurvefit对土水特征曲线数据进行拟合，得到VG模型的相关参数，拟合曲线相关系数R2为0.930 37，拟合曲线如图5所示，VG模型参数见表2．

表2 VG模型相关参数

2.3 非饱和土渗透系数的求解

1)基于差分法及试验联合求解：

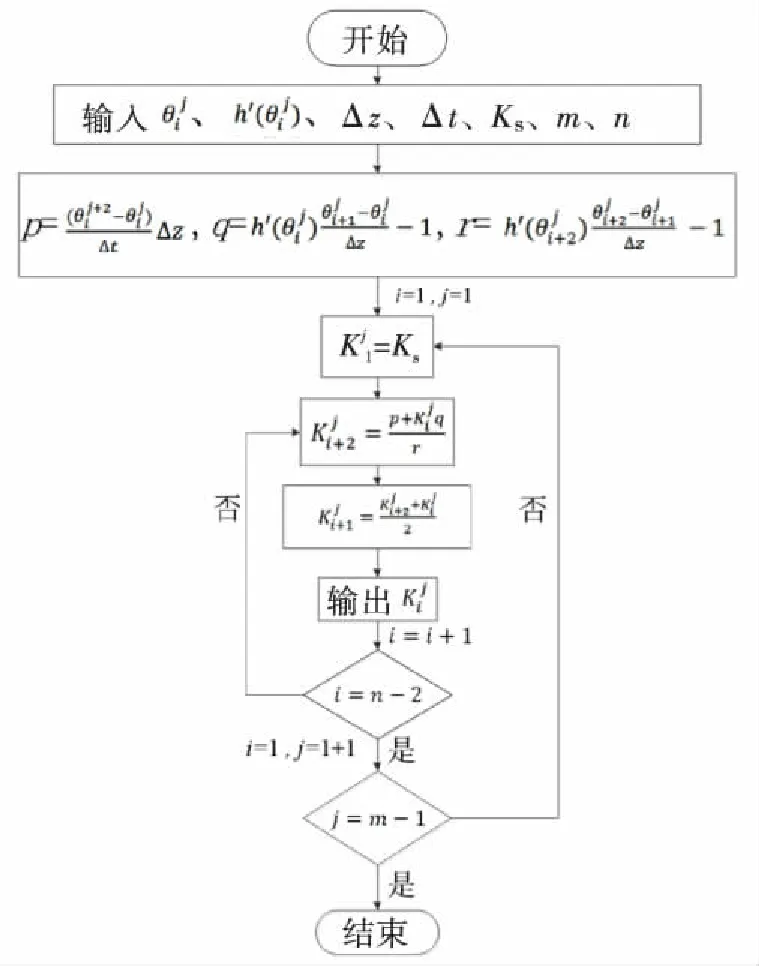
图6 迭代计算流程图

2)VG模型求解

利用土水特征曲线拟合得到的VG模型参数即可求解出非饱和土渗透系数Kvg，VG模型表达式如下：

(21)

(22)

Kvg=KsΦ0.5[1-(1-Φ1/m)m]2

(23)

式中，θ为计算时段土壤体积含水量，h为基质势，α，m，n为经验拟合系数，θr为残余体积含水量，θs为饱和体积含水量，Ks为饱和渗透系数，Kvg为相对应θ的渗透系数．

将差分格式求出的计算值Kt与VG模型所求值Kvg进行对比分析，如图7所示，两种数据变化的趋势基本相同．

图7 计算值与VG模型求解值对比图

2.4 误差分析

对两种方法求出的非饱和土渗透系数进行趋势对比后还需要分析两者之间的误差．

由于非饱和土渗透系数值的变化范围过大，跨越6个数量级，一般的均方差无法较好的判定二者之间的差异情况．为了定量分析两种方式所求值的误差，定义差分格式计算值与VG模型计算值比值平均值[10]为GMER．

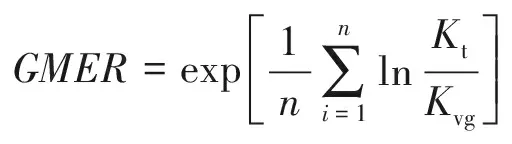
(24)

式中，n为分析样本数，Kt为差分格式计算值，Kvg为VG模型模拟值．按照式(24)对差分格式计算值进行误差分析，评判标准为GMER越接近于1.0，误差越小，拟合的精度越高．

引用王成华等[11]对几种经验公式模型的误差分析数据与差分格式的误差分析作对比，见表3．

表3 8种经验公式模型GMER值

由表3可知，Vereecken、Rawls(2)、Wosten(1)、Wosten(2)模型的GMER值均小于1.0，Campbell、GHM、Rawls(1)模型的GMER值均大于1.0，Wosten(1)模型计算得到的GMER值0.94与1.0最为接近，故其拟合误差最小．本文GMER值3.84，相比于上述3种GMER值大于1.0的模型，其拟合误差最小．对比发现，通过差分格式求解非饱和土渗透系数的方法具有一定的可靠性．

由于差分格式求出的是数据点，不能完整的表示渗透系数值，因此对差分格式所求值进行拟合得到了相关函数曲线．拟合函数表达式为：

lg(K)=a+b*θ

(25)

式中，a、b均为参数，相关系数R2为0.999 2．

图8 渗透系数与体积含水量的关系曲线

由图8表明a，b参数均与土的颗粒组成与内部结构有关，同一体积含水量状态下，a参数越大，渗透系数越大，b参数与渗透系数的增长速率有关，b参数越大，渗透系数增长越快．

3 结 论

本文提出了基于一维垂直渗流控制方程差分求解及非饱和渗透性试验联合确定非饱和土渗透系数的新方法．主要得到了以下结论：

1)推导了一维垂直渗流控制方程的差分格式，该差分格式只需由试验测得相关参数就可以通过Matlab编程求解出非饱和土渗透系数．

2)试验粘土渗透系数的对数lg(K)与体积含水量θ的分布呈直线变化规律．

3)用差分格式与VG模型两种方法求解的非饱和土渗透系数较为一致，用GMER算出的误差较小，认为本文提出的求解非饱和土渗透系数的新方法具有一定的可靠性，对非饱和土体渗透系数的预测具有一定的借鉴意义．