库水位骤降联合降雨边坡稳定敏感性分析

张珂峰

(南通开放大学 建筑工程学院， 南通 226000)

库水位骤降是诱发库区边坡失稳的重要因素[1-2]，库水位骤降会导致边坡体内部孔压变化[3-4]，有效应力降低[5-6]，从而导致滑坡．国内外因库水位骤降而导致的滑坡灾害不胜枚举，如意大利的Vajoint坝[7]，于1963年在库水位骤降工况下发生了垮塌；我国三峡水库在库水位骤降运行过程中，库区边坡也多处发生了局部的失稳现象．库水位骤降导致滑坡产生的危害主要体现在：①损坏库区周围的基础设施；②影响水库的正常运行；③对库区周围居民的生命财产造成威胁．因此，研究库水位骤降下的边坡渗透稳定性意义重大．

对于库水位骤降下的边坡渗透稳定性，国内外已有较多研究：试验方面，徐楚[8]利用由标准砂、滑体土、膨润土和水溶液混合制成的土坝模拟了在不同库水位骤降速率下的变形特征；李子晗[9]对高水位长期浸泡堤防在库水位变动下位移及稳定性进行了监测．数值模拟方面，余志刚[10]利用Abaqus软件对边坡岩体在无裂隙、有裂隙、增大渗透系数、单独降水及升水等5种条件下进行了流固耦合数值模拟；胡致远[11]利用Geo-slope软件对库水与降雨联合作用下藕塘滑坡稳定性进行了研究．以上数值模拟及试验对库水位变动下的边坡稳定性规律的认识提供了一定的参考，但是实际情况中边坡的材料力学参数具有空间变异性，对于库水位骤降下的边坡各种材料的敏感性分析却鲜有研究．

本文以三峡库区某边坡体为例，基于区间敏感性理论，研究了库水位骤降下边坡体不同材料参数变动下渗透稳定敏感性，为定量化认识不同参数对于边坡渗透稳定性的影响提供了一定的参考．

1 非饱和渗透稳定性理论

1.1 非饱和渗透理论

非饱和渗流方程可以表示为如下形式：

(1)

式中，kij为渗透张量；kr为相对渗透系数；hc为位置水头；xi，xj为位置坐标；Q为源汇；C(hc)为与位置水头相关的函数；Ss为容水度；θ为体积含水量；t为时间．

土水特征曲线(SWCC曲线)采用Fredlund & Xing模型[12]，方程表示如下：

(2)

式中，θw是土体的体积含水量；θs是饱和含水量；φ是负压；a，m，n为拟合参数．其中：

a=φi

(3)

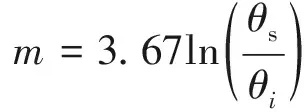
(4)

(5)

式中，φi是拐点吸力；s是拐点斜率．

渗透系数函数根据式(2)计算出的体积含水量，利用下式计算：

(6)

式中，kw为含水量对应的渗透系数；ks为饱和渗透系数；y为虚拟变量；i为数值间距；j为最小负孔压；N为最大负孔压，Ψ为第j步的负孔压；θ0为起始值．

1.2 非饱和抗剪强度理论

非饱和抗剪强度理论采用Fredlund双应力变量公式[13]：

s=c′+σntanφ′+(ua-uw)tanφb

(7)

式中，c′与φ′分别为粘聚力和有效内摩擦角；σn为法向总应力；ua为空气压力；uw为孔压；φb表征提高的强度．

1.3 非饱和边坡抗滑稳定公式

非饱和边坡抗滑稳定公式如式(8)：

Fs=

(8)

2 区间敏感性分析原理

区间敏感性方法是一种利用变量的参数范围为基准，通过敏感性分析原理建立的一种方法[14]．假设边坡不同的物理力学参数构成集合A，边坡的评价指标构成集合B，则集合A到集合B存在如下关系：

(9)

式中，δij是影响权重因子．

(10)

3 工程实例

3.1 计算模型及边界

某滑坡体位于我国西南部，距离挡水坝约45 km，正常蓄水位为175 m，死水位为145 m，计算模型如图1所示，模型网格剖分图如图2所示．计算工况为库水位从175 m骤降至145 m，骤降速率为0.5 m/d，降雨强度为0.01 m/d．设置上部监测点，中部监测点以及下部监测点来实时监测边坡不同位置的变形量．

图1 计算模型

图2 模型网格图

边界条件设置如下：1)dc为降雨入渗边界；2)cb为库水位变动边界；3)ab，de为不透水边界；4)ae为190 m定水头边界．

3.2 材料参数

材料本构采用摩尔-库伦准则，根据不同地质勘探结果，选取滑体材料的弹性模量E，粘聚力c，内摩擦角φ，泊松比μ，渗透系数k这5个参数的变化范围作为参考序列，上部监测点位移，中部监测点位移，下部监测点位移及最小安全系数作为评价指标，参考序列参数的范围见表1．

表1 参考序列指标

3.3 计算结果

根据有限元计算结果，结合敏感性区间分析理论的分析方法，获得模型参数对评价指标的影响大小区间见表2，评价指标的可行域区间见表3，参数对评价指标的敏感性因子矩阵见表4．

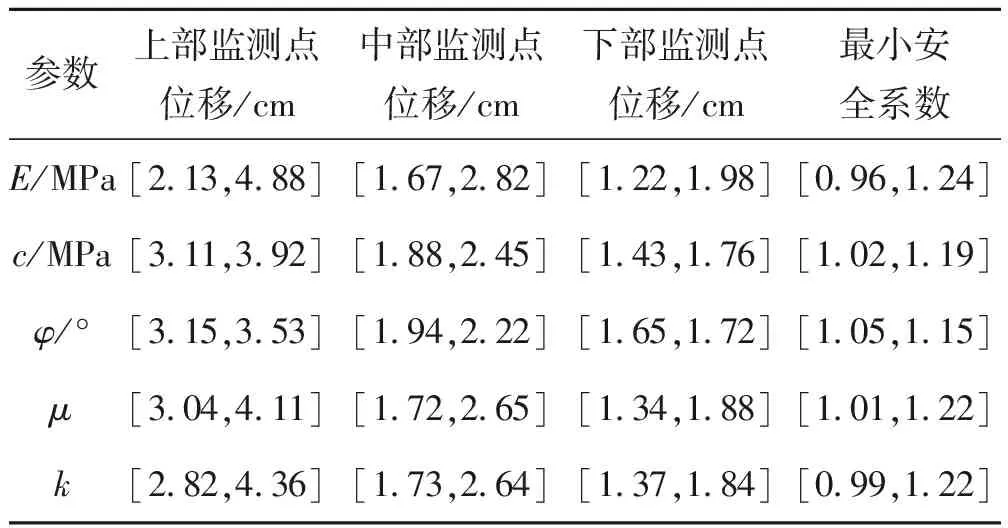
表2 模型参数对评价指标的影响大小

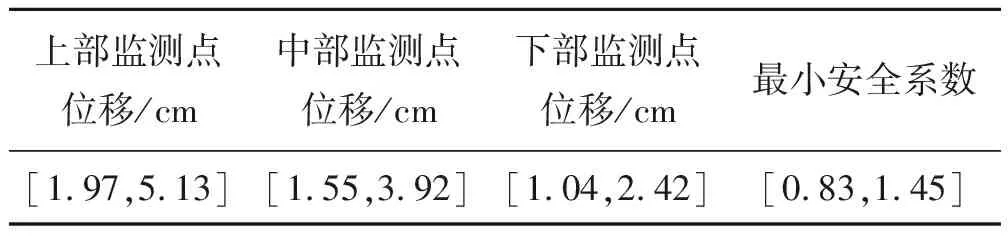
表3 评价指标的可行域

表4 敏感性因子矩阵

从表4可得出不同边坡参数(弹性模量E，粘聚力c，内摩擦角φ，泊松比μ，渗透系数k)对监测点位移及最小安全系数的影响大小，结论如下：

1)弹性模量与渗透系数对上部监测点的位移影响最大，但粘聚力、内摩擦角及泊松比对各个工况的影响差异则不大．

2)同一工况不同参数下，敏感性大小顺序为：弹性模量、渗透系数、泊松比、粘聚力、内摩擦角，与文献[15-16]的研究结论一致．

4 结 论

1)区间敏感性分析可以快速的获得边坡各个物理力学参数对边坡变形及稳定性的影响大小，与已有研究成果一致，可以指导由于边坡物理力学参数的空间变异性导致的数值模拟中材料参数的取值问题，同时为边坡在库水位联合降雨条件下的渗透稳定性分析提供了一个很好的案例．

2)库水位骤降联合降雨条件下，弹性模量与渗透系数对上部监测点的位移影响最大，但是粘聚力、内摩擦角及泊松比对各个工况的影响差异则不大．

3)对于同一评价指标来说，影响大小排序为：弹性模量、渗透系数、泊松比、粘聚力、内摩擦角．