坝头形式对丁坝附近水流结构的影响分析

方 强 黄赛花 王继保 陈艳超

(1. 三峡大学 水利与环境学院， 湖北 宜昌 443002； 2. 浙江水利水电学院 水利与环境工程学院， 杭州 310018)

丁坝是治河、水陆交通建设及滩涂围垦等工程中使用最广泛的建筑物之一，具有束窄水流冲刷河槽、稳定河岸和保护水生态多样化等作用．胡旭跃等[1]探讨勾头长度对丁坝附近流速场的影响．于守兵等[2]采用物理试验和数值模拟相结合的方法研究端坡系数对丁坝附近水流结构的影响作用．程年生等[3]探讨边坡的存在对丁坝回流特性的影响．郑艳等[4]建立二维数学模型研究宽浅河道中丁坝长度对回流长度的影响．陆晶等[5]探讨挑角对淹没丁坝周围底床冲刷的影响．任云等[6]以长江口南支为原型，研究双向流条件下丁坝水流特性．喻涛等[7]分析不同坝身横断面型式对丁坝稳定性的影响．王振等[8]运用Sufer软件研究坝长和挑角与河床冲淤量间的相关关系．樊新建等[9]基于Fluent研究水力插板透水丁坝水流结构对透水率的响应规律．此外，还有不少学者[10-12]研究勾头丁坝对弯曲河道水流结构的影响．

上述研究主要为坝长、挑角等丁坝设计参数和水流条件对丁坝附近水流特性及床面冲淤的研究，但关于坝头形式对丁坝附近水流特性的研究比较少．坝头形式是丁坝设计参数之一，不同形式的坝头会导致丁坝附近水流的相应变化．本文通过RNGk-ε湍流模型模拟丁坝附近水流，探讨不同坝头形式对丁坝附近水流结构的影响．

1 数学模型

1.1 控制方程

连续方程：

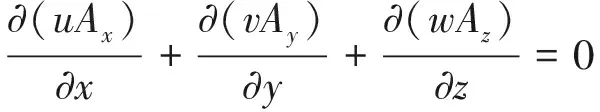
(1)

动量方程：

(2)

(3)

(4)

式中，u、v、w为各方向上的速度分量；Ax、Ay、Az为各方向上可流动的面积分数；VF为可流动的体积分数；ρ为流体密度；p为流体微元上的压力；Gx、Gy、Gz为各方向上的重力加速度分量；fx、fy、fz为各方向上的粘滞力分量．

1.2 湍流模型

与标准k-ε湍流模型相比，RNGk-ε湍流模型考虑低雷诺数效应和旋流修正，可更精准地模拟湍流．丁坝附近水流流态复杂，水流扰动剧烈，因此采用RNGk-ε湍流模型进行丁坝三维数值模拟．

紊动能k方程：

(5)

紊动能耗散率ε方程：

(6)

2 数学模型验证

2.1 Tominaga丁坝模型

本文基于Tominaga[13]丁坝实验进行数学模型验证．水槽长8.0 m、宽0.3 m，丁坝长0.15 m、宽0.03 m、高0.05 m，丁坝迎流面距水流入口4.0 m处．槽内平均水深约0.09 m，未受干扰区行近水流流速约为0.133 m/s．按照1∶1比例建模，采用结构网格进行划分，并局部加密网格．初始水位为0.09 m；入口边界流速设定为0.133 m/s；出口边界设定自由出流；顶部设定压力边界，相对压强为0；水槽两侧及底部设定固壁边界．

2.2 模型验证

选取丁坝上、下游各一个位置处的相对流速进行流速验证，相对流速即流速与行近水流流速之比．相对流速验证位置分别为x=4.00 m，z=0.07 m；x=4.05 m，z=0.02 m(坐标原点位于丁坝迎流面坝根处)．由图1可见，计算结果与实测数据吻合较好，说明采用RNGk-ε湍流模型模拟丁坝附近水流流态是可行的．

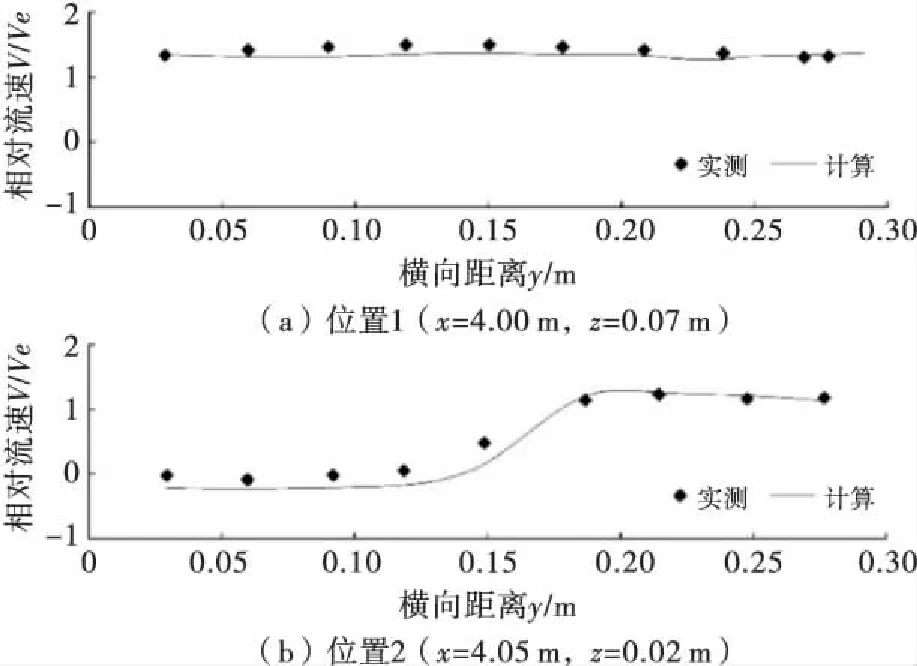
图1 位置1、2相对流速验证

3 坝头形式对丁坝水流特性的影响

3.1 丁坝形式及计算条件

本研究建立3种坝头形式的正挑丁坝，以此探讨坝头形式对丁坝附近水流结构的影响．丁坝长度15 cm，坝身宽度5 cm，高度15 cm，分别为方形直头丁坝、圆弧直头丁坝、扇形直头丁坝．其中圆弧直头丁坝坝头为半径2.5 cm的半圆，扇形直头丁坝坝头为角弧度135°、半径4 cm的圆弧．模拟对象为水槽概化模型，长8.0 m，宽0.5 m．进口边界水流流速为0.15 m/s，水深0.10 m；出口边界设定为自由出流；水槽两侧及底部设定为固壁边界．

图2 丁坝模型(单位：cm)

3.2 网格划分及独立性验证

网格质量及划分方式将会对计算结果产生一定影响[14-15]．为保证计算结果准确性，需验证网格独立性．以方形直头丁坝为例，分别建立69.09万、89.08万、133.05万和167.89万等4套网格进行数值模拟．选取三个特征点处的流速进行对比分析，其中特征点位置为x=2 m，z=0.01 m．由表可知，网格数量不少于89.08万时，特征点流速相对变化率均小于2%，在误差允许范围内．因此，选取网格数量为89.08万的数学模型进行相关问题研究．

表1 网格独立性验证(x=2 m，z=0.01 m)

3.3 自由液面变化

选取x=-0.01 m，y=0.16 m两个断面进行自由液面横、纵向变化分析．由图3可知，圆弧直头丁坝和扇形直头丁坝附近自由液面变化趋势基本一致，与方形直头丁坝略有不同．水流流经丁坝时，受坝头形式及对水流扰动程度的影响，方形直头丁坝附近自由液面降至最低处的位置较其余两种形式丁坝靠后，这在横向上表现尤为显著．

图3 自由液面分布

3.4 流速分布

图4 流速等值线分布图(z=0.01 m，单位：m/s)

3.5 回流场尺寸分析

有关资料表明，坝后回流结构与坝头形式密切相关．选取表层平面(z=0.08 m)分析坝头形式对回流结构的影响，丁坝上、下游流线分布如图5所示．

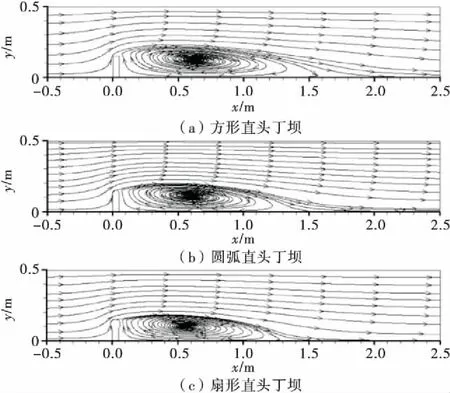
图5 丁坝上、下游流线分布(z=0.08 m, l=0.15 m)

由图可知，非淹没情况下，水流流经坝轴断面后，一部分水流继续前进，另一部分水流在丁坝下游形成一个顺时针旋转的回流区．其他条件相同的情况下，方形直头丁坝、圆弧直头丁坝和扇形直头丁坝的回流长度为11.78l、9.76l和9.03l(l为丁坝长度)，最大回流宽度为1.67l、1.47l和1.48l．可以看出，其他条件相同时，曲线形直头丁坝坝后回流长度和束窄作用均比方形直头丁坝小，其中回流长度尤为明显．扇形直头丁坝与圆弧直头丁坝的差异主要为回流长度，最大回流宽度几乎没有变化．

3.6 漩涡分析

图6为丁坝下游横断面水流流场图，其中横断面位置距离丁坝迎流面0.4 m．由图6可知，各丁坝下游均存在横轴漩涡．方形直头丁坝横断面流场与圆弧直头丁坝横断面流场相似，均在水槽底部距右侧边壁0.15～0.2 m间形成一个顺时针旋转的漩涡．扇形直头丁坝横断面流场与前两种形式丁坝不同，由于该坝头曲线段存在显著的曲率拐点，水流流经坝轴断面后形成两个横轴漩涡，并且漩涡中心较靠近水槽中部，其中距水槽右侧边壁约0.16 m处形成顺时针横轴漩涡，另一个则为逆时针横轴漩涡．

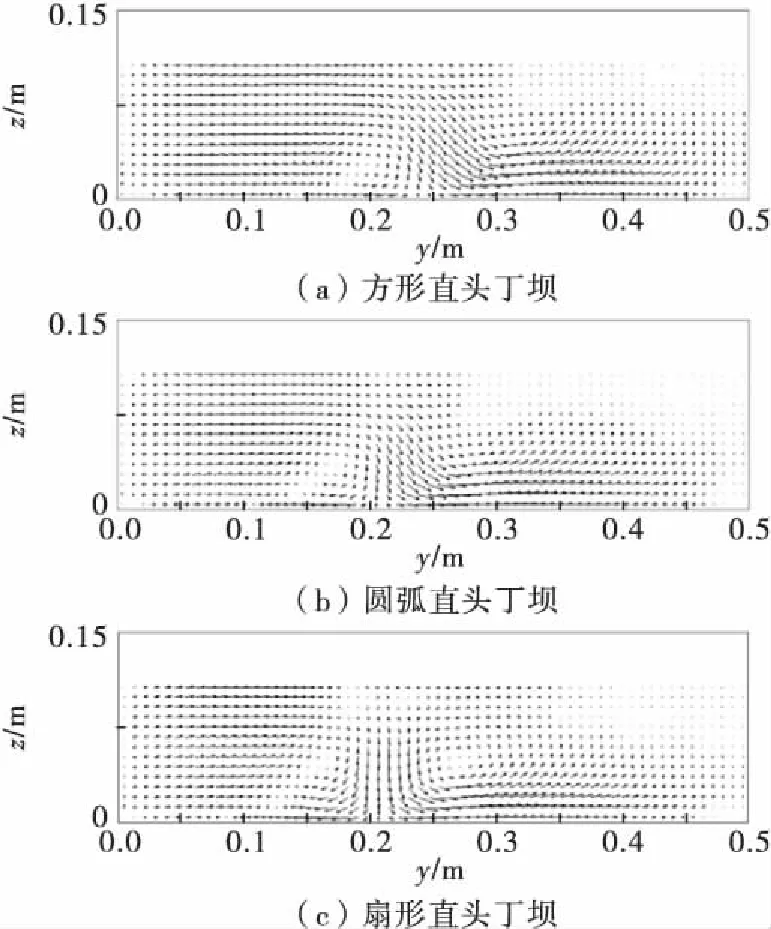
图6 横断面水流流场

3.7 紊动能影响分析

坝头是涡源形成的地方，漩涡的随机移动、破碎和合并使丁坝下游有明显的紊动分布．坝头形式会直接影响丁坝与水流的衔接方式，进而改变丁坝下游紊动分布情况．图7为各坝头形式丁坝表层平面(z=0.08 m)的紊动分布图．由图可知，丁坝上游和坝头周围紊动能均较小，较大值主要分布在丁坝下游0.5～2.0 m范围内．方形直头丁坝、圆弧直头丁坝和扇形直头丁坝的紊动能最大值依次减小，分别为2.87×10-3、2.37×10-3和2.22×10-3J，并且紊动区域呈现出向上游移动的趋势．这主要是因为曲线形坝头能更为平稳地过渡水流，较方形坝头对水流的扰动更小，从而减小坝后紊动强度．与圆弧直头丁坝相比，扇形直头丁坝紊动能最大值及各紊动值影响范围进一步减小，究其原因是扇形直头丁坝坝后形成两个不同方向的横轴漩涡，使其相互制约和抵消．

图7 紊动能分布(z=0.08 m)

4 讨 论

其他条件相同的情况下，坝头形式的改变对丁坝附近水流的影响较为显著．从坝头形式对底层平面流速、回流场尺寸和紊动能的影响来看，扇形直头丁坝能更为平稳地过渡水流，对水流的扰动程度最小，其次为圆弧直头丁坝，最后为方形直头丁坝．由于方形直头丁坝底层平面高流速区域较大，对水流的扰动程度也相应较大，在实际航道整治工程中采用方形直头丁坝更有利于冲刷河床，维持航道水深．另外，方形直头丁坝的回流长度和束窄宽度比曲线形直头丁坝大，在实际工程中可采用较短的方形直头丁坝替代曲线形直头丁坝，达到相近的有效影响范围．这对降低工程造价具有一定意义．

5 结 论

运用RNGk-ε湍流模型进行三维丁坝数值模拟，研究坝头形式对丁坝附近水流结构的影响，得到如下结论：

1)扇形直头丁坝附近自由液面变化趋势与圆弧直头丁坝相似，方形直头丁坝附近自由液面降至最低处的位置较其他两种形式丁坝靠后．

2)坝头形式对丁坝近底床流速影响显著．

3)曲线形直头丁坝的有效影响范围较方形直头丁坝小，其中坝后回流长度尤为明显，而圆弧直头丁坝的影响程度与扇形直头丁坝相差不大．

4)各丁坝坝后均形成横轴漩涡，方形直头丁坝横断面流场与圆弧直头丁坝横断面流场类似，扇形直头丁坝坝后形成两个不同方向的横轴漩涡．

5)曲线形坝头能更为平顺地过渡水流，方形直头丁坝、圆弧直头丁坝、扇形直头丁坝的紊动能最大值依次减小，并且紊动区域呈现出向上游移动的趋势．