圆锥曲线动点问题探究

◎ 叶婷婷

此题为笔者所在学校的一次月考题，得分率很低，图1中P、Q两点分别在椭圆和圆上运动。随着动点的移动，我们发现线段|PQ|与|PF2|的长度都在发生变化，两个一起变化的时候，学生就束手无策了。那么，教师在讲课过程中就应该让学生先研究其中一个动点。因此，先把点Q看成定点，这样此题就变成了求动点P到两个定点之间的距离之和的最大值。根据三角不等式和椭圆的定义有，|PQ|+|PF2|=|PQ|+2a-|PF1|=|PQ|-|PF1|+6≤|QF1|+6(图2)。

图2

根据图2，当点P在线段|QF1|的延长线与椭圆交点P1的位置时，|PQ|+|PF2|取得最大值|QF1|+6。接下来，我们再看点Q的运动。点Q是圆上的动点的，要使|QF1|取得最大，点Q在F1C的延长线且与圆C相交的点Q1时：

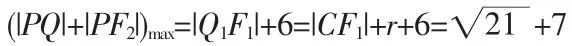
然而，在解题过程中，其实很多学生并不能想到先把其中的点Q当成定点。“Q点在圆周上运动，怎样才能想到把它先当做定点呢？”如果我们仔细研究Q点的轨迹，它是在一个以C为圆心的圆周上运动。此圆圆心为C，假设它的半径r不确定，当我们把此圆的半径变得无穷小的时候，圆就压缩成了一个点C(图3)，此时，点Q与点C重合，我们有|PQ|+|PF2|=|PC|+|PF2|，再根据椭圆定义有|PC|+2a-|PF1|=|PC|-|PF1|+6，根据三角不等式找到点P满足的位置。这样点P的位置找到之后，再考虑把圆的半径r慢慢变大，再考虑对应点Q的位置，就很容易理解了。这里采取的极限思想其实就是把圆的半径无穷小，将圆压缩成一个点，让学生更好地先找到动点P的位置。

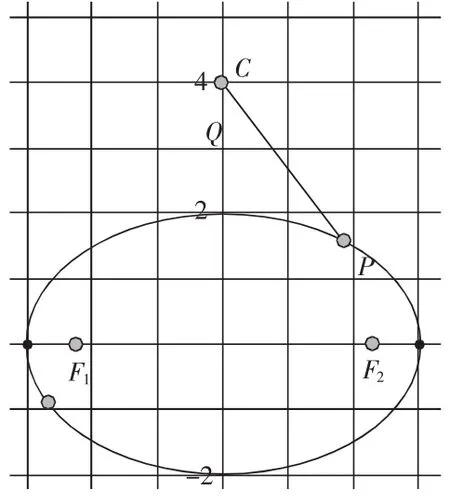
图3

其实，本题除了考虑把圆压缩成一个点这一极限方法外，我们还可以考虑把椭圆压缩(图4)，椭圆压缩扁了之后就是一条线段F1F2，长度为6，点P 在 F1F2上运动且满足：|PF2|=6-|PF1|，|PQ|+|PF2|=|PQ|+6-|PF1|≤|QF1|+6。

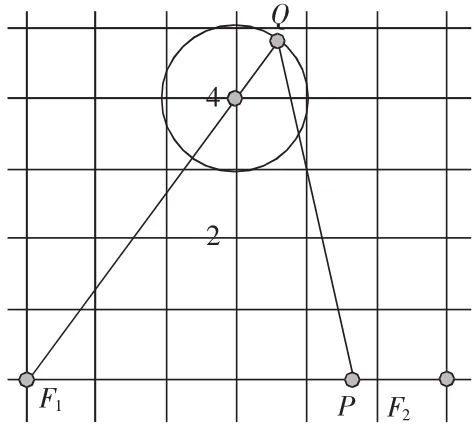
图4

此时，我们很容易知道Q在F1C的延长与圆的相交点处。找到Q点的特征之后，再慢慢把线段还原成椭圆，也就能够找到点P的位置，相信这两种极限思想(圆压缩成点，椭圆压缩成线段)，都能够有助于学生更加深刻地理解题目。类比椭圆和圆取极限的压缩，双曲线压缩之后是两条射线。

总之，用极限的思想把圆锥曲线特殊化，利用极限位置找到动点取到最值时的特征，再将圆锥曲线还原，不乏是我们平时研究试题一种巧妙的方法，也是我们探索该类问题的一种新颖的路径。