由教材一例题引发的思考

◎ 武占斌

人教版A必修二129页例3：已知圆C1：x2+y2+2x+8y-8=0，C2：x2+y2-4x-4y-2=0，试判断两圆的位置关系。

在解题过程中，当两圆方程相减得x+2y-1=0此直线为两圆公共弦所在的直线。试想C2将变为C3：x2+y2-4x-4y+4=0时，C1与C3相离，此时C1与C3的方程之差x+2y-2=0，此直线和C1与C3都相离，它又有何几何意义？

为了解决此问题，需要从圆幂定理和根轴谈起。

一、点到圆的幂

设P为圆O所在平面内任意一点，PO=d，圆O的半径为r，则d2-r2就是点P对圆O的幂，记k=d2-r2(k∈R)。

二、圆幂定理

是平面几何中的一个定理，是相交弦定理、切割线定理及割线定理(切割线定理推论)的统一，例如如果交点为P的两条相交直线与圆O相交于A、B与C、D，则PA·PB=PC·PD。

三、过点P任作一条直线与圆O交于A、B，则由圆幂定理得PA·PB=k2，如图：(1)(2)

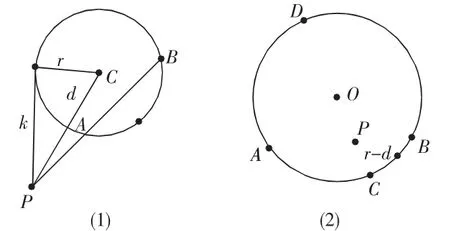
四、到两非同心圆等幂的点的轨迹是与此两圆的连心线垂直的一条直线，这条直线称为两圆的根轴，可用圆幂定理来证明

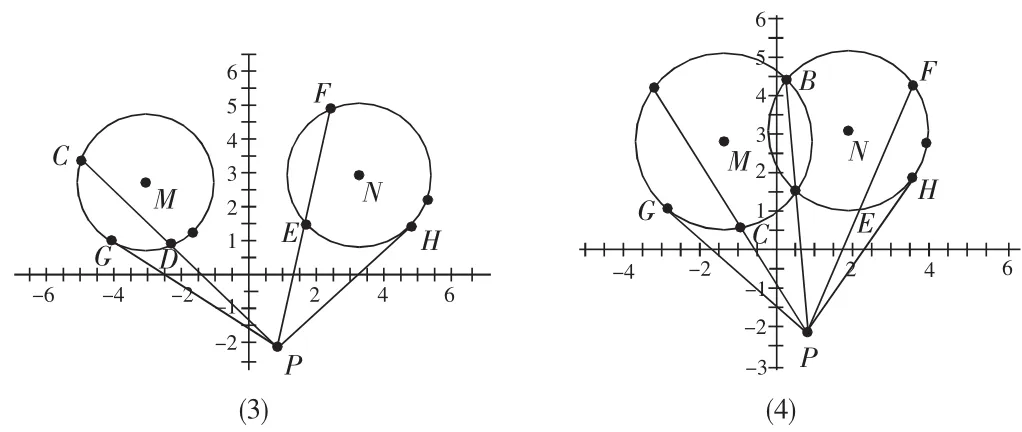
圆 M：x2+y2+D1x+E1y+F1=0，圆设P(x，y)为平面上一动点，过点P的直线与圆M交于C，D，与圆N交于E，F，PG，PH分别与圆M，N相切于点G，H。

当两圆相交于 A，B 两点，PG2=PC·PD=PA·PB=PE·PF=PH2，故等幂点的轨迹为AB直线(与连心线垂直)。如图：(3)(4)

当两圆相离时 PG2=PC·PD=PE·PF=PH2，所以 PG2=PH2，即，也即

所以(D1-D2)x+(E1-E2)y+(F1-F2)=0即为两圆的根轴方程。

当非同心两圆内也有类似规律，两同心圆方程作差(F1-F2)=0，所以F1=F2此时两圆重合。

可见，两非同心圆的根轴方程为两圆的方程之差所得的二元一次方程，显然与连心线垂直。当两圆相切时根轴为两圆的一条公切线，当两圆相交时为两圆公共弦所在直线，当两圆等大时为两圆的对称轴，当两圆相离时为平面上圆外点引两圆切线，切线长相等的点的轨迹。

这些理论在处理直线与圆有关的问题中有着广泛的应用。

例1：(必修二144页A组第6)已知圆x2+y2=4和圆x2+y2+4x-4y+4=0关于直线l对称，求直线l的方程。

分析：两圆相交对称轴即为两圆公共弦所在直线(根轴)x2+y2+4x-4y+4-(x2+y2-4)=0即：x-y+2=0

例2：①(必修二133 页第7)求与圆C：x2+y2-x+2y=0 关于直线 l：x-y+1=0对称的圆的方程。②(必修二144页A组第7)求与圆C：(x+2)2+(y-6)2=1关于直线3x-4y+5=0对称的圆的方程。

分析：这两题与例1是逆向思维问题：已知一圆和根轴的方程求对称圆，两方程作差便可得对称圆的方程吗？由于方程x-y+1=0尽管表示根轴，但不一定是两圆作差后的初始结果。为此有以下解法。

①x2+y2-x+2y-λ(x-y+1)=0，x2+y2-(λ+1)x+(2+λ)y-λ=0 此圆圆心为又它们的中点在 x-y+1=0 上，所以，所以所求圆的方程为：x2+y2+4x-4y+4=0②同理。

例3：(2013年山东高考理科第9题)过点P(3，1)作圆M：(x-1)2+y2=1的两条切线，切点分别为A，B，则直线AB的方程为()。

A.2x+y-3=0 B.2x-y-3=0 C.4x-y-3=0 D.4x+y-3=0

分析：以PM为直径的圆(x-3)(x-1)+(y-1)(y-0)=0，与圆作差得2x-y-3=0为两圆的根轴，即为所求。

对知识无论做多深入的探究都不过分。数学是一种追求思维深度的艺术，宁静方能致远。