三种漂浮式风力机调谐质量阻尼器稳定性控制研究

黄致谦，丁勤卫，李 春

(上海理工大学 能源与动力工程学院，上海 200093)

海上风能较于陆上风能，具有湍流强度小、风速高及不占用土地资源等优点，使得海上风电产业不断发展，在我国能源产业中占据越来越重要的位置[1]。可见未来风电场的发展趋势必然是“由陆地向海洋、由浅海到深海、由固定式基础向漂浮式平台”[2]。由于技术和成本的限制，现阶段海上风电场都普遍建设在浅海区域，风力机也大多采用固定基础[3]。对于深海区域(水深超过60 m)，从安全和经济性角度分析，必须要使用漂浮式平台[4]。目前，国内外普遍认可的，根据漂浮式平台结构及获取稳定性方式的不同，主要分为以下3类：驳船型结构(Barge)、浮柱型结构(Spar)以及半潜型结构(Semisubmersible，Semi)[5]。漂浮式平台主要依靠压舱物的恢复力矩、锚链拉力以及水线面的面积矩维持稳定性。

漂浮式风力机在役于海上，同时受风、浪及流等复杂环境载荷的联合作用，又因其漂浮基础不固定，导致其一直处于受力不平衡、非定常运动状态，造成了其动态响应的复杂性[6]。复杂的动态响应进而影响漂浮式风力机的正常工作，降低发电效率，引发塔架和叶片的变形，甚至会导致塔架屈曲、平台倾覆。因此如何高效、经济地保证漂浮式风力机在复杂海洋环境下安全稳定地工作，成为海上风电产业建设中亟待解决的一个重要问题[7]。为此，许多学者对漂浮式风力机的稳定性控制进行了研究。有学者提出通过加强漂浮式风力机主体结构(平台、塔架等)的强度，如提高材料强度等级、加大主体结构的截面尺寸等，但这将导致漂浮式风力机的成本大幅度增加，也存在许多技术难题[8]。Namik等[9]采用独立变桨技术，通过改变叶片桨距角控制漂浮式风力机的稳定性。Lackner[10]研究通过改变电机扭矩大小来达到减小漂浮式风力机的运动及载荷的目的。上述两种方法基于现有风力机控制系统，虽能对漂浮式风力机起到一定的控制作用，但仍存在叶片、塔架根部疲劳载荷过大等致命问题。

随着对漂浮式风力机稳定性研究的不断深入，结构被动控制(调频质量阻尼器、调频液体阻尼器等)开始应用于漂浮式风力机[11]。赵斌等[12]建立风力机调频质量阻尼器(Tuned Mass Damper，TMD)控制模型，并对模型进行振动台试验，通过比较风力机的位移和加速度时程曲线，发现TMD对风力机稳定性具有良好的控制作用。Luo等[13]将风力机结构简化为质量块，使用调频液体阻尼器(Tuned Liquid Column Damper，TLCD)对风力机的纵荡进行稳定性控制，但因其模型过于简化且只能考虑单自由度的振动，无法对风力机塔架及平台纵摇、垂荡等主体结构的主要运动形式进行研究。Matthew等[14]为研究TMD对漂浮式风力机稳定性的作用，使用FAST软件进行数值模拟，但其未考虑外部载荷的作用，仅仅研究了漂浮式风力机的自由振动分析，结果有较大局限性。由此可见，虽在漂浮式风力机结构被动控制方面取得了诸多成果，但多数研究做了适当的简化，或只考虑单一漂浮式风力机的控制效果。不同漂浮式风力机因其平台结构的不同，动态响应也千差万别，控制效果也存在巨大的差异。

因此，本文选取目前具有代表性的3种漂浮式风力机，在机舱中配置TMD进行控制，研究3种漂浮式风力机在风、浪及流载荷联合作用下的稳定性控制效果，以期为漂浮式风力机的设计和开发提供理论参考。

1 TMD控制时的漂浮式风力机动力学模型

1.1 环境载荷

环境载荷一般为由直接或间接的环境作用所引起的载荷。漂浮式风力机在役于海上，而海洋环境载荷复杂多变，包含风、浪、流、冰及地震等多种因素[15]，为简化计算又不失一般性，本文重点考虑风、浪和流三种主要环境载荷。

1.1.1 风载荷

漂浮式风力机的风载荷主要为风轮和塔架所受气动推力对风力机产生的力矩，如式(1)所示

Fw=Fblade+Ftower

(1)

式中:Fblade为风力机风轮气动推力；Ftower为塔架气动推力。

计算风轮气动载荷时是使用了叶素动量理论结合动态入流方法。采用平均参数、侧向参数及垂直参数描述整个风轮平面上的诱导速度变化规律，其可反映风速变化时，风轮平面上诱导速度的不均匀分布，再结合叶素动量理论求解气动载荷。

风轮平面的诱导速度不均匀分布的一阶傅里叶级数表达式为

λ(r,ψ)=v0+vsμsinψ+vcμcosψ

(2)

式中:v0，vs和vc分别为诱导速度的平均分布、水平分布及垂直分布；μ为半径比；ψ为偏航角。

气动力和诱导速度之间的关系为

(3)

式中:[M]为风轮动态入流质量矩阵，反映了入流动态特性；[V]为质量流量参数矩阵；[L]为入流增益矩阵；CT，CMy，CMz分别为风轮推力系数、偏航系数和俯仰系数。通过求解微分方程(3)得到风轮平面诱导速度场，结合叶素动量理论求解风轮气动力。

风力机风轮气动推力Fblade可基于叶素动量理论结合动态入流理论得出表达式

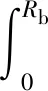
(4)

塔架气动推力Ftower表达式为[16]

(5)

式中:v为风轮高度前的来流风速；ρa为空气密度；Rb为风轮半径；a为风轮处的轴向诱导因子；Ct为阻力系数；D为塔架截面的直径；vh(t)为海平面上塔架高度为h的瞬时风速。

1.1.2 浪载荷

漂浮式风力机所受波浪载荷Fx的表达式为

(6)

漂浮式风力机受波浪载荷Fx作用产生的波浪力矩Mw为

(7)

式中:ρ为海水密度；D为浮体的直径；Cm为附加质量系数；Cd为阻力系数；vx为中点轴线处流体瞬时速度水平分量。

1.1.3 流载荷

在工程设计应用中，通常将海流视为稳定流动，并认为其对漂浮式风力机的作用力为拖曳力，单位高度拖曳力的表达式为

(8)

则作用在整个漂浮式风力机上的作用力为

(9)

式中:ρ为海水密度；Cd为阻力系数；A为结构在与流速垂直平面上的投影面积；vc为海流流速。

1.2 惯性力载荷和重力载荷

作用在风轮上的载荷除气动载荷外，还有惯性力载荷和重力载荷等。在风轮坐标系中，重力拉力、重力剪力及重力弯矩分别为

(10)

(11)

(12)

式中:R为风轮半径；r为叶根距叶轮中心的距离；m为叶片单位长度质量；ω为叶片旋转角；δ为叶片安装角；g为重力加速度。

在轮毂坐标系中，离心力为

(13)

(14)

离心力弯矩及离心力扭矩分别为

(15)

(16)

式中，er为叶根坐标系与轮毂坐标系原点之间的距离。

1.3 TMD耦合动力学模型

在漂浮式风力机机舱中配置了TMD后，漂浮式风力机将在原有的基础上耦合新的自由度，其耦合模型中增加了TMD相关的驱动力和惯性力。故漂浮式风力机和TMD的运动方程为

(17)

kTMDRTMD(RTMDφt-xTMD)-

mTMDg(RTMDφt-xTMD)-

(18)

(19)

式中，Ip，It分别为平台和塔架的转动惯量；φp，φt分别为平台和塔架偏离垂直面的角位移；kp，dp分别为系泊的刚度和阻尼系数；kt，dt分别为塔架的刚度和阻尼系数；RTMD，Rt及Rp分别为TMD结构，塔架及平台的质心到铰接处的距离；FW，Mw及Fc为上文描述的风、浪及流载荷。

2 漂浮式风力机模型、TMD设计及环境参数

2.1 漂浮式风力机模型

本文研究对象为目前具有代表性的3中漂浮式风力机平台：ITI Barge、OC3-Hywind Spar以及OC4-DeepCwind Semi，三种平台均搭载相同的NREL 5MW风力机。风力机[17]及三种平台的主要参数如表1及表2所示。三种平台及风力机构建的整体风力机模型如图1所示，其中风力机仰角为5°，锥角为2.5°，无偏航，采用变桨控制策略，叶片为柔性叶片。

表1 风力机参数Tab.1 Parameters of the wind turbine

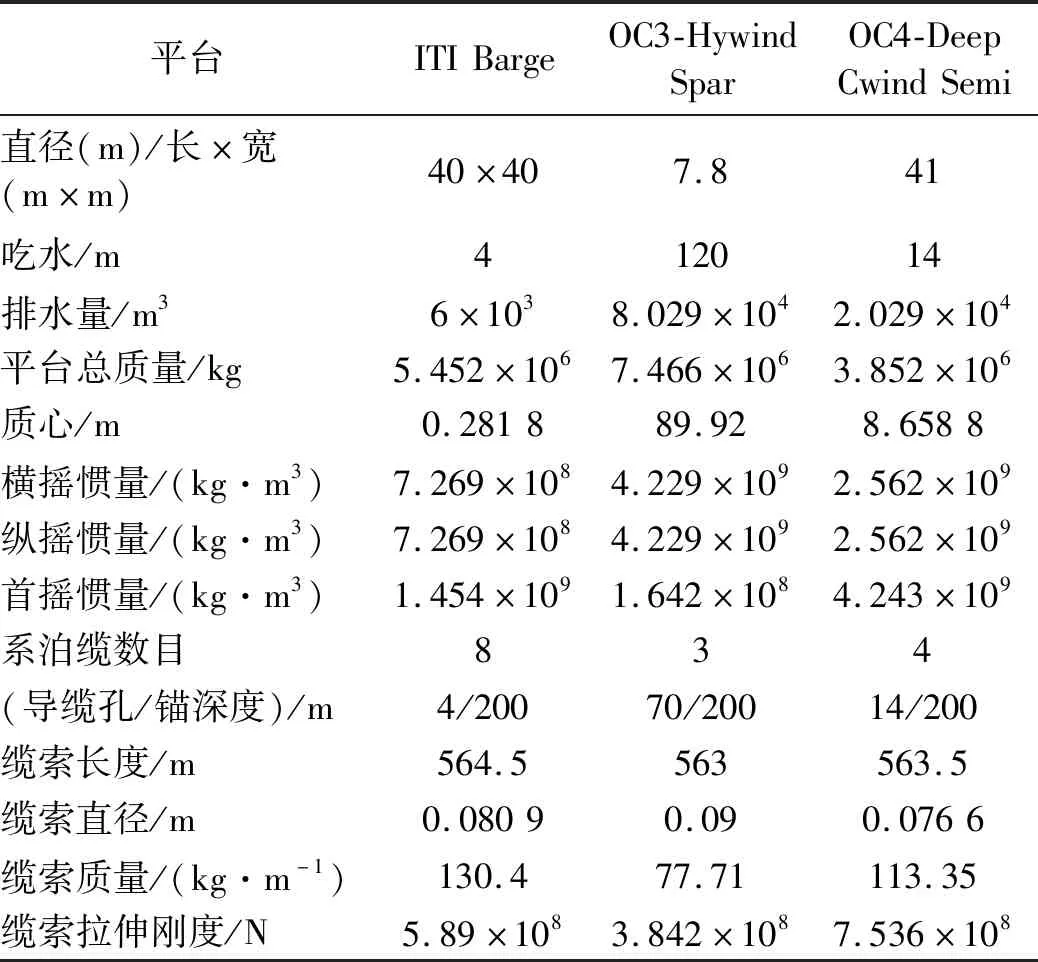
表2 平台参数Tab.2 Parameters of the platforms

2.2 TMD设计

TMD由固体质量块、弹簧减振器、阻尼器以及支撑系统组成。可将其固有频率调谐至接近被减振结构的固有频率或外部激励频率，当主体结构受外部激励作用产生振动时，TMD系统会产生与主体结构振动方向相反的惯性力，同时通过阻尼系统吸收主体结构的振动能量，并将能量耗散，从而达到控制主体结构稳定性的目的[18-19]。为提高控制效果，可将TMD安装在漂浮式风力机机舱处，其模型示意图及控制原理如图2所示。其中H(s)为主体结构的传递函数，G(s)为TMD结构的传递函数，f(t)为主体结构的初动态响应，p(t)为TMD结构的动态响应，x(t)为TMD控制后主体结构的运动响应。

(a)Barge

(b)Spar

(c)Semi图1 漂浮式风力机模型Fig.1 Model of floating wind turbines

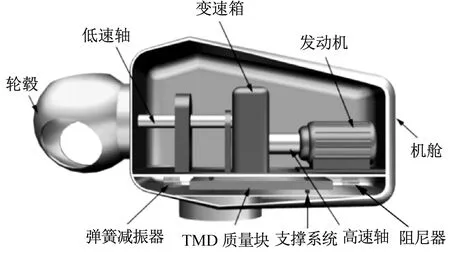
(a)TMD模型示意图

(b)TMD模型原理图图2 漂浮式风力机TMD模型及其控制原理Fig.2 Floating platform of wind turbine TMD model and control principle

可通过调节TMD质量(m)，TMD刚度(k)以及TMD阻尼(d)等参数进行稳定性控制。在传统高耸建筑结构中，TMD的质量占主体结构质量的百分比，即质量比为0.25%～2%。漂浮式风力机相较于一般传统高耸建筑，质量更小且柔性更大，故质量比可取范围内的小值，本文的质量比取值为0.5%。TMD刚度及阻尼可由下式计算

(20)

d=4πfdξdm

(21)

式中:fd为TMD自振频率；m为TMD质量；ξd为阻尼比。

根据上述公式，三种漂浮式风力机的TMD参数如表3所示。

表3 TMD参数Tab.3 Parameters of TMD

2.3 环境参数

为研究TMD对漂浮式风力机稳定性的控制效果，有无TMD控制时的工况都取相同的极限环境参数，如表4所示，其中风载荷参数为使用Trubsim生成的Kaimal风谱，为全域湍流风，同时基于工程上常用的简化指数风廓线公式(乘幂率)刻画风剪切。设定时历平均风速为18 m/s，风力机在处于高于额定风速，小于切出风速之间运行，采用变桨控制策略。低于额定风速时，风力机无需变桨，浆距角为0；随着风速增大，风轮转速逐渐增大，超过额定风速时，风轮转速不变，风力机通过动态变桨策略以维持功率输出不变。

表4 环境参数Tab.4 Parameters of the environment

3 数值计算结果与分析

3.1 无TMD控制时三种漂浮式风力机动态响应对比分析

漂浮式风力机受复杂的环境载荷作用，其最直观的动态响应为平动位移和转动偏转角。其中塔顶位移和平台偏转角对结构疲劳载荷和整机发电效率相关性很大。考虑篇幅原因，现给出三种漂浮式风力机在复杂风、浪和流载荷作用下，塔顶左右位移和平台首摇偏转角对比图，如图3所示。

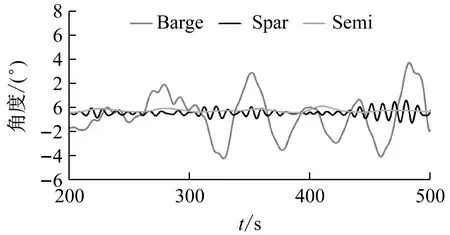
(a)平台首摇角

(b)塔顶左右位移图3 三种漂浮式风力机动态响应时域图Fig.3 Time history of dynamic response of three types floating wind turbines

如图3所示，三种漂浮式风力机在运行一段时间后，动态响应变化均不相同。由图3(a)可知，在平台首摇方向上，Barge平台响应幅度远大于Spar平台和Semi平台；Spar平台与Semi平台响应幅度虽相差不大，但Spar平台响应幅度还是略大于Semi平台。由图3(b)可知，在塔顶左右位移方向上，Barge平台响应幅度同样远大于其他两平台，与平台首摇方向不同的是，Semi平台动态响应大于Spar平台。Barge平台动态响应远大于其他平台的原因是其水线面面积较大及吃水浅，导致其对波浪的砰击作用更为敏感。

3.2 TMD控制时各漂浮式风力机动态响应对比分析

3.2.1 Barge型漂浮式风力机动态响应

Barge型漂浮式风力机在TMD控制下的动态响应如图4所示，其中图4(a)为平台首摇角，图4(b)为塔顶左右位移。

如图4所示，Barge型漂浮式风力机在TMD控制下，动态响应幅度都有所降低。无控制情况下，平台首摇角在-4°～4°之间较规律波动；TMD控制后，平台首摇角的波动降低到-2.6°～1.2°。塔顶左右位移同样得到有效控制，其最大波动范围由-0.36～0.22 m降低到-0.21～0.12 m，减小幅度十分明显。无控制时，Barge型漂浮式风力机的平台首摇角和塔顶左右位移标准差分别为1.82和0.12，TMD控制后，两者的标准差分别为0.84和0.05。计算可知，平台首摇角和塔顶左右位移的稳定性分别显著提升了53.60%和60.30%。

波浪谱密度函数，或称能量谱，可用于表示在不规则波中波浪对平台作用的能量相对于频率的分布。响应谱是波浪密度函数(能量谱)与平台传递函数平方的积。因此，为了更加深入探究TMD对漂浮式风力机的控制效果，通过上述平台首摇角和塔顶左右位移时域图变换得出两者相对应的响应谱，如图5所示。其中横坐标为频率，纵坐标为响应幅值。

(a)平台首摇角

(b)塔顶左右位移图4 Barge型漂浮式风力机动态响应时域图Fig.4 Time history of dynamic response of barge floating wind turbine

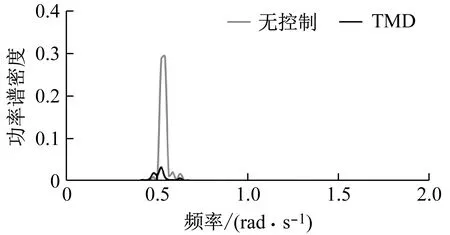
(b)塔顶左右位移图5 Barge型漂浮式风力机响应谱Fig.5 Response spectrum of barge floating wind turbine

由图5可知，在平台首摇方向上，有无TMD控制两种情况的响应都集中在0.04～0.21 rad/s，且都存在双峰；不同的是，无控制时，呈现出高低不同的双峰，而TMD控制时，双峰更加均匀。在塔顶左右位移方向上，两种情况的响应集中范围相同，都在0.42～0.63 rad/s之间，呈现波频响应。TMD控制后，Barge型漂浮式风力机的平台首摇角和塔顶左右位移响应谱峰值分别为55.443和0.293，各自都远小于无控制时的平台首摇角(6.602)和塔顶左右位移响应谱峰值(0.032)，体现了TMD控制后，漂浮式风力机更加优越的波频性能。

综上所述，TMD控制对Barge型漂浮式风力机的平台首摇角和塔顶左右位移都能起到良好的控制作用。

3.2.2 Spar型漂浮式风力机动态响应

TMD控制时，Spar型漂浮式风力机的动态响应如图6所示，其中图6(a)为平台首摇角，图6(b)为塔顶左右位移。

(a)平台首摇角

(b)塔顶左右位移图6 Spar型漂浮式风力机动态响应时域图Fig.6 Time history of dynamic response of spar floating wind turbine

如图6所示，在平台首摇方向上，TMD的控制作用并不是很明显，响应幅度只减小了一点；有无TMD控制时，平台的首摇角标准差分别为0.250和0.277，即其稳定性仅提升了9.75%。在塔顶左右位移方向上，TMD的控制效果比在平台首摇方向上的控制效果好，响应幅度有明显降低；有无TMD控制时，塔顶左右位移标准差分别为0.004 7和0.003 29，其稳定性提升了29.79%。

图7为平台首摇角和塔顶左右位移的响应谱。

由图7可知，在平台首摇方向上，TMD控制时，响应谱峰值相较于无控制时有所下降，但下降幅度很小，其余部分两者的响应谱曲线趋于重合，且响应集中范围相同，都在0.44～0.92 rad/s范围内。在塔顶左右位移方向上，有无TMD控制的响应集中范围相同，在低频率(0.52～1.11 rad/s)和高频率(2.95～3.83 rad/s)都有分布。且TMD控制时，高频率区域的响应谱峰值明显低于无控制时的响应谱峰值。

(a)平台首摇角

(b)塔顶左右位移图7 Spar型漂浮式风力机响应谱Fig.7 Response spectrum of spar floating wind turbine

综上所述，TMD控制对Spar型漂浮式风力机的塔顶左右位移能起到良好的控制作用，但对平台横摇角的控制作用却不太明显。

3.2.3 Semi型漂浮式风力机动态响应

Semi型漂浮式风力机在TMD控制下的动态响应如图8所示，其中图8(a)为平台首摇角，图8(b)为塔顶左右位移。

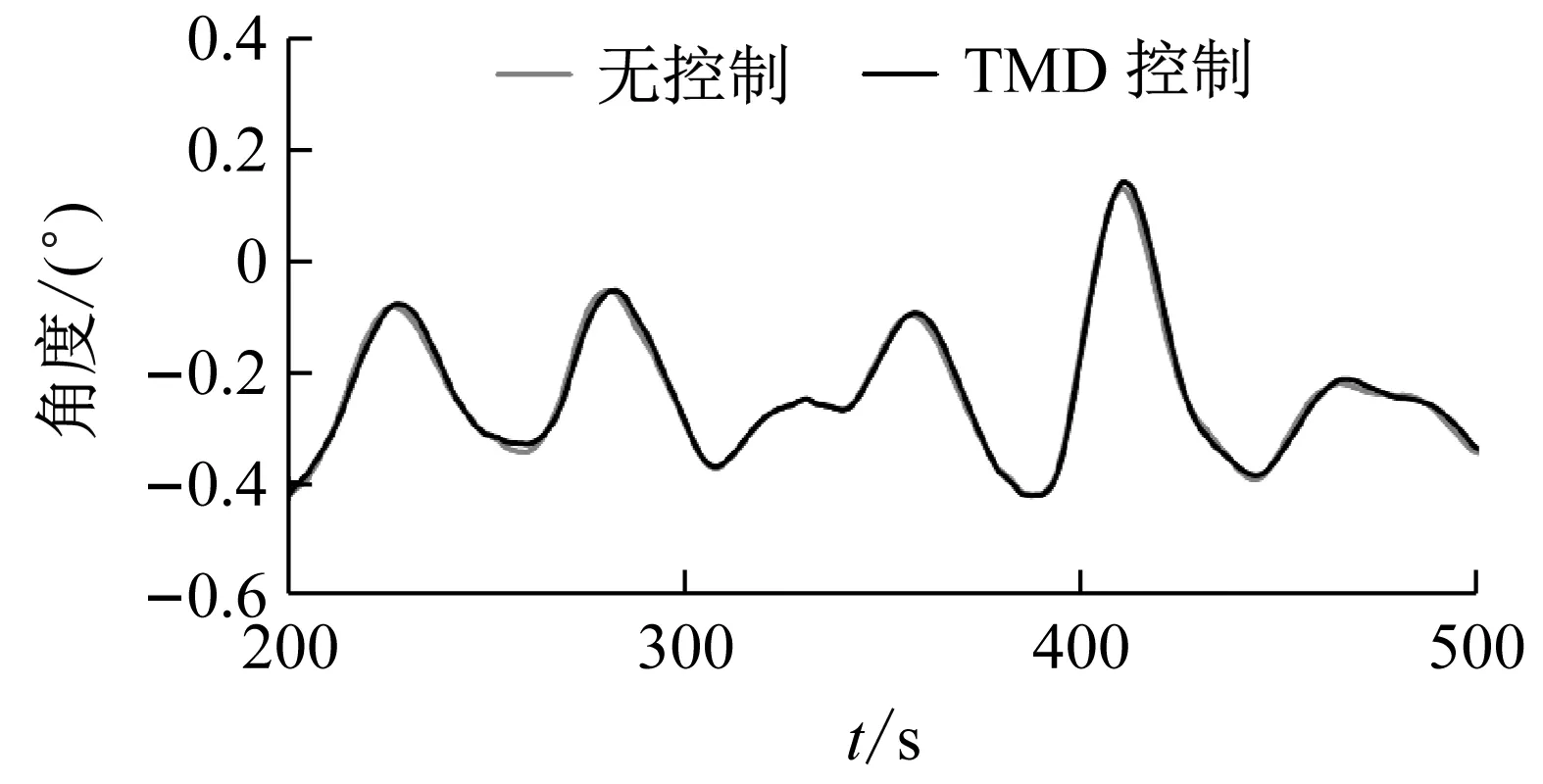
(a)平台首摇角

(b)塔顶左右位移图8 Semi型漂浮式风力机动态响应时域图Fig.8 Time history of dynamic response of semi floating wind turbine

如图8所示，在平台首摇方向上，TMD控制时的平台首摇角时域响应曲线与无控制时的平台首摇角时域响应曲线几乎完全重合；无控制时的平台首摇角标准差为0.118，TMD控制时的平台首摇角标准差为0.119，两者几乎相等；可见TMD的控制作用极其微弱，甚至是没有控制效果。在塔顶左右位移方向上，TMD控制效果有明显好转，无控制时的塔顶左右位移标准差为0.038 8，TMD控制时的塔顶左右位移标准差为0.027 8；即TMD控制时，塔顶左右位移稳定性提升了28.46%。

图9为平台首摇角和塔顶左右位移的响应谱。

(a)平台首摇角

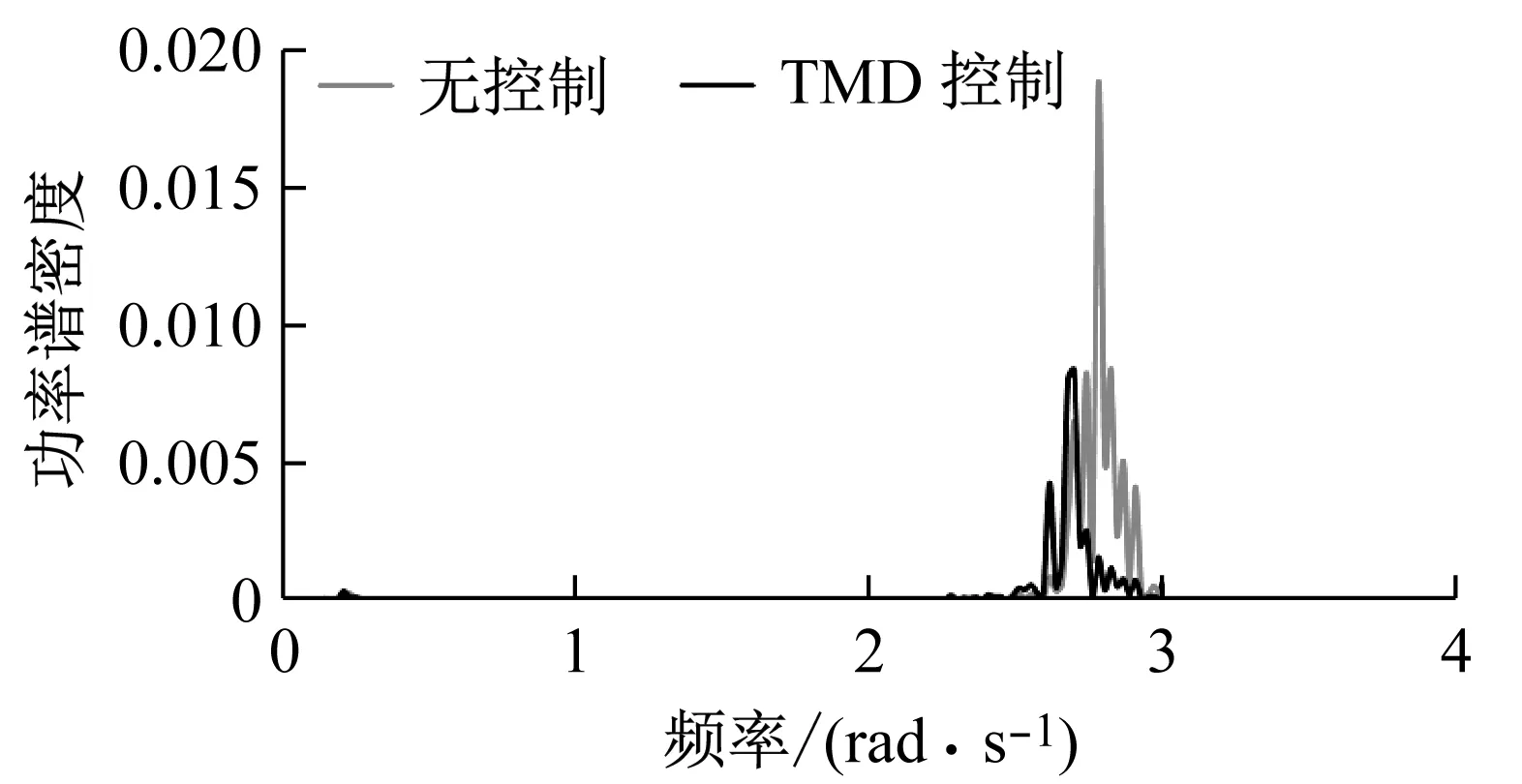
(b)塔顶左右位移图9 Semi型漂浮式风力机响应谱Fig.9 Response spectrum of semi floating wind turbine

由图9可知，在平台首摇方向上，TMD控制时的响应谱曲线与无控制时的响应谱曲线基本重叠，也可说明TMD没起到控制作用。在塔顶左右位移方向上，有无TMD控制的响应谱曲线响应集中在2.41～2.97 rad/s范围内；TMD控制时的响应谱曲线有明显的下降，响应谱峰值由0.018 8降低到0.008 4。

综上所述，TMD控制对Semi型漂浮式风力机的平台首摇角几乎没有控制作用，对塔顶左右位移的控制作用较为明显。

3.3 TMD控制时三种漂浮式风力机动态响应对比分析

图10和图11分别为TMD控制时三种漂浮式风力机平台首摇偏转角和塔顶左右位移对比图，为了更加直观地体现TMD的控制效果，与图3无控制的平台首摇偏转角和塔顶左右位移进行对比。

如图10和图11所示，在平台首摇方向上，TMD控制后，Barge型漂浮式风力机的响应大幅度减小，与Spar型漂浮式风力机的响应接近，但还是大于Semi型漂浮式风力机的响应；在塔顶左右位移方向上，TMD对Barge型漂浮式风力机的控制效果依然很好，响应大幅减小，与Semi型漂浮式风力机的响应接近，大于Spar型漂浮式风力机的响应。分析其原因，三种漂浮式风力机中，Barge型漂浮式风力机优点是结构简单、定位容易、投资少且受水位影响小，但由于吃水浅和水线面面积较大，导致对波浪砰击作用较敏感，动态响应最大，因此受到的控制作用最大，控制效果最好。Spar型漂浮式风力机主体高径比较大，可保持稳定性，动态响应较Barge型漂浮式风力机小，其受控作用也相对较小。Semi型漂浮式风力机甲板空间及甲板载荷可变范围大、抗风浪能力强，动态响应较Spar型漂浮式风力机小，其受控作用也相对较小。

(a)无控制

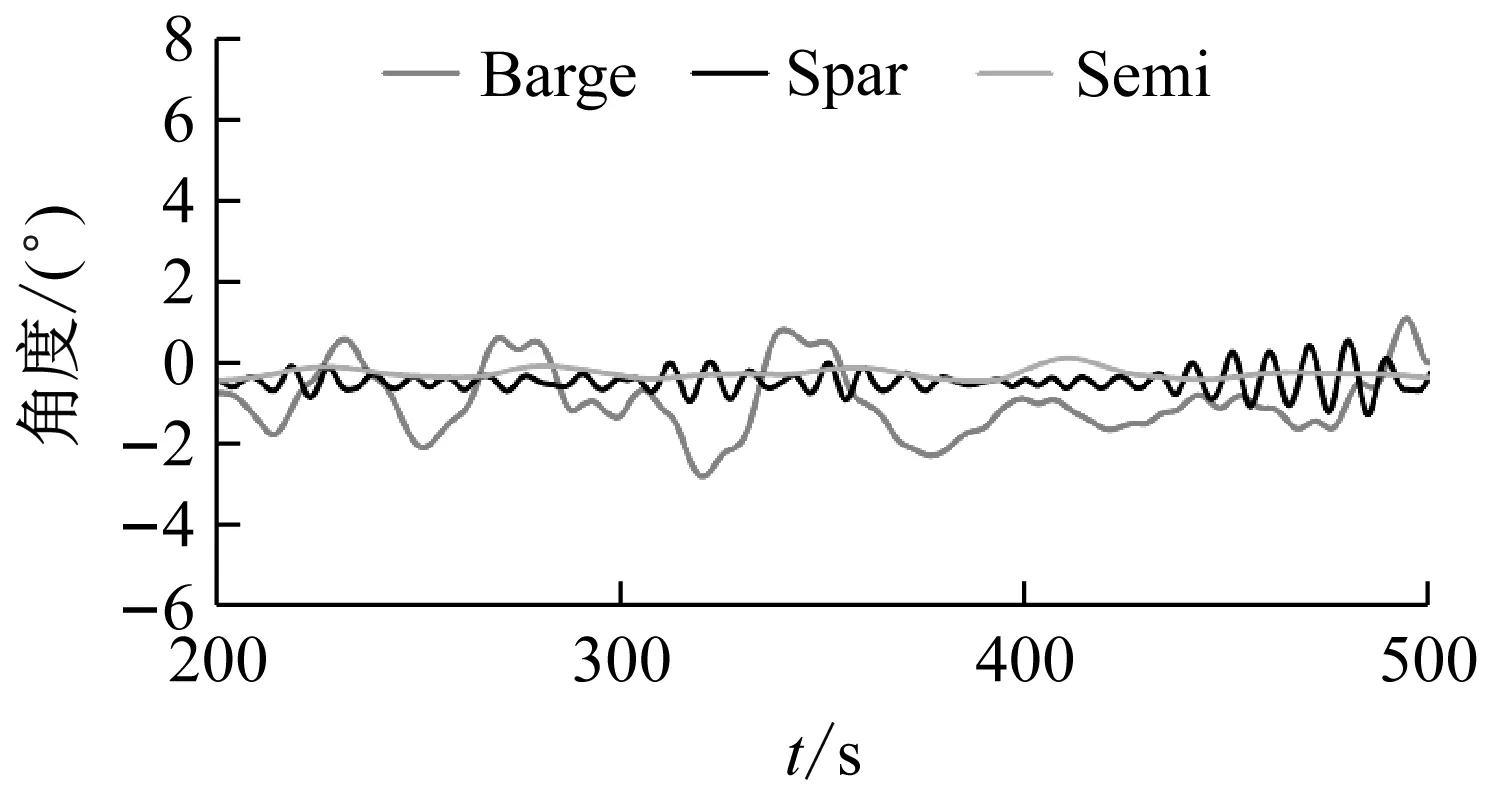
(b)TMD控制图10 平台首摇偏转角Fig.10 Yaw angles of platforms

(a)无控制

(b)TMD控制图11 塔顶左右位移Fig.11 Longitudinal displacements of top of the towers

4 结 论

本文选取目前具有代表性的Barge、Spar和Semi型漂浮式风力机，在机舱中配置TMD系统，考虑漂浮式风力机实际部署海域的海况，对比分析了3种漂浮式风力机在风、浪及流载荷联合作用下的TMD稳定性控制效果，主要结论如下：

(1)无TMD控制时，在平台首摇方向上，Barge平台响应幅度远大于Spar平台和Semi平台，Spar平台响应幅度略大于Semi平台。在塔顶左右位移方向上，Barge平台响应幅度同样远大于其他两平台，Semi平台动态响应大于Spar平台。

(2)TMD控制时，Barge型漂浮式风力机的动态响应幅度都有所降低，且有更加优越的波频性能。平台首摇角和塔顶左右位移的稳定性分别显著提升了53.60%和60.30%。

(3)TMD控制时，Spar型漂浮式风力机的平台的首摇角减小幅度不明显，稳定性仅提升了9.75%；塔顶左右位移的控制效果好，稳定性提升了29.79%。

(4)TMD控制时，Semi型漂浮式风力机的平台首摇角没有控制效果；塔顶左右位移的TMD控制效果有明显好转，稳定性提升了28.46%。

(5)TMD控制时，在平台首摇方向上，Barge型漂浮式风力机的响应大幅度减小，与Spar型漂浮式风力机的响应接近，但还是大于Semi型漂浮式风力机的响应；在塔顶左右位移方向上，Barge型漂浮式风力机与Semi型的响应接近，大于Spar型漂浮式风力机的响应。

(6)Barge型漂浮式风力机受TMD控制的效果最好，其次是Spar型，Semi型控制效果最差。