风力发电机组塔架减振控制策略设计

兰 杰，林 淑，付 斌，岳 伟

(东方电气风电有限公司，四川省 德阳市 618000)

0 引言

风力发电机组塔架是支撑风轮、机舱及其内部组件的结构件，占整机成本的很大比重[1-2]。风机塔架极易发生振动，可以说振动是影响风力发电机组安全运行及寿命的重要因素之一[3]。当风力发电机组在自然风条件下运行时，作用在风力发电机组叶片上的空气动力、惯性力和弹性力等交变载荷会使弹性振动体叶片和塔架产生耦合振动，当外界激振力的频率与系统的固有频率相同时，若该固有频率的模态阻尼较小，系统容易发生共振，共振时将对机组产生较大的应力，导致疲劳增大，缩短整机的使用寿命，若塔架振动幅度过大甚至会导致塔筒倒塌事故[4]。因此，塔架振动的控制对减缓机组振动具有重要意义[5-6]。

风电机组振动是一个复杂的系统问题，目前，已有大量学者对机组振动问题进行研究，如采用调谐质量阻尼器、滚球阻尼器等通过振动台来模拟振动情况，以达到减振效果，但因塔架空间、安装工艺等因素，工程上应用并未普及[7-10]。文献[11-12]安装减振支撑装置来缓解机组振动，但因其实施先于风机制造，减振效果无法保障。此外，也有学者开始尝试应用智能控制策略来减振，如文献[13]采用最优控制原理设计偏航控制器，以实现抑制机组振动的目的。文献[14]设计了一种变桨距滑模控制方法，理论上能在一定程度抑制载荷。文献[15-16]基于控制方法的风机塔架减振研究，通过仿真验证塔架疲劳载荷有所减小，取了一定进展，但并未深入研究如何保障机组稳定余量和降低变桨执行机构疲劳等问题。

基于此，本文提出一种塔架阻尼器反馈控制减振方法，通过增加塔架一阶模态阻尼，以保障机组有足够的稳定裕量，同时保障变桨距执行机构所受疲劳载荷减小，使得机组在额定风速以上发电时，塔架顶部的振动位移减小，进而降低塔底载荷，保障风电机组安全稳定运行，在一定程度上提高了风机寿命。

1 塔架受力分析及模型建立

风力发电机组塔架所受的主要载荷[17]包括：1)风在塔架上产生的轴向推力；2)塔架顶端风轮和机舱对塔架产生的重力；3)塔架本身的重力；4)垂直于塔架方向的风压；5)风速垂直梯度而产生的俯仰力矩，由于风轮比较小，可以忽略，暂时不考虑叶轮偏航时产生的陀螺力矩。

在研究塔架载荷时，塔架顶部和底部均采用通用的规范坐标系如图1、2所示。

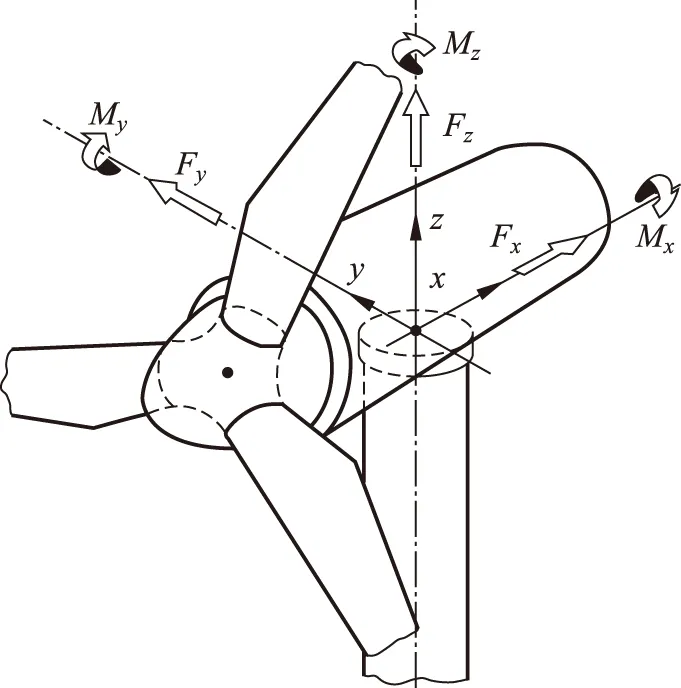
图1 塔架顶部坐标系Fig.1 Coordinate system of tower top

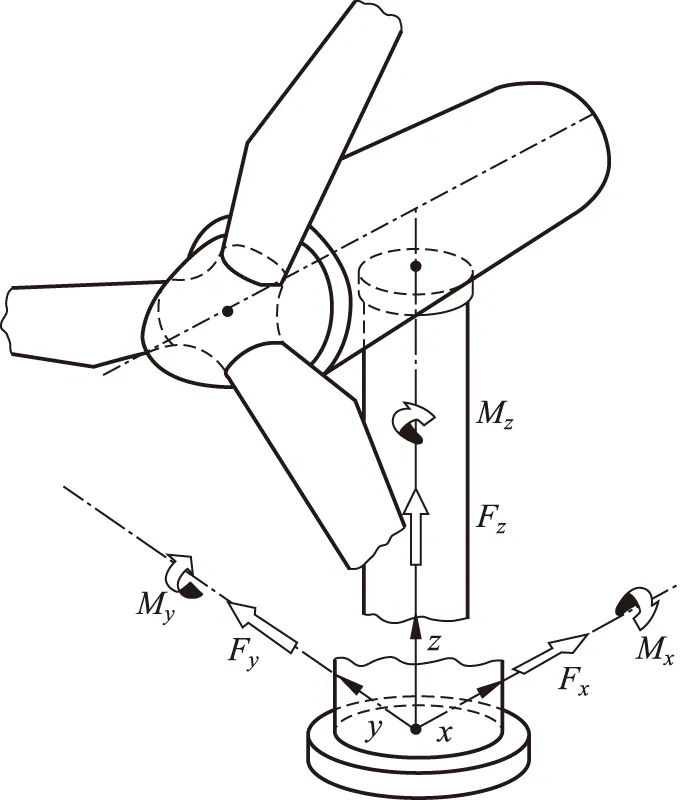
图2 塔架底部坐标系Fig.2 Coordinate system of tower bottom

以钢管式塔架为例，则将其视为一个质量为m、长度为h的悬臂梁，并将风轮和机舱等效为一个质点P，具体如图3所示。

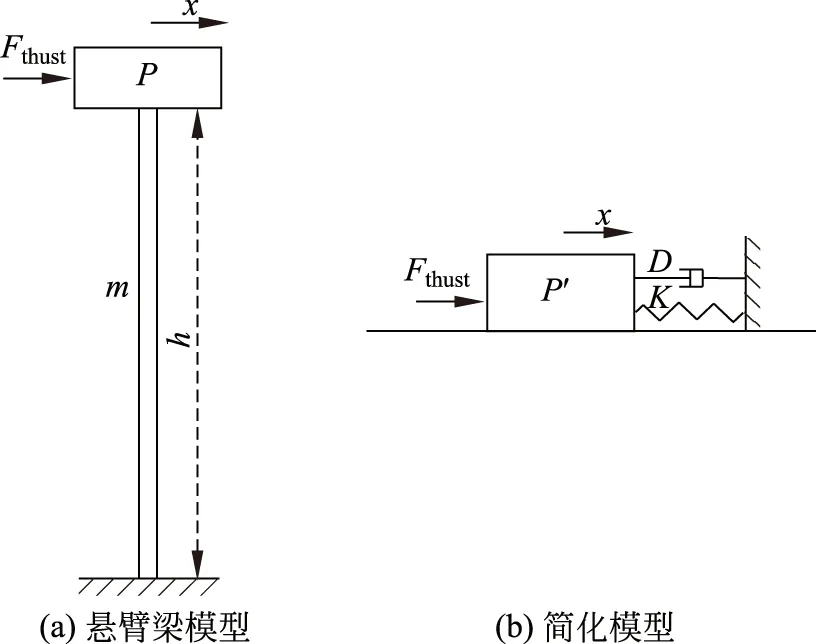
图3 典型的塔架模型Fig.3 Typical tower model

同时不考虑偏航及塔架高阶模态的影响，塔架的动态特性可以用简单的单自由度系统的强迫振动描述：

(1)

式中：M为等价于塔架的模态质量；M′为塔架的等效质量与机舱的等效质量之和，且M′=M+0.23m[18]；K为塔架刚度系数，由振动力学[19]可知K=3EI/h3；D为阻尼项；x为塔架的位移；Fthrust为外加力，即叶轮的推力。

由气动分析知，叶片的桨距角β与风轮受到的推力有紧密关系，典型的推力和桨距角关系曲线如图4所示。

图4 典型的推力和桨距角关系曲线Fig.4 Typical thrust and pitch angle relationship curve

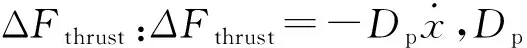
(2)

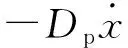
2 塔架振动原因分析

引起塔架振动须包含2个因素：1)激励源，2)相应的模态阻尼较低，由此分析引起塔架振动的主因。

1) 激励源：风电机组塔架振动激励源可分为两类，一类是随机激励，主要是由风速随机变化引起的，由于该类激励的随机性，在设计之初是不能预测的，因此需要考虑从控制角度予以抑制；另一类是固有激励，由风轮旋转引起的，风轮转速引起塔架的激励源主要有2个频率：①风轮旋转频率，此激励主要是质量分布不平衡所致。②风轮旋转频率乘以叶片数目的倍数，如3P，6P等，主要是气动力不平衡所致。

风轮引起塔架耦合振动分析可用坎贝尔(Campbell)图进行分析，风机Campbell图可以反映整机各部件相互耦合之后的模态特性，观察各模态频率在风轮变速运行范围内，是否和P的整数倍等包络线相交，存在交点。若有交点， 则存在风轮-塔架耦合的整机振动问题[20]。图5为某机组的Campbell图，由图5可知，无论是塔架的左右振动模态还是前后振动模态，其阻尼比都非常小，分别为0.592%和6.384%，特别是塔架的左右振动模态，模态阻尼比甚至不到1%，在这种情况下如果塔架受到固定频率的激振力作用，且激振频率刚好等于塔架频率，则极易引起塔架的左右振动。

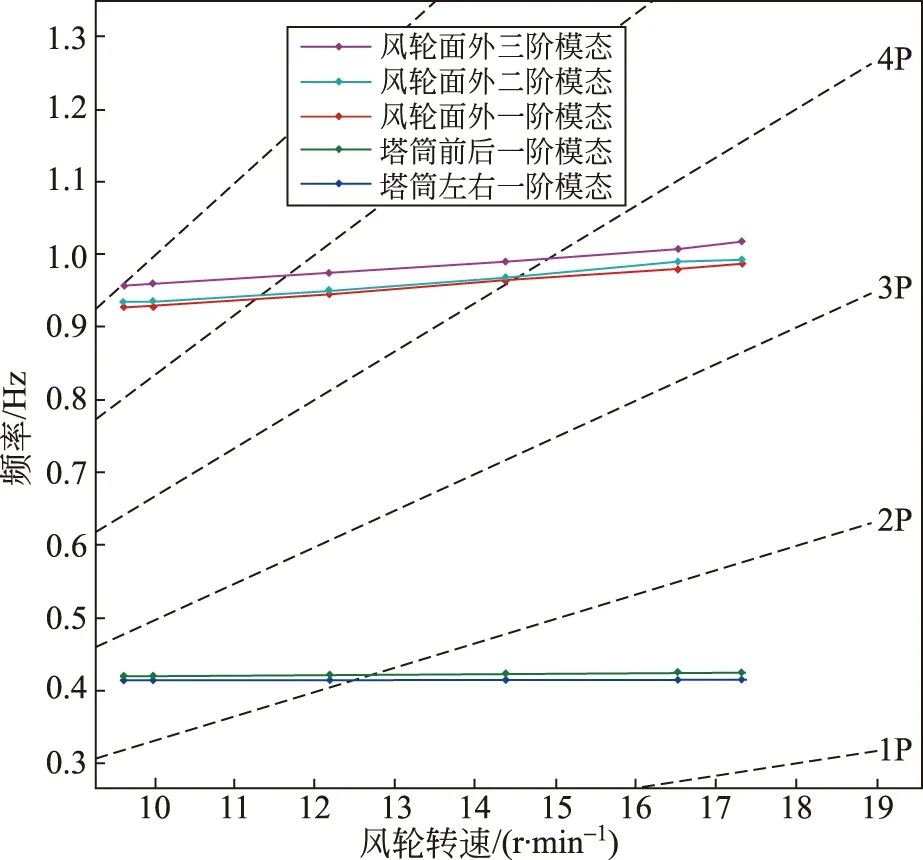
注：塔筒前后一阶模态频率为0.423 13 Hz；塔筒前后一阶模态阻尼比为0.063 841；塔筒左后一阶模态频率为0.415 09 Hz；塔筒左后一阶模态阻尼比为0.005 9227。图5 某机组的Campbell图(塔架部分)Fig.5 Wind turbine Campbell (tower)

值得注意的是：传统的塔架设计以刚性塔架为主，塔架一阶模态频率位于风轮的1倍转频(1P)和3倍转频(3P)之间。然而，随着塔筒设计高度的不断增加，塔架一阶模态频率不断降低。针对柔性塔架的设计则意味着一阶塔架左右、前后固有模态频率和风轮1P穿越频率之间可能存在激振，需要设计转速区域隔离以避免风机运行在塔筒共振转速区域。如图6所示。

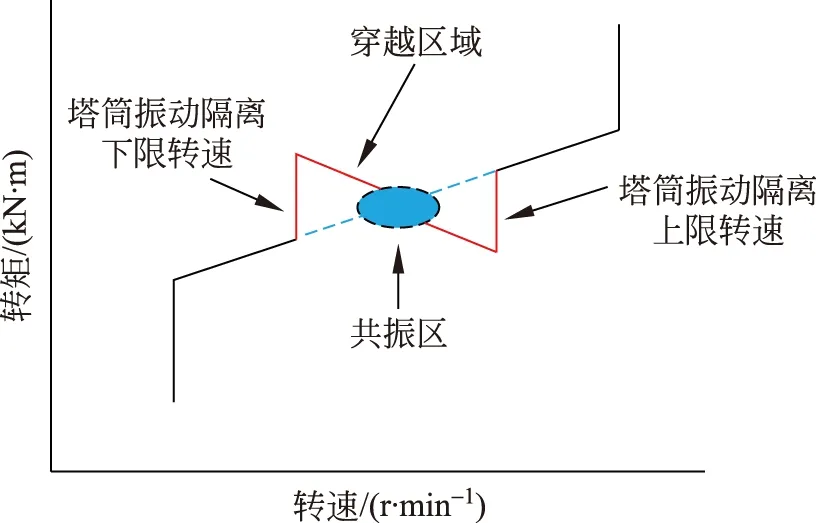
图6 转速转矩控制曲线Fig.6 Speed torque control curve

因此，为避免固有频率之间的耦合干扰，塔架模态频率设计时应尽量避免接近这些已知敏感频率。

2) 模态阻尼：若所对应的模态阻尼较小，在施加对应频率的激励时，就会引起振动，以某国产2 MW风机为例，通过Bladed软件建立风力发电机组模型[21]，并计算其塔架一、二阶模态频率和模态阻尼见表1。

由表1可知，无论是塔架的左右振动模态还是前后振动模态，其阻尼比都非常小，由理论分析可知，其很容易通过相应频率激励引起塔架振动。

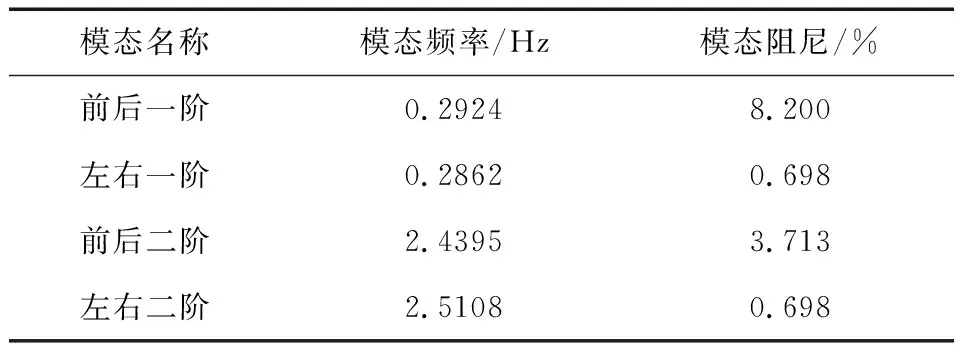
表1 塔架一、二阶模态计算Table 1 Calculation of tower 1st order and 2nd order mode

通过频谱分析可获得典型发电机转速功率谱密度和风速功率谱密度如图7、8所示。

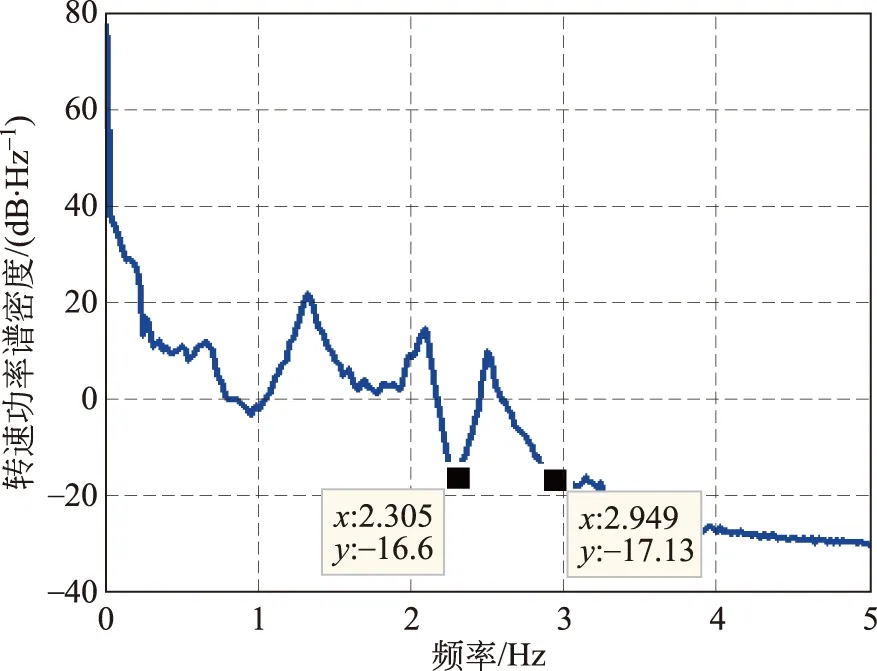
图7 典型发电机转速功率谱密度Fig.7 Typical generator speed power spectral density

由图7所示的转速功率谱可知，转速的主要能量集中在塔架一阶模态附近，二阶模态处的功率密度只占不到1%。由图8所示的随机风速功率谱可知，风速的主要能量也集中在塔架一阶模态附近，因此引起塔架振动主要为一阶模态。

图8 典型湍流风速功率谱密度Fig.8 Typical turbulent wind speed power spectral density

为了减小或降低塔架振动，只要消除引起振动的任意一个因素即可，而通过控制器设计，增加模态阻尼是相对比较容易的方法。

3 塔架阻尼器设计

由控制理论可知，阻尼小的系统超调量大，调节时间长，由表1可知，塔架前后一阶阻尼比为8.2%，属于低阻尼的状态，在风轮推力作用下，会引起顶部的振动位移幅值偏大，塔架疲劳载荷的大幅增加。因此塔架设计时应尽可能增大塔架模态阻尼。

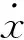
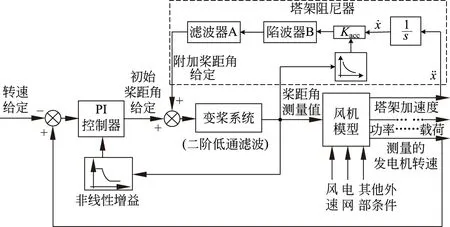
图9 塔架阻尼器反馈控制框图Fig.9 Tower damper feedback control block diagram

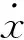
图10 滤波器A特性Fig.10 Characteristics of notch filter A

同时，为避免变桨信号与塔架频率成分耦合在一起激发共振，将桨距角信号中的塔架频率成分(3P、6P等)滤除。二阶陷波器复频域传递函数通用结构如式(5)所示。

(5)

式中：若ω1=ω2且ξ1=0，即为陷波器；如果ξ1>ξ2，为带通陷波器；如果ξ1<ξ2，为带阻陷波器。

通过调节参数，得到如图11所示的频率特性的陷波器B。

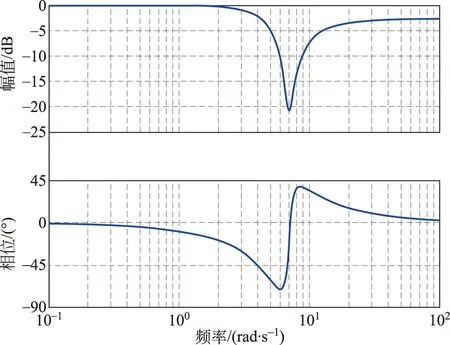
图11 陷波器B特性Fig.11 Characteristics of notch filter B

4 仿真结果

以某国产2 MW风电机组为例，加入塔架阻尼后，通过Matlab仿真分析，得到图12、13所示的从风速给定到塔架顶部振动速度之间的Bode图和变桨控制环节稳定裕量图。

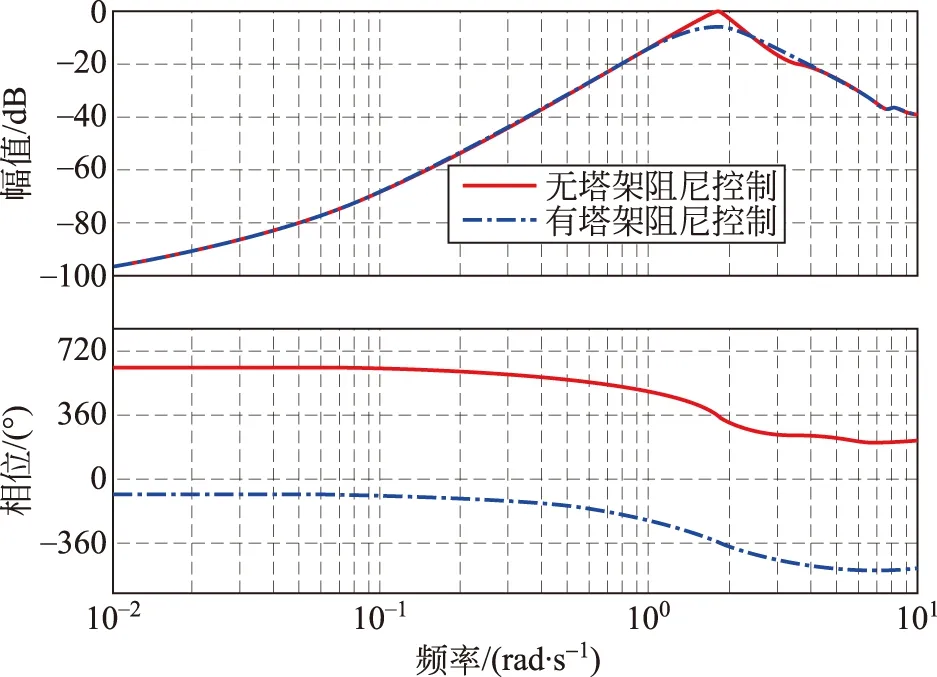
图12 有无塔架阻尼控制的Bode图Fig.12 Bode diagram with or without tower damping control

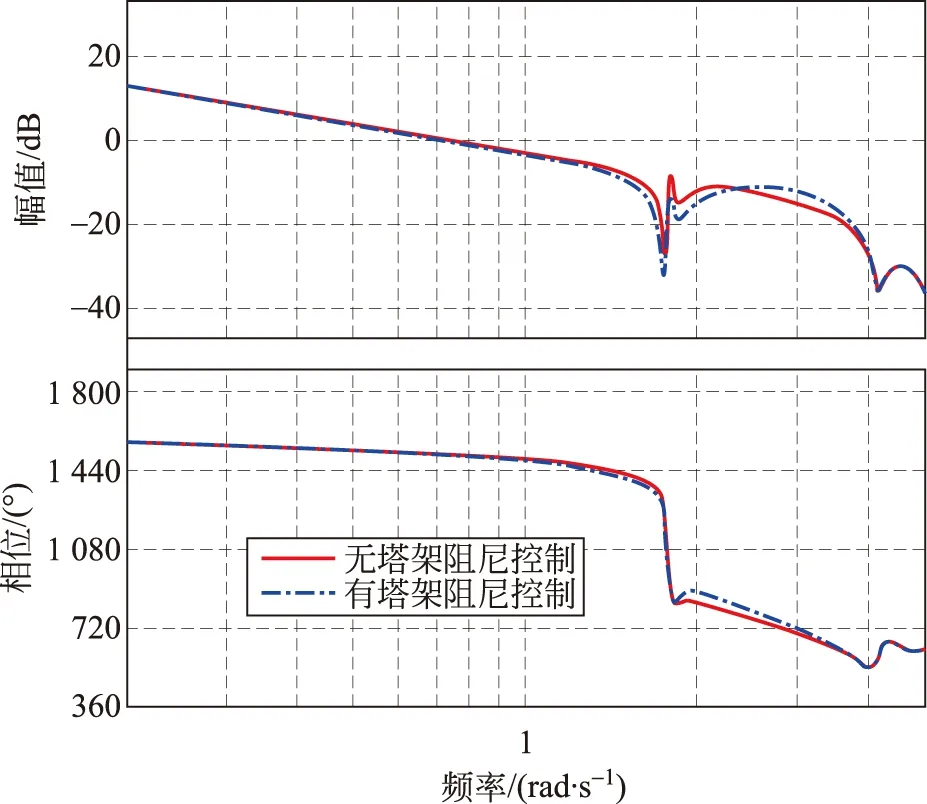
图13 变桨控制环节稳定裕量Fig.13 Stability margin of pitch control link

由图12、13可知：加入塔架阻尼控制后，机舱顶部的振动速度幅值有所减小，即塔架阻尼起到作用，同时塔架加阻控制后，系统具备足够的稳定裕量。

在单位阶跃给定下，风机桨距角时域响应曲线如图14所示。图15为塔架顶部振动加速度的响应曲线。

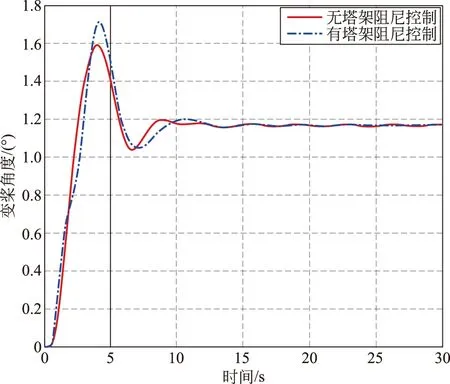
图14 桨距角在单位阶跃风速下的响应Fig.14 The response of pitch angle at unit step wind speed

图15 有无塔架阻尼控制的时域响应Fig.15 Time domain response with or without tower damping control

由图14、15可知：系统在加阻控制后，在单位阶跃作用下，桨距角的单位阶跃响应超调量有所增加，塔架顶部振动加速度的响应幅值有所减小，而且响应比之前衰减的更快，表明塔架阻尼确实有所增加(增加到27%)，即塔架加阻效果良好。

由于塔架的振动主要体现在额定风速以上，根据IEC-61400-1标准进行仿真，风机转速、风机桨距角、风机功率仿真结果见图16—18。

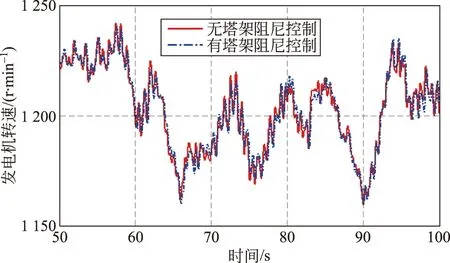
图16 风机转速仿真结果对比Fig.16 Comparison of simulation results of wind speed

由图16、18可知，风轮转速和发电机功率并没有因阻尼控制设计而有较大差别，说明该策略的加入没有对整体控制造成影响。值得注意的是，从图17可以看出，施加阻尼后桨距角的变动不是那么频繁，相对平稳，变桨距执行机构受到的疲劳载荷小，使用寿命更长。

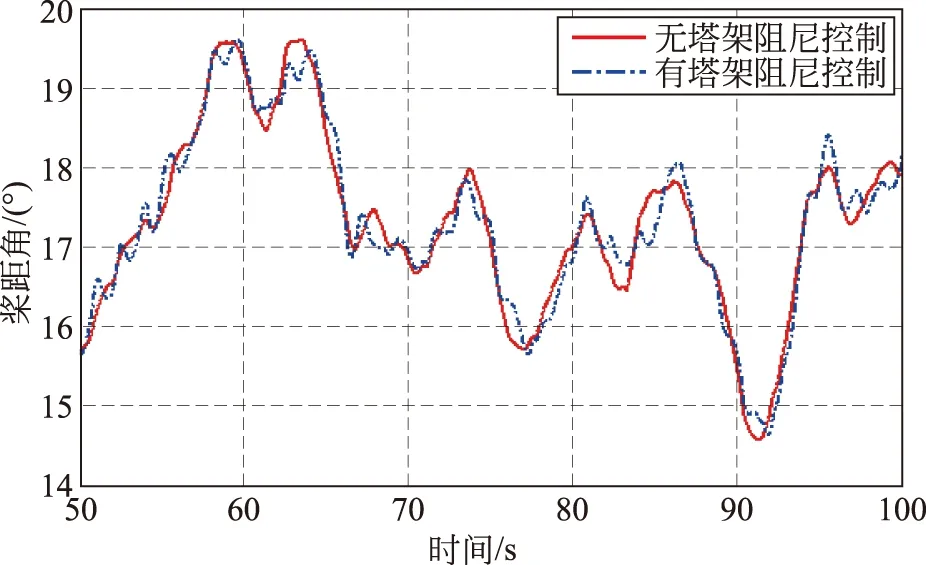
图17 风机桨距角仿真结果对比Fig.17 Comparison of simulation results of pitch angle

进一步对比塔架顶部x方向和y方向的振动位移如图19、20所示。

由图19、20仿真对比可知，在加入塔架阻尼之后，塔架顶部x方向和y方向的振动位移明显变小，很好地减小了塔架的振动，控制效果明显。

图18 风机功率仿真结果对比Fig.18 Comparison of wind turbine power simulation results

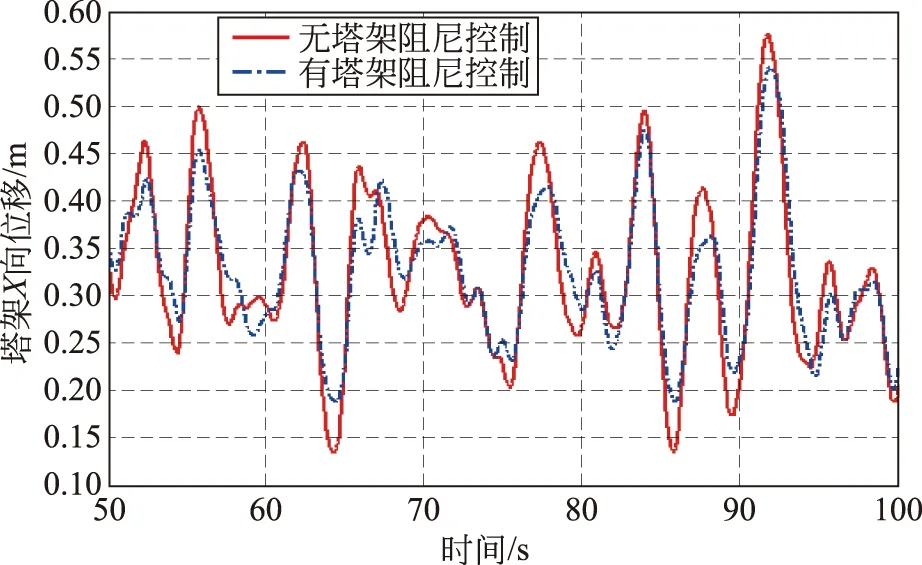
图19 x方向位移仿真结果对比Fig.19 Comparison of simulation results of displacement in the x direction

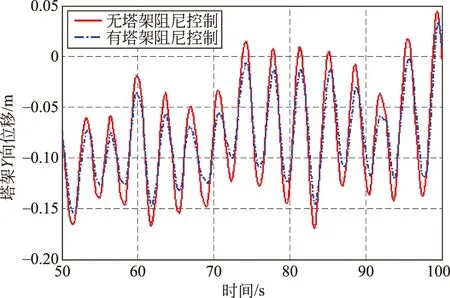
图20 y方向位移仿真结果对比Fig.20 Comparison of simulation results of displacement in the y direction

同时对风机进行发电情况下的仿真，得到塔架底部Fxy、Mxy受力情况的对比曲线如图21、22所示。

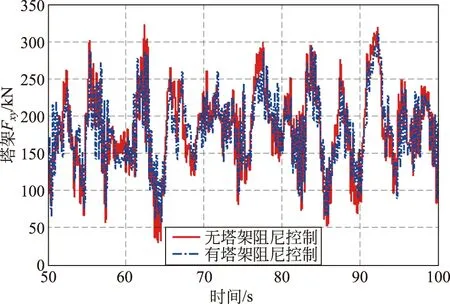
图21 塔架Fxy仿真结果对比Fig.21 Comparison of Fxy simulation results of tower

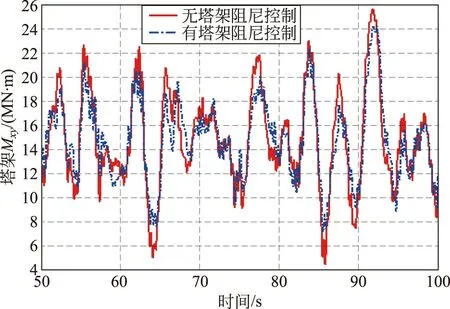
图22 塔架MXY仿真结果对比Fig.22 Comparison of MXY simulation results of tower

由图21、22可知，塔架底部受力情况在加入阻尼控制之后有了明显的改善，有效地保障了风机使用寿命。

5 结论

本文对塔架受力、模型、振动原因进行了分析，并设计了塔架阻尼器反馈控制策略。通过仿真验证，证明此策略能够增加塔架一阶振动模态的阻尼，针对额定风速以上风机发电状态，塔架顶部的振动位移明显减小，塔底载荷有效降低，有效地保障了风机稳定运行，在一定程度上提高了风机寿命。