基于EKF-LESO级联观测的永磁直线同步电机无传感器线性自抗扰控制

董家臣,高钦和,陈志翔，牛海龙

(火箭军工程大学 兵器发射理论与技术国家重点实验室，西安 710025)

“零传动环节”是永磁直线同步电机异于旋转电机的突出结构特点，在赋予电机高推力电流比、高定位精度、高传动效率等优势的同时，也因对扰动的过分敏感而为高精度伺服系统的设计带来困难。电机伺服系统要取得良好的控制效果，依赖于反馈的动子状态信号的品质。目前其位置检测多采用光栅尺、磁栅尺等，这些机械传感器反馈回的状态信息不可避免地受到了噪声的污染，在响应速度要求较高的场合下极易诱发直线电机抖振的产生。与此同时，传感器对环境的温、湿度要求较为苛刻，其使用不仅会增加电机的设计成本和维护成本，还会改变气隙宽度，干扰电机的电感和磁场分布、降低系统的平稳性和可靠性。因此，寻求合适的状态估计算法，实现PMLSM的无传感器控制成为当前研究的热点[1-2]。

直线电机的动子与定子间气隙较大，交直轴电感近似相等，基于凸极效应的高频信号注入法并不适用，基于定子磁链的反电势估算技术成为当前的主流研究方向。孔龙涛等[3]将模型参考自适应法(Model Reference Adaptive System,MRAS)应用在模块化磁通切换永磁直线电机的位置估算中，获得了良好的实验控制效果，但该方法对系统数学模型的准确性要求较高；Wang等[4]应用滑模观测器(Sliding Model Observer,SMO)+锁相环(Phase Locked Loop,PLL)设计了电机的速度估算回路，并引入自适应滤波器减小SMO的抖振以及磁场谐波影响，最终获得了出色的运行平稳度和控制精度，但整个系统设计复杂，对硬件要求很高；韦文祥等[5]使用ESO辨识转子磁链，进而结合MRAS估算转速，明显优点在于消除了纯积分环节的影响，对低速区仍有较高的转速辨识精度，但几种控制方法叠加嵌套使得系统响应较慢。作为基于最小方差估计理论发展起来的一种算法，扩展卡尔曼滤波能有效权衡系统噪声和测量噪声、甚至模型参数不确定度在内的干扰，实现对系统状态的有效估计。将EKF应用于电机运行状态的估算中，获得的估计值较真实值能够具有更少的噪声引入，反馈的信号更平滑[6-7]，有利于减轻控制率突变带来的系统抖振，提高反馈控制系统的平稳性。

电机在运行中，电气信号的品质对电机状态的估算亦存在较大影响，寻求合适的控制策略对伺服系统平稳控制效果的获取同样至关重要。PMLSM在实际运行中，负载变化、推力波动、磁场畸变等均会对动子的运行状态产生影响，这些扰动的随机性、非线性特征较强，对其建模极为困难，使得诸多基于模型的控制策略无法适用。中科院韩京清教授提出的自抗扰控制(Active Disturbance Rejection Control,ADRC)[8-11]是一种不依赖扰动模型的实用控制技术，在继承PID“基于误差消除误差”反馈思想的同时，通过设计扩张状态观测器(Extended State Observer,ESO)实时观测“总扰”，并对控制量进行反馈补偿，可以对包括系统内扰和外扰在内的“总扰”项实施更为高效的抑制，从而大大增强系统的稳定性和鲁棒性。Gao[12]基于带宽思想进一步将ADRC以线性形式实现，大大减小了参数整定的难度，使得线性自抗扰控制(LADRC)具备了广泛工程应用的可能[13-16]。在控制系统的构建中，线性ESO是LADRC的重要组件之一，用于为控制器提供反馈量，但实际上同样有着出色的信息提取能力，通过整定观测带宽能够以较高精度观测系统的各阶状态。

因此，为实现PMLSM的平稳运行,同时摆脱速度传感器的限制，本文提出了一种基于LESO与EKF级联观测的永磁直线同步电机无传感器线性自抗扰控制策略。首先对LESO的观测误差进行理论分析，得出在输入量测信号存在慢时变偏差的情况下，LESO具有从中提取“中阶状态”(2～n)信息的能力，具有一定的容错性。进而以此为依据，提出了EKF+LESO的级联观测方式，搭建了无传感器线性自抗扰控制系统。最后设计仿真和实验，对LESO的容错能力、系统对不同期望输入的跟随能力、整个系统的抗扰能力以及在环境噪声存在的情况下，系统的运行平稳性进行了验证。

1 PMLSM的线性自抗扰控制

1.1 PMLSM建模

永磁直线同步电机由旋转电机演化而来，将旋转电机沿径向剖开、展平，即得到直线电机的基本结构雏形，如图1所示。

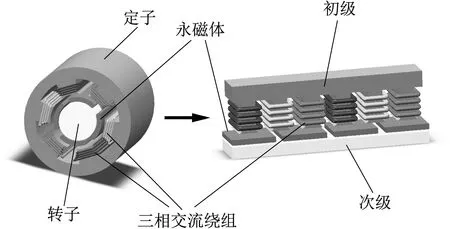
图1 PMLSM的结构演化Fig.1 Structural change from PMSM to PMLSM

结构的相通性使得可以使用旋转电机的模型分析理论来对直线电机进行类比建模。由于电机初、次级之间气隙较大，在d-q坐标系下通常将电感值做Ld=Lq=L处理。在不考虑齿槽效应、磁路饱和、铁心损耗、推力波动、磁场空间谐波等次要因素，且反电势为正弦波、转子无阻尼绕组的情况下，PMLSM在转子d-q坐标系下的电压方程可以表述为

(1)

电磁转矩方程为

(2)

运动方程可由牛顿第二定律给出

(3)

式中：iq为定子绕组的q轴电流；Ψf为永磁体磁链，Te、Tl为电磁转矩、负载转矩；B为黏滞摩擦因数；ω为动子等效到旋转坐标系下的电角速度，ω=πυ/τ，υ为动子速度、τ为极距(同样，后文提到的θ为等效电角度)；J为动子等效转动惯量，np为极对数。

联立式(2)、(3)，并考虑实际建模误差，可得到PMLSM伺服系统的位置环运动方程

(4)

这里，Δw表征简化处理带来的系统未建模部分以及建模不准确部分。

1.2 LADRC系统设计

(5)

按照经典ADRC中忽略h的构建原则，建立LESO如下

(6)

将结果整理成矩阵形式

(7)

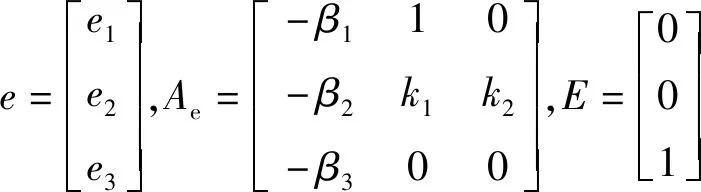
式(7)的特征方程为

λ(s)=λ3+(β1-k1)λ2+(β2-k1β1)λ+k2β3

(8)

依据Lyapunov第一稳定判据，为保证系统的观测稳定性，特征值应全部位于左半平面。同时，为便于参数调节，结合文献[12]基于带宽思想的参数整定方法，将式(8)配成λ(s)=(λ+wo)3的理想形式(wo为设置的观测器的带宽)，得到观测器增益

(9)

考虑按如下形式设计反馈补偿环节

(10)

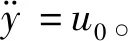
(11)

这样，在频域内将等效后的积分器串联标准模型与控制器模型联立

(12)

可以解出线性状态误差反馈控制率(LSEF)为

(13)

至此，式(6)、(9)、(10)、(13)即构成LADRC系统的主体。其原理图如图2所示。

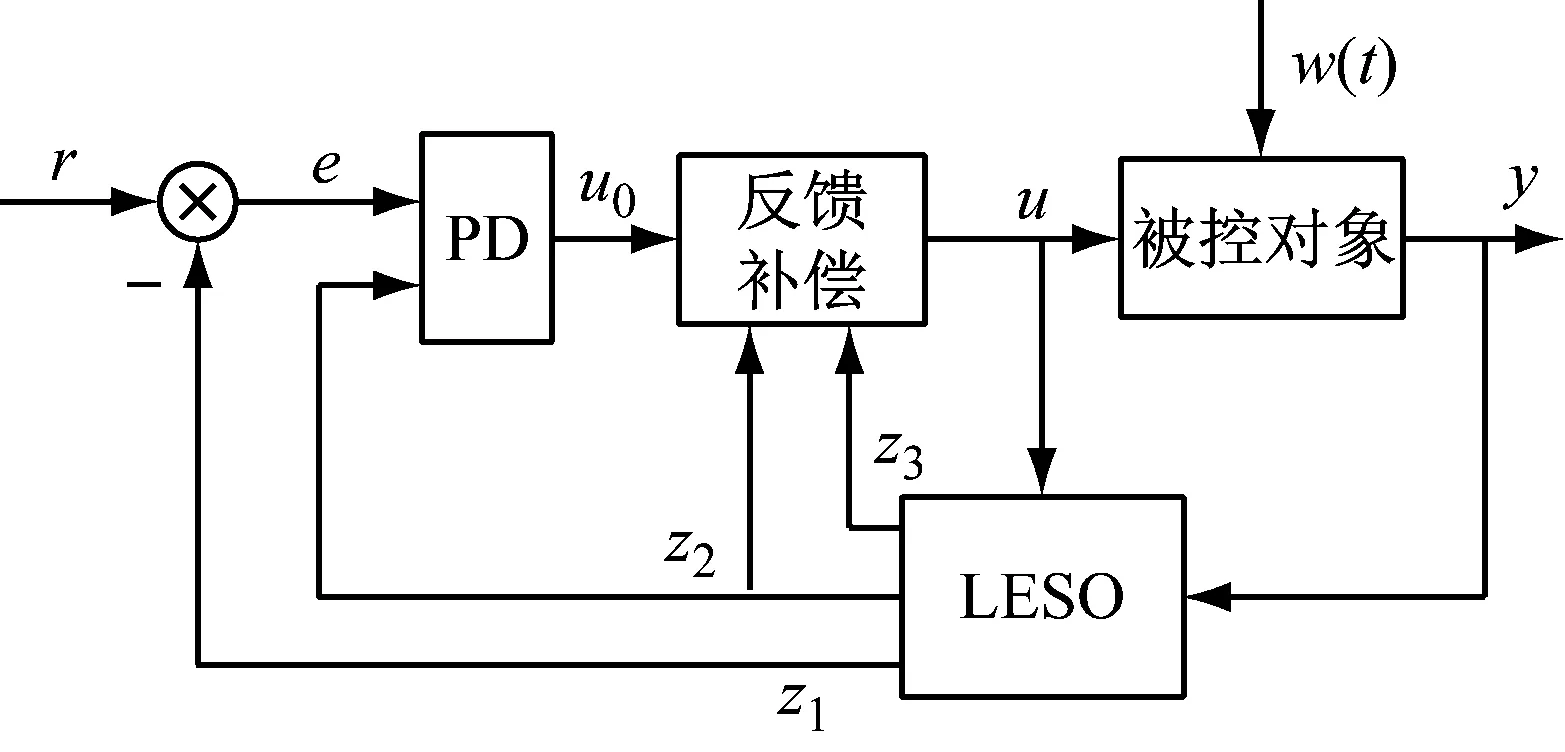
图2 LADRC结构示意图Fig.2 A common LADRC scenario

2 LESO的容错性讨论

扩张状态观测器是自抗扰控制的核心部件，通过对系统各阶状态准确、迅速地观测，为整个闭环系统的控制提供反馈量。目前的文献对其收敛性、观测误差有界性、滤波能力做出了较多研究[17-19]，但对其从输入量中提取状态信息的能力鲜有讨论。为此，本节主要讨论在输入LESO的量测信号存在慢时变偏差的情况下观测器的容错能力。

2.1 LESO的观测精度分析

闭环反馈系统的控制量以PD形式输出，这种控制无静差的前提是LESO有足够的观测精度使被控对象可等效为积分串联标准型；同时总扰项的反馈补偿环节也依赖于LESO。因此，LESO的观测能力直接决定了LADRC系统的控制精度。观测值与PMLSM状态真值之间的偏差主要由两部分构成：

2.1.1 结构误差

与此同时，LESO的扩张状态采取了忽略扰动模型的处理方式，摆脱了对系统的依赖性的同时也使得误差系统引入了Eh项，式(7)的结构形式是非齐次的，因此观测必然存在稳态误差，且其大小与扰动的变化成正比。

2.1.2 量测误差

无传感器控制将动子位置信息的获取由传感器变更为位置估算，算法通过处理实时测得的电气信号换算出θ值，受运行噪声、算法性能的影响，输入LESO的y会存在一定偏差，从而对LESO的观测准确性产生影响。

针对上述误差，在系统运行平稳性能得到保证的前提下，尽可能增大观测器带宽wo可以获得更快的观测速度和更高的观测精度，而选择高性能的无传感器估计算法是减小量测误差的有效办法。

2.2 LESO的容错能力分析

不失一般性，考虑一类SISO(Single-Input-Single- Output)的n阶时变系统

(14)

式中：w(t)为与时间有关的未知外界扰动，其微分项h(t)存在且有界；u为系统的控制输入；y为系统输出；b为控制增益。

考虑输入量存在慢时变偏差对系统各阶状态的观测带来的影响，此时y1=x1+Δθ(t)

按照1.2节思路设计LESO，同样可以获得n+1阶误差矩阵方程

(15)

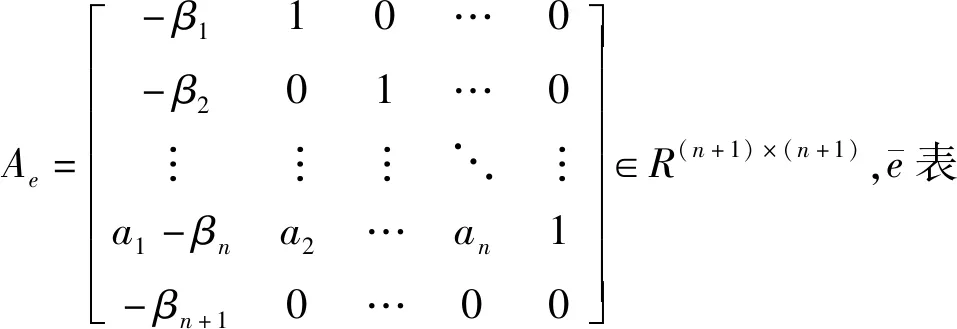
(16)

(17)

该方程在形式上与模型(7)是一致的，带宽wo使其特征方程同样满足Lyapunov第一稳定条件。为进一步简化分析，做如下假设

假设2Δθ(t)有界且为慢时变增量，在LESO的单次观测中可视为恒值Δθ。

假设1、2本质上是不考虑误差的动态收敛过程，这样在步长Δt内的单次观测中，有

AeΔe+LΔθ=0

(18)

将该n+1阶矩阵方程展开、联立，可解出观测精度的稳态耗损量最终表达式

(19)

可见，虽然在结构上LESO对各阶状态的观测均依赖e1趋于0的收敛，但当e1中含有慢时变偏差Δθ时，观测器对第2～n阶的状态观测并不受影响，其观测精度仍然不变。

结论LESO具有一定的容错性，在输入量测信号存在慢时变偏差时，仍能对中阶(2～n)状态实现有效的观测，且观测精度不受这种偏差的影响。

3 无速度传感器算法的实现

3.1 基于EKF算法的动子位置估算

EKF算法以最小均方差原理为基础，通过每一步递推在估算变量的同时实现系统噪声、量测噪声协方差矩阵的实时更新，因而具有出色的环境适应能力和噪声抑制能力。过去由于算法计算量大而限制了其应用范围，但如今处理器芯片的计算能力已经能满足其需求。因此，本文选择EKF作为PMLSM动子位置信号的估计算法。

PMLSM在αβ坐标系下的电压方程可以表述为

(20)

从而将模型(22)扩展为如下矩阵形式

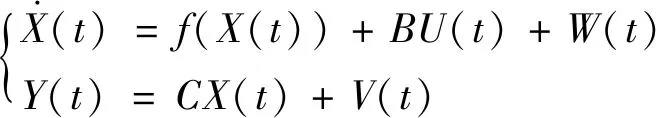
(21)

W、V为0均值，方差矩阵分别为Q、R的高斯噪声，代表系统状态转移噪声向量和测量噪声向量，与X不相关。初始状态向量为具有均值X0、方差P0的高斯随机向量。比对模型(22)，可得非线性项

(22)

对式(24)做一阶泰勒展开可得雅克比矩阵

(23)

系统离散化(h为步长)，可得

(24)

基本离散型EKF状态估计算法如表1所示。

表1 EKF算法Tab.1 EKF algorithm

3.2 级联观测系统设计

EKF算法使用电机的定子电压和电流估算速度和位置信息，考虑运行噪声时变、磁场畸变干扰、初始位置估算不准引入偏差等影响，在设定先验噪声矩阵时通常取较大值，此时转速的估计精度会下降。在长时间运行过程中，电压、电流传感器等电子元器件的老化、积分器零漂引入的直流偏差也是导致估算的电机状态信息不准确的重要原因。

采用合适的控制策略能够抑制系统内部的扰动，从而可以在一定程度上提高EKF对系统状态的估计精度[20-22]。与此同时，第二节中分析了LESO的容错性，因此可以与其他变量估计算法进行串联，以从含偏差的估计量中提取“中阶状态”信息。因此，本文选择抗扰性能出色的LADRC作为PMLSM的控制策略，在速度辨识上，选用LESO+EKF的级联观测方式。由于观测带宽既影响LESO的观测精度，又决定着LADRC系统的控制精度，因而通过整定wo，在获得高精度速度信息的同时，也能提高伺服系统的控制精度。

对PMLSM的电流环，将式(1)变形为

(25)

可见，如果设计udeq、uqeq为控制量，电压模型将不存在耦合，此时非线性环节ωLiq、-(ωLid+ωΨf)需作为前馈补偿项等效进控制量中，进而可以将模型转化为线性系统进行控制。

基于id=0的矢量控制策略，选择应用较广的PI控制构建电流内环伺服回路，在反馈量的选择上，补偿项的转速反馈量应选取LESO的估计值。由于LESO对输入量y=x1没有校正能力，且EKF滤波效果较好，动子位置应以EKF估计值为准。LESO在电机状态的级联观测中承担校正转速估值的作用，同时在整个LADRC系统中作为总扰项的反馈源，为控制量提供反馈信息。

最终设计的无传感器控制系统如图3所示。

4 仿真及实验

为验证本文所提出的级联观测系统的可行，在Matlab2015b/Simulink环境下按图3搭建了仿真系统，针对LESO的容错能力、系统对不同期望输入的跟随能力、整个系统的抗扰能力进行仿真验证。进而基于DSP28335的PMLSM控制平台，通过实验进一步验证真实环境下(电机模型含不缺定度、系统存在噪声)级联观测的有效性以及直线电机无传感器线性自抗扰控制系统的运行平稳性。

4.1 仿 真

仿真模型建立在第一节中的等效旋转坐标系下，参数设置如表2所示。

4.1.1 LESO的容错性验证

在转速辨识的仿真中，设定期望转子信号为单位幅值、频率为15 Hz的正弦信号，在EKF辨识出的转子位置信号输入LESO的过程中人为加载恒值偏差(y，观察系统的级联观测情况。图4的仿真结果表明，设计的无传感器LADRC系统能够正常运行，由图4(a)可见，在对转子位置信号的估计上，EKF算法存在一定的观测滞后，这是数字滤波器无法避免的缺点，级联的LESO只是跟随EKF的估计值，并不产生修正作用，因此整个系统的估计精度由EKF决定。由图4(b)则明显看出，在对“中阶状态”——转速的估计上，LESO从转角中提取出的转速要明显优于EKF对转速的直接估计值，同时相位滞后大大减轻，对转速的跟踪精度得到近十倍的提高。

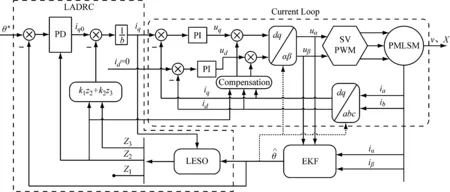
图3 基于EKF-LESO级联观测的LADRC系统设计图Fig.3 The sensorless LADRC system with EKF-LESO

表2 仿真参数Tab.2 Simulation parameters

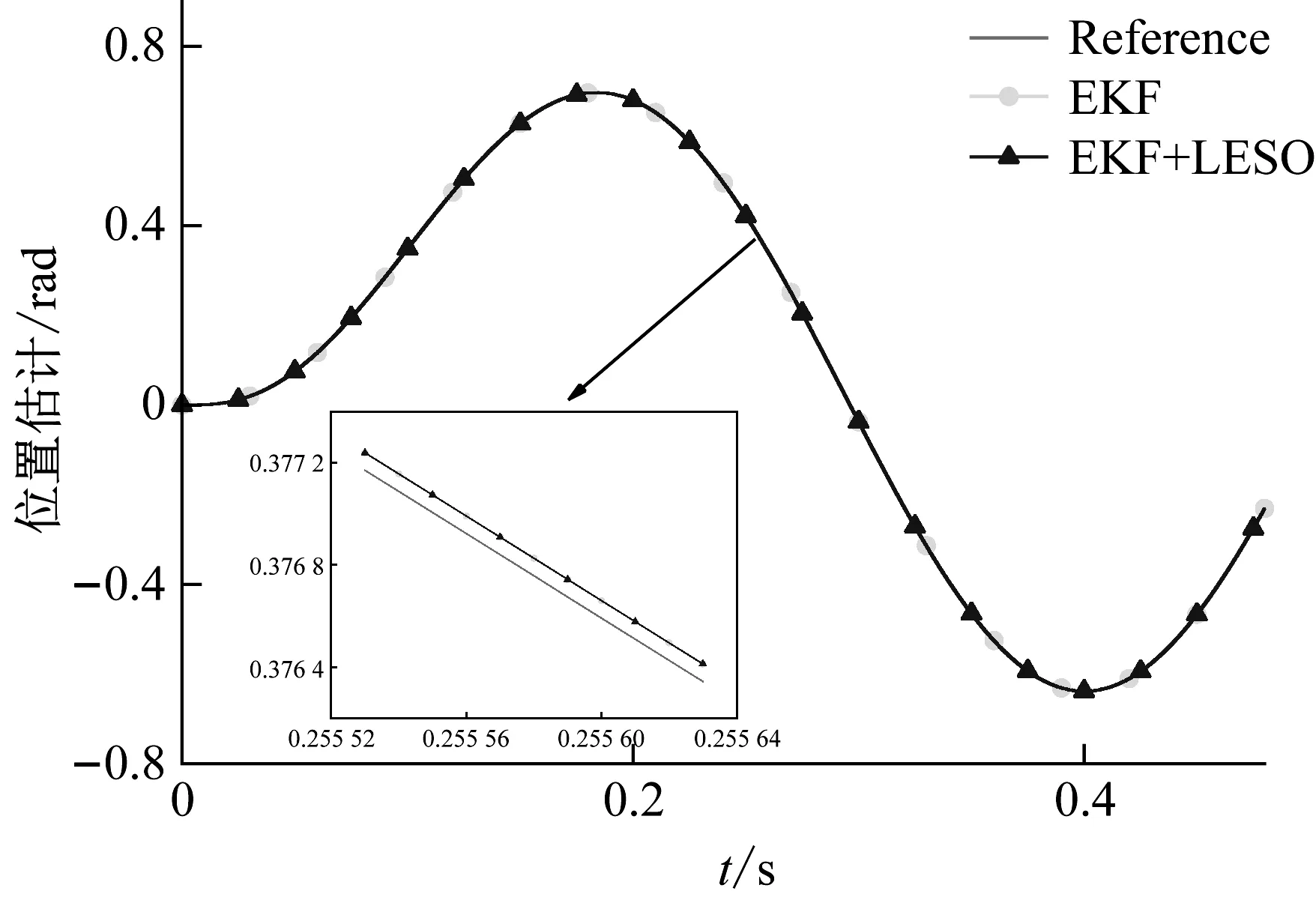
(a)

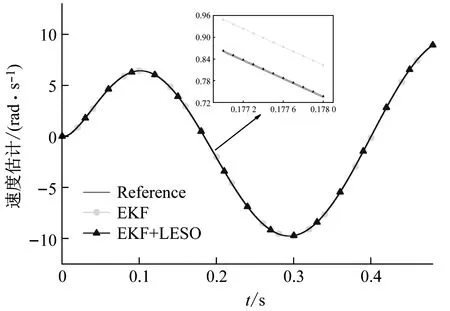
(B)图4 级联观测的状态估计曲线Fig.4 State estimation curve of cascading observation

图5进一步给出了在EKF提供的转角“粗估计值”存在直流偏差Δy=0.2时对转速的级联观测情况。EKF的粗估计最大误差为-0.102 6，远大于EKF+LESO (0.004 7)，可见级联观测的精度仍有较大提高。

4.1.2 系统跟随能力、抗扰能力验证

图6给出了设计系统对不同期望位置信号(单位常值信号，单位幅值、频率20 Hz的正弦信号)的跟随曲线，在一定程度上反映了整个系统的控制性能。对常值信号的跟随过程平稳无超调，跟踪精度较高(误差为5.34×10-4)。在对定频信号的跟随上则出现了明显的相位滞后，增大控制器带宽wc则能有效减轻滞后的影响，这是因为整个LADRC按照模型(11)等效，其跟随规律符合自动控制原理中二阶系统的频响关系。同时这种构建方式省去了速度环控制，更利于控制上滞后程度的减轻。

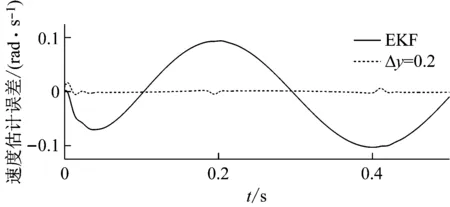
图5 转速级联观测的误差曲线Fig.5 Cascading observation error of speed

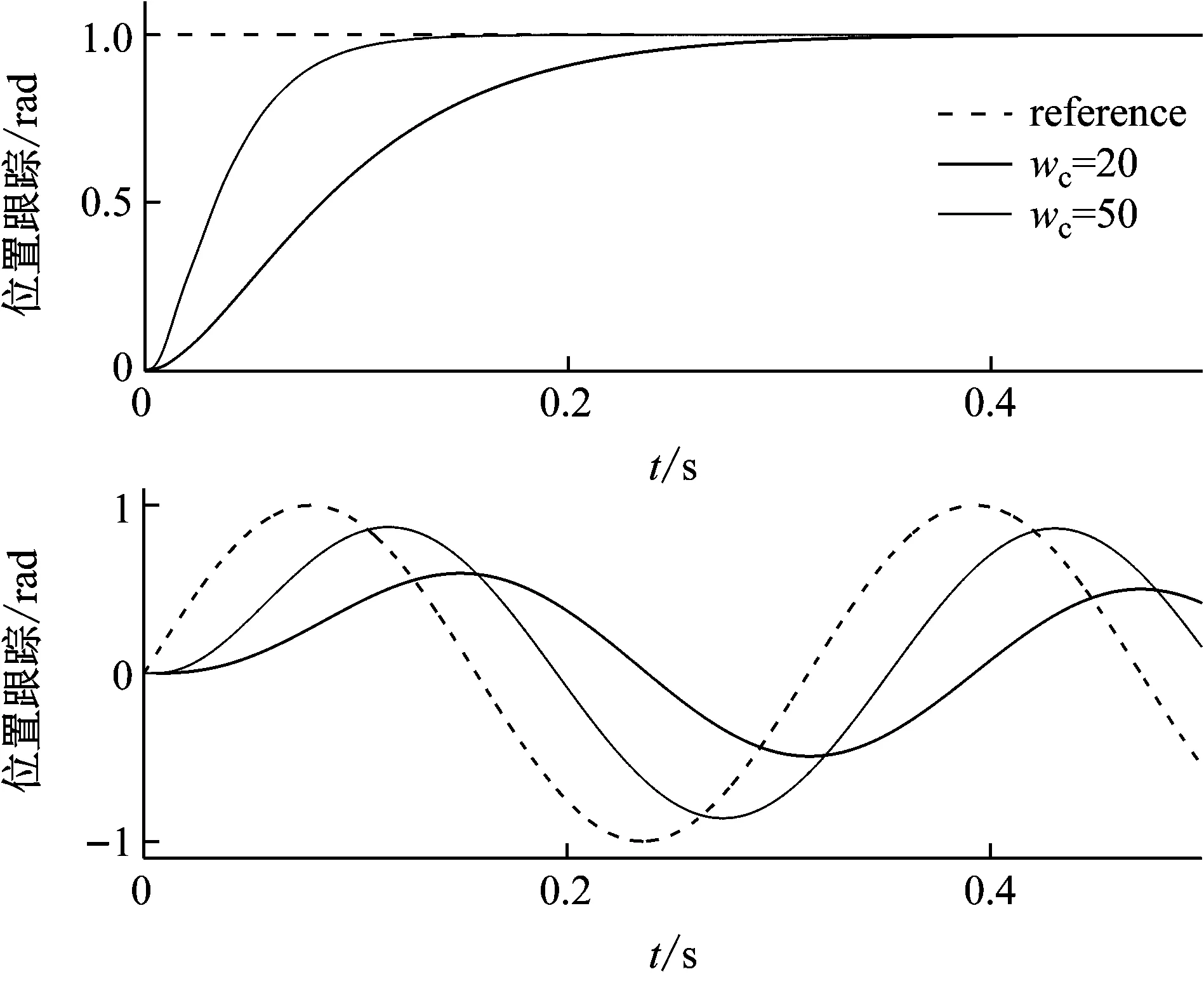
图6 位置跟随曲线Fig.6 Position tracking curve

针对PMLSM敏感扰动的特点，在常值期望输入下做了LADRC与三环PI的抗扰对比仿真，扰动为幅值1 N·m、在0.3 s阶跃的负载力矩。位置环与速度环的PI参数分别为[30,2]、[0.7,20]。图7给出了跟踪对比情况，在响应速度上PI控制占据优势，这是由于经典PI控制多串联了速度环的控制器，因此在动态控制上灵活性、可控性较强，但同时也存在参数整定繁琐的弊端。加载扰动后，显然LADRC的扰动抑制能力更出色，调节时间更快，这是由自抗扰控制的本质特征决定的——通过观测和实时反馈，将原来PI控制恒定速率的误差收敛变为直接从初始控制量中减去总扰项，从而大大加快了控制量的调整速度，使得系统应对突变扰动有着更快的响应表现，从而提高了整体的扰动抑制效果。

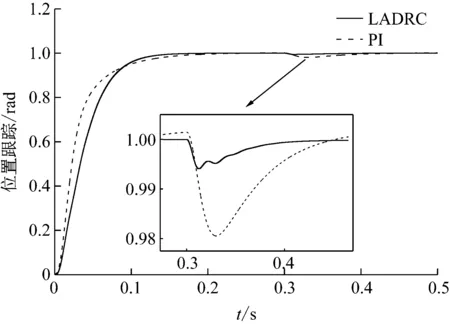
图7 位置跟随曲线(含扰动)Fig.7 Position tracking curve (with disturbance)

4.2 实 验

实验中使用了北京灵思创奇公司生产的仿真器及研发型交流伺服驱动器。仿真器中集成了Ti公司的DSP芯片TMS320F28335，在MATLAB/Simulink中使用DSP仿真包搭建控制模型，编译、下载至仿真器中。驱动器选择IGBT-PWM模式，支持DSP输出的PWM波直接控制逆变器，基于空间电压矢量调制技术为PMLSM提供驱动电压。逆变器死区设置2.3 μs，直流端电压使用稳压电源30 V。为保证足够的EKF运算时长，相电流与位置采样频率分别设置5 kHz、1 kHz。系统中安装了精度为±2((m的光栅尺为速度估计提供参考。实验系统搭建如图8所示。

PMLSM为U型槽直线电机，具体系统参数：R=5.84 Ω，L=3.65 mH，Ψf=0.118 2 Wb，np=4，B=1.2 N·m/s，τ=16 mm，m=3.8 kg。受环境噪声影响，wo取150，wc设为30，不使用滤波器。电流环PI控制器取为[0.02,32]。

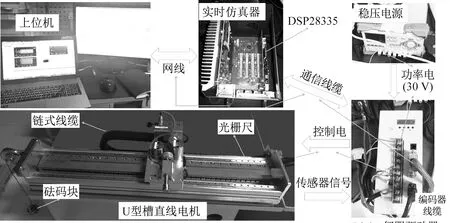
图8 PMLSM实验系统Fig.8 Laboratory test system of PMLSM

为针对性验证LESO的容错能力，EKF算法取为如下噪声矩阵：Q=diag[20,20,200,0.1]，R=diag[0.2,0.2]，比较速度估计效果及控制精度。

设计期望位置信号，使得速度在0～2.5 s、2.5～5 s分别以8、-8 mm/s3的加加速度运行，最终稳定在50 mm/s。图9给出了动子运行速度曲线，在加速过程中，EKF的估计值始终与真值偏差较大，且相位严重超前，LESO的估计值则能始终以较高的精度逼近真值。图10显示的估计误差更能直观表明这一点。10 s时刻电机开始拖动砝码块(0.25 kg)，动子速度出现了约0.5 mm/s的降幅，随后产生了震荡，这一过程中EKF对速度的估计出现了静差，震荡的均值速度约为53.7 mm/s，而LESO始终围绕真实速度，在50 mm/s处震荡，但振幅较EKF(0.282)大很多(1.193)。可见，EKF具有出色的滤波能力，虽然由于噪声矩阵的设置使其估计精度并不高，但经过LESO后速度的观测得到了校正，这也验证了LESO从含较大偏差的信号中提取中阶状态信息的“容错能力”。

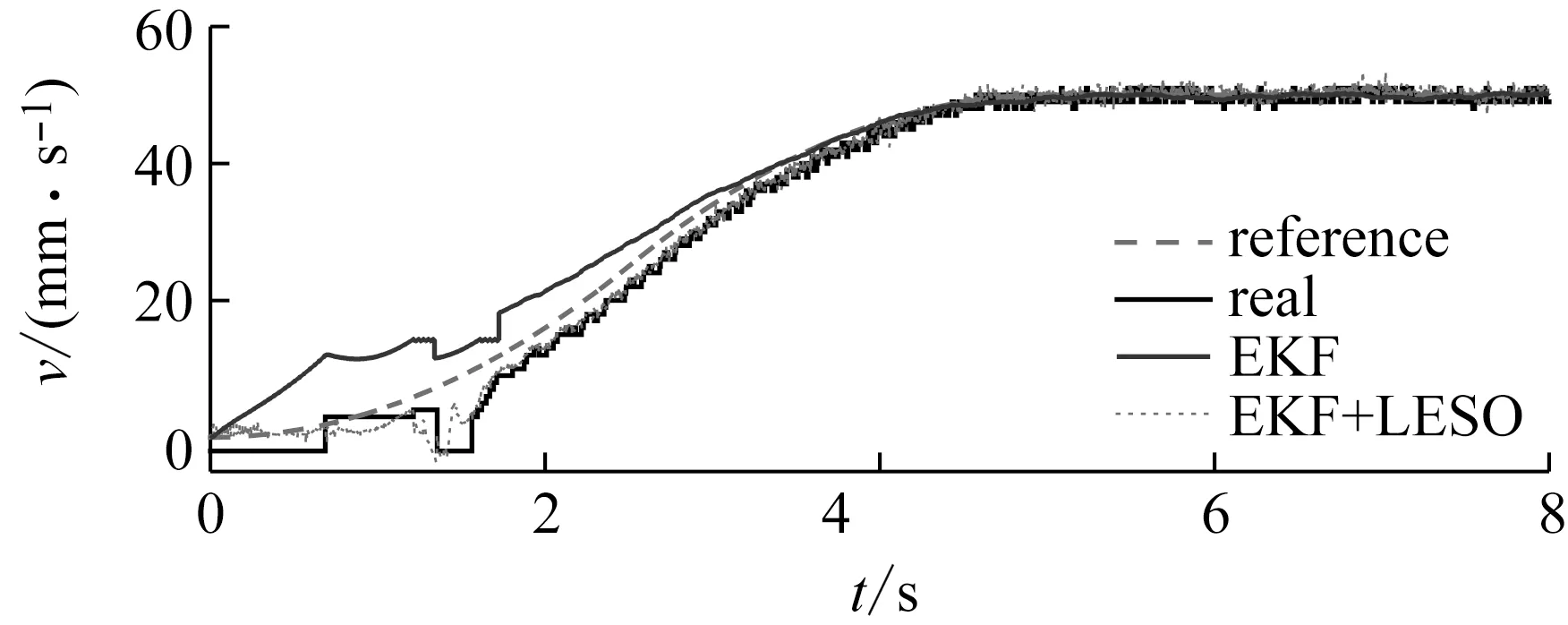
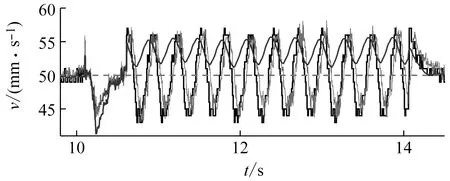
图9 动子速度曲线Fig.9 Speed curve of motor driver

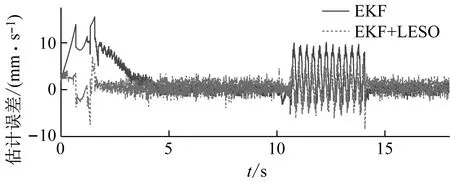
图10 速度跟踪误差、估计误差曲线Fig.10 Speed tracking and estimating error

对比电机真实运行速度与规划速度，在起步阶段，由于静摩擦的存在，实际速度与期望速度之间存在较大误差，前1.8 s追踪明显滞后，随后系统能够按照规划轨迹稳定运行，速度跟踪误差不超过±1.5 mm/s(图9)。带载运行时，系统出现了一定幅度的震荡(5.6 mm/s)，一部分原因在于未使用滤波器的缘故使得wo取值较小，观测精度受限，同时wc整定值较小，系统抵抗负载等扰动的刚度不够；另外为验证级联观测的有效性，EKF的估计精度也调得较低。但系统始终能够围绕期望速度稳定运行。

图11、12给出了在规划速度信号为幅值80，频率0.5的正弦信号输入下，级联观测系统的速度估计对比及整个PMLSM伺服系统的运行曲线。LESO对速度的观测引入了较多的噪声，但其均值始终跟随真值，这与图9、10的分析结论是一致的。注意到在6.4 s左右速度趋近0，此时LESO的观测出现了明显的“峰化现象”，这是扩张状态观测器的固有弊端。这种误差经反馈传递至控制率中，最终引起系统控制精度的突降(图12中控制误差由8 mm/s增至约20 mm/s)，对伺服系统的控制效果存在不利影响。但总体而言，在EKF取较差精度、不使用滤波器的前提下，整个无传感器控制系统依然能够平稳运行，体现出级联观测的有效性以及伺服系统较强的抗扰能力。

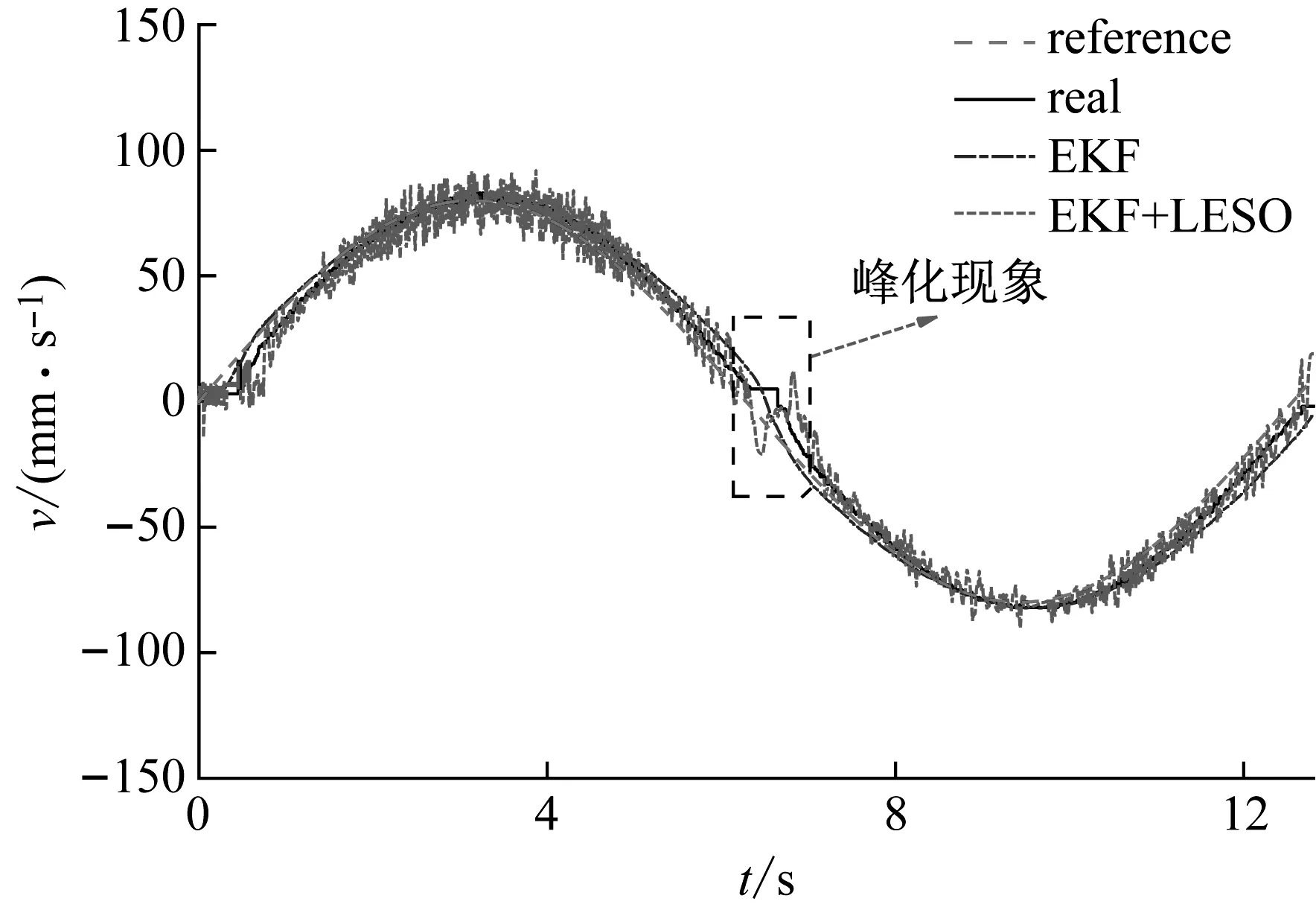
图11 速度曲线(幅度80，频率0.5 Hz)Fig.11 Speed curve of sin signal (80,0.5 Hz)

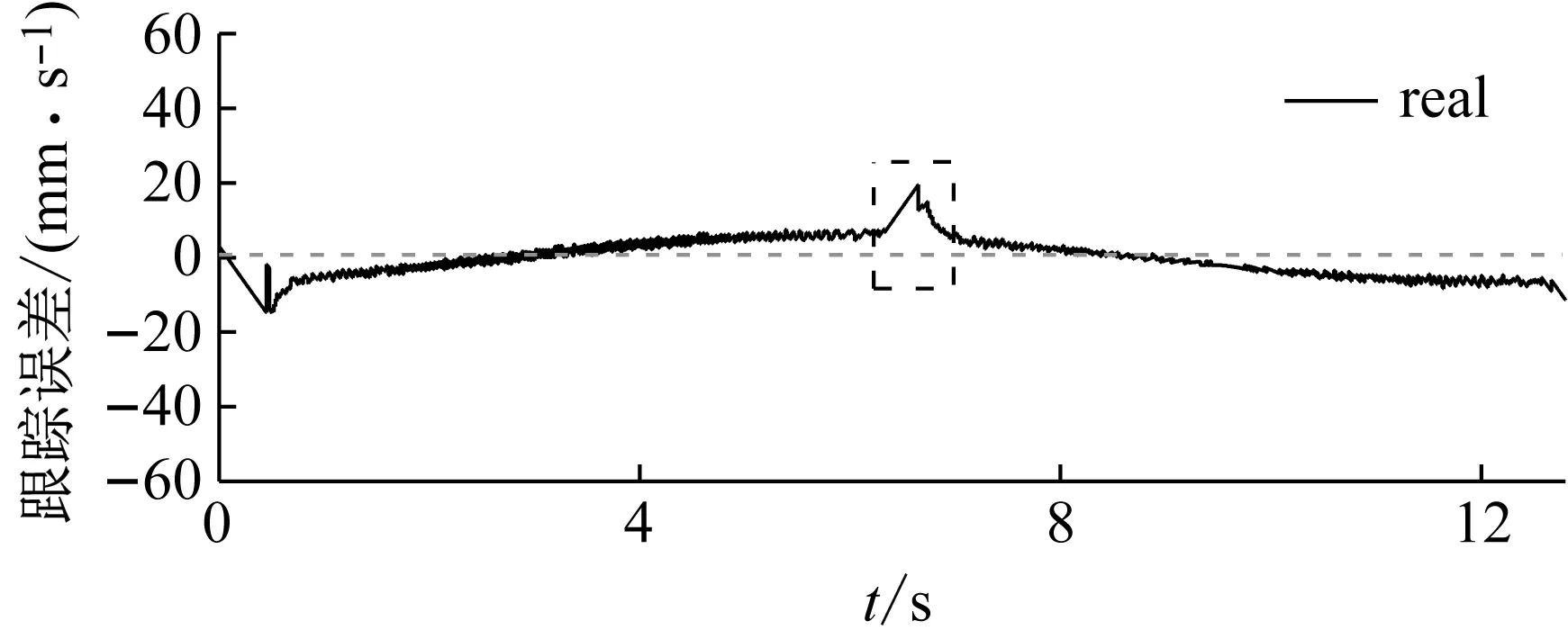
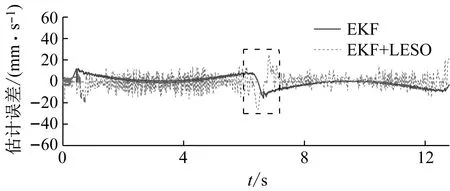
图12 速度跟踪误差、估计误差曲线Fig.12 Speed tracking and estimating error

5 结 论

为提高直线电机伺服系统的抗扰能力，抑制电机抖振的产生，设计了PMLSM的位置环线性自抗扰控制系统。为进一步摆脱速度传感器的束缚，在分析LESO观测精度的基础上，通过理论推导，得出在输入量测信号存在慢时变偏差的情况下LESO对中阶(2～n)状态的观测不受影响、具有一定容错能力的结论，进而提出了一种EKF+LESO的无传感器速度级联观测方式。仿真验证了LESO的容错性、级联观测系统对速度估计的准确性以及新系统的抗扰能力；实验结果则进一步表明，在建模不确定度、环境噪声客观存在的条件下，新系统能够对速度实现较高精度的观测，系统抗扰能力较强，具有良好的运行平稳性。针对LESO观测过程中出现的峰化现象，设计有效的抑制策略是下一阶段研究的重点。