隧道纵向地震反应分析的反应位移法对比

刘晶波，王东洋，谭 辉，宝 鑫

(清华大学 土木工程系，北京 100084)

反应位移法是研究地下结构横向抗震反应分析的一种拟静力方法，具有计算模型简单、精度较高、实施步骤明确等优点，已被编入我国多部规范中[1-3]，是我国地下结构抗震领域广泛采用的设计方法。近年来，实用性较高的反应位移法在地下隧道结构纵向地震反应分析中也有应用[4-6]，并被《城市轨道交通结构抗震设计规范》(GB 50909—2014)所采用(以下简称“规范”)。规范纵向反应位移法沿用了经典反应位移法的基本思想，认为地下结构在地震作用下的反应主要取决于周围土体的运动[7]，通过建立地基弹簧来模拟周围土体对结构的约束作用：将隧道结构简化为梁单元、周围地基土简化为支撑结构的地基弹簧，把沿隧道纵向轴线分布的土层位移作为等效地震作用施加于地基弹簧的非结构连接端，完成静力计算以获得隧道结构的地震反应。

尽管经典反应位移法具有较为严谨的理论基础，但已有研究表明该方法在计算地下结构横向地震反应时有时存在较大误差[8-10]，主要原因是经典反应位移法计算模型中地基弹簧刚度系数不易确定，离散的地基弹簧无法反映地基土层自身相互作用。因此，同样采用地下结构-地基弹簧计算模型的纵向反应位移法也可能存在相同的问题。

针对非一致地震动输入下隧道等长线型地下结构的抗震问题，文献[11]提出了适用于隧道结构纵向地震反应分析的整体式反应位移法，结合动力时程法验证了纵向整体式反应位移法具有良好的计算精度，并且可以简便的判读隧道结构纵向地震反应的最不利时刻。

本文以北京某地铁区间盾构隧道结构为对象，采用规范纵向反应位移法和文献[11]提出的纵向整体式反应位移法进行SH地震波斜入射时隧道结构的地震反应分析，并与动力时程法计算结果进行对比，以比较两种拟静力方法的计算精度和适用性。

1 规范纵向反应位移法

规范采用的适用于隧道纵向地震反应计算的反应位移法，将结构简化为梁单元，将周围地基土体简化为支撑结构的地基弹簧，把沿隧道纵向轴线分布的土层位移作为等效地震作用施加于地基弹簧的非结构连接端。

地基弹簧刚度可按土层的基床系数简单确定，或按静力有限元法计算。由于按基床系数的方法确定地基弹簧刚度时可能存在较大误差，本文采用静力有限元法计算了地基弹簧的刚度。

规范建议了两种等效地震作用计算方法——假定为正弦波型或采用自由场位移时程。为论述方便，本文将正弦波型等效地震作用称为规范方法一、将采用自由场位移时程的方法称为规范方法二，分别讨论二者的计算过程和计算结果。

1.1 规范方法一

如图1所示，沿隧道纵向轴线为坐标x轴，垂直于隧道纵轴的水平方向为坐标y轴。入射波传播方向与隧道纵轴在同一水平面内，二者夹角为φ。采用简化方法确定沿隧道纵轴分布的土层位移。

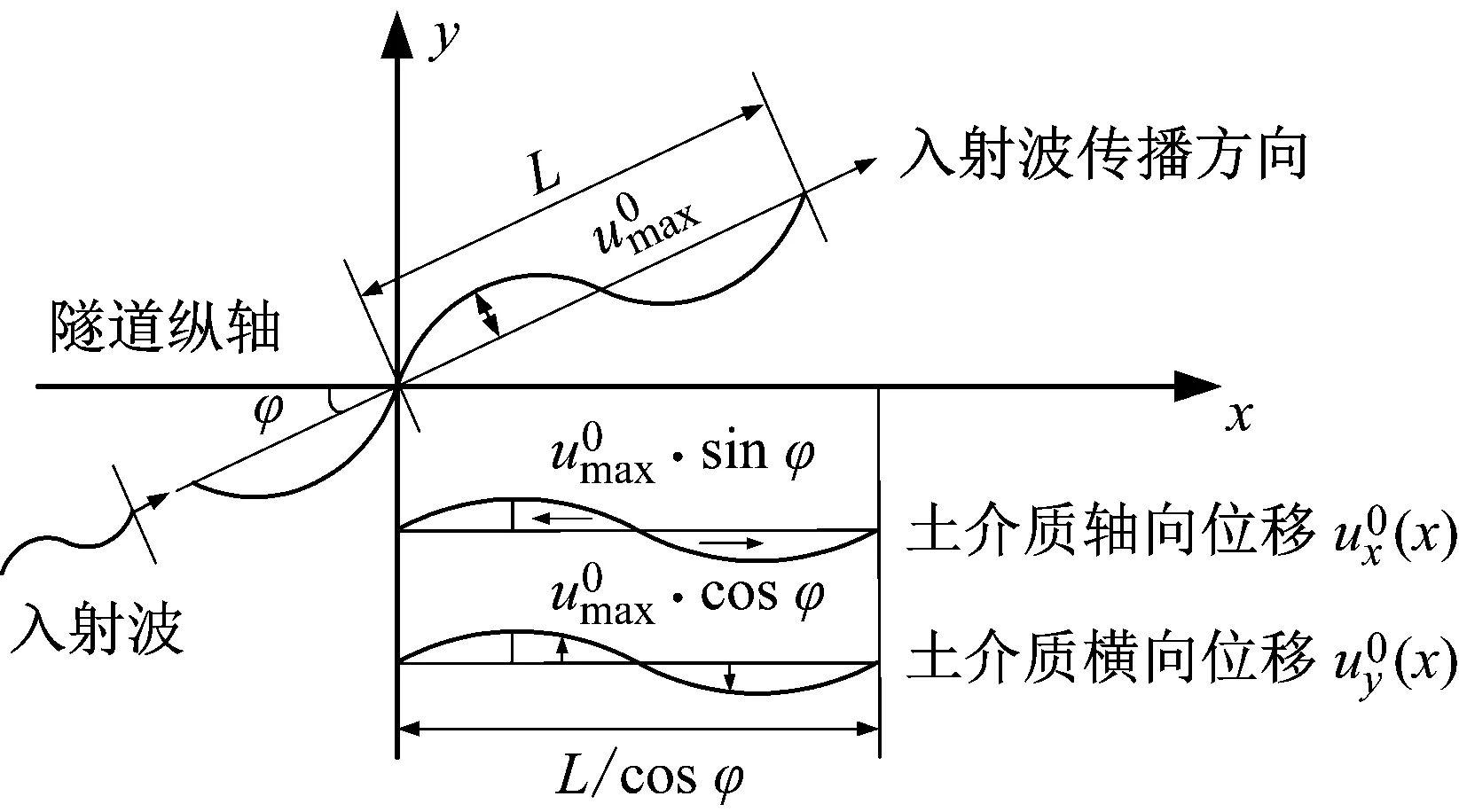
图1 规范方法一土层变形示意图Fig.1 Deformation of soil medium subjected to the seismic wave input with the incident angle φ

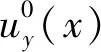
(1)

L=2L1L2/(L1+L2)

(2)

L1=Ts·VSD

(3)

L2=Ts·VSDB

(4)

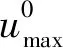
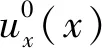
(5)

(6)

1.2 规范方法二

为了反映不同频谱成分地震波对隧道结构纵向地震反应的影响、解决纵向反应位移法在非均匀土层中的适用性，直接采用自由场位移时程作为等效地震作用[12]。该方法首先需要计算土层模型在地震作用下的真实位移响应，然后将隧道轴线所在位置处的各点自由场位移时程作为强制位移荷载施加在梁-弹簧模型中地基弹簧远离结构一端，据此求解各时刻结构纵向地震响应。

2 纵向整体式反应位移法

隧道结构作为一种长线型结构，它在地震作用下的纵向变形和内力受到地面运动空间变化的影响较大[13-14]。针对非一致地震动作用下隧道结构纵向地震反应问题，采用地下结构横断面地震反应整体式反应位移法的基本原理[15-16]，将横截面尺寸较小的隧道结构简化为埋置于土层中的弯曲梁，提出了适用于地下隧道纵向地震反应分析的整体式反应位移法。

该方法的关键环节在于确定隧道结构地震反应最不利时刻，将结构动力时程分析转换为等效静力问题求解。如图2所示隧道结构埋置于弹性半空间模型中，笛卡尔坐标系中x轴和y轴分别为两水平方向，z轴为竖直方向，地震SH波由远场斜入射至计算区域，入射方向与竖直方向夹角为θ、在水平面内投影与纵向x轴夹角为φ，隧道结构中心线的竖向坐标为zh。

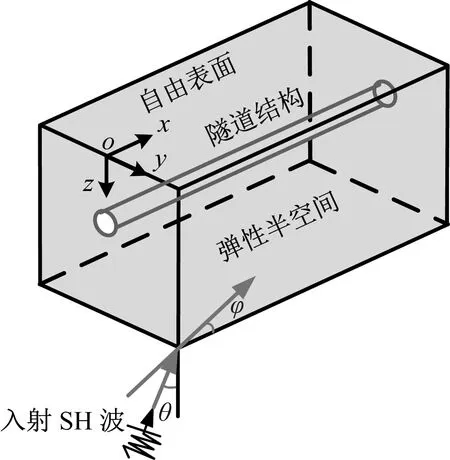
图2 埋置于弹性半空间中的隧道结构Fig.2 Tunnel structure embedded in elastic half-space

根据弹性半空间波动传播特点，结合自由场位移解和梁的弯曲理论，得到关系式(7)～(11)

(7)

(8)

(9)

(10)

(11)

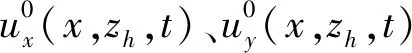
根据式(7)～(11)可以确定结构地震反应最不利时刻：对于隧道中任一点横向或轴向位移，最不利时刻为该点自由场横向或轴向位移的峰值时刻；相应于轴力的最不利时刻为该点自由场轴向速度达到峰值时刻；相应于弯矩的最不利时刻为该点自由场横向加速度达到峰值时刻；相应于剪力的最不利时刻为该点自由场横向位移对时间的三阶导数达到峰值的时刻。

确定了最不利时刻后，建立自由场有限元模型，将相应于隧道结构不同地震反应最不利时刻的自由场位移施加于自由场有限元模型中的对应隧道-地基交界面S位置处，静力计算获得界面S上的有限元节点反力，即为相应于不同物理量的等效输入地震动荷载。

将等效输入地震动荷载施加于隧道-地基整体有限元模型中的结构-地基交界面S有限元节点上，完成静力分析计算获得隧道结构的最不利地震反应。

3 计算模型和参数

文献[8]的研究结果表明，当入射SH波传播方向与隧道纵轴在同一水平面内(即θ=90°)时，隧道纵向地震反应达到最大值：随着入射角φ增大，隧道横向位移、弯矩和剪力均逐渐减小，隧道轴向位移逐渐增大，而隧道轴力先增大后减小。若结合规范中“地基土层位移沿隧道纵向呈正弦波形式分布”的假定，则当φ=0°时，隧道横向变形及所受弯矩、剪力最大；当φ=45°时，隧道拉压变形及所受轴力最大。因此，为了研究SH波斜入射至弹性半空间时隧道结构的纵向地震反应，本文分别采用作者提出的纵向整体式反应位移法、规范方法一和规范方法二，计算θ=90°时SH波以φ=0°、φ=45°两种角度入射时隧道结构的纵向地震反应，并结合动力时程法对比两种拟静力方法的计算结果。需要说明的是，下文所有计算结果中隧道结构横向位移值、弯矩值和剪力值是在地震波入射角φ=0°时计算得到；隧道结构轴向位移值和轴力值是在地震波入射角φ=45°时计算得到。

以北京某地铁区间隧道为研究对象，结构顶部埋深为12 m，纵向长度取为300 m。衬砌结构采用C50钢筋混凝土平板型管片，内直径为5.4 m，外直径为6.0 m。假设隧道所在土层是均匀的，其质量密度ρ为2 000 kg/m3，剪切波速cs为300 m/s，泊松比ν为0.3。

土体-隧道结构三维有限元分析模型如图3所示。隧道结构采用梁单元模拟，土体采用实体单元模拟。在纵向整体式反应位移法的静力计算和动力时程分析中，建立尺寸相同的有限元模型，纵向x方向为300 m、水平y向为40 m，竖直z向为50 m。沿坐标x、y方向的单元尺寸分别为3 m和5 m；沿坐标z方向的单元尺寸有两种，在0～24 m深度范围内单元尺寸为4 m，其余为5.2 m。应用纵向整体式反应位移法计算时，有限元模型的四个侧面和底面采用固定边界条件；应用动力时程法计算时，有限元模型中土体单元的四个侧面和底面采用粘弹性人工边界，隧道两端截断处为自由边界条件。应用规范方法计算时，图3所示有限元模型中的土体单元被简化为沿隧道结构纵向布置的拉压地基弹簧和剪切地基弹簧，地基梁纵向长度仍为300 m，单元尺寸为3 m。

为了反映不同频谱成分地震波对隧道结构纵向地震反应的影响，选用El Centro波、Kobe波、Loma Prieta波三种实际地震动记录进行计算，地面峰值加速度为0.1g，三种地震波的加速度时程曲线如图4所示。

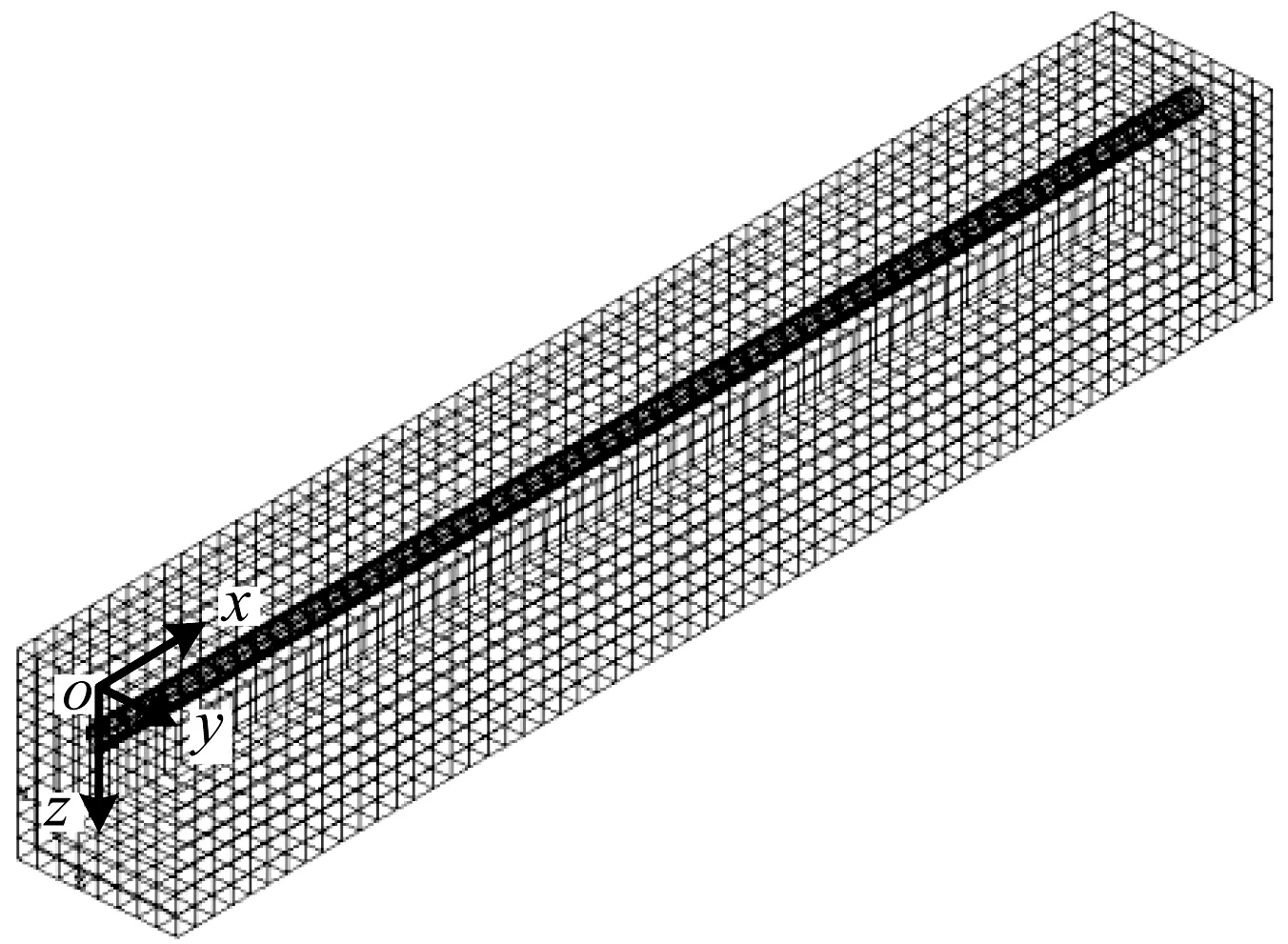
图3 土-隧道有限元计算模型Fig.3 Soil-tunnel finite element analysis model

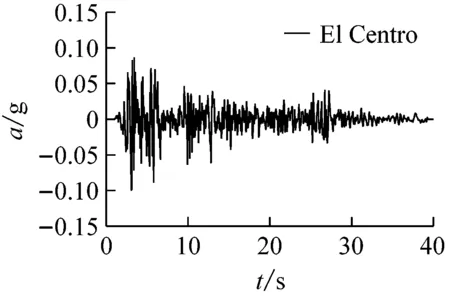
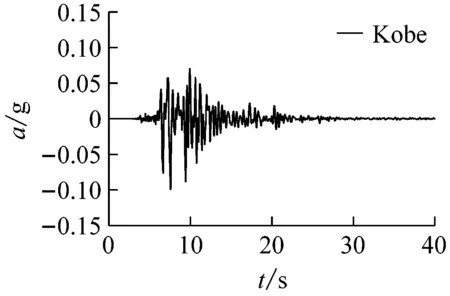
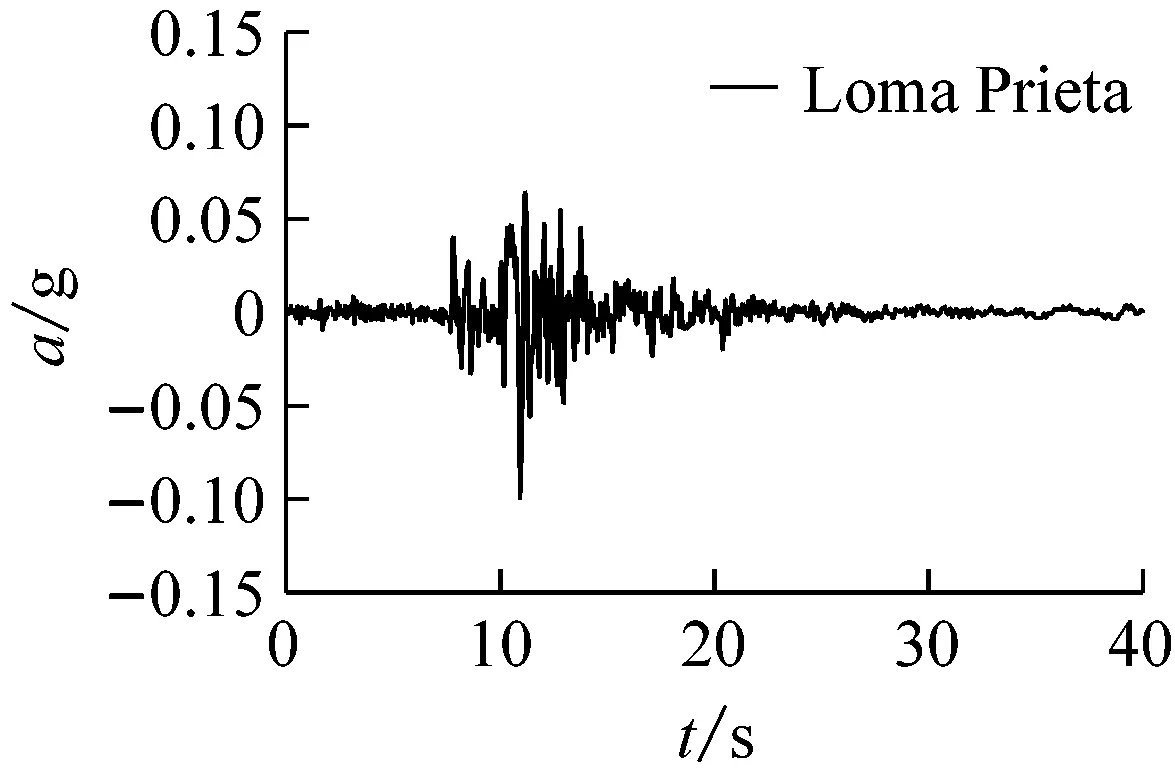
图4 地震波加速度时程曲线Fig.4 Acceleration time-history curve of ground motion

4 方法对比

4.1 规范纵向反应位移法计算结果

采用静力有限元方法计算地基弹簧刚度系数：建立挖去结构的土体有限元模型，图5为计算模型示意图，模型侧面和底面采用固定边界条件，在对应隧道结构位置处分别沿隧道横向和纵向施加单位强制位移δ进行静力计算，根据反力得到计算模型中拉压地基弹簧刚度系数kt=4.579×108N/m和剪切地基弹簧刚度系数kl=3.365×108N/m。

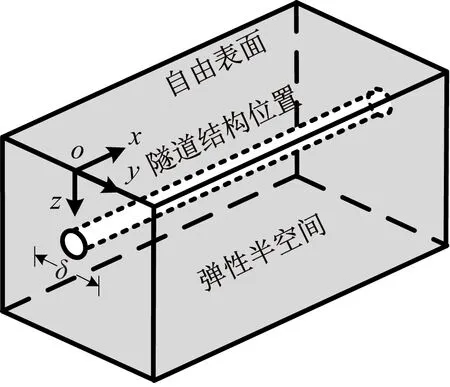
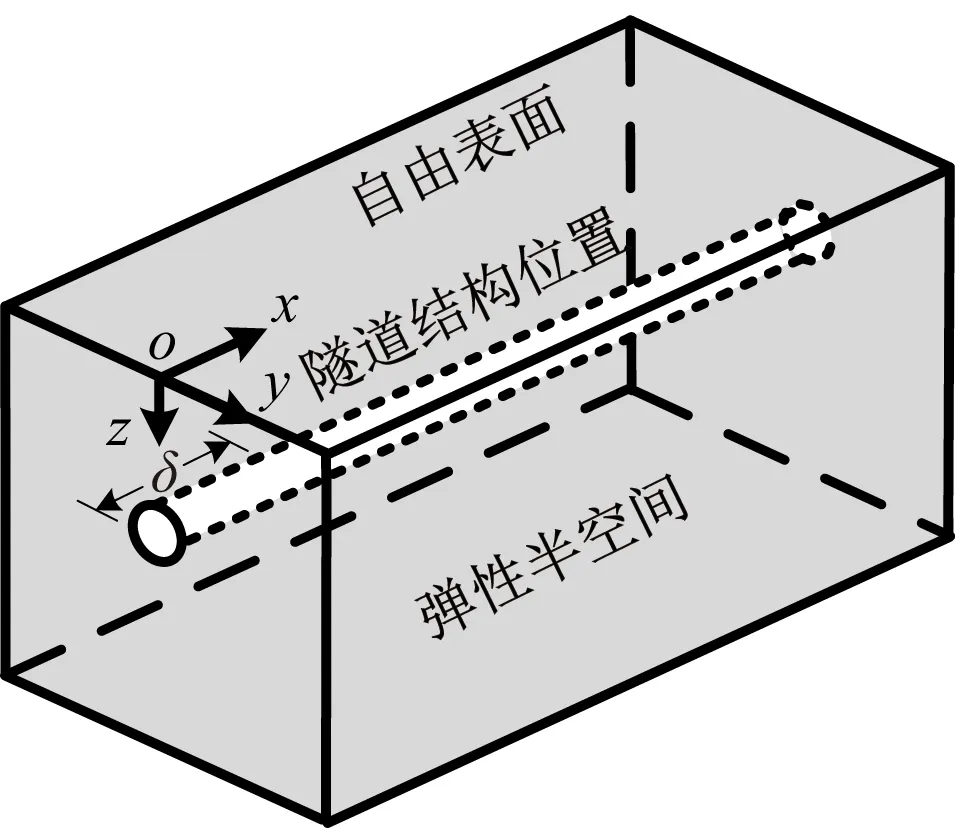
图5 静力有限元法计算地基弹簧刚度系数Fig.5 Stiffness coefficient calculation by the static finite element method

4.1.1 规范方法一

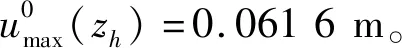
表1 规范方法一计算参数Tab.1 Calculation parameters of the specification method

由式(5)～式(6)得到入射角φ=0°、φ=45°时隧道埋深位置处沿纵轴的土层水平位移分布，如图6所示，将等效地震作用沿隧道纵轴布置于地基弹簧远离结构一端，完成静力计算，表2列出了隧道纵向地震反应规范方法一的计算结果。

由表2的计算结果可以看出，正弦波形式的土层位移分布无法反映不同频谱成分地震波对地基土层运动的影响，不能模拟隧道结构的真实反应。

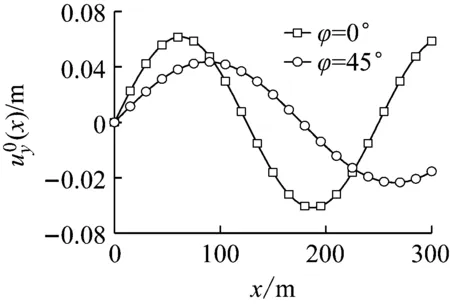
图6 隧道埋深处沿隧道纵轴的土层位移分布Fig.6 Displacement distribution of the soil layer

表2 规范方法一计算结果
Tab.2 Calculation results of the specification method

横向位移uy/m弯矩Mz/(kN·m)剪力Vy/kN轴向位移ux/m轴力Nx/kN0.061520162.2422.330.035459649.3

4.1.2 规范方法二

逐次提取每一时间步下对应隧道埋深位置处的自由场位移，沿纵向布置于隧道-地基弹簧模型上，依次完成各个时间步的静力计算，得到隧道结构一系列位移和内力反应。在本文算例中，对于每条地震波，采用规范方法二时共完成了8 000步静力计算，获得了结构纵向地震反应峰值。表3列出了隧道中点位移和内力反应峰值。

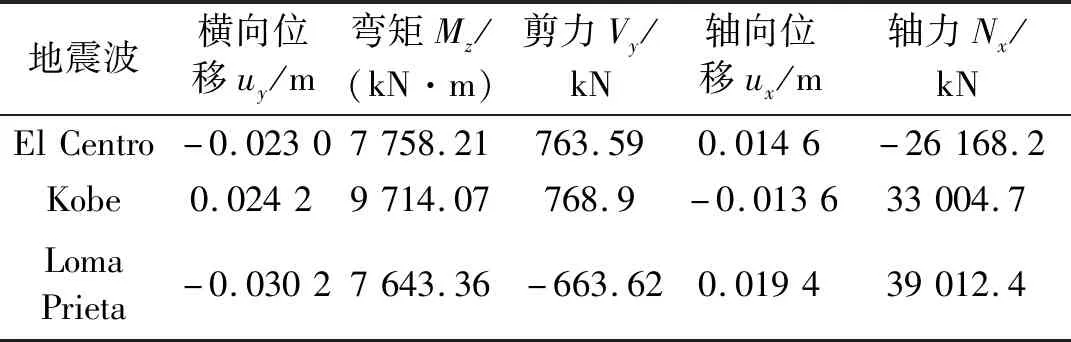
表3 不同地震波作用下规范方法二计算结果Tab.3 Calculation results of the specification method subjected to different seismic-wave recordings

4.2 纵向整体式反应位移法计算结果

图7(a)～图7(c)分别为El Centro波、Kobe波和Loma Prieta波以φ=0°入射时，对应于隧道中点(即x=150 m位置)横向位移、弯矩、剪力的自由场最不利变形。图8(a)～图8(c)分别为El Centro波、Kobe波和Loma Prieta波以φ=45°入射时，对应于隧道中点轴向位移和轴力的自由场最不利变形。

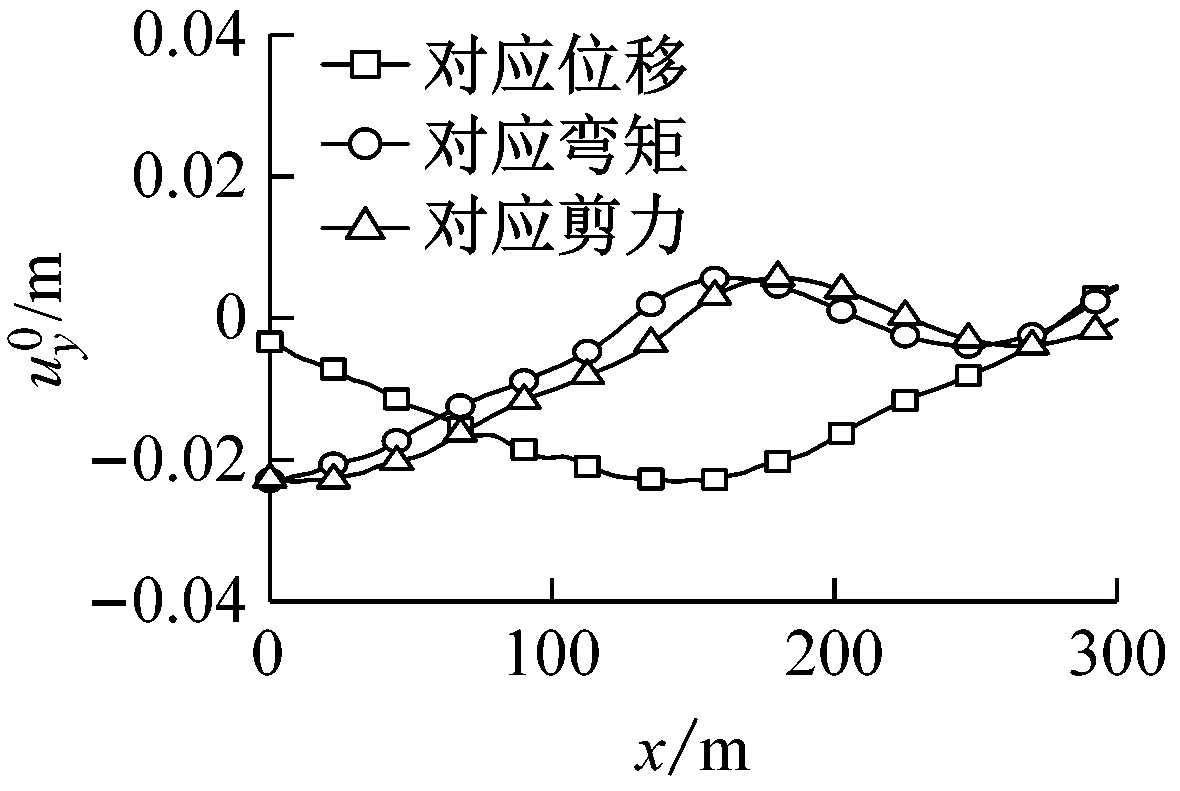
(a)El Centro波

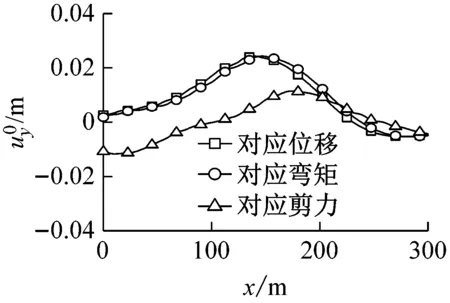
(b)Kobe波

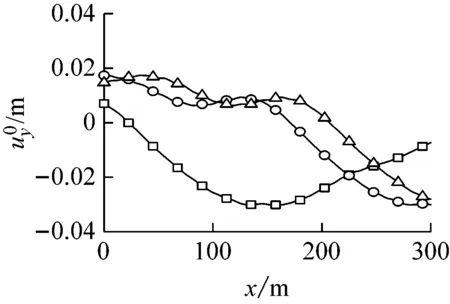
(c)Loma Prieta波图7 地震波入射角φ=0°时自由场最不利变形Fig.7 The least favorable free-field deformation(φ=0°)

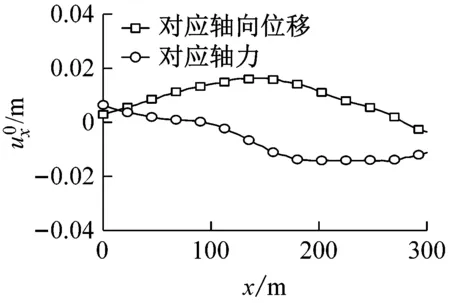
(a)El Centro波

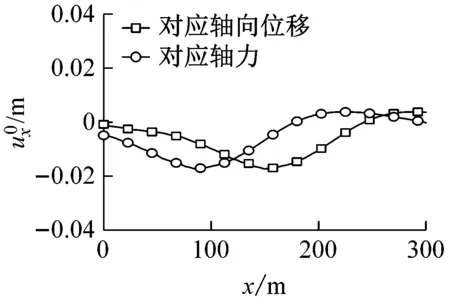
(b)Kobe波

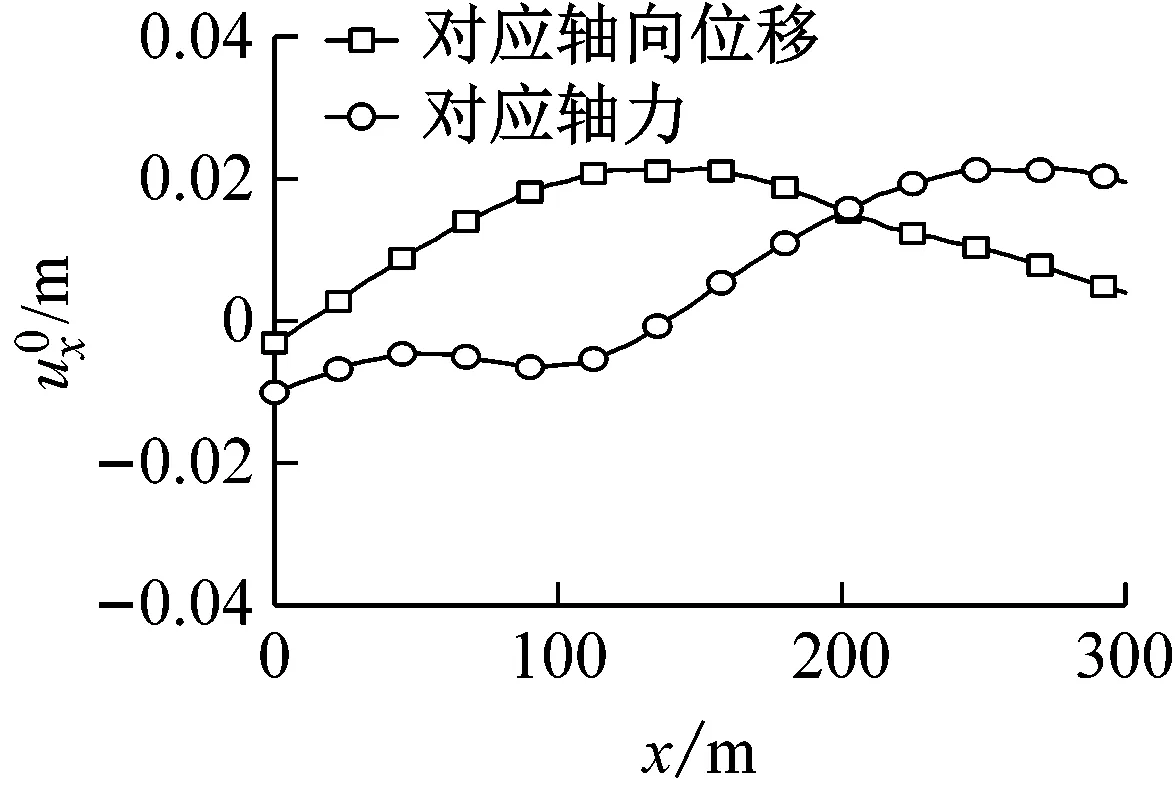
(c)Loma Prieta波图8 地震波入射角φ=45°时自由场最不利变形Fig.8 The least favorable free-field deformation(φ=45°)

表4给出了三种地震波以φ=0°、φ=45°入射时，隧道中点最不利地震反应及其相应的最不利时刻(表中圆括号内数值)。

4.3 动力时程法计算结果

通过波动方法实现地震波动的有效输入，采用时域逐步积分动力时程法完成隧道结构-地基动力相互作用系统的地震反应分析。计算得到的三种地震波输入条件下隧道结构中点位置处的位移、弯矩和剪力时程曲线分别如图9～图11所示。由图9～图11可以确定三种地震波入射时，隧道中点纵向地震反应峰值及其相应的峰值时刻，表5给出相应的计算结果(表中圆括号内数值为峰值时刻)。

4.4 三种方法计算结果对比

将三种地震波以两种角度入射时，纵向整体式反应位移法、规范方法一、规范方法二与动力时程法得到的结构地震反应对比汇总于表6～表8中，其中结构地震反应相对误差均为绝对值相对误差。

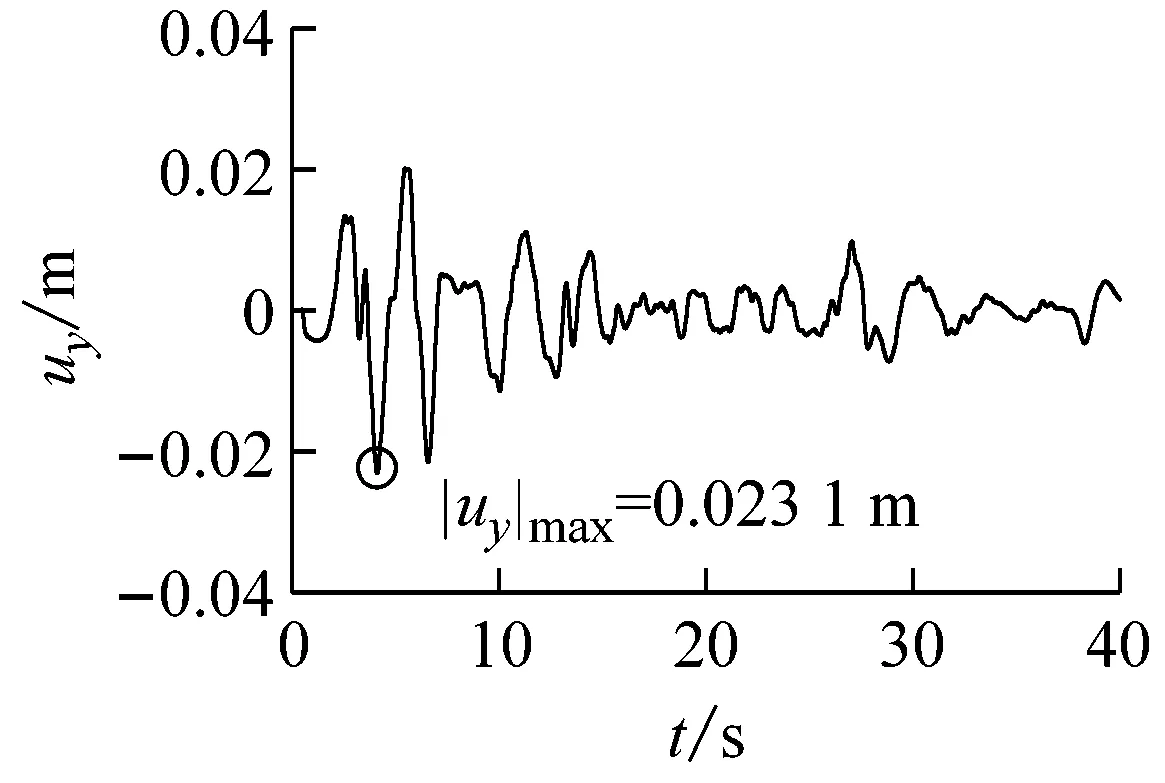
(a)隧道中点横向位移

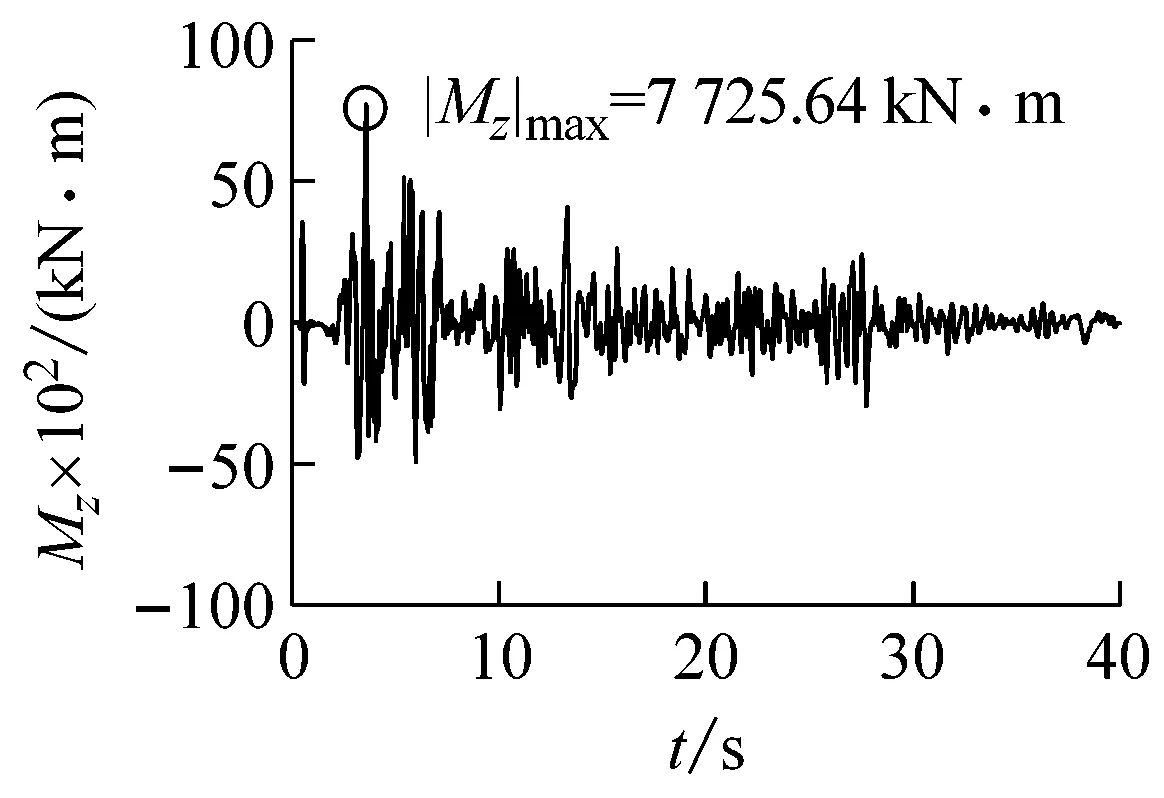
(b)隧道中点弯矩

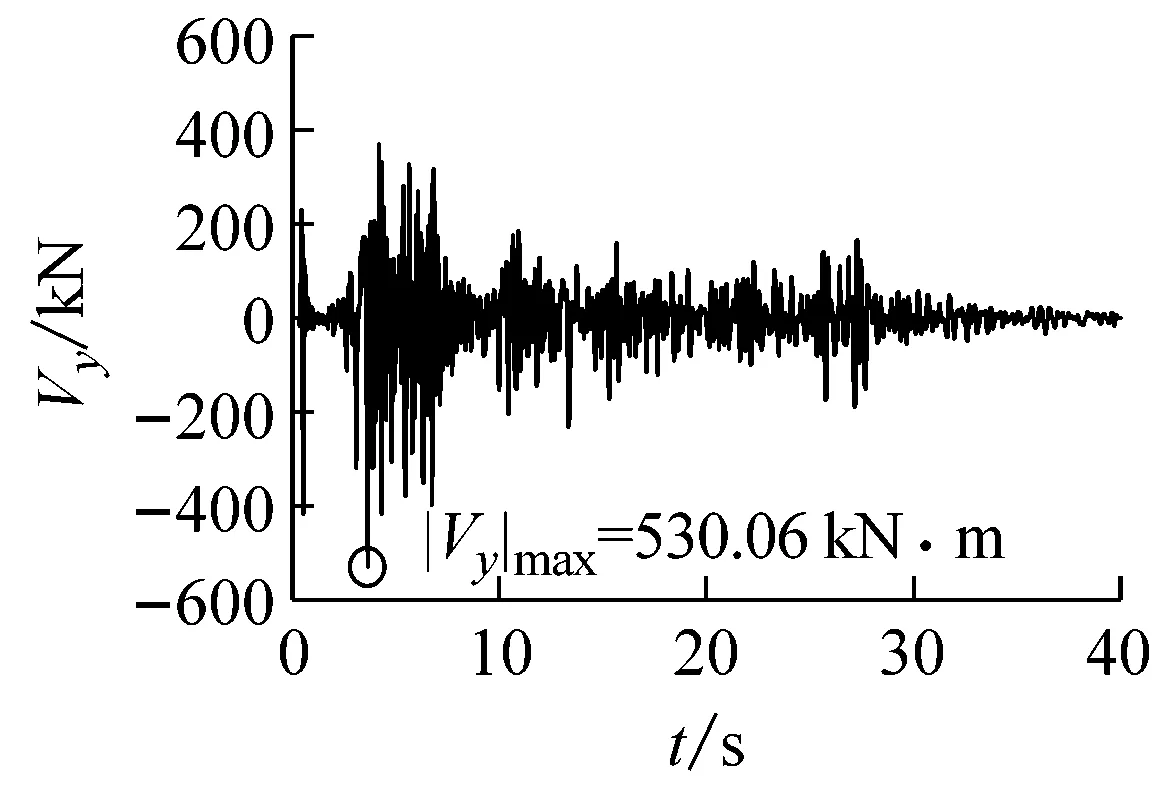
(c)隧道中点剪力

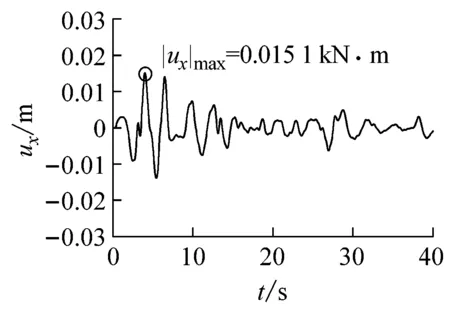
(d)隧道中点轴向位移

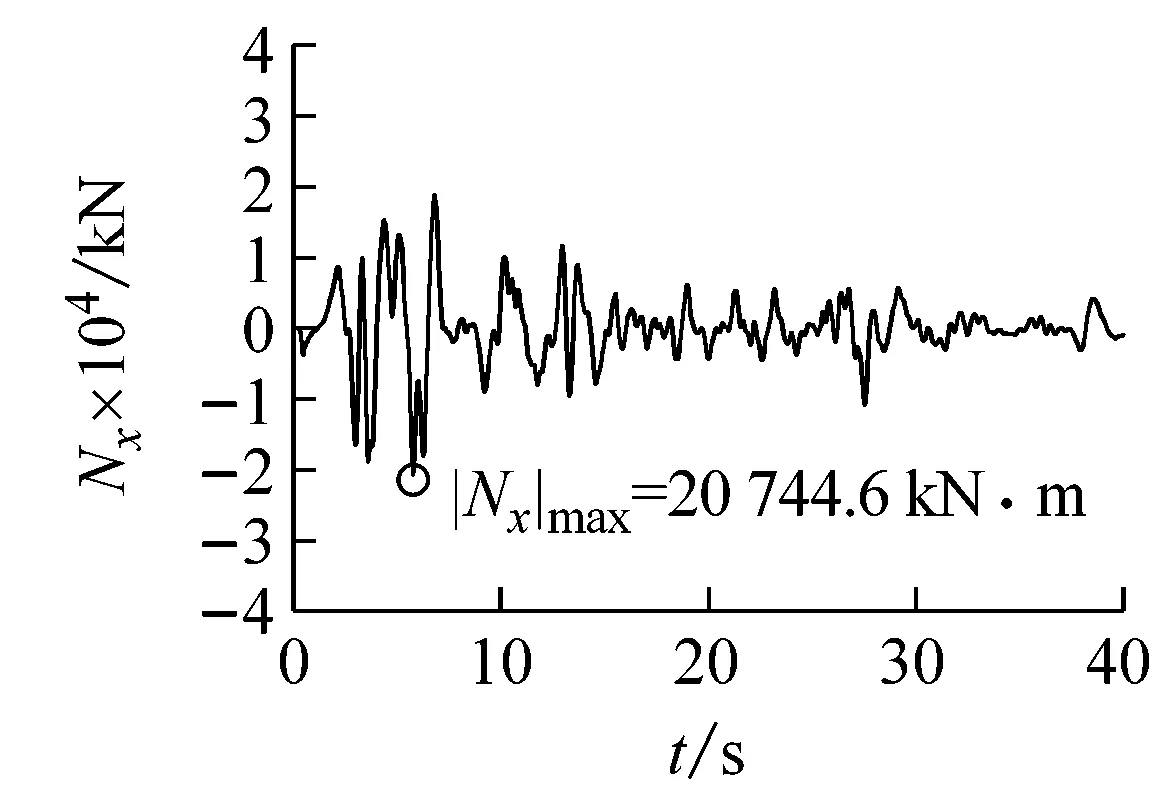
(e)隧道中点轴力图9 El Centro波输入时隧道中点地震反应时程曲线Fig.9 Seismic response time-history curve of the tunnel midpoint subjected to El Centro wave input

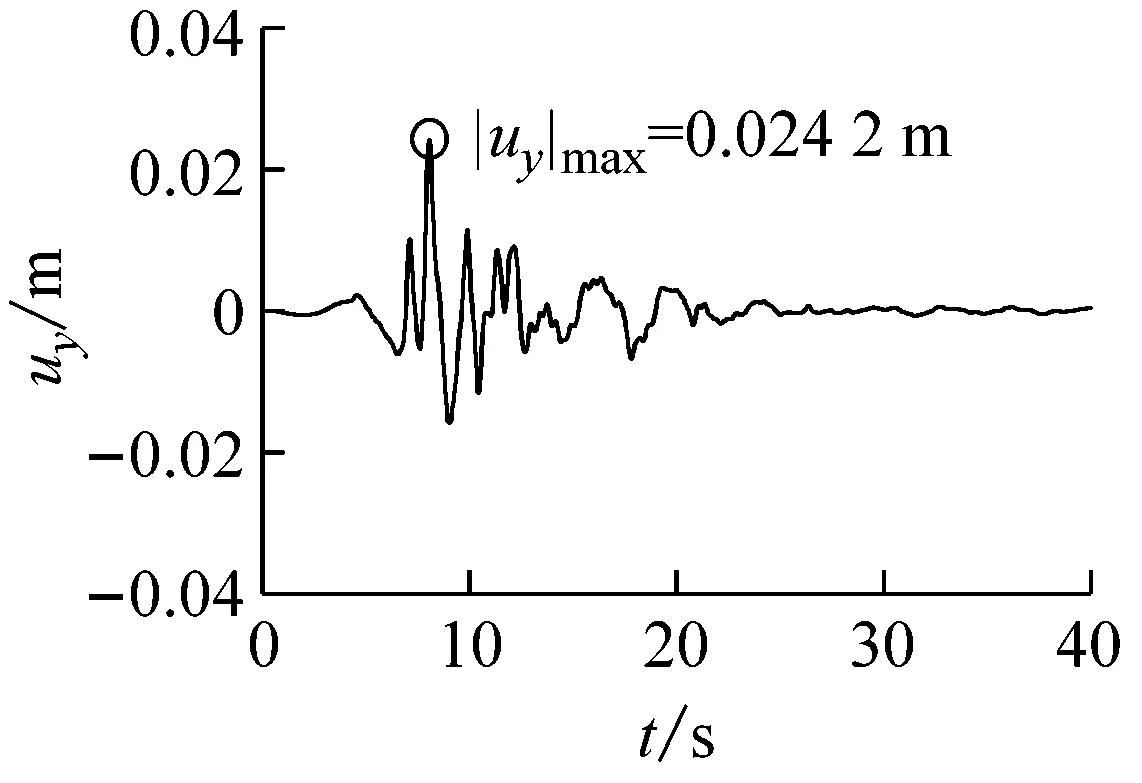
(a)隧道中点横向位移

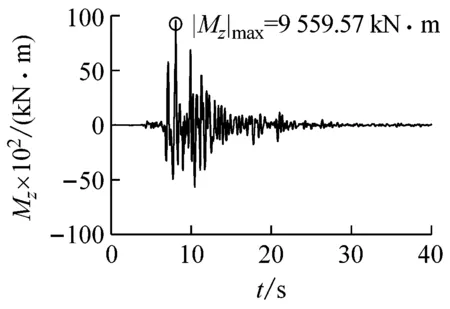
(b)隧道中点弯矩

(c)隧道中点剪力

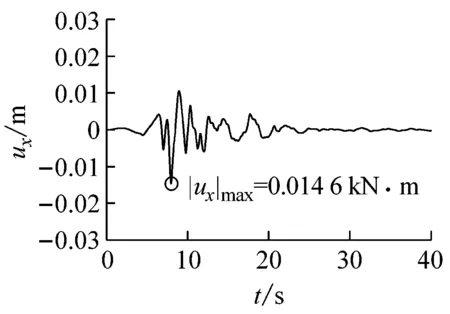
(d)隧道中点轴向位移

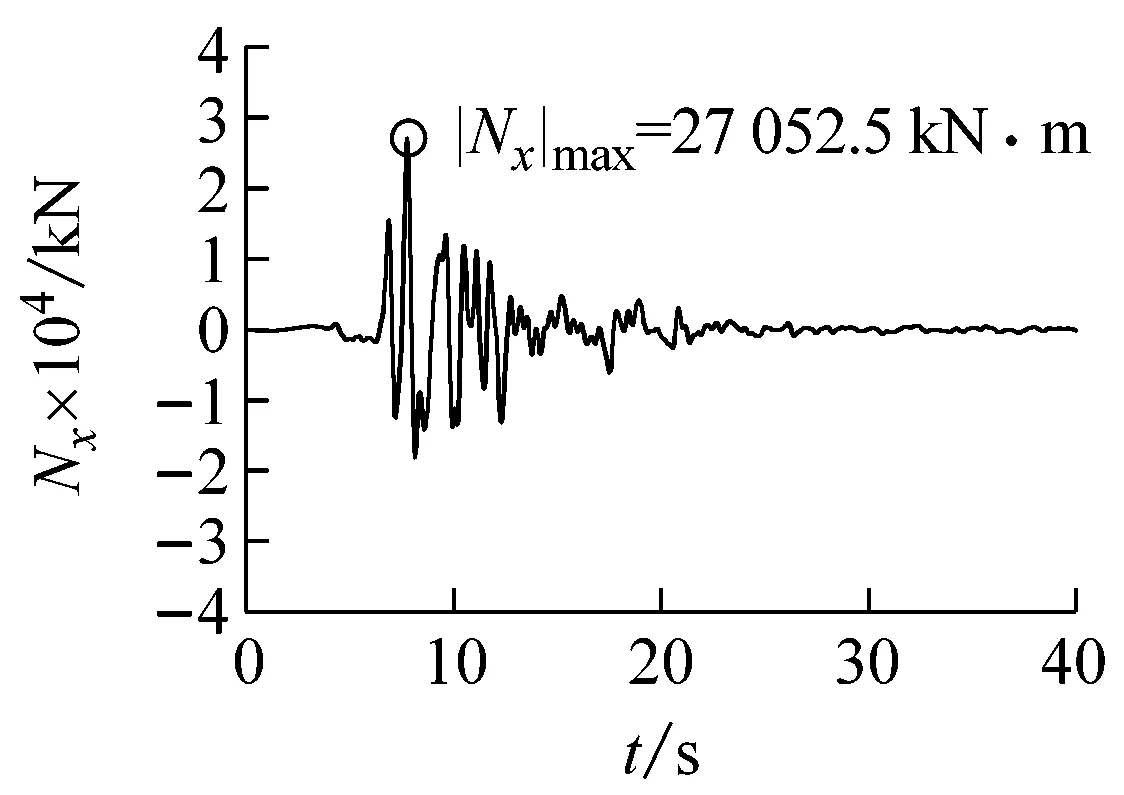
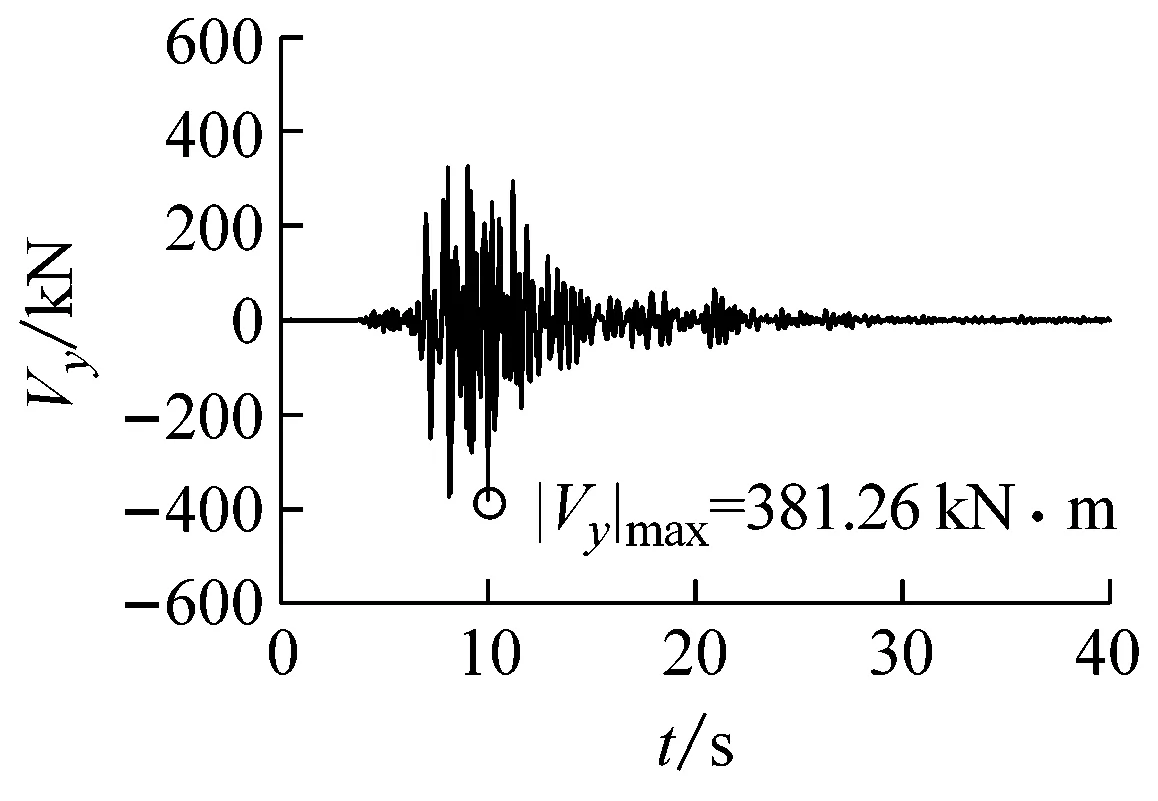
(e)隧道中点轴力图10 Kobe波输入时隧道中点地震反应时程曲线Fig.10 Seismic response time-history curve of the tunnel midpoint subjected to Kobe wave input

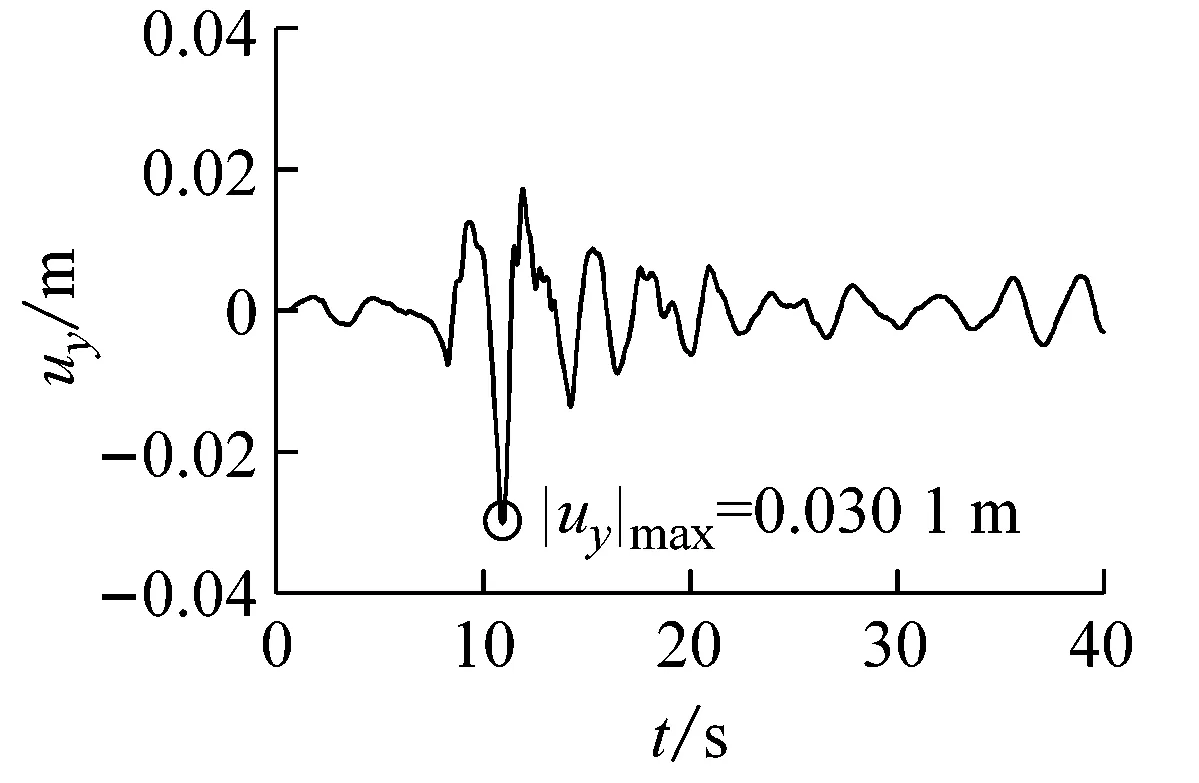
(a)隧道中点横向位移

(b)隧道中点弯矩

(c)隧道中点剪力

(d)隧道中点轴向位移

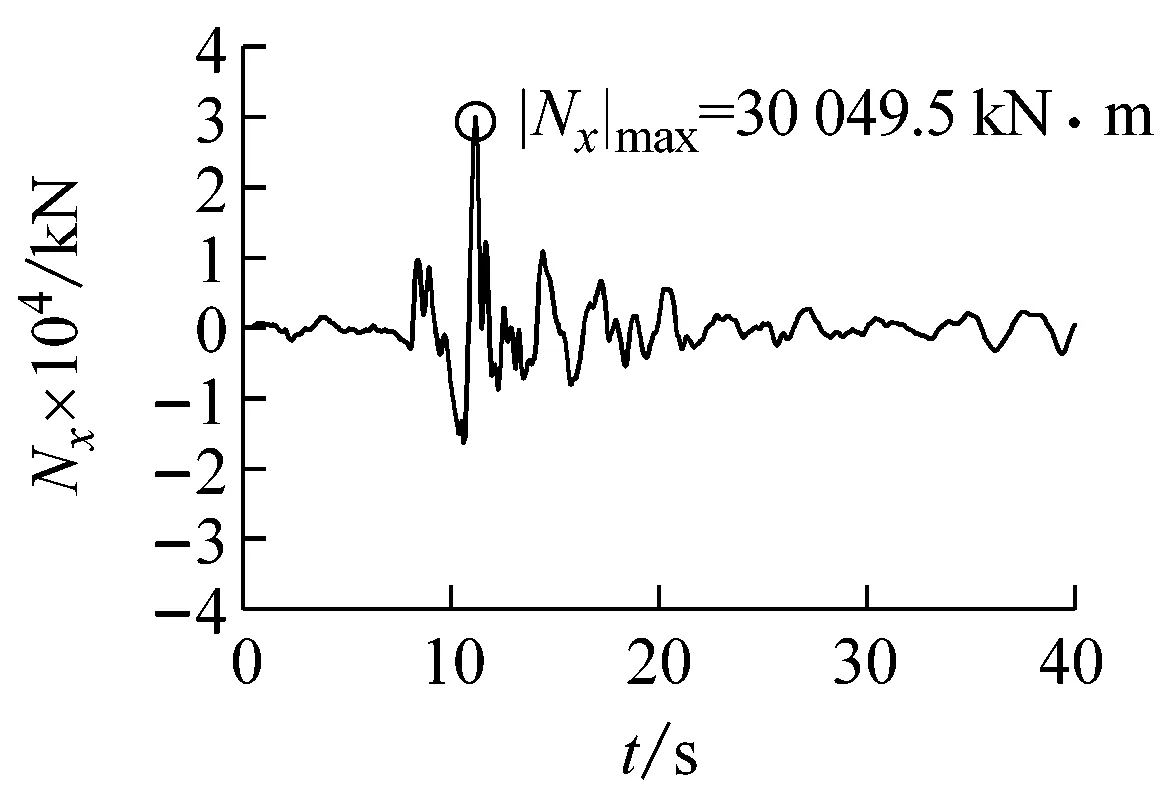
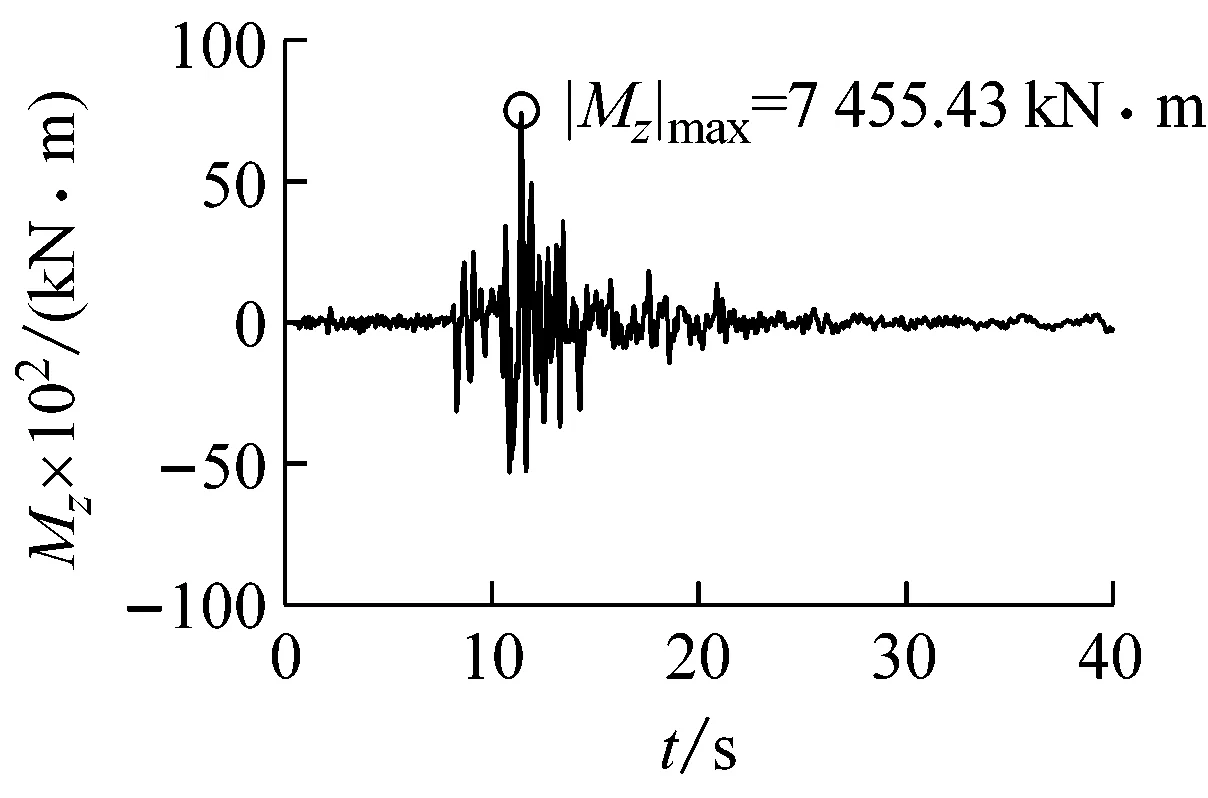
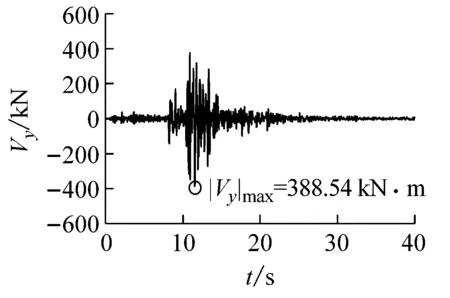
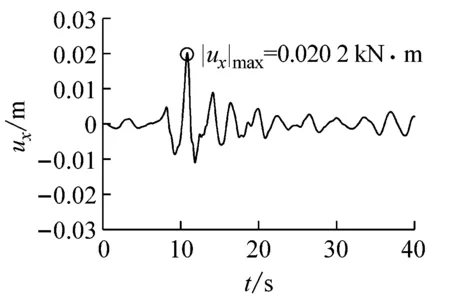
(e)隧道中点轴力图11 Loma Prieta波输入时隧道中点地震反应时程曲线Fig.11 Seismic response time-history curve of the tunnel midpoint subjected to Loma Prieta wave input

由表6可见，假定土层位移分布为正弦波式的规范方法计算结果与动力时程法相差过大。其中，位移值最大相对误差约为166%，弯矩值最大相对误差约为170%、剪力值最大相对误差约为20%，轴力值最大相对误差约为142%。可见，此时规范方法一计算精度较

表4 不同地震波作用下纵向整体式反应位移法计算结果

Tab.4 Results of the longitudinal integral response displacement method subjected to seismic-wave recordings

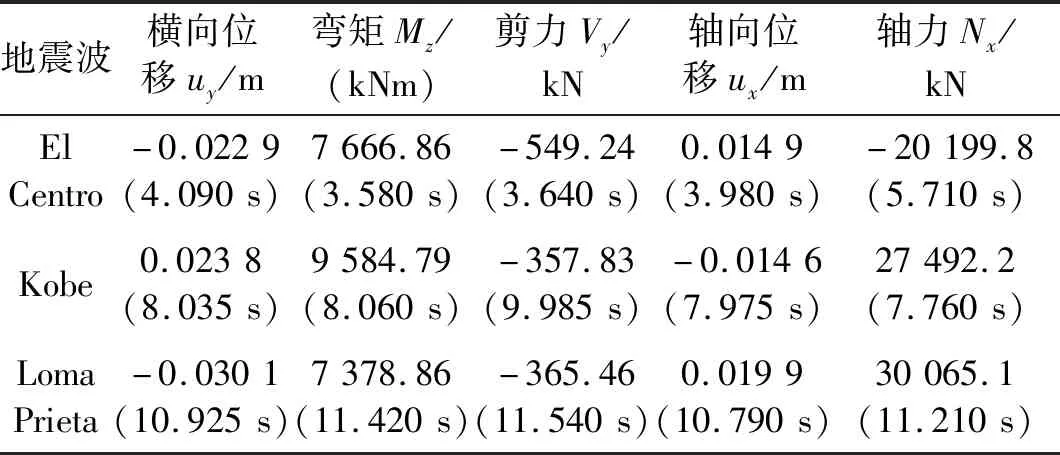
地震波横向位移uy/m弯矩Mz/(kNm)剪力Vy/kN轴向位移ux/m轴力Nx/kNElCentro-0.0229(4.090s)7666.86(3.580s)-549.24(3.640s)0.0149(3.980s)-20199.8(5.710s)Kobe0.0238(8.035s)9584.79(8.060s)-357.83(9.985s)-0.0146(7.975s)27492.2(7.760s)LomaPrieta-0.0301(10.925s)7378.86(11.420s)-365.46(11.540s)0.0199(10.790s)30065.1(11.210s)

表5 不同地震波作用下动力时程法计算结果

Tab.5 Calculation results of the dynamic time-history method subjected to different seismic-wave recordings

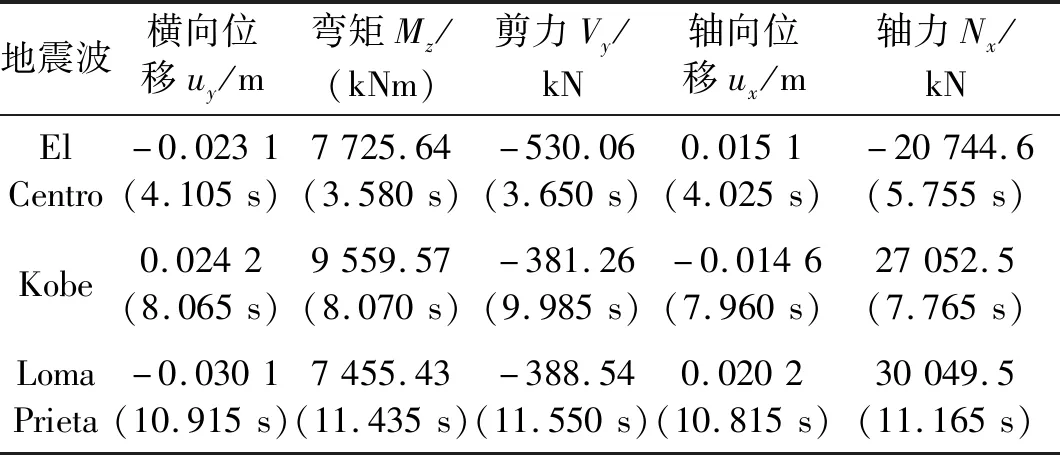
地震波横向位移uy/m弯矩Mz/(kNm)剪力Vy/kN轴向位移ux/m轴力Nx/kNElCentro-0.0231(4.105s)7725.64(3.580s)-530.06(3.650s)0.0151(4.025s)-20744.6(5.755s)Kobe0.0242(8.065s)9559.57(8.070s)-381.26(9.985s)-0.0146(7.960s)27052.5(7.765s)LomaPrieta-0.0301(10.915s)7455.43(11.435s)-388.54(11.550s)0.0202(10.815s)30049.5(11.165s)

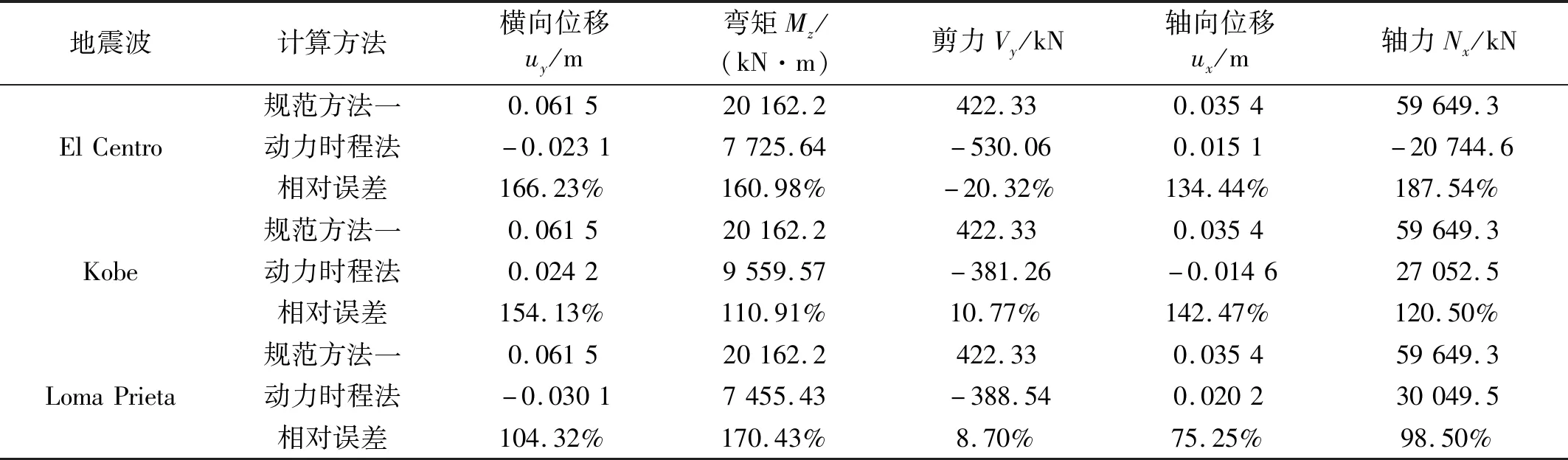
表6 不同地震波作用下规范方法一与动力时程法计算结果对比Tab.6 Results compared between the specification and the dynamic time-history methods subjected to seismic-wave recordings

表7 不同地震波作用下规范方法二与动力时程法计算结果对比Tab.7 Results compared between the specification and the dynamic time-history methods subjected to seismic-wave recordings

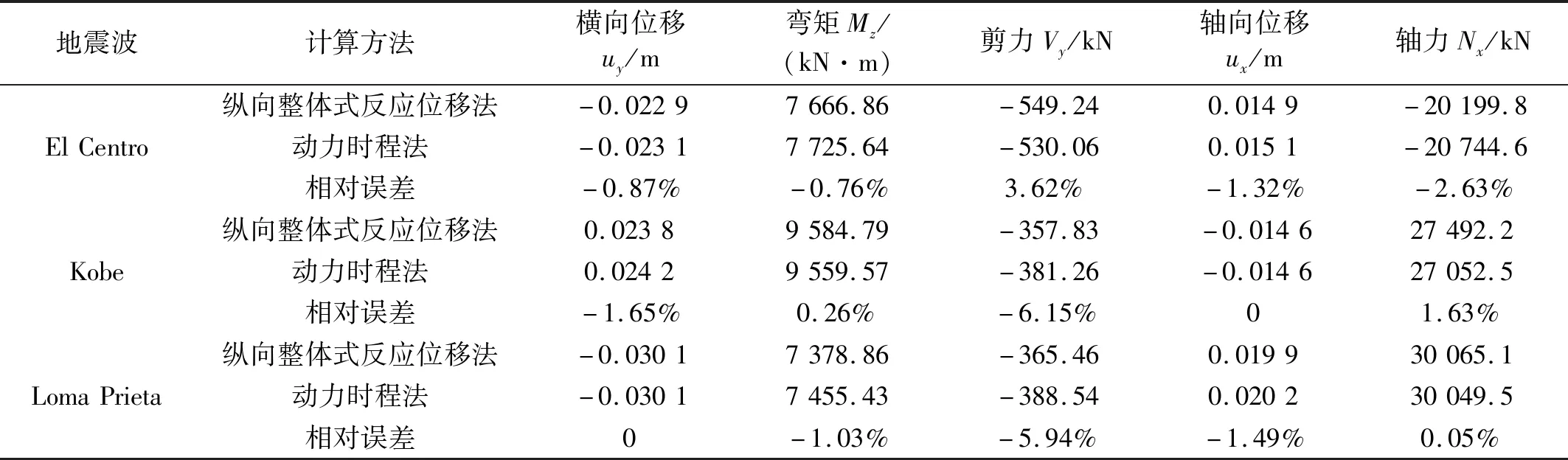
表8 不同地震波作用下纵向整体式反应位移法与动力时程法计算结果对比Tab.8 Results compared between the practical method and the dynamic time-history method subjected to seismic-wave recordings

低，过于简化了地震波斜入射时波动输入问题。

由表7可见，以自由场位移时程作为等效输入地震荷载的规范方法二得到的结构横向位移值与动力时程法较为接近、轴向位移值最大误差不超过7%，一定程度上反映了地下结构变形主要受到周围土层约束这一特点。该方法得到的结构弯矩最大相对误差约为3%，轴力最大相对误差约为30%，剪力最大相对误差达到约102%。以上计算误差是由结构-地基土弹簧计算模型带来的：离散的地基弹簧无法反映地基土层自身相互作用、不能准确模拟地基土对隧道结构的约束作用。另外，为获得隧道结构最不利地震反应，需要依次完成以各时间步自由场位移为等效地震作用的全部静力计算，过程较为繁琐。

由表8可见，纵向整体式反应位移法具有良好的计算精度，其计算结果与动力时程法较为接近：位移值(横向、轴向)相对误差不超过2%，弯矩值最大相对误差约为1%，剪力值最大相对误差约为6%，轴力值最大相对误差约为3%。

5 结 论

采用规范纵向反应位移法和纵向整体式反应位移法完成了SH波斜入射时北京某地铁区间盾构隧道结构的纵向地震反应分析，并与动力时程法计算结果进行了对比，主要结论如下。

(1)规范方法采用了结构-地基土弹簧模型，在一定程度上反映了地震作用下土体和结构之间的相互作用，但是离散的地基弹簧无法反映地基土层自身相互作用、不能全面的模拟真实土体的约束条件，带来格外的计算误差。另外，采用静力有限元法计算地基弹簧刚度系数时需要采用有限元模型完成多次计算，增加了工作量。

(2)将地震波作用下土层位移分布假定为正弦波形式的规范方法一，不能反映不同频谱成分地震波对隧道纵向地震反应的影响，此时得到的结构变形和内力与动力时程法均相差较大，不适合用于重要工程的地震反应分析。

(3)以自由场位移时程为等效地震作用的规范方法二，对于弯矩的计算精度良好，轴力的精度略差，而剪力的计算结果误差较大。该方法需要完成全部时间步下的静力计算才能确定结构最不利地震反应、影响了计算效率。

(4)纵向整体式反应位移法通过自由场运动简便的确定结构地震反应最不利时刻，使得实际地震波入射下结构最不利地震反应时刻的判断更易于操作。该方法通过直接建立地基土-隧道结构整体模型来反映土体-结构相互作用，对结构弯矩、剪力和轴力均具有良好的计算精度、计算效率较高。