基于OOMP与A-T谱的滚动轴承故障特征提取

夏均忠，郑建波，白云川，吕麒鹏，杨刚刚

(陆军军事交通学院 军用车辆工程系，天津 300161)

滚动轴承早期发生故障时产生的周期性脉冲特征微弱，又由于在信号监测和采集过程中不可避免混入噪声，导致滚动轴承故障诊断较为困难。如何在变转速下增强轴承故障特征信号，进而提取其故障特征一直是故障诊断领域的研究热点和难点。

为增强轴承故障特征，Wang等[1]提出了匹配追踪(Matching Pursuit,MP)的概念，McDonald等[2]提出正交匹配追踪(Orthogonal Matching Pursuit,OMP)方法。该方法存在两个主要缺点：过度匹配和非正交投影。在此研究基础上，论文提出优化正交匹配追踪(Optimized Orthogonal Matching Pursuit,OOMP)方法。针对OMP过度匹配问题，根据轴承故障振动信号的特性，设计一个组合时频原子字典与OMP进行匹配；针对非正交投影问题，引入鲸鱼优化算法(Whale Optimization Algorithm,WOA)选择与残余信号匹配的最优原子，实现信号重构和增强故障特征的目的。

为有效提取变转速下轴承故障特征，Antoni等[3]在循环平稳理论体系的基础上首次提出了角度/时间循环平稳(AngleTime Cyclostationary,AT-CS)理论，从全新的角度分析了变转速下旋转机械振动信号的角域周期性和频谱特性。Abboud等[4]在AT-CS的框架下提出了阶频谱相关(Order-frequency Spectral Correlation,OFSC)方法，成功提取了变转速下滚动轴承故障特征。在此研究基础上，论文引入角度-时间(Angular-temporal,A-T)谱方法[5]。A-T谱从循环平稳的角度分析了变转速下旋转机械振动信号固有特征，能够有效回避阶次跟踪的缺陷，解决变转速下轴承故障特征提取的问题。

1 优化正交匹配追踪(OOMP)

1.1 正交匹配追踪(OMP)

正交匹配追踪(OMP)原理是通过一个连续的迭代过程找到具有相对大的内积和残余信号的原子。设D={gγ(t)}γ∈Γ(Γ={γi,i=1,2,…})是希尔伯特空间H中的超完备字典，其中gγ是由参数组γ定义的字典原子。OMP算法的基本过程如图1所示。

(1)设置最大迭代次数m，把振动信号正交投影到原子字典D。

f=〈R0f,gγo〉gγo+R1f

(1)

式中，f为原始信号；gγo∈D；R1f表示残余信号。

然后，选择最佳匹配原子，即：

(2)

(2)通过Gram-Schmidt正交化方法将当前最佳匹配原子与先前原子正交。设u0=gγo，正交化过程表示如下

(3)

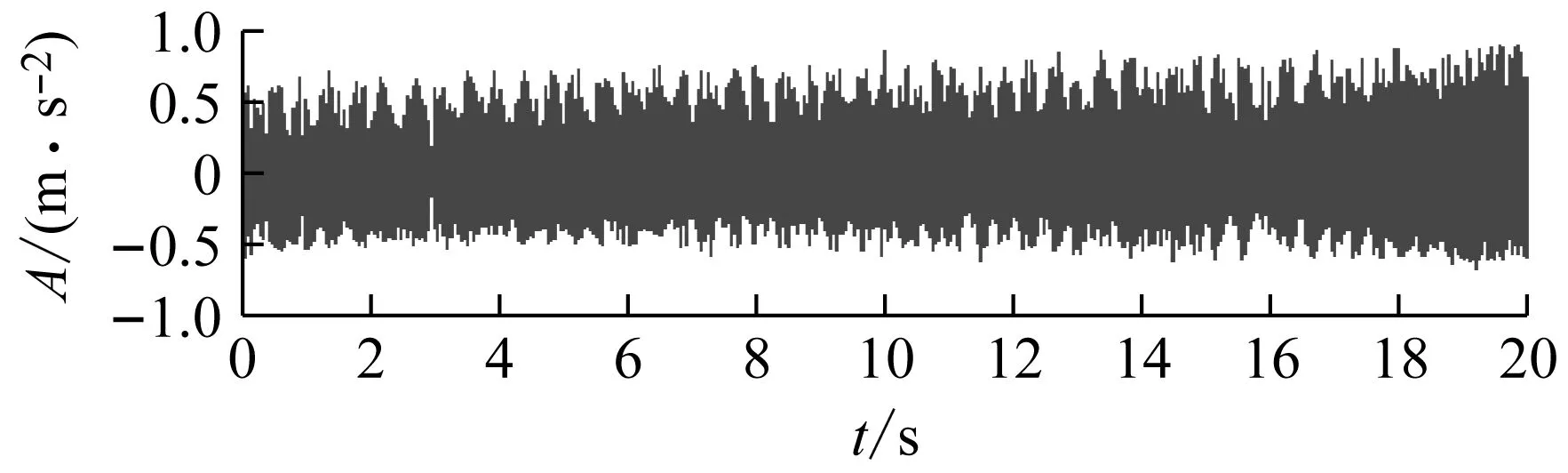
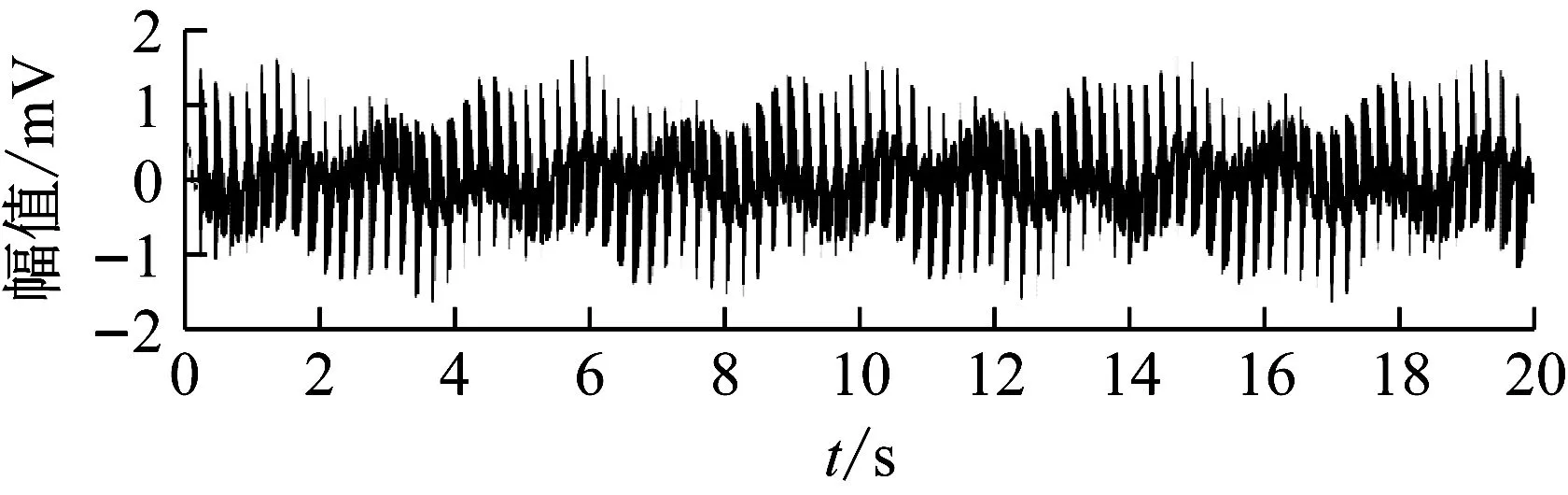
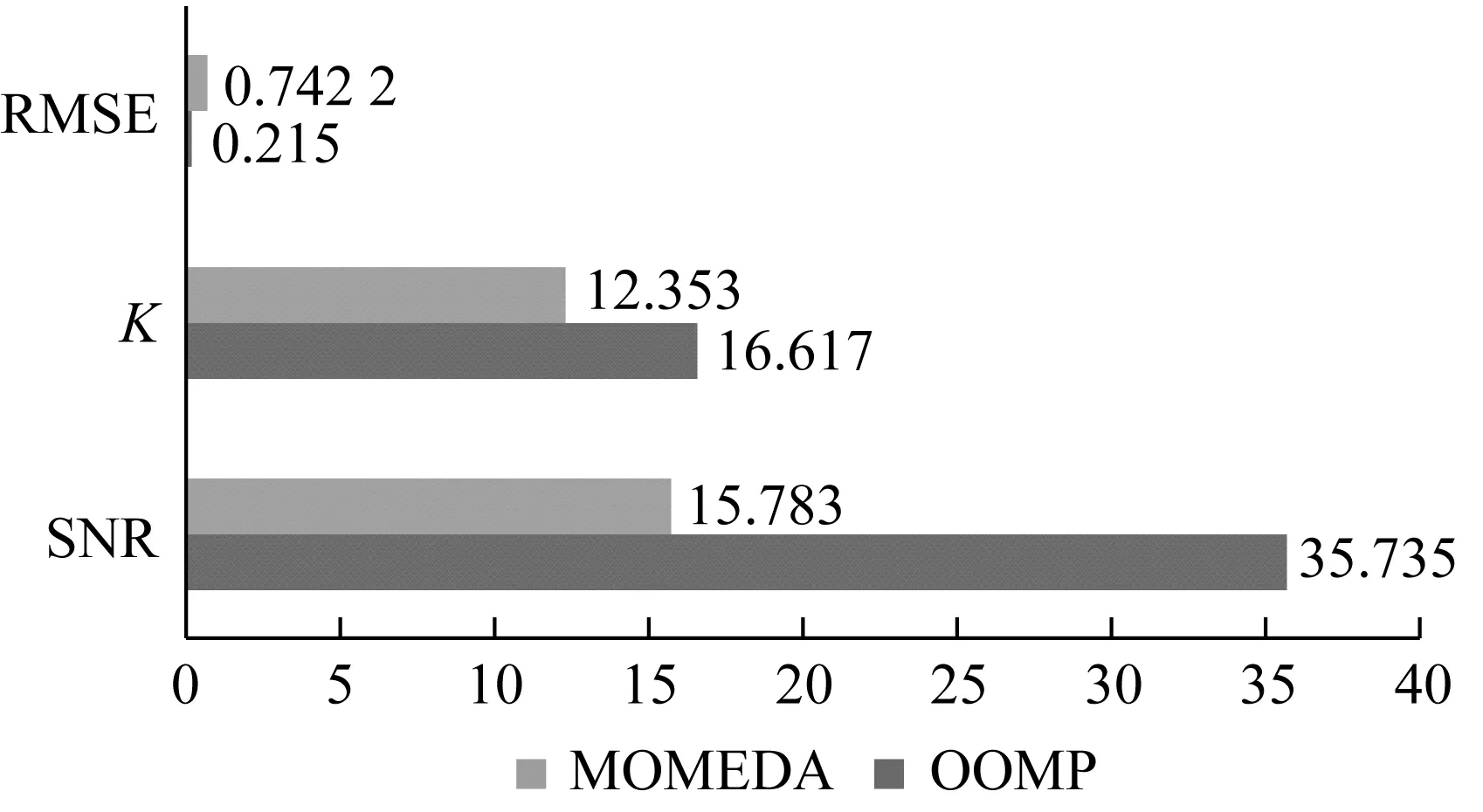
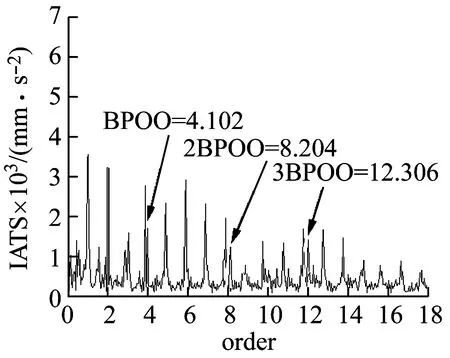
(3)计算当前n个原子在信号中的投影之和。若满足Rnf≠0和(Rnf，gγn)≠0，原子{gγk}0≤k

(4)

(4)重新计算残差信号Rnf。通过将残差信号Rnf投影到um上获得近似误差Rn+1f，即，

(5)

图1 OMP算法流程图Fig.1 Flow chart of OMP algorithm

1.2 优化正交匹配追踪(OOMP)

优化正交匹配追踪(OOMP)是在OMP方法的基础上更优的迭代算法：构建组合时频原子字典提高信号稀疏表示的准确性；运用WOA选择信号匹配的最佳原子。

(1)组合时频原子字典

选择构造字典的原子是信号稀疏表示的关键[6]。选择或构造的完备原子字典的原子数目应该与信号的采样点一样多。若原子数目不够，可能使信号由少量原子表示，造成结果较稀疏。滚动轴承振动信号主要由周期性正弦分量和冲击分量组成。原子傅立叶字典是一种正弦函数，随着时间的推移能很好地匹配信号的周期性正弦分量。此外，时频字典原子包含负指数函数，它很好地匹配故障特征。构造组合时频原子字典原子表达式如下

gγ=

(6)

式中，原子参数组是γ(s,p,u,ξ,θ)，s,p,u,ξ,θ分别是比例因子，阻尼系数，位移比例系数，频率因子和相位参数。

(2)鲸鱼优化算法(WOA)

为了消除OMP中非正交投影带来的冗余，在OMP迭代时引入鲸鱼优化算法(Whale Optimization Algorithm，WOA)。WOA算法是Aziz等[7]提出的一种搜索优化算法。该算法是模仿鲸鱼包围目标、搜寻目标、捕杀目标的行为来更新最佳位置。WOA首先假定当前为最佳搜索位置或接近于最佳。WOA更新位置公式如下

D=|CX*(t)-X(t)|

(7)

X(t+1)=X*(t)-AD

(8)

式中：A和C是优化系数；t代表当前的迭代次数；X(t)表示座头鲸当前位置向量；X*(t)表示座头鲸理想的位置向量。

式中，Tmax为最大迭代次数；r1和r2是[1,2]上的随机数。

由于鲸鱼在包围猎物的时候，按照螺旋式游向目标的同时还在收缩搜寻范围。收缩环绕与螺旋式前进的概率为50%。公式如下

X(t+1)=

(12)

鲸鱼在包围猎物的时候，会不断减小a的值，从而降低A值的范围。当A值的范围在[-1,1]时，A可为[-1,1]上的随机数。当A随机值大于1或小于-1时，意味着鲸鱼远离这一目标，重新搜索新的更合适的目标。这也展示了鲸鱼优化算法的全局搜索功能。为提高信号稀疏表示的效率和准确性，将WOA引入到OMP算法中选择与残余信号匹配的最优原子。

基于优化正交匹配追踪(OOMP)的滚动轴承故障脉冲增强算法流程如图2所示。

图2 基于OOMP故障特征增强流程图Fig.2 Flow chart based on OOMP noise reduction

步骤1获得原始信号。

步骤2根据原始信号，设置迭代次数，获取初始残差信号。确定相应参数，构造组合时频原子字典。

步骤3在迭代期间应用WOA，选择出与残余信号匹配的最优原子。

步骤4应用OOMP对原始信号进行重构。

传统上，开发智能系统的目标是追求一种理想的问题求解技术，这里的关键是我们需要解决的是什么样的问题。神经网路是用结构的复杂性而不是规则的复杂性来克服其处理问题的复杂性。让人工神经网络这一工具变得前所未有地强大的，正是其网络性而不是有关神经元的设想——因为神经元本身不管怎样复杂仍然是一个经典的输入输出系统。尽管如此，还是应该牢记一点，那就是神经网络主要是用来解决模式识别问题的。

2 角度-时间(A-T)谱

在OOMP增强故障特征信号的基础上，为了提取变转速下轴承故障特征，引入角度-时间(A-T)谱方法[8]。A-T谱在分析变转速下滚动轴承故障振动信号时，能够准确呈现信号幅值随频率阶次的变化规律，有效提取滚动轴承故障特征。其基本原理如下。

假设一变转速下振动信号为x(t)，对其进行标准化处理

(13)

其中

式中，φ0为初相位，Φ为角周期，T为最大时间周期，m为回转次数。其中

得到标准化后的信号zT(φ,t;φ0)，该过程简记为

x(t)→zT(φ,t;φ0)

(14)

式中，φ(t)为时间t对应的转角增量，φ0为初相位。

其次，对标准化后的信号进行傅里叶变换

(15)

最后，对ZT(φ,f;φ0)的平方包络进行傅里叶变换，得到信号x(t)的角度-时间(A-T)谱

AT ST(Ω,f;φ0)=

(16)

式中，f为时域中的频率(用Hz表示)，Ω为频率在角域的表示(即阶次)，θ为最大角度周期。

根据上述分析，基于OOMP与A-T谱的轴承故障特征提取流程为：

步骤1输入变转速下滚动轴承振动信号；

步骤2应用OOMP增强变转速下滚动轴承故障特征信号；

步骤3应用A-T谱提取滚动轴承故障特征。

3 试验验证

试验装置主要由变频器、驱动电机、负载滚筒、UC213滚动轴承、振动加速度传感器、转速传感器和信号采集系统等组成，如图3所示。

图3 试验装置示意图Fig.3 Schematic diagram of the test device

实验对象为东莞市TR轴承有限公司生产的UC213型滚动轴承，其主要技术参数见表1。

表1 UC213轴承主要技术参数Tab.1 The main parameters of bearing UC213

根据UC213轴承的相关技术参数，计算其外圈、内圈、滚动体的阶次理论值[9]分别为

使用电火花在轴承内圈、外圈、滚动体上加工直径Ф为0.5 mm，深度均为0.5 mm的圆坑，模拟点蚀故障。滚动轴承在变转速状态下运行，采集在电动机转速从12 000 r/min加速到15 000 r/min时滚动轴承的故障信号，采样时间为20 s，每种技术状态分别采集10组数据。轴承外圈故障振动信号和转速信号如图4所示。可以看出由于随机噪声及转速信号的存在，无法从时域信号发现故障信息。

图4 外圈故障转速曲线及其振动信号时域波形Fig.4 Outer cycle fault speed curve and its vibration signal time domain waveform

首先根据轴承故障振动信号的特性，使用OOMP方法增强轴承故障特征。根据原始信号特点，估计原子参数范围：s∈[1,N1]，p∈[0.01,1]，ξ∈[0,6 000]，θ∈[0,2π]，u=1，设置OOMP算法的迭代次数为340。构造的时频原子字典如图5所示。

运用OOMP对轴承振动信号进行处理后，其外圈时域信号如图6所示。对比图6与图4，可以发现OOMP处理后的故障脉冲信号相比于原始信号明显增强，同时去除了部分噪声干扰。由于篇幅所限，仅展示轴承外圈信号。

图5 时频原子字典Fig.5 Time-frequency atom dictionary

图6 OOMP处理后时域波形Fig.6 OOMP noise reduction time domain waveform

然后运用A-T谱提取OOMP处理后的轴承振动信号故障特征。A-T谱及其俯视图如图7(a)和(b)所示。由于三维A-T谱所包含的信息较多，较难从中发现轴承故障特征阶次和转频信息。通过三维A-T谱的俯视图只能辨别出其一倍故障特征阶次4.102。将三维A-T谱沿谱频率轴进行集成运算，得到信号在二维平面内的集成A-T谱[10]，如图7(c)所示。可以从集成A-T谱中清晰地识别出轴承外圈故障特征阶次4.102及其二倍及三倍阶次，诊断结果与试验相吻合。

(a)三维A-T谱

(b)三维A-T谱俯视图

(c)集成A-T谱图7 信号经OOMP处理后A-T谱图Fig.7 OOMP processed signal A-T spectrum

为对比分析，应用多点优化最小熵解卷积修正[11](Multipoint Optimal Minimum Entropy Deconvolution Adjusted,MOMEDA)。对图4外圈故障振动信号进行处理，其结果如图8所示。MOMEDA对轴承故障特征增强效果不如OOMP。

利用信噪比SNR、均方根误差RMSE和峭度K三个量化指标对这两种方法进行对比[12]，结果如图9所示。可以发现，较之MOMEDA，OOMP对于轴承故障特征增强效果比较理想。

图8 MOMEDA处理后时域波形Fig.8 MOMEDA noise reduction time domain waveform

图9 OOMP与MOMEDA效果对比Fig.9 OOMP and MOMEDA effect comparison

运用A-T谱提取MOMEDA处理后的轴承振动信号故障特征，三维A-T谱、及其俯视图和集成A-T谱如图10(a)、(b)和(c)所示。从图10(a)和(b)中只能辨别出少量转频，故障特征阶次模糊不清，而从图10(c)中发现其故障特征阶次不够明显，无法辨识出轴承故障模式。通过图7与图10对比，进一步证明了OOMP在变转速下轴承振动信号故障特征提取方面的优越性。

(a)三维A-T谱

(b)三维A-T谱俯视图

(c)集成A-T谱图10 信号经MOMEDA处理后A-T谱图Fig.10 MOMEDA processed signal A-T spectrum

4 结 论

论文提出一种基于OOMP和A-T谱的变转速工况下滚动轴承故障特征提取方法。通过构造组合时频原子字典和运用WOA对OMP中原子参数进行优化选择，实现了轴承故障脉冲增强；运用A-T谱提取信号的故障特征，实现了故障模式识别。变转速下轴承故障诊断试验证明了该方法的有效性和优越性。

(1)OOMP有效地解决了OMP存在的过度匹配和非正交投影的问题。通过与MOMEDA对比可知，OOMP能够更好地对故障特征进行增强。经过OOMP处理之后的重构信号在提取故障特征时具有更好地效果，使提取的故障特征信号更加准确。

(2)A-T谱在分析变转速下滚动轴承故障振动信号时，能够准确呈现信号幅值随频率阶次的变化规律。针对三维A-T谱表达信号特征不清晰的缺陷，通过集成运算将三维A-T谱转化为集成A-T谱，有效提取了轴承故障特征。

(3)将A-T谱与OOMP相结合，通过对故障特征信号的增强提高了故障特征提取准确度，同时有效地避免了阶次跟踪的缺陷，提高了故障模式识别和故障诊断的可靠性，是一种变转速下提取轴承故障特征的有效方法。