复合材料厚板多钉连接

(南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016)

1 引 言

在现代飞行器复合材料结构设计中，连接设计不可避免且是结构设计的关键环节。随着复合材料逐渐应用于主承力结构，需要连接的板更厚、钉径更大，连接区的受力也更为复杂。因此针对复合材料-金属厚板多钉连接强度问题展开研究，具有较高的理论意义和工程应用价值。

早先，由于复合材料板厚度较薄，国内外学者采用二维模型或平面解析方法。Dano等[1]利用二维模型对复合材料的损伤和应力情况进行分析，分析了不同失效准则对计算结果的影响。郑钰[2]针对复合材料薄板连接建立基于二维模型的失效判别软件，实现了同时运用多种失效准则对模型进行失效判定。但是随着板厚的增加，以上方法在针对复合材料厚板问题时会产生较大误差，所以学者们开始建立三维立体模型。Alfredo[3]提出一种二、三维混合模型来分析准各向同性板的开孔拉伸强度，在孔边采用三维建模，而在远离孔边区域采用了二维建模方式，节约了计算成本。Isaicu[4]采用了三维单元建模，根据结构对称的特点只建立了一半模型，在边缘处采用较粗的单元，在孔边则采用较细的单元进行建模。Gamble等[5]利用ABAQUS软件中连续壳单元进行建模，采用Hill破坏准则对包括分层在内的几种损伤扩展进行了预测，并预测复合材料板的极限载荷。

针对复合材料机械连接件的设计，学者们进行了多方面研究。Camanho等[6]通过ABAQUS建立三维有限元模型，讨论了预紧力和摩擦系数等因素对连接强度的影响。A Riccio等[7-8]对拉伸载荷下复合材料单剪螺栓连接损伤的起始和演化进行了试验研究，考察了钉头形式、螺栓直径和不同材料连接对结果的影响。刘兴科等[9]对复合材料—金属多钉连接的钉载分配进行了研究，讨论了各个因素对钉载分配的影响大小。同样是复合材料—金属螺栓连接，苏睿[10]建立了复合材料机械连接的疲劳累积损伤寿命预测方法，并讨论了配合方式等对结构疲劳寿命的影响。朱智毅[11]对复合材料厚板单钉连接进行研究，讨论了二维有限元建模和三维有限元的建模差异，并改进了Hart-Smith法中的应力集中因子C，使其能够应用于厚板领域。

本研究对复合材料厚板双钉单剪螺栓连接结构进行挤压强度试验，并对复合材料双钉单剪和双排四钉单剪螺栓连接结构建立三维渐进损伤有限元模型进行计算模拟，通过计算结果与试验结果对比，验证所建模型的正确性，并进一步讨论了复合材料厚度、摩擦系数、宽径比和孔距对复合材料厚板双钉单剪螺栓连接的连接刚度和挤压强度的影响，以及复合材料厚度因素与横向和纵向的孔距对复合材料厚板双排四钉单剪螺栓连接的连接刚度和挤压强度的影响。

2 厚板挤压强度试验

2.1 试件参数

试件材料采用T800S/BA9918典型铺层层压板，材料性能如表1所示。研究所采用的试件铺层为[45/0/-45/90/-45/45/0/45/-45/0]2s。试件共40层，每层的厚度均为0.19mm。螺栓采用凸头六角螺栓，材料为30CrMnSi，弹性模量E=206GPa，泊松比ν=0.3。与复合材料连接的为钢板，其弹性模量E=206GPa，泊松比ν=0.3。在试件的设计过程中为了避免出现拉断和剪短这种低强度的破坏模式，因此本试验的试件采用板宽-孔径比(W/D)=6，端距-孔径比(E/D)=3，图1为试件示意图。

其中，E11：层合板长度方向上的弹性模量；E22：层合板宽度方向上的弹性模量；E33：层合板厚度方向上的弹性模量；G12：面内两个方向上的剪切模量；G23和G13：两个层间剪切模量；ν12、ν23、ν13：泊松比；Xt：长度方向的拉伸；Xc：长度方向的压缩强度；Yt：宽度方向的拉伸；Yc：宽度方向的压缩强度；Zt：厚度方向的拉伸；Zc：厚度方向的压缩强度；S12、S23和S31：材料主轴方向的三个剪切强度参照ASTM D 5961/D 5961M-08标准在WDW-E300电子万能试验机(见图2)上进行静力拉伸试验。在试件螺栓孔附近安装标距为50mm的引伸计用来测量螺栓孔附近的挤压变形，并通过试验机自身的传感器来测量位移和载荷等数据。

图1 复合材料双钉单剪连接件的尺寸Fig.1 Dimensions of double-bolt, single-lap thick composite laminate

2.2 试验结果

图2 试验装置Fig.2 Test equipment

试验测出试件的位移载荷曲线和破坏载荷，通过计算得出其挤压强度，结果见表2。破坏形式均表现为挤压破坏，见图3。

表2 试验结果Table 2 Test result

图3 试件的破坏模式Fig.3 Failure modes of specimens

从图3可以发现，复合材料的孔边明显看出破坏痕迹，而金属板的孔边则不能看出破坏痕迹，这是因为金属的强度远大于复合材料的强度。

3 数值模拟

3.1 复合材料失效准则

影响复合材料强度的因素有铺层方式、加载方式和复合材料板的几何尺寸等因素。复合材料的失效过程十分复杂，本研究采用渐进损伤的方法来分析复合材料的失效过程。典型的渐进损伤一般分三个步骤：应力分析计算、失效判定和材料的退化。本研究主要采用三维Hashin准则[12]，材料退化选取Camanho刚度退化方案[13]。其中Hashin准则主要考虑了五种损伤形式即纤维拉伸破坏、纤维压缩破坏、基体拉伸破坏、基体压缩破坏和纤维基体剪切破坏。

(1)纤维拉伸破坏(σxx>0)

(1)

(2)纤维压缩破坏(σxx<0)

(2)

(3)基体拉伸破坏(σyy>0)

(3)

(4)基体压缩破坏(σyy<0)

(4)

(5)纤维基体剪切破坏(σxx<0)

(5)

(6)纤维基体剪切破坏(σxx>0)

(6)

其中：σii(i,j=x,y,z)分别表示复合材料各个方向上的主应力，σij(i,j=x,y,z)为对应面内的剪切应力。

3.2 刚度退化方法

复合材料失效分析有很多刚度退化准则，对于三维失效准则的退化，一般采用直接折减法，当材料判定失效后，采用对应的失效因子对刚度进行折减。本研究选择Camanho退化方案来进行刚度退化，Camanho退化模型见表3。

表3 Camanho退化模型Table 3 Camanho′s degradation model

当材料达到失效积分点时即可进行刚度折减，在实际计算中经常会有同一单元出现多种损伤失效模式，对于这种情况进行重复刚度折减。

3.3 渐进损伤分析过程

为了模拟复合材料厚板多钉螺栓连接结构在静力拉伸情况下的失效过程，本研究使用了VUMAT用户子程序来实现复合材料的失效判定和刚度退化。子程序内使用SDV状态变量来表示复合材料的损伤情况。当SDV<1的时候，单元还未达到损伤积分点，程序依然按照初始设定的材料参数进行计算。当SDV>1的时候，单元达到损伤积分点，按照失效准则，材料已经产生损伤，按选取的材料退化方案对材料参数进行刚度折减，程序按照新的材料参数重新进行计算。随着载荷的增大，失效的单元越来越多，当载荷足够大时，结构无法承载，载荷将不再增加，计算终止，认定复合材料最终失效。由此过程可以预测复合材料厚板多钉连接的强度，整个渐进损伤分析过程可用图4表示。

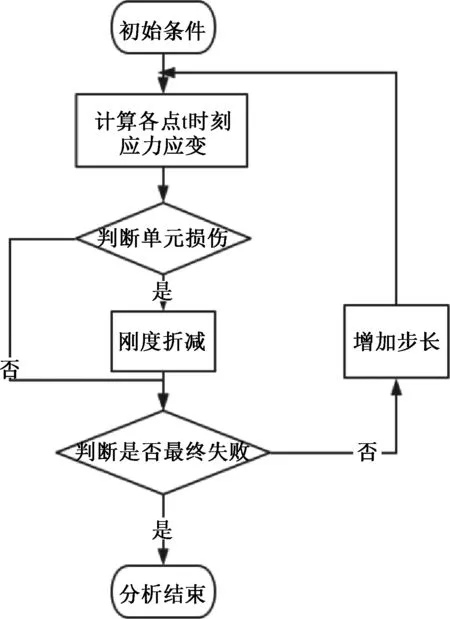
图4 分析过程Fig.4 Analytic process

使用ABAQUS软件[14]进行三维有限元分析，在软件中根据试件的材料参数和尺寸参数建立了三维有限元模型，编写了VUMAT用户子程序来定义材料的力学参数和描述复合材料的本构关系，通过子程序来实现复合材料的失效判定和刚度退化过程，由此来模拟复合材料厚板多钉连接结构在静力拉伸情况下失效过程，双钉单剪有限之模型如图5所示。将模型进行实体分割，沿厚度方向每一个铺层建立一个单元，模型中的复合材料板、金属板和螺栓均被划分为若干个三维八节点减缩积分单元即C3D8R单元。为减少计算量，在保证精度的前提下将复合材料板和金属板孔边单元划的较细而远离孔的单元则划的较为稀疏。采用了小滑移面面接触算法来模拟螺栓柱面与复合材料孔、螺栓柱面与金属孔，螺栓与螺母和复合材料和金属面的接触以及金属板与复合材料板的接触，在接触中加库伦摩擦来模拟接触产生的摩擦，选取的摩擦系数为0.15。模型一端采用固支的边界条件，另一端施加了一个沿X方向的位移加载方式来加载。

图5 双钉单剪有限元模型(左侧为2号钉，右侧为1号钉)Fig.5 Finite element model of double-bolt, single-lap thick composite laminate

4.1 计算结果和算例验证

本研究对复合材料厚板与金属混合连接双钉单剪试验件进行三维有限元建模和计算，通过渐进损伤计算得到模型的极限载荷为117.95kN，对应试验的载荷为122.12kN，误差为-3.41%。根据试验结果，试件的最终破坏形式为孔边压溃，图6是在破坏载荷下模拟试验件最终的破坏形式，其中深色区域为发生损伤的区域，可以看出损伤主要发生在孔边区域。

图6 模型最终破坏形式(左侧为1号钉，右侧为2号钉)Fig.6 Final failure form of model

当载荷到达一定程度时，复合材料板开始出现损伤，损伤随着载荷的增加而慢慢扩展，当损伤达到一定程度复合材料最终失效，结构无法继续承载。在ABAQUS中建立的三维有限元模型可以较好地模拟出复合材料厚板与金属多钉螺栓连接的渐进损伤过程。

因为试件是单剪，所以在靠近金属与复合材料的接触面的区域应力集中程度大于复合材料下表面的应力集中程度，所以本研究主要讨论靠近两板接触面的0°、45°、-45°和90°铺层的应力情况，图7为这四个铺层在破坏载荷下的应力云图。

通过观察应力云图可以发现每个铺层的应力方向分布大致与铺层角度相同，且两个钉的钉载分布规律也很明显，不论哪一个铺层靠近复合材料的2号钉的载荷和应力集中区域都是明显大于靠近金属的1号钉，说明了2号钉承载更多。

图8和图9分别是在承受60kN载荷和破坏载荷下的0°铺层钉孔附近应力分布云图。

比较60kN载荷下和破坏载荷下的钉载分布应力云图，可以看出1号钉和2号钉在60kN的载荷下承载差距较大，2号钉承担了更多的载荷，而载荷达到破坏时，两个螺栓承载差距有所缩小。这是由于随着载荷的增加，2号钉附近的复合材料损伤也慢慢扩大，接触面积也慢慢增大，应力集中程度降低，而1号钉损伤面积小能够承受更大的载荷，所以在破坏载荷下，两钉的承载差距缩小。

通过模拟还可以观察到渐进损伤的过程，本研究分别对纤维拉伸破坏、纤维压缩破坏、基体拉伸破坏、基体压缩破坏、纤维基体剪切破坏这五种典型的破坏模式进行分析。图10是靠近金属板的0°铺层在破坏载荷下的情况，深色部分为损伤产生的区域。

在加载过程中无论是哪个铺层的哪种损伤，总是2号钉附近的复合材料最先发生，而且随着载荷的增加2号钉附近的损伤区域也大于1号钉，当载荷快达到破坏载荷时，1号钉附近的损伤区域大小开始接近2号钉。这个结果也与之前钉载分配的结论相同，这说明2号钉的承载大于1号钉，虽然随着载荷的变化，承担的载荷比例会发生一些变化，但是总体上2号钉所承担的载荷和损伤区域都大于1号钉。

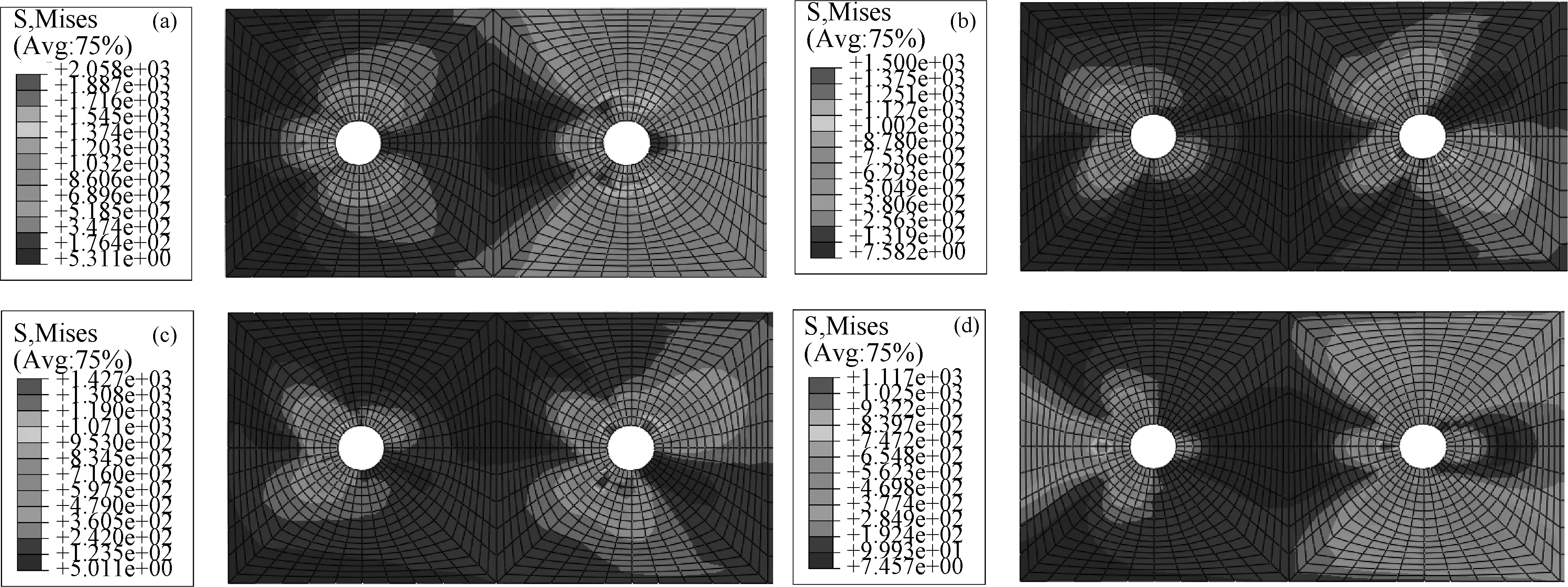
图7 在破坏载荷下复合材料各角度铺层应力分析 (a) 0°铺层应力； (b) 45°铺层应力； (c) -45°铺层应力； (d) 90°铺层应力Fig.7 Stress analysis of composite material at different angles under failure load(a) Stress of 0° ply; (b) Stress of 45° ply; (c) Stress of -45° ply; (d) Stress of 90° ply

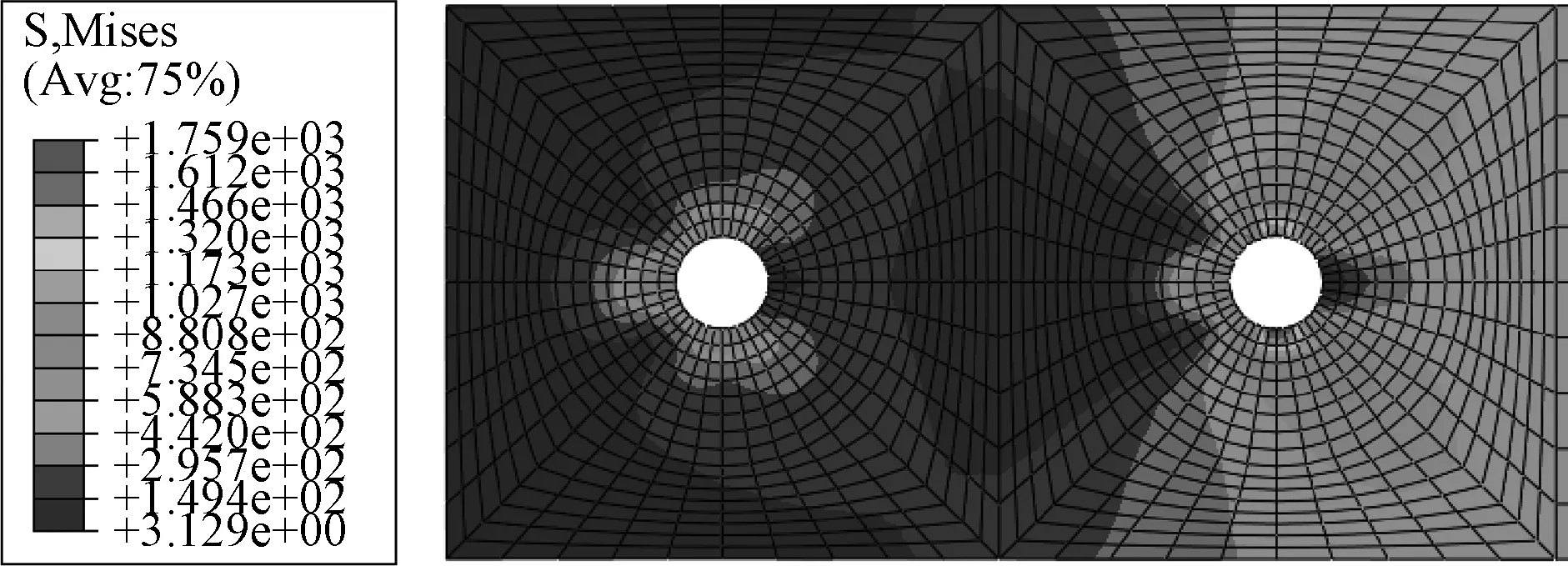
图8 60kN载荷下钉载分布Fig.8 Load distribution under 60kN

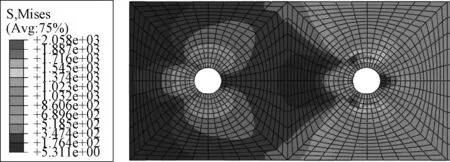
图9 破坏载荷下的钉载分布Fig.9 Load distribution under failure load

图10 0°铺层的损伤情况 (a) 纤维拉伸破坏；
(b) 纤维压缩破坏； (c) 基体拉伸破坏；
(d) 基体压缩破坏；(e) 纤基剪切破坏
Fig.10 Damage on the 0° ply (a) fiber tensile;
(b) fiber compressive; (c) matrix tensile;
(d) matrix compressive; (e) fiber-matrix shear

4.2 网格密度对双钉单剪连接计算结果的影响

通过改变孔边单元数量，来研究三维有限元模型的网格密度对计算结果的影响，选取合适的网格密度进行建模计算，所用的材料参数、尺寸均参照第2.1节的试件参数。分别选取孔边单元数为24、32、40、48和56来进行建模计算，每一个孔边单元的横向与纵向尺寸比值均近似于1∶1，计算结果如表4所示。图11为不同网格密度的有限元模型的计算结果与试验结果的比较。综合图、表可以发现，计算结果与试验结果的误差均在10%以内，而且计算结果随着网格越来越密而越来越趋近于试验结果。综合考虑为了节省计算成本，最终选取孔边单元数40来进行计算分析。

表4 不同的网格密度下结构的极限载荷Table 4 Failure load under different mesh density

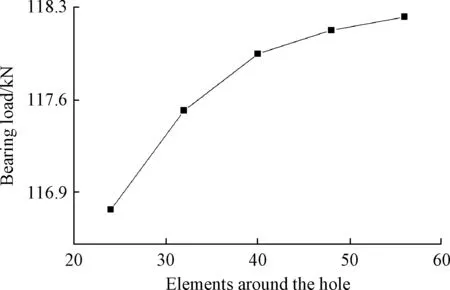
图11 不同网格密度对应的极限载荷Fig.11 Failure load under different mesh density

4.3 厚度对双钉单剪连接强度的影响

为了研究厚度因素对复合材料双钉单剪连接强度的影响，对除铺层数外，其他尺寸、参数均与试件相同的复合材料板进行分析，每一层铺层厚度均为0.19mm。共对四种厚度的复合材料板进行三维有限元分析，每一个模型各个角度铺层比例相同，铺层分别为[45/0～45/90]2S，[45/0～45/90]3S，[45/0～45/90]4S，[45/0～45/90]5S，厚度分别为3.04、4.56、6.08和7.6mm。表5为四种厚度的双钉单剪的模拟极限载荷和模拟连接强度，图12为连接强度随厚度变化的曲线图。综合图、表发现，复合材料的极限载荷随着厚度的增加而增加，厚径比为0.76的复合材料板的极限载荷是厚径比为0.304的复合材料板的两倍多，而连接强度却随着厚度的增加而降低。

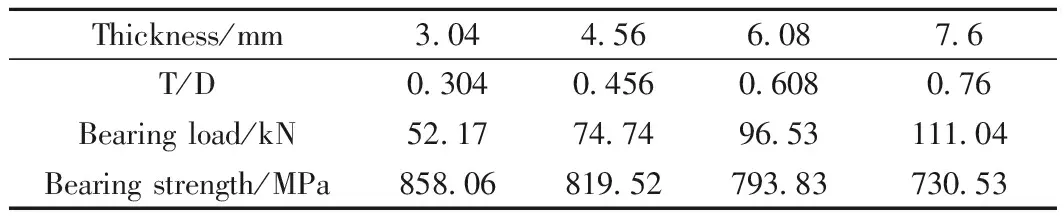
表5 各个厚度下的双钉单剪结构的极限载荷和连接强度Table 5 Failure load and connection stiffness of double-bolt, single-lap thick composite laminate under different thickness

图12 连接强度随厚径比变化趋势Fig.12 Curve of connection stiffness with thickness ratio

4.4 厚度对双钉单剪连接钉载分配的影响

按照理论分析，双钉单剪结构的两钉所承受的载荷应大小相等，但是根据上文分析可以发现，两钉所承受的载荷是不一样，2号钉所承受的载荷明显大于1号钉，为了研究厚度因素对双钉单剪结构钉载分配的影响，分别对第4.3节所建立的四种厚度的双钉单剪结构的两个螺栓所承受的载荷进行计算，结果见表6。通过两钉承载占总载荷的比例可以发现，随着厚度的增加，2号钉所承受的载荷总是大于1号钉，但两钉的承载差距越来越小，这是由于双钉单剪的钉载差距主要由于加载端与固定端不在同一条直线上，加载时会产生偏心效应，层合板出现二次弯曲现象(如图13)而产生，当复合材料板和金属板的厚度增加时，二次弯曲现象减轻，所以钉载分配更为均匀。

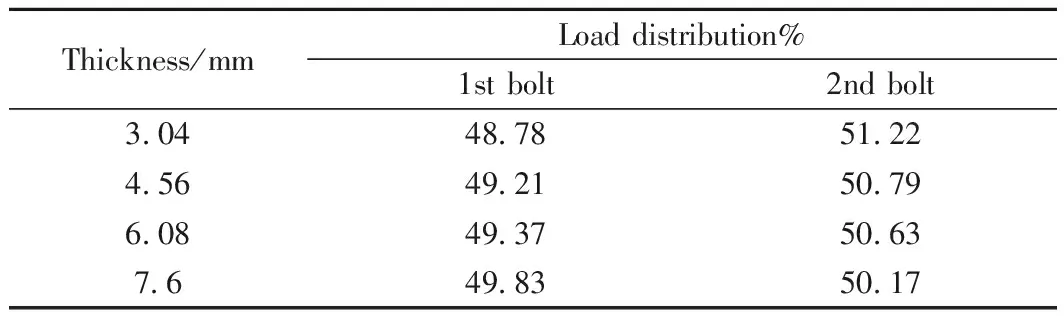
表6 双钉单剪在不同厚度下钉载分配Table 6 Load distribution of double-bolt, single-lap thick composite laminate under different thickness

图13 双钉单剪结构二次弯曲现象Fig.13 Sub-bending of double-bolt, single-lap thick composite laminate

4.5 厚度对双钉单剪连接破坏模式的影响

随着载荷的增加，复合材料板所受的载荷达到一定程度后会产生损伤，并且损伤会按照一定的规律扩展，由于复合材料板靠近金属板的铺层所承受的载荷最大，因此本研究只分析两板接触面的铺层的破坏情况。表7表示了不同厚度4个角度的铺层最先出现破坏的位置和破坏模式。从表可见，破坏发生的位置与铺层角度一致且都出现在2号钉附近，这与图8、图9分析钉载分配的结果一致。除了0°层，其他角度铺层最先出现的破坏模式都是基体拉伸破坏，可以看出厚度因素对复合材料破坏模式的影响不大。

4.6 摩擦系数对结果的影响

利用所建立的三维有限元模型，分别将金属板与复合材料板之间的摩擦系数设为0.15、0.2、0.3、0.4和0.5，计算结果如表8所示。从表可见，当摩擦系数为0.5的时候连接强度最大，说明适当的增加金属板与复合材料板之间的摩擦系数可以在一定程度上增加复合材料的连接强度。图14是复合材料与金属双钉连接的连接强度随摩擦系数的变化趋势图。从图可见，连接强度随着摩擦系数的增加而增大，但是增长幅度逐渐降低。因为复合材料与金属之间的接触比较复杂，所以增长趋势并不是线性的，而且由于增长幅度不大，对整体连接强度的影响也不大。

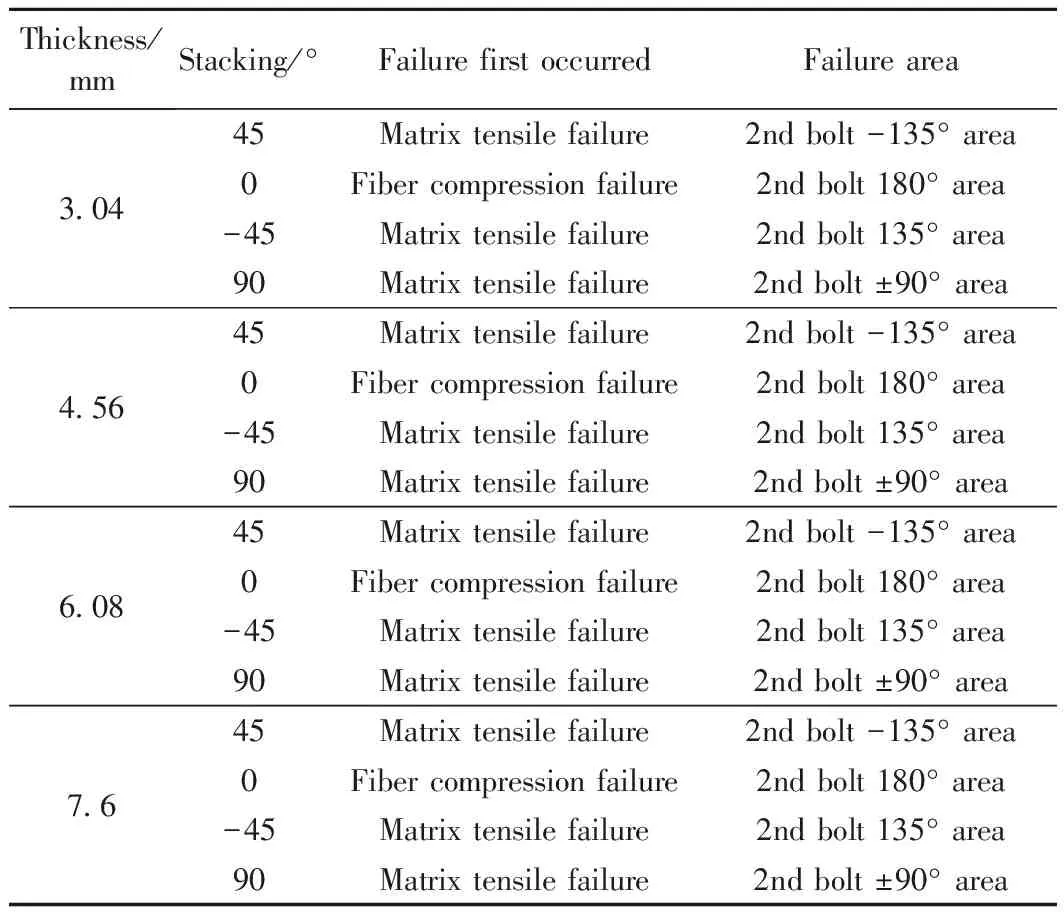
表7 不同厚度下复合材料各角度铺层破坏模式Table 7 Failure modes of composite material plies under different thickness

表8 各摩擦系数下的连接强度Table 8 Connection stiffness under different friction coefficients

图14 连接强度随摩擦系数变化趋势Fig.14 Curve of connection stiffness with friction coefficient

4.7 宽径比对结果的影响

分别选取宽径比为5、6、7、8这四种情况进行有限元建模计算来研究宽径比对连接强度的影响。只改变模型的宽度，材料、端距、孔径和长度均与验证模型相同。各宽径比所对应的连接强度如表9所示，连接强度随宽径比的变化趋势如图15所示。综合图、表可以看出，随着宽径比的增加，连接强度刚开始增加明显，宽径比为6连接件的连接强度为117.95kN，而宽径比为5连接件的连接强度为106.22kN，连接强度增加了10.17%，可以看出，增大宽径比对改善结构的连接强度有明显效果。但当宽径比大于6后，连接强度随宽径比的增加趋势减缓，而且增加宽径比也会造成材料的增加和结构质量的增加，对提高结构承载力帮助不大。

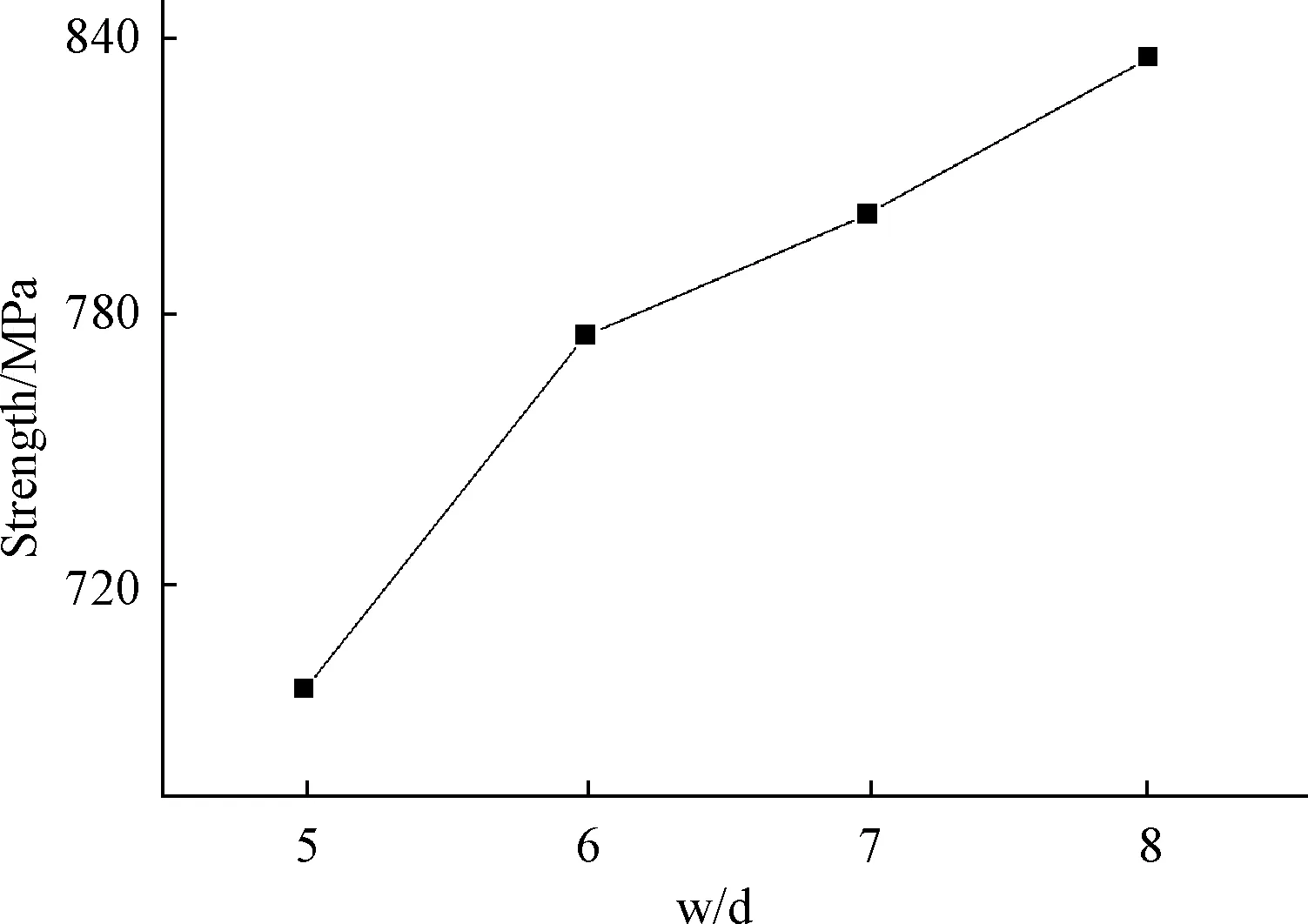
图15 连接强度随宽径比的变化Fig.15 Curve of connection stiffness with w/d

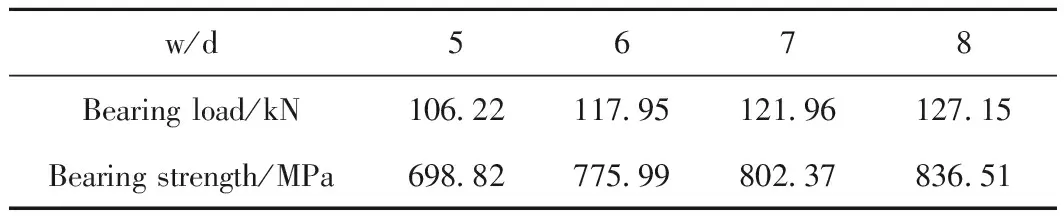
w/d5678Bearing load/kN106.22117.95121.96127.15Bearing strength/MPa698.82775.99802.37836.51

4.8 孔距对连接强度的影响

分别选取孔距为50、60、70和80mm四组孔距进行有限元建模计算来模拟孔距对复合材料连接件连接强度的影响。只通过改变2号钉的位置来调整孔距，而材料、1号钉的端距、试验件的长度均与验证算例相同。不同的孔距所对应的连接强度如表10所示，图16为复合材料-金属双钉单剪连接连接件的连接强度随孔距的变化趋势图。当孔距为80cm时，连接件连接强度最大比孔距为50的连接件的连接强度增加了8.43%，且连接强度随着孔距的增加而增大，可以看出增大孔距可以在一定程度上改善结构的连接强度，但是孔距的增大会造成结构尺寸和结构质量的增加，特别是在两钉以上的情况。

表10 不同孔距对应的连接强度Table 10 Connection stiffness under different hole pitches

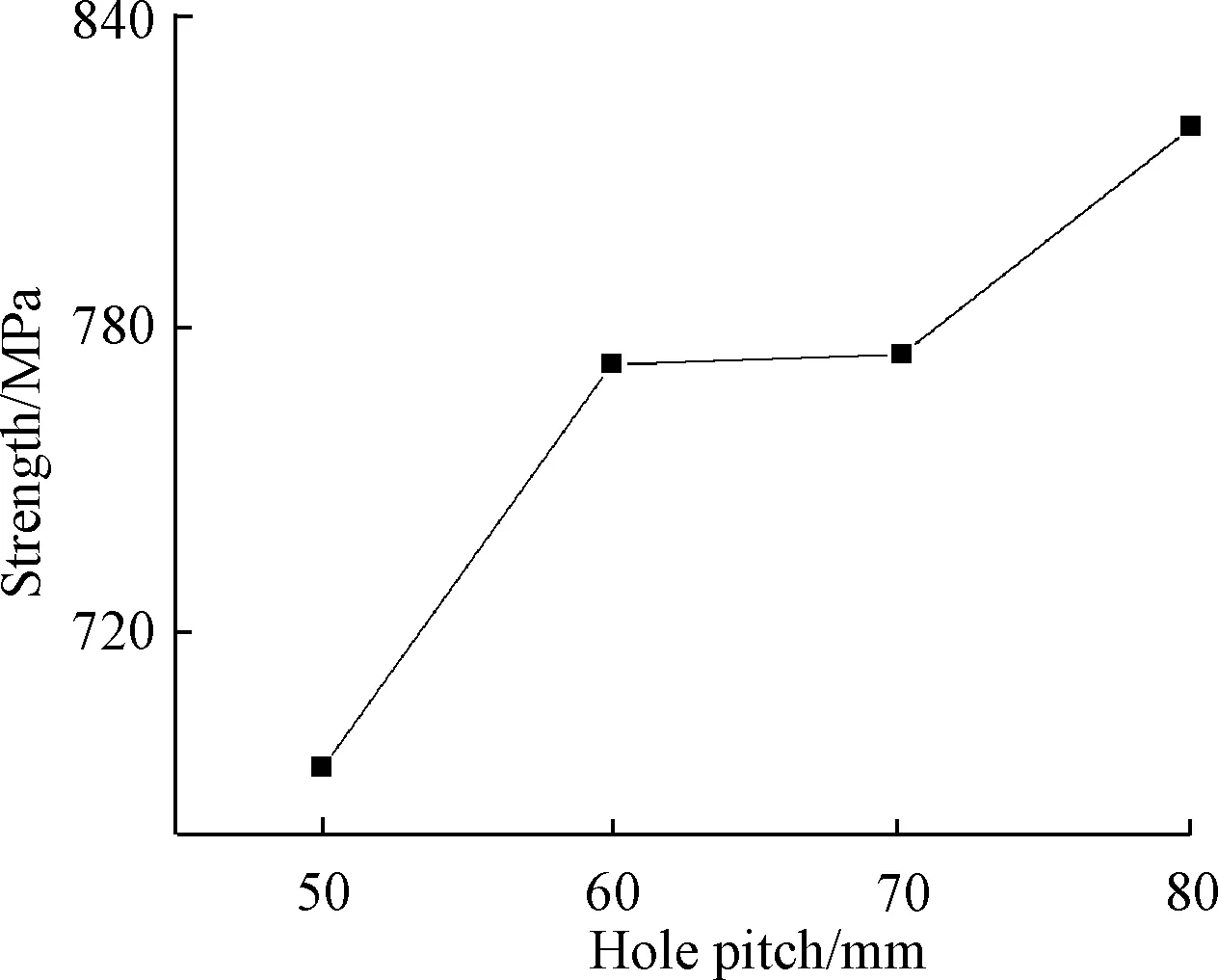
图16 连接强度随孔距的变化Fig.16 Curve of connection stiffness with hole pitches

为了进一步研究复合材料—金属多钉连接，对复合材料—金属双排四钉单剪连接进行了研究。T800S/BA9918层合板铺层方式为[45/0/-45/90/-45/45/0/45/-45/0]2s，单层厚度0.19mm，共40层，总厚度7.6mm。金属材料30CrMnSi的性能参数见表11，结构的几何尺寸见图17。

表11 金属材料的性能参数Table 11 Mechanical properties of metallic material

图17 复合材料多钉单剪连接件尺寸(左下角为1号钉，右下角为2号钉，右上角为3号钉，左上角为4号钉)Fig.17 Dimensions of multiple-bolt, single-lap thick composite laminate

基于ABAQUS有限元模型对图17的结构进行三维有限元计算，建立的模型如图18所示。对实体采用分割技术来进行建模，沿厚度方向每一个铺层建立一个单元，模型中的复合材料板、金属板和螺栓均被划分为若干个三维八节点减缩积分单元即C3D8R单元。为了节省计算时间，在保证精度的前提下将复合材料板和金属板孔边单元划的较细而远离孔的单元则划的较为稀疏。采用了小滑移面面接触的算法来模拟螺栓柱面与复合材料孔、螺栓柱面与金属孔，螺栓与螺母和复合材料和金属面的接触以及金属板与复合材料板的接触，在接触中加了库伦摩擦来模拟接触产生的摩擦，选取摩擦系数为0.15。模型一端采用固支的边界条件，另一端施加了一个沿X方向的位移加载方式来加载。

图18 多钉单剪有限元模型(左板为金属板，右板为复合材料板)Fig.18 Finite element model of multiple-bolt, single-lap thick composite laminate

和双钉单剪相同，四钉单剪也是在最接近两板接触面的45°、0°、-45°和90°铺层应力集中最为严重，所以只选取靠近两板接触面的4个铺层来讨论，图19为在破坏载荷下各铺层的应力云图。

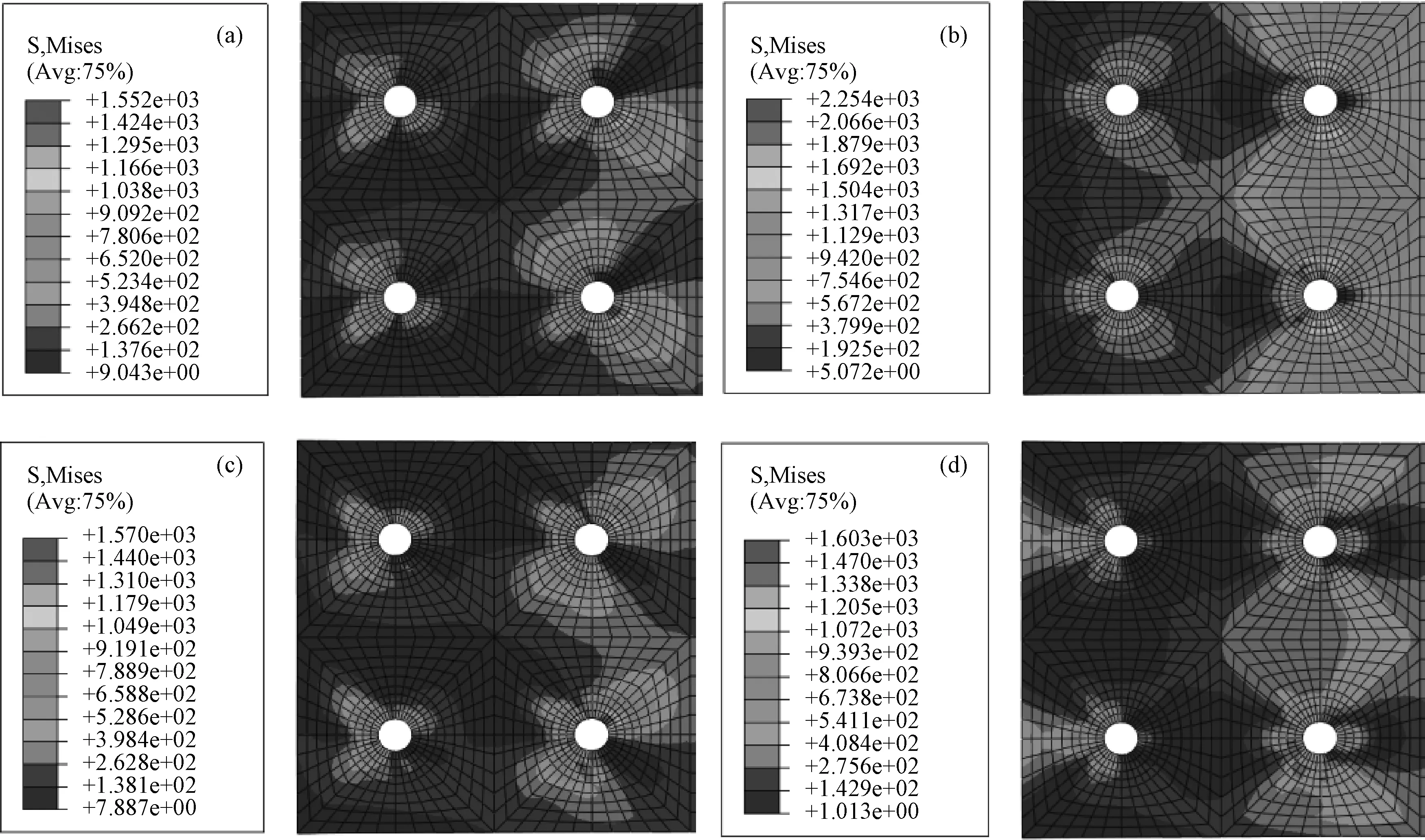
图19 复合材料各角度铺层在破坏载荷下应力云图 (a) 45°； (b) 0°； (c) -45°； (d) 90°Fig.19 Stress analysis of composite material at different angles under failure load ply (a) 45°; (b) 0°; (c) -45°; (d) 90°

从图可见，每个铺层的应力方向分布大致与铺层角度相同，且四个钉的钉载分布规律也很明显，不论哪一个铺层靠近复合材料的2号钉和3号钉的载荷和应力集中区域都是明显大于靠近金属的1号钉和4号钉，说明2号钉和3号钉承载更多。

图20和图21分别是在150kN和破坏载荷下0°铺层应力云图。观察钉孔附近的应力差异可以看出，1号钉和4号钉承担的载荷明显小于2号钉和3号钉。当载荷为150kN时，1号钉和4号钉承担载荷与2号钉和3号钉差距较大，但当达到破坏载荷后差距逐渐缩小，这是因为随着载荷的增加，2号钉和3号钉附近的损伤区域不断扩展，接触面积增大，而1号钉和4号钉损伤面积小，承载能力强，所以在破坏载荷下承载比例增加。当载荷为150kN时，3号钉的载荷略大于2号钉，而当载荷达到破坏载荷的时候，2号钉的载荷又略大于3号钉，但钉载差距明显小于前排螺栓的钉载差距。

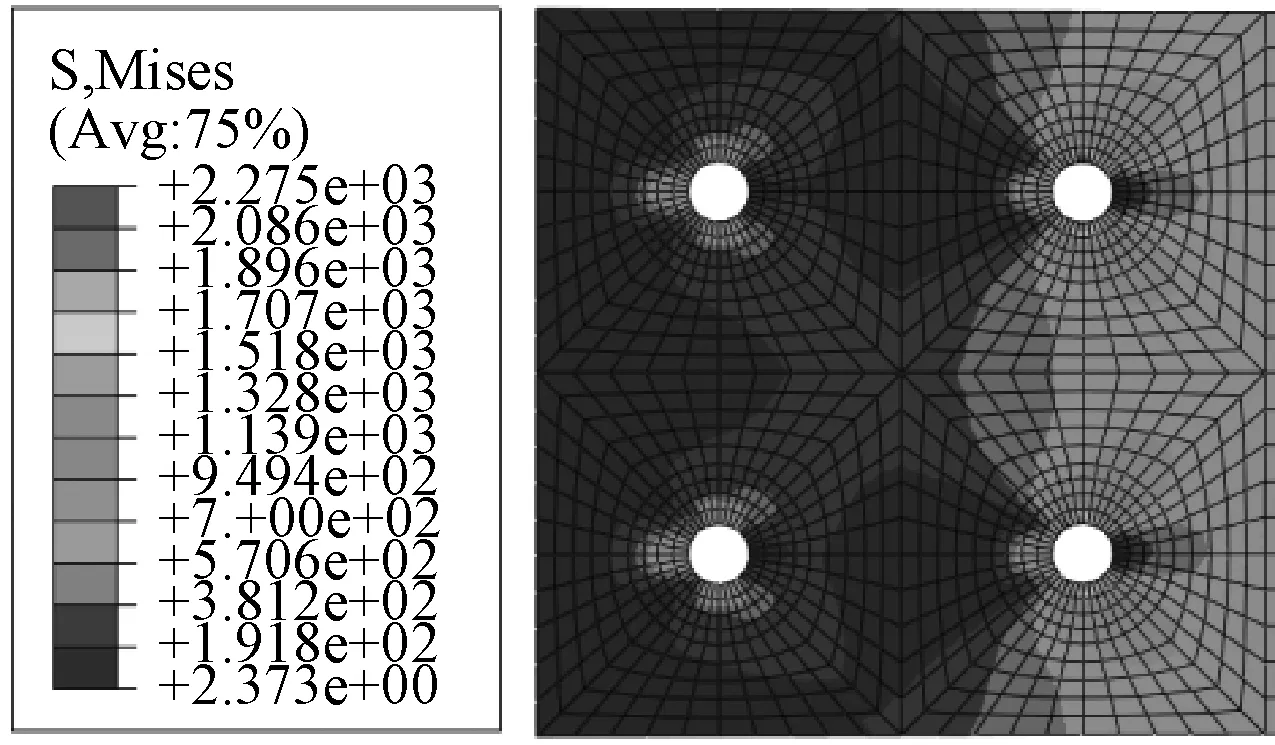
图20 载荷为150kN时钉载分布Fig.20 Load distribution under 150kN

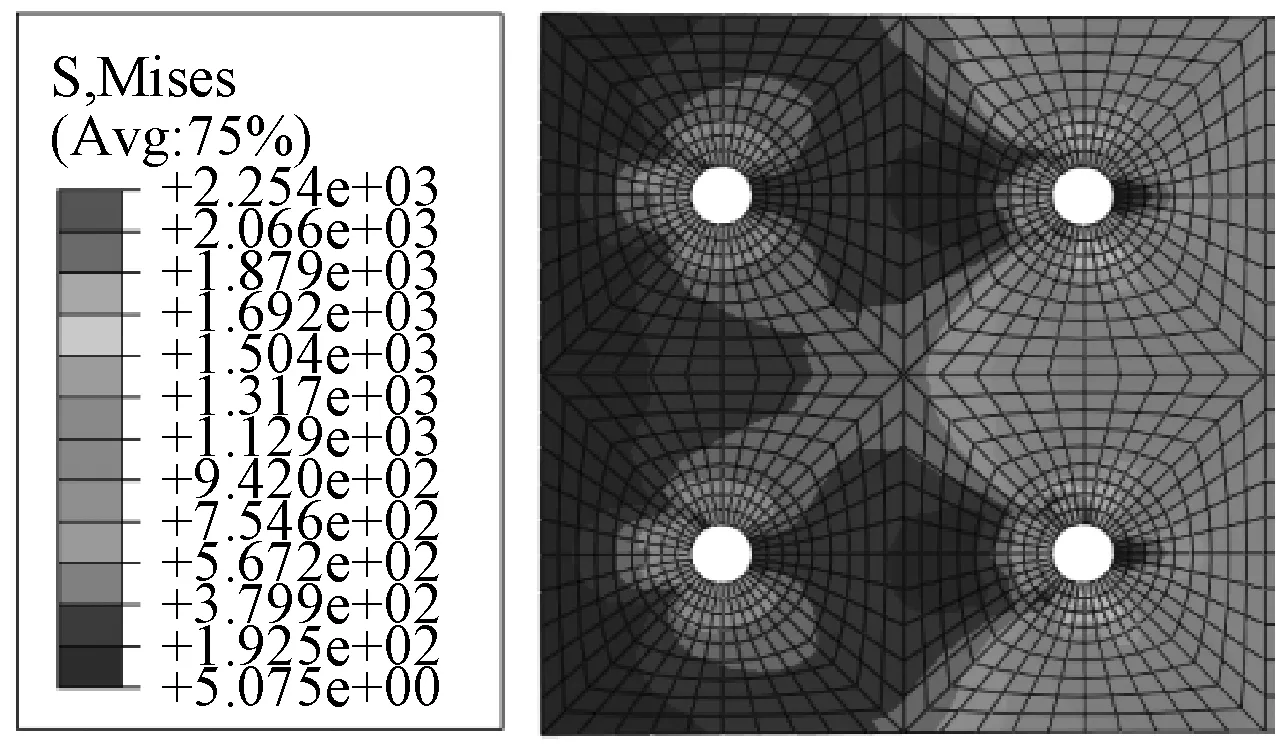
图21 载荷为破坏载荷时钉载分布Fig.21 Load distribution under failure load

与双钉单剪一样，四钉单剪的损伤扩展研究也针对纤维拉伸破坏、纤维挤压破坏、基体拉伸破坏、基体挤压破坏和纤基剪切破坏这五种形式进行。选取靠近两板接触面的0°层研究损伤扩展，破坏形式如图22所示。

从图可见，无论哪一种损伤形式，2号钉和3号钉附近的损伤区域都大于1号钉和4号钉，这与之前分析的钉载分配结论相一致，说明在加载时2号钉和3号钉承担的载荷要大于1号钉和4号钉。

图22 0°铺层损伤形式 (a) 纤维拉伸破坏；
(b) 纤维压缩破坏； (c) 基体拉伸破坏；
(d) 基体压缩破坏； (e) 纤基剪切破坏
Fig.22 Damage on the 0° ply (a) fiber tensile;
(b) fiber compressive; (c) matrix tensile;
(d) matrix compressive; (e) fiber-matrix shear

5.1 厚度对连接强度的影响

为研究厚度因素对复合材料多钉连接的连接强度影响，对厚度分别为3.04、4.56、6.08和7.6mm的复合材料板进行三维有限元分析，每一层铺层厚度均为0.19 mm，其他的参数、尺寸均与试件相同。每一个模型各个角度铺层的比例相同，铺层分别为[45/0～45/90]2S，[45/0～45/90]3S，[45/0～45/90]4S和[45/0～45/90]5S。表12是四种厚度的多钉单剪的模拟极限载荷和模拟连接强度，图23为连接强度随厚度的变化曲线。和双钉单剪一样，复合材料的极限载荷随着厚度的增加而增加，厚径比为0.76的复合材料板的极限载荷是厚径比为0.304的两倍多，但连接强度却随着厚度的增加而降低。

5.2 厚度对多钉单剪连接钉载分配的影响

根据理论分析，本研究所选的多钉单剪结构的四个螺栓所承受的载荷应大小相等，但根据分析可知复合材料厚板双钉单剪的两钉所承受的载荷不同，2号钉和3号钉所承受的载荷明显大于1号钉和4号钉。为研究厚度因素对多钉单剪结构钉载分配的影响，分别对所建立的4个厚度的多钉单剪结构的两个螺栓所承受的载荷进行计算，结果见表13。通过四钉承载占总载荷的比例可以发现，随着厚度的增加，2号钉和3号钉所承受的载荷总是大于1号钉和4号钉，但两排钉的承载差距越来越小，这也是由于加载时会产生偏心的效应，当复合材料板和金属板的厚度增加时，二次弯曲现象减轻，所以钉载分配更为均匀。而1号钉和4号钉、2号钉和3号钉有板宽较宽，也有微小的承载差距，但横向钉载差距明显小于纵向钉载差距。

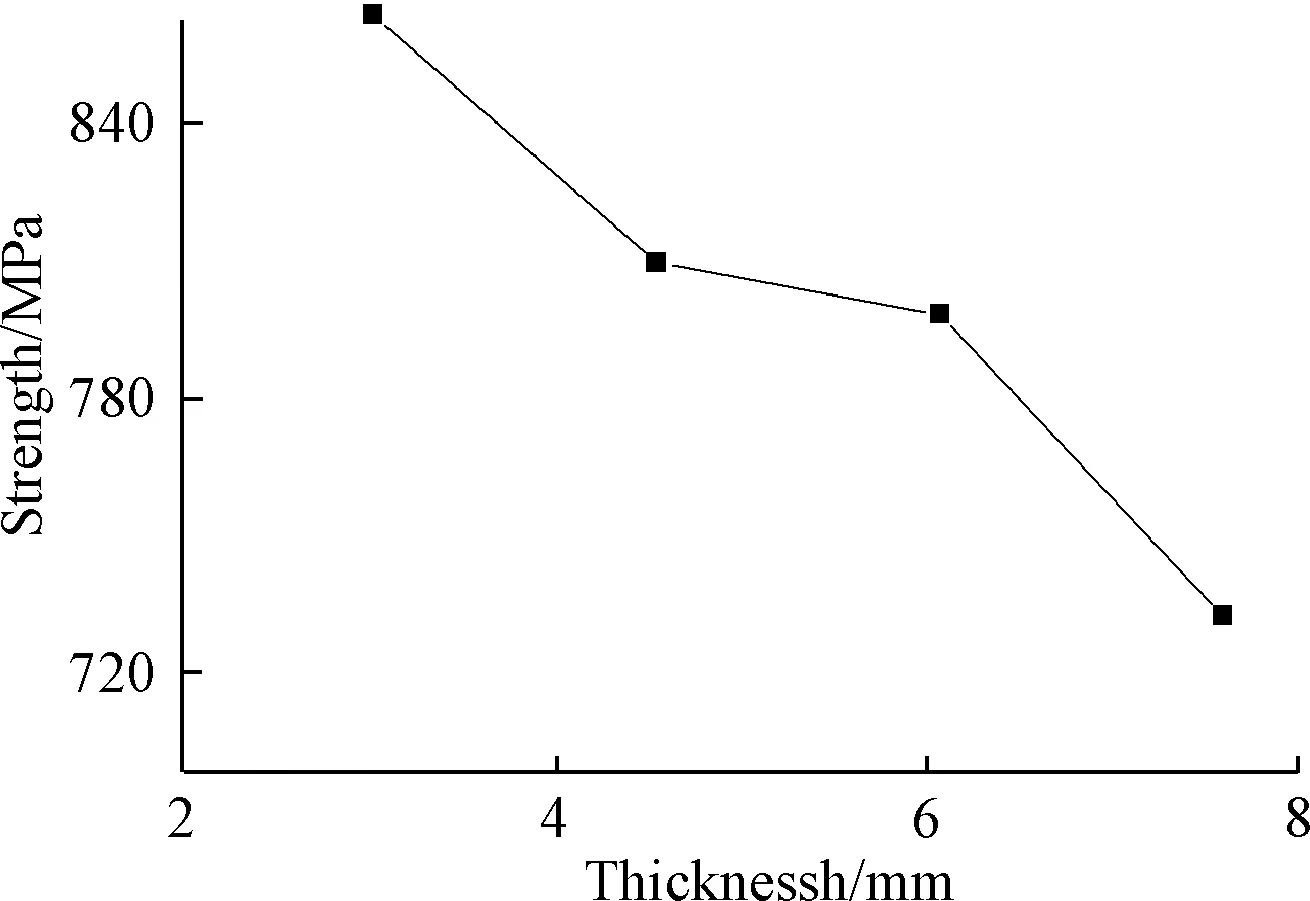
图23 连接强度随厚度变化趋势Fig.23 Curve of connection stiffness with thickness ratio

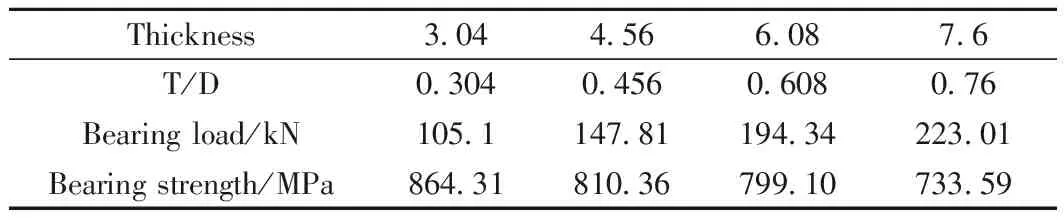
Thickness3.044.566.087.6T/D0.3040.4560.6080.76Bearing load/kN105.1147.81194.34223.01Bearing strength/MPa864.31810.36799.10733.59

表13 多钉连接不同厚度下钉载分配Table 13 Load distribution of muliple-bolt, single-lap thick composite laminate under different thickness

5.3 纵向孔距对连接强度的影响

分别选取纵向孔距为50、60、70和80mm四组孔距进行有限元建模计算来模拟孔距对复合材料连接件连接强度的影响。只通过改变2号钉和3号钉的位置来调整纵向孔距，而材料、1号钉和4号钉的孔距、2号钉和3号钉的孔距、1号钉和4号钉的端距、试验件的长度均与上文的算例相同。不同的孔距所对应的连接强度如表14所示，复合材料-金属双钉单剪连接连接件的连接强度随孔距的变化趋势见图24。当孔距为80mm时连接件连接强度最大比孔距为50mm的连接件的连接强度增加了8.19%，且连接强度随着孔距的增加而增大。可以看出增大孔距可以在一定程度上改善结构的连接强度，但是孔距的增大会造成结构所用的材料的增加和结构质量的增加，尤其是在纵向两排钉以上的情况下。

表14 不同纵向孔距下的连接强度Table 14 Connection stiffness under different vertical hole pitches

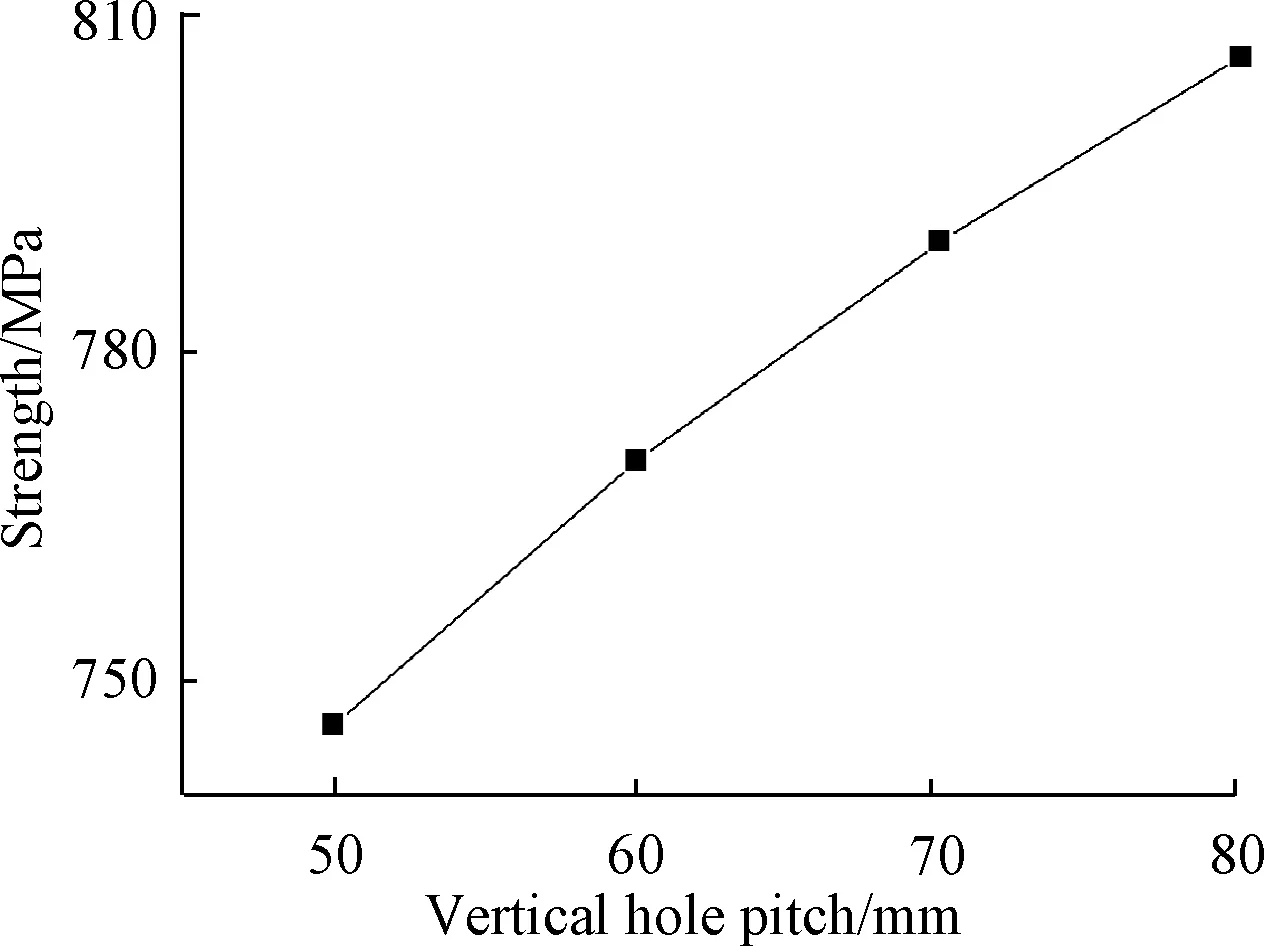
图24 连接强度随纵向孔距的变化Fig.24 Curve of connection stiffness with vertical hole pitches

5.4 横向孔距对连接强度的影响

分别选取横向孔距为50、60、70和80mm四组孔距进行有限元建模计算来模拟孔距对复合材料连接件连接强度的影响。通过对称的改变1、2、3和4号钉的位置来调整纵向孔距，而材料、1号钉和2号钉的孔距、3号钉与4号钉的孔距、1号钉和4号钉端距、试验件的长度均与前文算例相同。不同的孔距所对应的连接强度如表15所示，图25为复合材料-金属双钉单剪连接连接件的连接强度随孔距的变化趋势。在横向孔径达到70mm之前，连接强度随着横向孔径的增加而增加，当横向孔距大于70mm时，连接强度随着横向孔径的增加反而降低。所以在设计结构时，需选取合适的横向孔距来达到最好的承载效果。

表15 不同横向孔距下的连接强度Table 15 Connection stiffness under different horizontal hole pitches

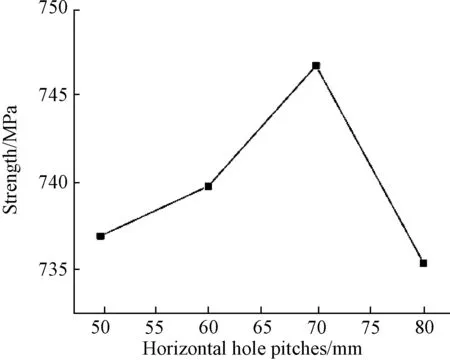
图25 连接强度随横向孔距的变化Fig.25 Curve of connection stiffness with horizontal hole pitches

6 结 论

研究了复合材料厚板-金属双钉单剪螺栓连接的挤压强度试验，并基于Hashin失效准则以及Camanho的刚度退化方法建立了双钉单剪的三维有限元渐进损伤模型。研究了厚度变化和孔距变化等因素对连接件挤压强度的影响，建立了双排四钉有限元模型，研究了孔距对连接件挤压强度的影响。得出以下结论：

1．试验件主要破坏位置出现在复合材料板孔边应力集中位置。

2．将仿真结果与试验结果进行了比对，所建立的三维有限元渐进损伤模型能较好地预测复合材料厚板双钉单剪螺栓连接的挤压强度。

3．数值分析结果表明，随着厚度的增加，连接件的极限逐渐增大，但连接强度却随之降低，两钉的钉载差距逐渐减小，破坏模式保持不变。

4．摩擦力对结构的连接强度有一定的影响。

5．随着宽径比的增加，结构的连接强度也随之增加，但增长趋势逐渐减缓。

6．连接件的连接强度随着纵向孔距的增加而增大，而随着横向孔距增加双排四钉连接件的连接强度变化趋势是先升后降。