电磁波电阻率悬挂孔应力集中分析及优化设计
郭宝左, 刘金柱, 于芳芳, 姚 波, 刘栋梁, 康 凯, 顾继俊
(1.北京环鼎科技有限责任公司,北京102200; 2.中国石油大学〈北京〉,北京102200)
电磁波电阻率悬挂孔应力集中分析及优化设计
郭宝左1, 刘金柱1, 于芳芳1, 姚 波1, 刘栋梁2, 康 凯2, 顾继俊2
(1.北京环鼎科技有限责任公司,北京102200; 2.中国石油大学〈北京〉,北京102200)
电磁波电阻率钻铤悬挂孔产生的应力集中,是钻铤结构强度最薄弱的环节,最终影响钻铤使用寿命。介绍了电磁波电阻率钻铤结构形式,对钻铤两悬挂孔孔间距离以及在圆周方向上与谐振窗的不同夹角分别进行讨论,利用三维建模软件和有限元分析软件模块分别对设计的钻铤结构进行实体建模,在单独施加扭矩载荷和施加压力、扭矩复合载荷2种情况下进行有限元计算,优选出一种合理结构,为下一步的优化设计和加工新型钻铤提供了理论基础。
电磁波电阻率;圆孔应力集中;优化设计;有限元计算;钻铤
0 引言
钻铤在井眼中同时承受内压、外压、轴向载荷、弯曲载荷和扭矩等作用,在复杂载荷作用下,钻铤失效是普遍存在的问题[1]。电磁波电阻率仪器是一种在钻铤上设计构建的仪器,为了实现仪器的地质测量功能,需在钻铤本体上加工孔槽,安装探头和电路等装置,从而导致钻铤强度有所下降。
影响钻铤强度的因素有很多,其中对于钻杆螺纹处应力集中问题已有大量的研究并提出了应力释放槽的解决方法[2-8],而对于随钻仪器表面孔槽位置分布带来的应力集中问题目前还未受到业界重视,相关研究的文章较少。对于随钻仪器,这些孔槽结构是应力集中严重的地方,无疑会成为发生疲劳失效的薄弱点,将严重影响随钻仪器的寿命,甚至影响到钻井的安全。随着随钻仪器的大量应用,如何减少孔槽位置的应力集中,延长随钻仪器寿命,保障钻井安全,这是钻井作业中必须要解决的关键技术问题[2]。
为了最大限度保证电磁波电阻率钻铤的使用寿命,本文对电磁波电阻率钻铤悬挂孔位置进行优化设计,并综合考虑过线孔加工和强度两方面因素,提出了合理的解决方案。
1 结构设计思路
电磁波电阻率仪器由一个整体式无磁钻铤(即天线壳体)和电子线路探管组成,电子线路探管位于无磁钻铤内部,并通过钻铤上的悬挂孔固定在无磁钻铤上,探管内的导线从悬挂中的引线孔引出,其结构如图1所示。
在钻铤的圆周上沿长度方向布置有6个天线环, 每个天线环上有一个长方形走线槽,在两个天线之间有一个谐振窗,谐振窗有孔分别与两边长方形走线槽相通,走线槽内的导线将天线与谐振电路连接起来,并用高压插针进行高压密封,其结构如图2所示。

图1 电子线路探管与钻铤连接示意图

图2 6个天线长方形线槽和3个谐振窗的布置图
2 悬挂孔位置布置方案
如何布置悬挂孔的位置,使得它对钻铤强度影响最小,又便于将悬挂孔内的线引入到谐振窗中,是本文主要讨论的问题。从加工角度考虑,希望悬挂孔与谐振窗越近越好,但从有利于钻挺的强度考虑,则希望悬挂孔远离谐振窗。因此,我们考虑了几种悬挂孔位置方案,分别进行讨论。
2.1 方案一
考虑将悬挂孔设计在沿轴向远离谐振窗的位置,由图2可见,在2个谐振窗所在的圆柱之间,有2个天线环,在2个天线环间有一段光滑的圆柱,考虑将悬挂孔布置在该光滑圆柱上,另外为了避免悬挂孔、长方形走线槽及谐振窗在同一直线上,将悬挂孔与长方形走线槽在圆周方向错开90°,如图3所示。此方案的优点是谐振窗与悬挂孔沿钻铤长度方向分布,且相距较远,钻铤各横截面的有效面积较大,有利于提高钻铤强度;缺点是谐振窗与悬挂孔间有天线环相隔,从谐振窗与悬挂孔间的引线孔必须穿过天线环,而且钻铤长度方向较长,沿轴向打孔不易实现,也不能采用将钻铤断开后再焊接的方法,所以此方案不作考虑。
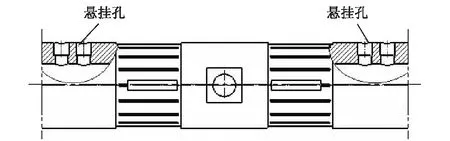
图3 悬挂孔布置在与谐振窗相隔一段天线环的圆柱面上
2.2 方案二
考虑将悬挂孔设计在谐振窗所在的圆柱上,但在圆周方向错开一定角度,如图4所示。由于同一截面上孔的数量增加了,钻铤强度受到影响。所以要对悬挂孔的具体位置进行优化设计。
首先考虑悬挂孔位于圆周方向不同角度时对强度的影响。即从断面看悬挂孔分别与谐振窗口在圆周上夹角分别为60°、90°、120°、150°、180°时的钻铤强度情况,见图4。

图4 悬挂孔位于圆周方向不同角度的情况
其次考虑两悬挂孔不同间距对强度的影响。设两悬挂孔间距分别为45、66、87 mm时,悬挂孔位于与谐振窗口的圆周夹角为60°、90°、120°、150°、180°时的钻铤强度情况。如图5所示。

图5 两悬挂孔间距分别为45、66、87 mm时的情况(圆周方向90°)
为了比较方案二中各种孔距与夹度组合时钻铤的强度,我们分别进行了有限元分析。
3 结构有限元分析
3.1 有限元模型
钻铤在井下所受载荷非常复杂,拉、压、弯、扭、振动都存在,但这些复杂载荷作用在相对较小的孔槽上时,所产生的应力只有拉压应力和剪切应力两种[2],但钻铤处于最下端,所受的拉力较小,所以本文选择施加单独扭矩载荷和压、扭复合载荷作为有限元模型载荷。
电磁波电阻率钻铤外径6.75 in(1 in=25.4 mm),由于天线沿长度方向为3组重复结构,所以只取其中一段进行分析,其基本参数设定为,长l=768 mm,无磁钻铤材料弹性模量E=216 GPa,泊松比u=0.3,建立如图6所示计算模型。

图6 钻铤计算模型
钻铤计算模型的基本机械性能见表1所示。

表1 无磁钻铤基本机械性能[9]
基本假设:不考虑钻铤弯曲变形的影响;不考虑孔壁和钻井液对钻铤的摩擦阻力;钻柱轴线与井眼轴线一致;略去钻铤重力;不考虑接头影响;钻铤微元体所受重力、正压力、扭力均匀分布[10]。
3.2 计算及分析
3.2.1 单独施加扭矩载荷时
先采用SolidWorks建模,再导入ANASYS WORKBENCH 14.0进行模拟计算。取钻挺接头最大扭矩68.8 kN·m[11]为钻铤所受最大扭矩载荷,对各种孔距和与谐振窗的夹角组合分别进行模拟计算。由于计算量较大,下面仅介绍其中2例。
(1)孔距为45 mm、圆周方向夹角60°时的应力情况。
计算模型和网格划分如图7所示。使钻铤模型一端固定,另一端加66800 N·m扭矩载荷,固定和约束扭转如图8所示。

图7 孔距45 mm、圆周方向夹角60°时的模型

图8 固定约束与扭矩
计算结果如图9~11所示,模拟计算后总变形量最大值为0.918 mm,等效应力最大值为3.506×108Pa,最大主应力值为3.522×108Pa。

图9 孔距45 mm、夹角60°单加扭矩时的总变形

图10 孔距45 mm、夹角60°单加扭矩时的等效应力
(2)孔距为87 mm、圆周方向夹角180°时的应力情况。
计算模型如图12所示。扭矩载荷和固定约束同上,具体如图13所示。
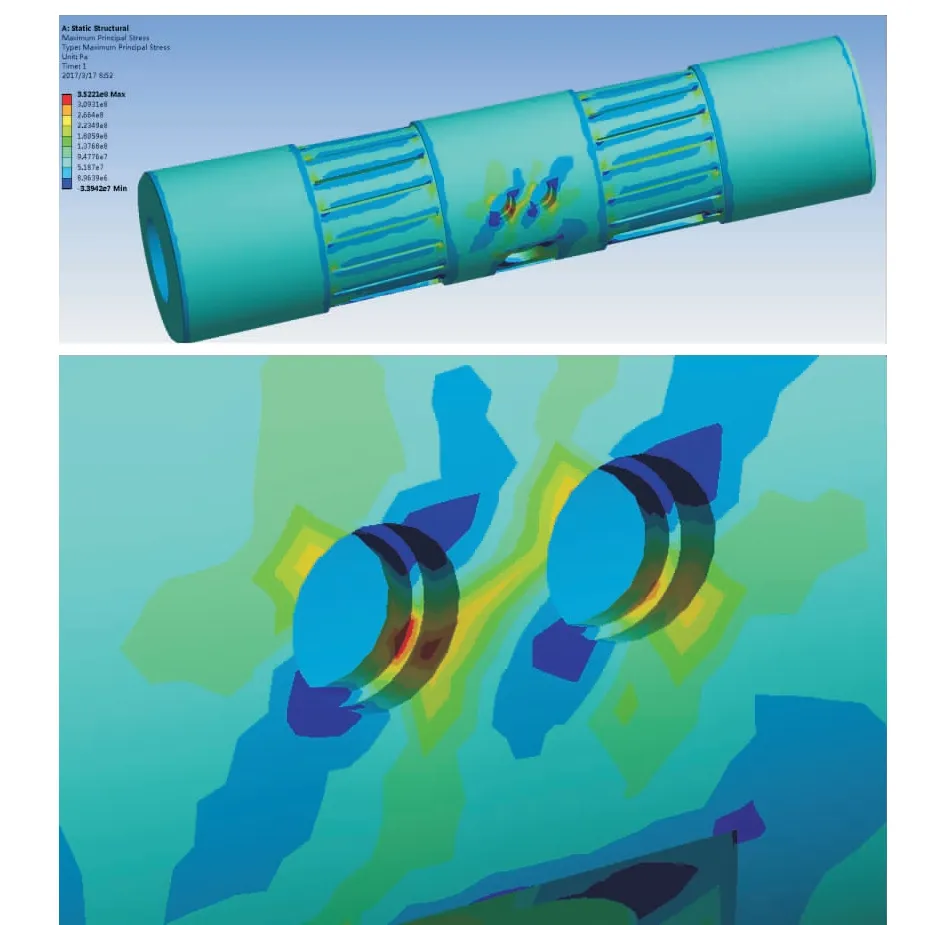
图11 孔距45 mm、夹角60°单加扭矩时的最大主应力

图12 孔距87 mm、圆周方向夹角180°的模型

图13 固定约束与扭矩
计算结果如图14~16所示。模拟计算后总变形量最大值为0.850 mm,等效应力最大值为2.544×108Pa,最大主应力值为2.517×108Pa。

图14 孔距87 mm、夹角180°单加扭矩的总变形
单加扭矩时的全部模拟计算结果见表2。

图16 孔距87 mm、夹角180°单加扭矩时的最大主应力表2 单加扭矩68.8 kN·m时的模拟计算结果

分组与谐振窗夹角/(°)两孔中心距/mm总变形量/mm等效应力/MPa最大主应力/MPa160450.918350.6352.2660.913306.1310.8870.910302.1282.9290450.910317.7335.6660.907313.3295.6870.906275.8277.83120450.902311.5335.2660.900288.0304.3870.900258.6290.04180450.884325.7305.8660.850288.3282.1870.850254.4251.7
将表2的数据用曲线表达如图17~19所示。

图17 单加扭矩时3种孔距的最大等效应力随夹角变化的曲线
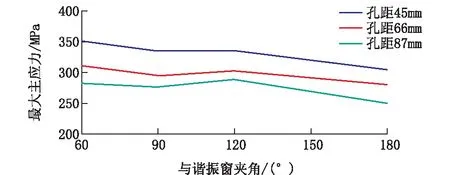
图18 单加扭矩时3种孔距的最大主应力随夹角变化的曲线
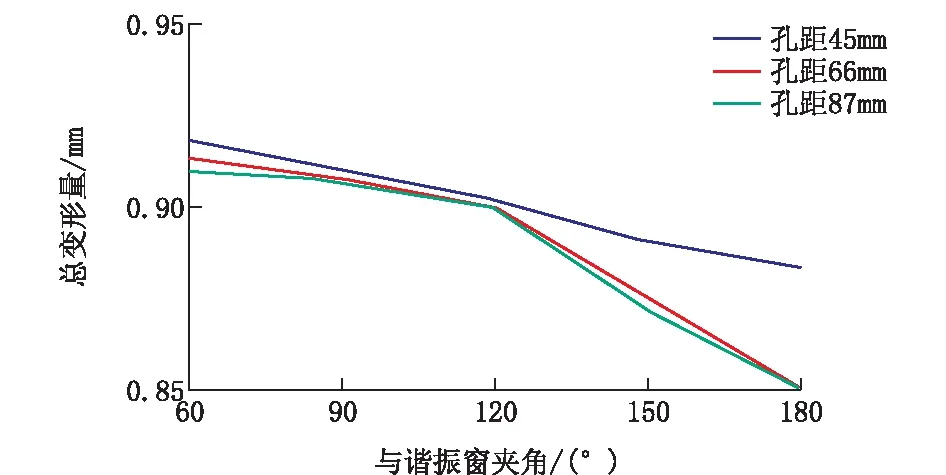
图19 单加扭矩时3种孔距的总变形随夹角变化的曲线
从图17~19可以看出等效应力、最大主应力和总变形量都随着孔距的增加而减小(曲线逐条下移),可见孔距太近,会使应力增加,分析其原因,是孔距太近产生了应力累加效应[2],从图10、11可见,两孔间黄色部分已经相连在一起。
从图中还可以看出同一孔距的等效应力、最大主应力和总变形量都随着夹角的增加而减小,但当夹角>90°后,等效应力曲线变化趋于平缓。分析其原因,当夹角较小时,谐振窗与悬挂孔间也发生了应力叠加现象,当夹角增大到一定程度,应力叠加的影响很小,所以变化趋于平缓。
当孔距和夹角最大时,总变形下降明显,有利于降低疲劳损害。
3.2.2 施加压力和扭矩复合载荷时
同时加载最大钻压和最大扭矩载荷时,设最大钻压为2.5×106N[12],扭矩仍为68.8 kN·m,采用相同的力学模型,对每种孔间距和夹角组合再分别进行模拟计算。下面仍仅介绍其中2例。
(1)孔距66 mm、夹角60°时,施加压、扭复合载荷的模型和计算结果见图20~24。

图20 孔距66 mm、夹角60°时的模型

图21 固定约束与加载压力和扭矩复合载荷

图22 孔距66 mm、夹角60°加压扭复合载荷时的最大总变形

图23 孔距66 mm、夹角60°加压扭复合载荷时的等效应力

图24 孔距66 mm、夹角60°加压扭复合载荷时的最大主应力
由计算结果可知,当两悬挂孔间距66 mm,且位于与谐振窗圆周方向夹角60°时,钻铤模型同时加载2.5×106N压力和68.8 kN·m扭矩载荷,模拟计算后总变形量最大值为1.214 mm,等效应力最大值为6.102×108Pa,最大主应力值为3.309×108Pa。
(2)孔距87 mm、夹角180°时,施加压、扭复合载荷的模型和计算结果见图25~29。

图25 孔距87 mm、圆周方向夹角180°的模型

图26 固定约束与加载压力和扭矩复合载荷

图27 孔距87 mm、夹角180°时加压扭复合载荷的最大总变形

图28 孔距87 mm、夹角180°加压扭复合载的等效应力

图29 孔距87 mm、夹角180°时加压扭复合载荷的最大主应力
由计算结果可知,当两悬挂孔间距87 mm,且与谐振窗夹角180°时,钻铤模型同时加载2.5×106N压力和68.8 kN·m扭矩载荷,模拟计算后总变形量最大值为1.022 mm,等效应力最大值为5.267×108Pa,最大主应力值为2.673×108Pa。
同时加载2.5×106N压力和68.8 kN·m扭矩载荷时的全部模拟计算结果见表3。
将表3的数据用曲线表达如图30~32所示。

表3 加扭矩68.8 kN·m、压力2.5×106 N复合载荷

图30 加压扭复合载荷时3种孔距的 最大等效应力随夹角变化的曲线

图31 加压扭复合载荷时3种孔距的最大主应力随夹角变化的曲线

图32 加压扭复合载荷时3种孔距的总变形量随夹角变化的曲线
从图30~32可以看出压扭复合载荷时等效应力、最大主应力和总变形量的绝对值都比单加扭矩时增加了,而且随着孔距的增加而减小(曲线逐条下移),但孔距66 mm和孔距87 mm的等效应力、最大主应力和总变形值比较接近,而且还有重叠现象,说明当孔距增加到一定值时,压力载荷产生的应力对孔距变化不再敏感。
从图中还可以看出同一孔距的等效应力、最大主应力和总变形量都随着夹角的增加而减小,但当夹角为180°时数值最小。
当孔距和夹角最大时,总变形量下降明显,对降低疲劳损害作用明显。
4 结论
通过比较表2、表3,得出如下结论:
单独扭矩最差:孔距45 mm,夹角60°,等效应力350.6 MPa,最大主应力352.2 MPa;
单独扭矩最好:孔距87 mm,夹角180°,等效应力254.4 MPa,最大主应力251.7 MPa;
复合载荷最差:孔距45 mm,夹角60°,等效应力660.8 MPa,最大主应力413.3 MPa;
复合载荷最好:孔距87 mm,夹角180°,等效应力526.7 MPa,最大主应力267.3 MPa;
无磁钻铤材料的屈服极限758 MPa,上述值都小于屈服极限,但从安全系数和疲劳强度考虑,最终决定采用孔距87 mm,夹角180°的方案。
180°过线孔的具体加工方法如33图所示,分别从谐振窗和悬挂孔向钻铤壁厚上的同一点打出空间交叉的两孔,将两边的过线孔连通。
本文通过有限元模拟,对电磁波电阻率悬挂孔位置进行优化设计,经计算发现不同孔距及在圆周方向不同位置对强度影响的规律:孔距越大、夹角越大应力集中越小,强度越好;夹角越大,总变形量越小,180°时达最小,抗疲劳效果最好。据此选出最佳

图33 180°位置时空间交叉的过线孔加工图
强度设计方案:悬挂孔间距87 mm、与谐振窗夹角180°,使悬挂孔位置对强度影响降到最低,最后提供了过线孔加工方案,这为实际问题的解决提供了重要参考。
[1] 朱荣东,陈平,夏宏泉,等.钻铤螺纹的有限元分析及应力分散槽优化设计[J].西南石油学院学报,2008,30(2):138-141.
[2] 冯永仁,鲍忠利,于会媛.钻铤孔槽结构有限元分析及优化[J].中国海上油气,2013,25(4):38-41
[3] 李鹤林.油井管发展动向及若干热点问题(上)[J].钢管,2005,34(6):1-6.
[4] 陈勇,练章华,林元华,等.钻铤母扣接头改进设计的有限元分析[J].西南石油学院学报,2006,28(6):91-93.
[5] 陶世军,刘剑辉,马建强,等.钻铤螺纹有限元分析及优化改进[J].石油机械,2009,37(10):52-56.
[6] 王炯,王德虎,马福保,等.钻铤断裂失效分析[J].物理测试,2003,(6):34-37,39.
[7] 孙国正.优化设计及应用[M].北京:人民交通出版社,2000.
[8] 管一非.关于应力集中力学概念的进一步探讨[J].长钢纵横,2008,(3).
[9] ISO 10424-1:2004,石油和天然气行业钻井设备:旋转钻井钻柱构件规范[S].
[10] 邬华明,王生楠.基于ANSYS的钻杆的有限元静力分析[J].航空计算技术,2010,40(3):61-64.
[11] 杜晓瑞,李华泰.钻井工具手册[M].北京:中国石化出版社,2014.
[12] 李子丰.油气井钻柱力学及应用[M].北京:石油工业出版社,2009.
Analysis on Stress Concentration Produced by Hanging Holes for Electromagnetic Wave Resistivity Instrument and the Structure Optimization Design
GUOBao-zuo1,LIUJin-zhu1,YUFang-fang1,YAOBo1,LIUDong-liang2,KANGKai2,GUJi-jun2
(1.Beijing Huanding Energy Services, Beijing 102200, China; 2.China University of Petroleum, Beijing 102200, China)
The stress concentration caused by the drill collar hanging holes for the electromagnetic wave resistivity tool is the weakest strength point of the drill collar, which finally influences the service life of drill collar. The structure of the drill collar with electromagnetic wave resistivity instrument is described in this paper, and the schemes of distance between the hanging holes of drill collar and the different angles with the resonant window in the circumferential directions are discussed. The entity models of drill dollar structures are made by three-dimensional modeling software and finite element analysis software module, the finite element calculations are performed under 2 conditions of imposing single torque load and imposing the compound load of pressure and torque to select a kind of reasonable structure, which can be a theoretical basis for optimal design and manufacture of new drill collar next.
electromagnetic wave resistivity; round hole stress concentration; optimal design; finite element calculation; drill collar
2017-04-26
郭宝左,男,汉族,1966年生,从事测井仪器设计制造工作,北京市昌平区创新路12号,gbz2012@163.com。
P634.4;TE921+.2
A
1672-7428(2017)07-0041-07
——以淮南矿区为例

