分数槽集中绕组双转子感应电机电磁耦合特性的分析

许祥威，骆 皓,，侍正坤,3，赵家欣，倪喜军

(1.南京工程学院 电力工程学院，南京 210013;2.天津瑞能电气有限公司，天津 300381;3.南京南瑞继保电气有限公司，南京 211100)

0 引 言

双馈风力感应发电机工艺简单、可靠且配套变流器容量小，但功率因数随极对数增加而显著降低，无法实现直驱而需采用高速齿轮箱[1-3]，增加了传动链的复杂程度，严重影响了系统性能[4-5]。因此，双馈风电机组若能突破低速大转矩直接驱动的技术瓶颈，将在传动链效率、转矩密度、成本和可靠性等方面充分发挥优势。

在此背景下，诸多学者近年来深入研究了分数槽集中绕组，旨在以少槽实现多对极，并将其应用于大型低速永磁同步发电机[6]。目前针对分数槽集中绕组电机的研究主要可归纳为4个方面：谐波极对数、基波/谐波绕组系数、电感参数和永磁同步电机的齿槽转矩。文献[7-10]给出了符合分数槽集中绕组条件的槽极配合选择表，并对分数槽集中绕组单元电机的单个线圈、线圈组、相绕组和三相绕组的磁动势进行了分析，指出分数槽集中绕组丰富的谐波磁动势会对电机造成不良影响。文献[11-15]通过引入匝数函数和绕组函数，分别描述不同电机绕组在空间的实际分布情况和绕组所产生的磁动势波形，量化分析分数槽集中绕组永磁同步电机的自感和互感。通过以上分析可知，此类电机电感参数与传统的采用短距分布绕组的同步电机电感参数有许多差异，比如FSC(分数槽集中)绕组高自感、低互感的特性，虽然高自感、低互感有利于提升电机容错性能，但降低了永磁电机的功率因数和转矩密度。因此，感应发电机直接采用此类绕组方案，将导致更低的功率因数和转矩密度，难以实现直驱。

为此，提出一种以轴向磁场电机结构为基础，采用极槽比接近1的FSC绕组，针对定子磁动势极对数频谱中的一对主导分量(基波极对数磁动势和幅值最大的谐波极对数磁动势)进行双转子交流励磁的直驱双馈电机，并简述其基本结构、工作原理及电磁耦合特性，引入绕组函数计算电感参数，分析高次谐波对它的影响，并与有限元分析结果对比，验证了理论分析的准确性。

1 分数槽集中绕组双转子感应电机的基本结构及工作原理

1.1 基本结构

提出的一种分数槽集中绕组双转子双馈电机，是由二个转子和一个定子构成的双气隙轴向磁场电机，采用极槽比接近1的FSC绕组，针对定子磁动势极对数频谱中的一对主导分量(基波极对数磁动势和幅值最大的谐波极对数磁动势)进行双转子交流励磁。图1为此双馈电机剖面图。此方案充分利用了FSC绕组产生的磁场少槽多极的特点，显著降低了双转子的额定同步转速；其次，充分利用了上述定子极对数频谱中的一对主导分量进行电磁功率传递，显著增大了电机互感，提高了电机功率因数并提升了转矩密度；再则，减小铁心内圆直径并充分利用轴向空间进行线圈绕制，显著减小了槽面积并增加了轴向导磁面积，有效减小了电机直径并进一步提高了电机的功率因数和转矩密度。如图2所示双馈电机三维结构图，该单元电机定子由独立的“工”字形硅钢片单元铁心、集中式独立绕组、非导磁铁心紧固环组成，无轭定子铁心设计，较好地实现了定子和两个转子之间的磁场耦合。两个转子均单侧开槽，分别嵌套集中式独立绕组。

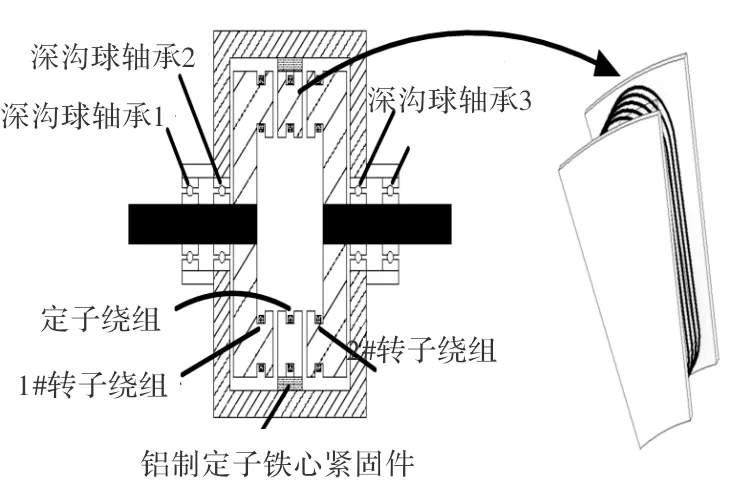
图1 双馈电机剖面图

图2 双馈电机三维结构图

1.2 工作原理

如图3所示，定子三相绕组与电网相连，1#转子与2#转子三相绕组分别通过变流器实现交流励磁。定、转子电流激励产生的磁通，均经过1#转子轭、1#转子绕组、1#转子侧气隙、定子绕组、2#转子侧气隙、2#转子绕组、2#转子轭形成回路。定子绕组单元电机的主导磁场极对数p1和p2，1#转子和2#转子的主导磁场极对数分别为p1和p3、p2和p4。1#转子与定子绕组之间的互感主要通过p1对极磁通匝链，2#转子与定子绕组之间的互感主要通过p2对极磁通匝链。通过双转子协调交流激励，实现定子电流的有功无功解耦控制。

图3 双馈电机工作原理图

图4 双馈电机磁路模型

当气隙1和气隙2磁阻分别为Rag1和Rag2时，双转子电机在不同绕组(定子绕组、1#转子绕组和2#转子绕组)励磁时的磁路如图4所示。通过简单的等效变换，图中的三个磁路图均可等效为磁动势Fm和一个磁路总磁阻Rm，其中

Rm=2(Rag1+Rag2)

(1)

因此，在该磁动势下产生的磁通

(2)

气隙1和气隙2的宽度和横截面积理论上相等，并且文中分析工作不考虑齿槽效应对磁场的影响，故气隙磁密：

(3)

式中，μ0为真空磁导率，Sag为气隙的横截面积，lag为气隙长度。

从上述分析可以看出，对于不考虑齿槽效应、均匀分布、忽略铁心磁阻的电机而言，其气隙磁密分布与气隙磁动势分布呈正比关系，比例系数为真空磁导率和气隙长度的比值。

2 分数槽集中绕组双转子感应电机的基础理论

2.1 分数槽集中绕组磁动势频谱分布

单元电机(双层绕组的单元电机)相数为m,定子槽数为Q,极对数为p。针对于单个线圈分数槽集中绕组的节距y=1，即1个线圈绕制在1个齿上，设该线圈匝数为Nc，当线圈中通入角频率ω电流振幅Im的i=Imcosωt交流电流时，线圈产生的脉振磁动势为Fc=Nci。当电机磁路为线性，即磁路不饱和并忽略齿槽效应，且不考虑铁心部分磁路上的磁动势降，可以把单个线圈产生的矩形磁动势分解为一系列谐波磁动势[16]。单相分数槽集中绕组产生的磁动势是该绕组下空间上处于不同位置的单个分数槽集中绕组线圈磁动势的矢量叠加。这样就可以写出单相分数槽集中绕组线圈产生的磁动势在空间中的分布。不同位置的线圈产生的磁动势体现在函数表达式上，即产生一个机械偏转角度θ0，对于线圈中心线处于θ0的线圈产生的磁动势，其表达式：

(4)

(5)

(6)

式中，kyv和kqv分别为绕组的短距系数和分布系数。根据式(4)可以看出，为使主导极绕组系数较大，定转子耦合程度更好，列出两种特殊形式槽/极的分数槽集中绕组。

(1)Q=2p±1

此类绕组的A相线圈依次为1,-2,3,-4…Q/3,其中负号代表线圈反绕。

(7)

(2)Q=4mk=2p±2(k=1,2...)

此类绕组的A相线圈依次为1,-2,3,-4…-(Q/2+1)…(2Q/3)

(8)

其中,α0=2π/Q。

此时绕组系数kwv为

kwv=kyv*kqv

(9)

并根据式(7)到式(9)，通过计算可以发现其绕组系数在一个区间内存在一对相等的值，并且呈现一定的周期性和对称性。即：

(10)

由一相绕组磁动势分布可知三相合成磁动势分布为

(11)

式(11)反映的是绕组激励下各次谐波极对数产生的三相合成磁动势是沿着θ正或负方向移动的旋转磁动势，机械角速度为±ω/v。不同的槽极绕组磁动势主导极极对数各不相同，不同的三相谐波合成磁动势其旋转方向也不同。所以选择不同的槽极配合会影响电机的电磁耦合特性，进而影响电机性能。

2.2 电磁耦合特性

用绕组函数量化电机的磁链、感应电压及电感等参数是分析电磁耦合特性的一般方法。利用匝数函数、绕组函数来描述绕组在空间中的实际分布情况及磁动势分布情况，进而分析定转子产生的各次谐波极对数磁场之间的强耦合及弱耦合情况，为双转子感应电机的槽/极选取提供理论基础。定子激励下，转子A相的感应磁链为

(12)

文中以空间谐波磁场极对数和转差率为自变量，构造二维的定转子磁感应工作区间，并在该区间内分别研究定转子感应磁链的幅值、感应电动势的幅值，分析各次谐波耦合程度。对应于不同转差率下各次谐波Bs的频率不同，所以其相对转子的运动方向及速度也各不相同，为此分析不同谐波下Bs在不同转差率下的函数：

(1)v=3k

(13)

(2)v=1/3k-1

(14)

(3)v=3k+1

(15)

由式(13)到式(15)，可知在相同转差率下，转子A相的各次谐波极对数的磁链幅值与定子激励下所产生的磁场的一对主导极谐波磁场，以及转子绕组匝数在空间的分布相关，而转子绕组匝数在空间的分布又与槽极配合相关，不同的槽极配合使得其主导极对数不同，从而转子上产生磁链幅值的大小也受到影响。不同转差率下，其各次谐波产生的感应磁链的频率各不相同，使得其感应电压的幅值各不相同，从而影响电磁功率传递。

2.3 电感参数

文中所提出的分数槽集中绕组双转子感应电机较传统感应电机，其电感参数不仅比传统电机更为庞大，建立它的电感矩阵对其进行坐标变换进而简化模型是解决此类新型电机的关键之处；而且由于分数槽绕组中含有一对主导极对数磁动势及派生磁场，使得电感参数存在谐波漏感，通过绕组函数总结出电感参数的一般表达式，是分析此类电机有效的方法。此类电机电感分为两种，第一种是自感和定子或转子不同绕组之间的互感，不随绕组空间位置改变而改变。第二种为定子或转子1任一相绕组和转子2任一相绕组之间的互感，这类互感随着绕组空间位置的改变而改变。为此可以根据磁链与电流的关系，计算出相对应的电感。

九个绕组的磁链表示为

(16)

其中式(16)中L是双转子感应电机电感矩阵，矩阵中的参数为各个相绕组中的电感参数。例如Lss代表定子中各相自感。

对于第一类互感和自感，其匝数函数不变，也就是绕组在空间位置上是不变的。对于第二类互感，由于分数槽集中绕组电机气隙径向磁密含有大量高次谐波分量，不能像传统电机那样仅在基波下分析第二类互感的变化值，还应考虑不同频率下谐波的影响。并且转子是随时间变化的，定子激励下产生的单相绕组的磁动势波可以分解为一个正向推移的圆形旋转磁动势波与一个反向推移的圆形旋转磁动势波，使得转子旋转时无相对运动，故转子旋转的角度即匝数函数变化的角度，即：

(17)

(18)

3 电磁场的有限元分析计算

3.1 槽极配合选取

依据电磁耦合特性，比较三种模型下在转差率s=0时，定子绕组半径r为40mm,定转子匝数N=100,气隙长度为1mm，铁心长度为1m，交流电流幅值为1A。定子激励，转子开路时，两个转子的感应磁链幅值。三个模型依次是：模型Ⅰ为定子14极18槽，1#和2#转子依次为14极15槽，22极24槽;模型Ⅱ为定子14极18槽，1#和2#转子依次为14极15槽，10极12槽;模型Ⅲ为定子14极18槽，1#和2#转子依次为8极9槽，26极27槽。选取的定子绕组主导极对数都是7和11对极。比较定子绕组激励下其主导极谐波磁场在转子A相产生的感应磁链幅值。

表1 各个模型下的最大感应磁链幅值

由表1所示，在相同条件下，模型Ⅰ中1#转子A相最大磁链幅值为0.476Wb，对应的谐波极对数为7对极，2#转子A相最大磁链幅值为0.308 Wb，对应的谐波极对数为11对极；模型Ⅱ中，1#转子A相最大磁链幅值为0.476 Wb，对应的谐波极对数为7对极，2#转子A相最大磁链幅值为0.394 Wb，对应的谐波极对数为7对极，11对极为0.01 Wb，远小于主导极对数相同时，11对极谐波磁场产生的磁链幅值，呈现弱耦合；模型Ⅲ，1#转子A相最大磁链幅值为0.0864 Wb，对应的谐波极对数为5对极，7对极谐波磁场产生的感应磁链幅值为0.0418 Wb，2#转子A相最大磁链幅值为0.069 Wb，对应的谐波极对数为11对极。由以上三个模型，可以知道。主导极是否相同决定着定子绕组激励下产生的一对主导极对数在转子侧产生的感应磁链幅大小。故文中采取模型Ⅰ。

3.2 仿真模型

在进行Ansys软件仿真时，如果采用轴向磁场三维电机进行建模，软件运行速度慢，效率低。为应对较大的仿真模型计算量，沿不同半径将电机展开为若干直线电机模型，并使用一系列二维有限元的结果加权平均，实现电机的二维有限元等效模型参数如图5所示直线电机仿真图，其中大写字母表示线圈为正绕，小写字母表示反绕[17]。

图5 直线电机有限元仿真模型

表2 分数槽集中绕组感应电机参数

3.2 电感参数

对于2D模型下的有限元分析法计算出的自感与第一类互感参数，比较主导极谐波，前100次谐波，前500次谐波对第一类电感参数的影响。如表3所示不同谐波下的自感与互感对比可以发现，分数槽集中绕组由于存在主导极次谐波并且主导极对数谐波幅值占的比重大，所以计算电感参数时不能像整数槽绕组一样只计算基波，忽略谐波电感，需要考虑主导极对数谐波。并且对比100次和500次谐波下的电感可以发现，高次谐波对于第一类电感参数影响已经变得很小。由于忽略了端部漏感及槽漏感使得结果与实际值仍然存在误差。

表3 不同谐波下的第一类电感对比

图6为有限元仿真结果，设置1#转子转速为3000/7 r/min，2#转子转速为-3000/11 r/min，可以从图中看出第二类互感的变换周期依次为0.14 s，0.22 s,0.08 s。

图6 定转子A相之间相互的互感

利用解析法求得定子激励下产生的7对极，前100次，前500次和前1000次谐波下在1#转子绕组A相产生电感，并列出解析值和有限元的峰值所获取的电感参数。

图7 定子与1#转子A相互感

表4 高次谐波下第二类互感对比

由图7可知，7对极谐波产生的电感与有限元仿真结果曲线几乎重合，说明7对极在互感参数中起主导作用，前100次谐波相比有限元值其峰值很大，说明前100次谐波对电感参数影响比较大。前500次和1000次谐波曲线也逐渐接近于有限元结果，并且前500次和前1000次谐波图像几乎重合，说明500次谐波之后对于电感参数影响较小。由表4所示的峰值比较，也印证了500次谐波对于电感参数影响较小。

4 结 论

文中提出了一种分数槽集中绕组的双转子感应电机：对比分析了三种模型下的电磁耦合特性并通过引入绕组函数解析双转子电机的自感和互感参数，解析了高次谐波对电感参数的影响，与有限元所分析的参数值进行对比，获得如下结论：

(1)通过对主导极对数的频谱分布、各次谐波磁动势幅值、定转子间谐波极对数磁场的耦合特性的研究发现，定子绕组激励时产生7和11对极谐波磁动势分别与1#转子中产生7对极谐波磁动势、2#转子中11对极谐波磁动势呈现强耦合，而另外的非主导谐波极对数磁动势与定子绕组弱耦合。

(2)利用绕组函数归纳了双转子感应电机的互感和自感的计算方法。并发现主导极谐波产生的电感参数占主导地位，前500次谐波对电感参数影响较大，500次谐波以后影响较小。