新型16相磁悬浮开关磁阻电机解耦特性及数学模型
孙传余,李井凯,庄 鹏,曹茂永
(1.山东科技大学 机械电子工程学院,山东 青岛 266590;2.山东科技大学 电气与自动化工程学院,山东 青岛 266590)
0 引 言
磁悬浮开关磁阻电机(Bearingless Switched Reluctance Motor,BSRM)是将磁悬浮技术应用到开关磁阻电机中,使电机兼具开关磁阻电机可靠性高、调速性能好和磁悬浮技术无摩擦、功率损耗低的优点,是第三代人工心脏中常用的动力部件[1-3]。传统BSRM工作时,对转矩与悬浮力的控制存在耦合,严重影响电机性能,增加了控制难度。
根据产生悬浮力绕组的不同,现有BSRM可分为双绕组BSRM和单绕组BSRM。双绕组BSRM将绕组分为转矩绕组和悬浮力绕组,两者电流独立控制,通过调节悬浮力绕组电流的大小来实现悬浮力的调节,但悬浮力绕组通电产生的磁力线与转矩绕组产生的磁力线会出现交链,使得控制难度加大[4-5]。单绕组BSRM的每相绕组电流都由转矩分量和悬浮力分量组成,只能通过复杂的控制策略进行解耦,解耦难度较大[6]。文献[7]将定子齿划分为宽齿与窄齿,以消除悬浮力调节对转矩的影响,但解耦效果不够理想;文献[8]通过增大转子齿的极弧使电感出现平顶区,通过对转矩与悬浮力分区域控制来解除耦合,但是该结构的转矩输出存在死区。
针对传统BSRM的控制耦合问题,提出了一种新型16相BSRM,通过转子结构的改进实现了悬浮力和转矩控制的自然解耦,解决了现有BSRM控制策略复杂、功率损耗高的问题,并求取了该电机转矩与悬浮力的数学模型。
1 电机结构及原理
1.1 新型16相混合转子齿BSRM结构
新型16相BSRM结构如图1所示。电机有16个定子齿,依次命名为A-P;绕组有16相,依次命名为a-p,每相绕组绕在两个相邻定子齿上且在两定子齿上的绕向相反,每个定子齿上绕有两相绕组,各相绕组独立控制。电机采用分块混合转子齿结构,转子可分为悬浮力齿、转矩齿和支撑部件三部分。悬浮力齿为宽齿,共有3个,3者在空间上两两相差120°;转矩齿为U形结构,共有3个,3者在空间上两两相差120°;以铸铝作为转子齿的支撑部件,悬浮力齿与转矩齿嵌在转子支撑部件中。
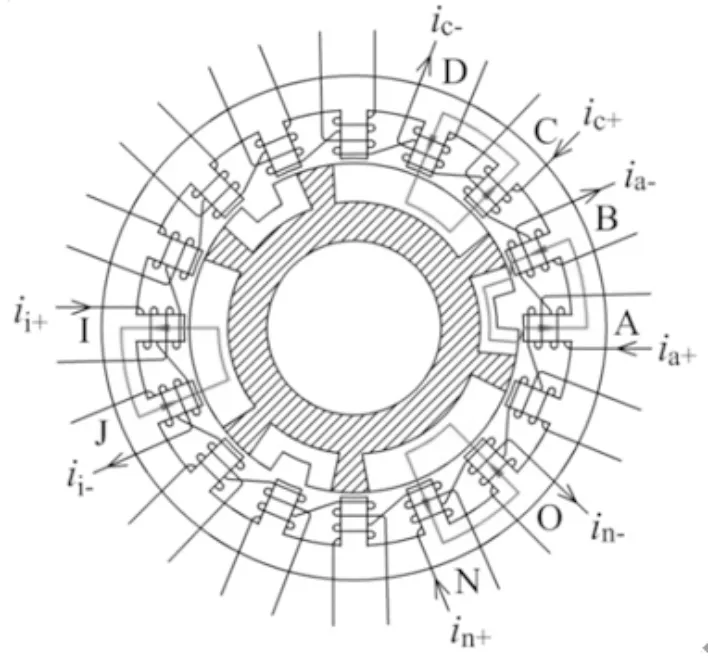
图1 新型16相BSRM结构图
1.2 转矩与悬浮力产生原理
定义θ为转子位置角、转矩齿与定子齿A、B完全对齐时θ为0°,定义逆时针方向为转子旋转正方向,由电机结构可知,转子步距角为7.5°。当转子位于图1所示位置时,绕在定子齿A和定子齿B上的a相绕组为转矩绕组,ia+和ia-分别为a相绕组的电流输入端和电流输出端;d相、i相和n相绕组为悬浮力绕组,id+、ii+、in+分别为d相、i相和n相绕组的电流输入端,id-、ii-、in-分别为d相、i相和n相绕组的电流输出端。理想状态下,a相绕组通电后产生的磁力线全部进入邻近的转矩齿,形成如图1定子齿A、B处所示的闭合回路,产生电磁转矩。当θ∈[-22.5°,0°]时,c相绕组产生的磁力线进入所正对的悬浮力齿,在定子齿C、D与悬浮力齿之间形成闭合回路,由于定子齿C、D与悬浮力齿的正对面积保持不变,定子齿C、D对悬浮力齿只产生大小和方向都不变的悬浮力。i相绕组和n相绕组与c相绕组工作原理相同,通过调节三相悬浮力绕组电流的大小,能够产生任意大小和方向的悬浮力。当θ∈[-7.5°,0°],a相绕组通电时,定子齿A、B在对转矩齿产生电磁转矩的同时,也会产生悬浮力FA和FB,FA和FB的大小与方向随θ而变化,因此转子所受悬浮力为8个力的合力。电机工作时,对三相悬浮力绕组的电流大小进行调节,以平衡掉转矩齿上受到的悬浮力,使转子在径向上稳态悬浮。图2所示为悬浮力产生原理,其中,FA、FB、FC、FD、FI、FJ、FN、FO分别为θ∈[-7.5°,0°]时,定子齿A、B、C、D、I、J、N、O对转子产生的径向悬浮力。

图2 悬浮力产生原理
1.3 解耦原理
首先,通过增大悬浮力齿极弧,消除了悬浮力调节对转矩的影响;其次,令悬浮力绕组产生的磁力线仅作用于悬浮力齿,转矩绕组产生的磁力线仅作用于转矩齿,消除了悬浮力绕组和转矩绕组的磁力线交链,从而解除了转矩与悬浮力的控制耦合。
2 解耦性能验证
新型16相BSRM的参数如表1所示。根据表1所示参数,在有限元仿真软件Ansys Maxwell中建立样机模型。图3为θ=-7.5°,ia、ic、ii、in均为2A时,Ansys Maxwell输出的磁力线分布图,由图3可以看出,各磁力线回路之间相互独立。

表1 新型16相BSRM参数

图3 电机磁力线分布图
从励磁线圈的相对位置可知,θ∈[-7.5°,0°]时,定子齿C上的绕组电流ic对定子齿B上的绕组磁链ΨB影响最大,因此以ic为变量来检测悬浮力绕组电流对转矩绕组磁链的影响。图4为ia=2A时,不同ic下ΨB的值。图4显示,ΨB的大小和斜率不受ic影响,即悬浮力绕组电流对转矩绕组的磁链没有影响、调节悬浮力绕组电流不影响转矩输出。

图4 不同悬浮力绕组电流下的转矩绕组磁链
当θ∈[-22.5°,0°]时,c相绕组始终为悬浮力绕组,因此以c相绕组为例来分析转矩绕组电流对悬浮力绕组磁链的影响。图5所示为ic=2A时,不同大小的转矩绕组电流下定子齿C上悬浮力绕组磁链ΨC的值。图5表明,在θ∈[-22.5°,0°]范围内,转矩绕组电流对ΨC的值基本没有影响,即转矩绕组电流对悬浮力绕组的磁链没有影响。
由图4和图5可得:该电机从结构上基本实现了转矩与悬浮力的解耦控制。

图5 不同转矩绕组电流下的悬浮力绕组磁链
3 数学模型
在求取转矩与悬浮力数学模型时作如下假设:转子无径向偏心和轴向位移;电机不存在磁饱和与漏磁;忽略定子铁心和转子齿的磁阻。
3.1 转矩数学模型及有限元验证
a相绕组与c相绕组的等效磁路模型如图6所示,其中图6(a)为a相绕组等效磁路,图6(b)为c相绕组等效磁路。

图6 a相绕组与c相绕组等效磁路模型
图中,N为绕组匝数,ia为a相绕组电流;PA、PB分别为定子齿A、B处气隙磁导,PA=PB;ΦA、ΦB分别为定子齿A、B处磁通,ΦA=-ΦB;ic为c相绕组电流;PC、PD分别为定子齿C、D处气隙磁导,PC=PD;ΦC、ΦD分别为定子齿C、D处磁通,ΦC=-ΦD。由图6(a)可得a相绕组自感系数:
(1)

(2)

图7 定子齿A处磁路分割模型
a相绕组储能公式为
(3)
WAB对θ求偏导可得转矩数学模型:
(4)
将式(1)和式(2)代入式(4),化简后得:
(5)

图8 有限元仿真输出转矩与数学模型输出转矩
图8为ia分别为2A和2.5A时,有限元仿真与数学模型输出的转矩对比图。由图8可得,该模型可较为精确地描述新型16相BSRM的转矩特性。
3.2 悬浮力数学模型及有限元验证
当θ∈[-7.5°,0°]时,设转子在x轴上的位移为α,在y轴上的位移为β,此时,定子齿A、B处的平均气隙厚度δxA和δxB可分别表示为δ-αcosθ-βsinθ和δ-αcos(π/8+θ)-βsin(π/8+θ)[10]。由假设可知,α、β均为0。
因定子齿A、B产生的悬浮力方向不同,需对两者进行单独计算。a相绕组在定子齿A、B处的储能分别为WA和WB,令FA和FB的合力为Ft,则Ft在x和y方向的径向力分量Ftx和Fty可为
(6)
a相绕组在定子齿A、B处的储能WA和WB对α和β的偏导求得如下:
(7)
当θ∈[-22.5°,0°]时,设定子齿C与悬浮力齿的正对面积为S,由磁导定义可得:PC=PD=μ0S/δ,其中S=πrh/24。由图6(b)列等效磁路方程可得ΦC=-ΦD=icNPC。单个定子齿C、D产生的悬浮力FC、FD和定子齿C、D产生的悬浮力合力FCD可分别表示如下:
(8)
在式(8)的基础上可得FCD在x方向和y方向的分量FCDx和FCDy:
(9)
式中,β1为FCD与x轴正方向夹角,β1=5π/16。
i相绕组和n相绕组的等效磁路与c相绕组相同,同理可得定子齿I、J产生的悬浮力合力FIJ在x方向、y方向的分量FIJx、FIJy和定子齿N、O产生的悬浮力合力FNO在x方向、y方向的分量FNOx、FNOy:
(10)
式中,β2为FIJ与x轴正方向夹角,β2=-15π/16;β3为FNO方向与x轴正方向夹角,β3=-5π/16。
由前述分析可知,转子在x方向所受的合力Fx和在y方向所受合力Fy可为
(11)
结合式(6)、式(7)、式(9)、式(10)与式(11),可得新型16相BSRM的悬浮力数学模型:
(12)
由式(12)可知,通过调节绕组电流ia,ic,ii和in的值,可以产生任意方向和大小的悬浮力。当θ∈[-7.5°,0°]时,ia和θ作为自变量,通过改变ic,ii和in的值对悬浮力进行调节,以使转子保持稳定悬浮。图9为ia,ic,ii和in均为2A时,有限元仿真输出的Fx、Fy与数学模型输出的Fx、Fy的对比。从图9可以看出,式(12)所得Fx能够较为准确地描述转子在x方向上的受力情况;式(12)所得Fy与转子在y方向上的受力变化趋势相同,但是精确度相对较低。

图9 有限元仿真输出悬浮力与数学模型输出悬浮力
4 结 论
文章研究了一种新型16相磁悬浮开关磁阻电机,通过对转子结构进行创新设计,消除了悬浮力调节对转矩的影响和不同绕组间的磁力线交链。利用有限元仿真软件对该电机进行磁链特性分析,证明了悬浮力绕组电流对转矩绕组磁链无影响、转矩绕组电流对悬浮力绕组磁链无影响,即该电机能够有效解除转矩与悬浮力的控制耦合。通过等效磁路法推导了电机转矩和悬浮力数学模型,并利用有限元仿真输出的转矩与悬浮力进行验证,结果表明:所求得的数学模型能够对该电机转矩和悬浮力进行较为准确的描述,为后期转矩和悬浮力的控制及优化奠定了基础。

