基于变分模态分解与形态学分形的压缩机故障诊断方法

李玉倩

（大庆石化公司水气厂污水联合车间，黑龙江大庆 163711）

1 引言

往复压缩机是石油化工、冶金、矿业、电力等行业的核心设备，其任务通常为输送易燃易爆性流体与高压空气，有很高的安全性与可靠性要求，对其开展故障检测与诊断工作有助于保证工业生产平稳运行，提高经济与综合效益[1]。往复压缩机的故障机理复杂，故障模式多样，振动激励源多，振动传递路径复杂，这些因素会导致多源信号间的耦合与冗余现象，给监测信号的分析处理带来了困难。常规的振动信号处理技术，如信号统计特征分析、信号关联与冗余分析、傅立叶变换方法、小波分析以及时间序列模型分析等难以应用在往复压缩机故障诊断工作中[2]。因此本文以往复压缩机的典型故障为研究对象，以保证设备安全、稳定运行为目的，提出了基于变分模态分解方法和形态学分形的特征提取技术，将其引入到往复压缩机故障诊断技术研究中。试验验证结果表明该方法能够提高往复压缩机故障的识别准确率，对往复压缩机运行的安全性与平稳性具有重要的现实意义。

本文第二部分将简述变分模态分解方法，第三部分将简述形态学分形方法，第四部分利用支持向量机（SVM）对利用变分模态分解与形态学分形方法获得的往复压缩机特征进行识别，计算故障识别准确率，最后给出本研究的结论。

2 变分模态分解

Dragomiretskiy和Zosso于2014年提出了变分模态分解（VMD）算法。该算法是一种有严格理论和全新筛分原则的信号分析方法，其主要作用是对不同信号分量的频率进行分离。主要手段是求解约束变分模型，基于频率分割方法，利用多个有限带宽的模态函数（BLIMF）自适应的表达信号频率成分。下面对于给定信号x（t），给出变分模态分解算法的步骤。

2.1 变分模型构建

（1）有限带宽的内禀模态函数表达式如下（Band-Limited Intrinsic Mode Function，BLIMF）

（2）构建解析信号获取单边谱，然后混频

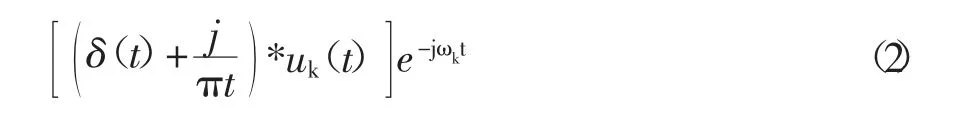
（3）计算各模态函数带宽：利用高斯平滑方法（即L2范数梯度的平方根）解调信号（2）；

（4）结合约束条件，构造优化变分模型，其结果如公式（3）所示

式中，K是BLIMF分量{uk}={u1，u2，L，uk} 的数目，{ωk}=｛ω1，ω2L，ωK｝ 是uk（t）中心频率，δ（t）是狄利克雷函数。

2.2 求解变分模型

下面求取变分模型（3）的最优解，引入二次惩罚因子α以提高在高斯噪声环境下的信号重构准确性，引入拉格朗日乘子λ（t）保证模型的约束刚度。构建增广拉格朗日函数L（｛uk｝，｛ωk｝，λ）如式（4）所示，此时变分模型的构建问题就由一个约束问题转化成了一个无约束问题。

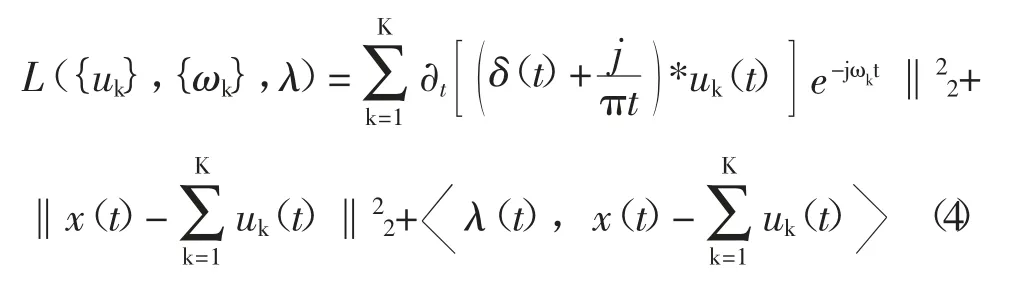
之后求解增广拉格朗日函数的鞍点，更新｛uk｝，｛ωk｝和λ的数值，采用的主要方法为乘数交替法。获得变分模型（3）的最优值，进而将给定信号x（t）分解为K个BLIMF分量。

VMD算法流程图如图1所示。

综上所述，变分模态分解法通过构建多个自适应维纳滤波组，结合狄拉克分布，以拉格朗日因子与二次惩罚等数学理论为基础，以非递归形式将信号纳入变分约束框架，表现出更好的噪声鲁棒性。通过对模型收敛条件的合理控制，VMD方法的能够有效分解中心频率和各模态。

图1 VMD分解算法流程图

3 形态学分形理论

数学形态学以积分几何、集合论、拓扑学为依托的交叉综合学科，对于信号来说，采用数学形态学进行几何结构的探寻，然后使用集合论定量描述信号。实质上，数学形态学是对信号的几何结构和形状进行测定，故称之为形态学。

3.1 形态学概念

腐蚀、膨胀、开运算与闭运算是形态学的基本操作，一维离散信号f（n），F=｛1，2，K，N｝，结构元素g（m），G=｛1，2，K，M｝，且M＜＜N。则f（n）关于g（m）腐蚀和膨胀的运算过程如下[3]

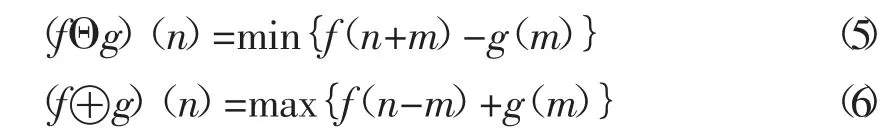
式中，m∈G。

腐蚀和膨胀计算的核心原理是通过逐点平移结构元素，搜寻结构元素原点和待分析信号的重合位置。当结构元素原点与待分析信号在某一点重合时，将落在G内的待分析信号幅值和结构元素幅值相减（相加），取计算结果的最小（最大）值，其结果即为在该点的腐蚀（膨胀）运算结果。

f（n）关于g（m）开和闭运算

符号Θ、⊕、o、·依次表示腐蚀运算、膨胀运算、开和闭运算。

3.2 形态学分形理论

常见的形态学分形维数有盒维数、信息维数、关联维数等。盒维数因其能从整体上反映整个系统的动态结构变化而受到广泛应用。这里对盒维数的计算方法进行说明，盒子维数一般记为DB。

盒子维数实质是对于一个图形，可以用长为的正方体“盒子”进行覆盖，当长度不断减小直至为零，最终确定完成覆盖图形的正方体“盒子”数目N，同时要保证数目最少。盒子维数计算方法简单，在实际问题中的应用较为广泛，但是由于在计算时，需要对划分网格、参数和算法估计等进行规则化，导致计算繁杂且结果不准确。为解决此类问题，本文提出了形态学分形估计信号的分形维[4]，这里给出分形维的计算过程。

（1）形态学单一分形维数估计

对于给定信号f（n），n=1，2，K，N，定义其在给定尺度下的结构元素定为：

式中g——单位结构元素

ε——给定尺度

则尺度ε对信号的覆盖面积可以表示为

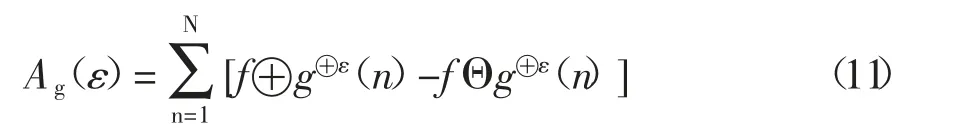
且Ag（ε）应满足下列条件

其中，ε=1，2，…，εmax；DM是信号的Minlowski-Bouligand维数，c为常数，故

（2）形态学广义分形维数估计

形态学单一分形维数是一种特殊的形态学广义分形维数，形态学广义分形维数从多个测度出发，更全面的描述状态信号的分形特征。其计算步骤如下

（a）分布函数计算

式中，f⊕εg（n）和fΘεg（n）指的是多尺度下信号的膨胀和腐蚀，f⊕εg（n）-fΘεg（n）即为膨胀与腐蚀之差。式（14）中引入ui（ε）的目的是给出一个局部度量的分布函数，来描述信号差异的分布情况。同时，ui（ε）的高阶矩表现出信号在尺度上的不均匀性。

（b）计算形态学广义信息熵Kq（ε）

（c）计算分形维Dq

实际运算过程中，广义分形维数是通过Kq（ε）和ln（ε）最小二乘法拟合得到的。

3.3 形态学分形维数的参数选择

形态学分形维估计算法中主要影响参数为单位结构元素g和最大尺度εmax[5]。根据文献[6]的分析，随着εmax的增大，计算精度会增加，但也会导致循环次数增多，计算时间无限加长。因此，根据经验最大尺度εmax=100。

根据文献[7]，因扁平结构元素g与复杂信号的结构最接近，且计算快捷准确，同时避免信号幅值对形态学分形维数的影响，故选择扁平结构元素g作为本文往复压缩机振动信号的单位结构元素。然而，形态学分形维数的大小随扁平结构元素g的长度而变化，所以应对扁平结构元素g的总长度进行优化选择。本章以往复压缩机气阀状态振动信号为主要研究对象，图2为压缩机气阀正常和故障状态下形态学分形维数随结构元素长度变化曲线。从图2中可以看出，结构元素长度N与形态学分形维数的数值存在依赖关系，直接影响计算准确性。通过4条曲线的交叠情况可以看出，结构元素长度N在[10，30]之间时，4种状态的形态学分形维数可以区分开。所以结构元素长度N=20。

随结构元素长度变化曲线

4 基于变分模态分解与形态学分形的往复压缩机故障诊断应用

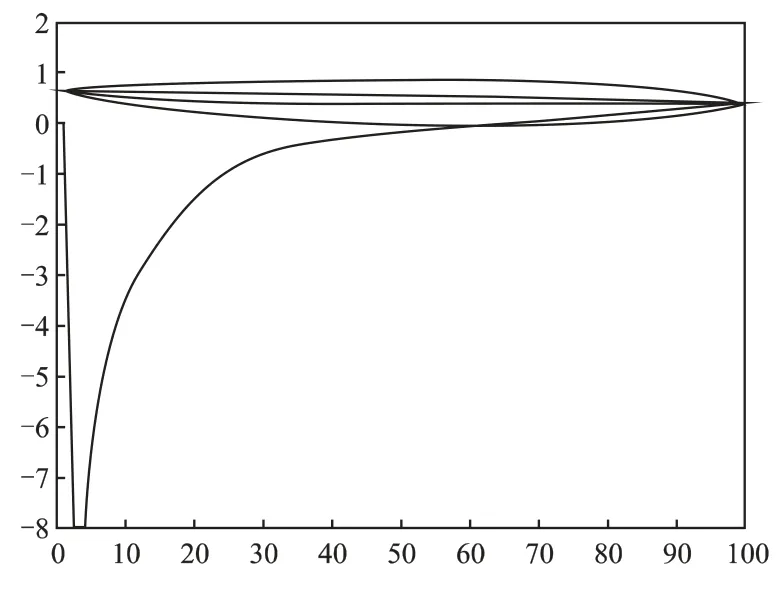
图2 气阀正常和故障状态下分形维数随结构元素长度变化曲线

本部分通过建立往复压缩机故障模拟试验平台，采用试验数据对上述研究成果进行验证。研究对象为2D12型往复压缩机，收集其在不同工况下的监测信号，利用变分模态分解与形态学分形方法进行特征提取，利用支持向量机（SVM）对往复压缩机故障进行识别，并对识别结果进行分析并与利用常规经验模态分解（EMD）方法进行特征提取所得的结果进行对比，结果如表1所示。

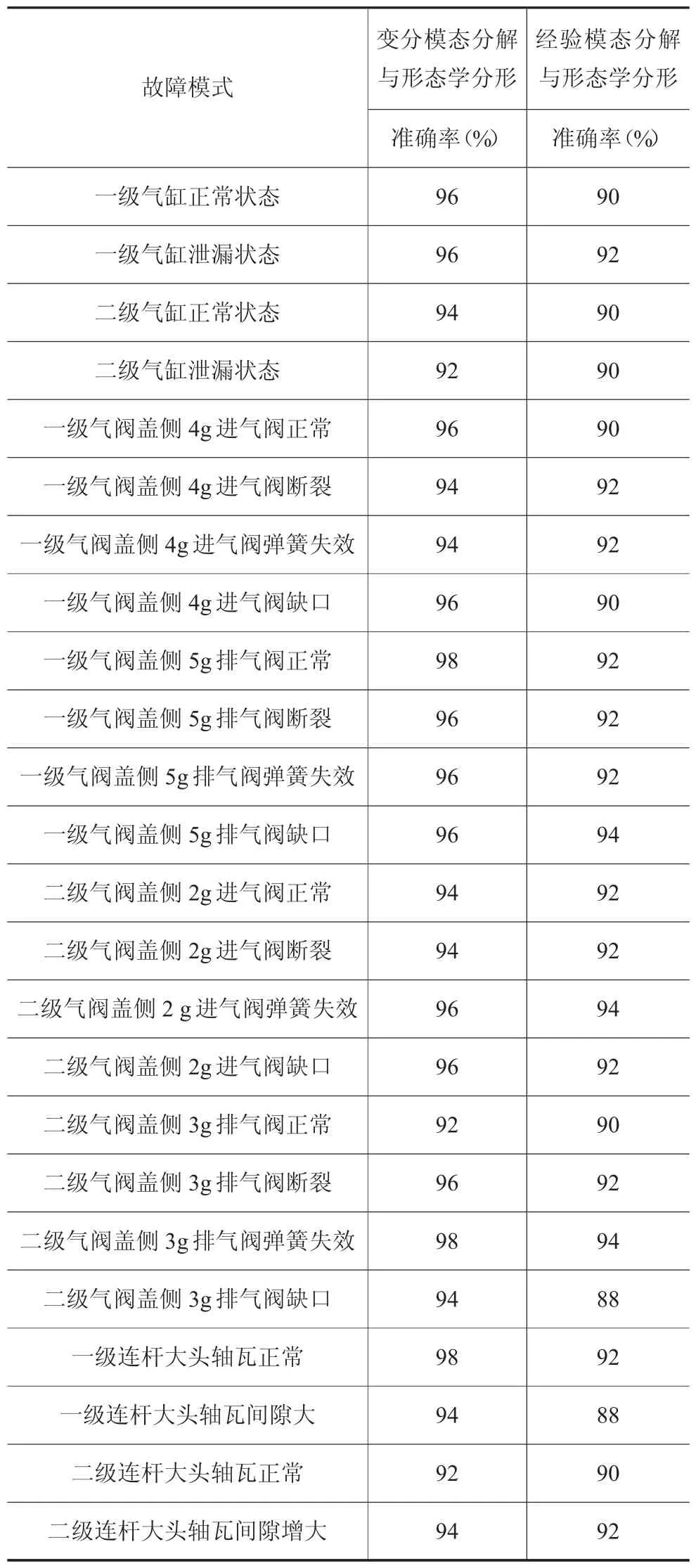
表1 基于变分模态分解与形态学分型的特征提取方法的故障识别准确率

通过以上识别结果可知，基于变分模态分解与形态学分形的特征提取方法明显优于EMD与形态学分形方法。其主要原因是利用较为简单的“数盒子”原理进行计算时，需要对划分网格、参数和算法估计等进行规则化，导致计算过程繁杂计算结果不准确的局限。本文提出的形态学分形的方法避免了计算过程繁杂计算结果不准确的现象，显著提高了算法准确性，具有更高的识别准确率，可以有效地诊断出往复压缩机的不同故障。

5 结论

针对往复压缩机振动信号的非线性、非平稳特性，本文提出了基于变分模态分解与形态学分形的往复压缩机故障诊断方法，通过分析往复压缩机典型故障与振动响应间的关系，建立了有效的滑动轴承和气阀故障诊断框架，基于多源监测信号，结合机器学习方法，对往复压缩机的常见故障进行了诊断。该方法有利于提高往复压缩机关键部件故障诊断的准确性，并为往复压缩机长周期安全运行和维修决策提供依据。