基于RBF神经网络模型的车门多目标轻量化设计

李 军，冷 川

(重庆交通大学 机电与车辆工程学院，重庆 400074)

0 引 言

车身的轻量化已经成为研究热点。车门是车身的重要组成部分，车门的轻量化应当在满足刚度、强度和模态性能要求下进行。朱茂桃等[1]应用Kriging构建近似模型方法及序列二次规划法对车门进行优化，不仅提高了车门刚度和模态性能，还减少了质量；方拓林等[2]采用拉丁超立方方法和响应面方法，考虑车门的一阶频率、侧向刚度、垂直刚度、侧面碰撞多种工况，对车门进行了多目标优化；马彬彬等[3]采用径向基函数神经网络构建近似模型方法和模拟退火算法，考虑车门抗凹刚度和下垂刚度工况下，提高车门性能的同时，实现了减重；高云凯等[4]采用Kriging构建近似模型方法和响应面方法，考虑车门下沉刚度、窗框刚度及塑性变形量工况下，对车门进行多目标轻量化设计；秦训鹏等[5]采用灵敏度方法和响应面法，构建车门模态频率的响应面优化模型，改善车门模态性能的同时实现了车门的减重。

通过以上车门轻量化研究得知，通过试验设计分析确定关键零件厚度为优化设计变量，考虑车门多个刚度工况和前两阶模态频率，使用RBF神经网络方法构建多个响应的近似模型来进行多目标优化的研究较少。因此，笔者采用试验设计方法将影响车门刚度、模态及质量的关键零件作为设计变量，然后进行哈默斯雷(Hammersley)试验设计得到样本点数据，用径向基函数(radial basis function，RBF)神经网络模型拟合车门的刚度、模态及质量的近似模型，并使用多目标遗传算法寻优，在满足车门性能要求下，实现车门的减重。

1 车门结构分析

1.1 车门模型的建立

车门主要由车门内外板、内外板加强板、防撞梁和连接板等部件组成，其由厚度不同的薄板冲压焊接形成，其长度和宽度方向尺寸远大于厚度方向尺寸，所以对车门主要采用壳单元进行离散化[1]。笔者在前处理软件HyperMesh中构建车门结构有限元模型，考虑到计算精度和时间，网格单元大小设为10×10 mm。同时针对单元的参数控制，焊点采用acm单元模拟，粘胶用adhesives，螺栓连接用 rigid刚性单元模拟。车门部件使用同一种材料，弹性模量为210 GPa，泊松比为0.3，密度为7 850 kg/m3。

最终车门有限元模型中壳单元个数为47 477，节点数为48 338，其中四边形单元个数为42 343，三角形单元个数为2 961，三角形单元所占百分比为6.2%，小于8%，符合建模要求，模型质量为23.394 kg。

在前处理软件HyperMesh中分别建立车门的上扭转刚度、下扭转刚度、侧向弯曲刚度、下沉刚度和自由模态5种分析工况，通过求解器软件OptiStruct求解。

1.2 车门刚度分析

1.2.1 车门扭转刚度工况

车门的扭转刚度是指车门抵抗扭转力下的变形能力，主要包括上扭转刚度和下扭转刚度[3]，影响着车门的密封性、振动及零件受损等问题。

上扭转刚度工况设置为：约束车门上下铰链位置的6个自由度和门锁位置的3个平动自由度，在车门窗框的后下方位置施加900 N的力，方向由车门内指向车门外。下扭转刚度工况的约束方式同上扭转刚度工况一致，加载力位置在车门后下方的内板圆角处，力的大小为900 N，方向为车门内指向车门外，如图1。

通过OptiStruct求解，得出车门上扭转的加载点位移为3.834 mm，车门下扭转的加载点位移为2.744 mm，均小于要求加载点的位移上限6 mm，满足要求。

1.2.2 车门侧向弯曲刚度工况

车门的侧向弯曲刚度是指车门抵抗施加于车门主平面垂直方向载荷的变形能力。如果车门侧向弯曲刚度不足，在车门以较大的力关闭时会导致车门弯曲变形。其工况设置为：约束车门上下铰链位置的6个自由度和门锁位置的3个平动自由度，在车门后上方位置施加200 N的力，方向为车门内指向车门外。

通过OptiStruct求解，得出车门侧向弯曲的加载点位移为2.801 mm，小于要求加载点的位移上限6 mm，满足要求。

1.2.3 车门下沉刚度工况

车门的下沉刚度是指车门抵抗自身重力和铅锤方向载荷的变形能力，直接影响到车门与侧围之间的间隙大小。其工况设置为：约束车门上下铰链位置的6个自由度和门锁位置的车门绕铰链轴线的转动自由度，在车门锁位置施加900 N的力，方向为竖直向下[6]。

通过OptiStruct求解，得出车门下沉刚度工况的加载点位移为2.964 mm，小于要求加载点的位移上限6 mm，满足要求。

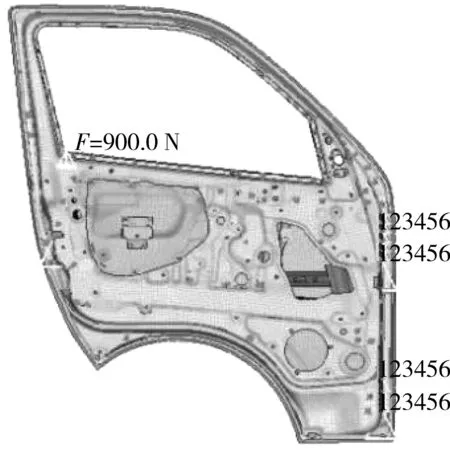
图1 车门上扭转刚度工况Fig. 1 Condition of upper torsion stiffness of the door

1.3 车门模态分析

通常对车门结构进行自由模态计算，车门结构的低阶模态频率和相应振型对结构动态特性影响较大[7]，所以通过OptiStruct作自由模态分析，在后处理软件HyperView中查看结果，同时提取前两阶模态频率，分别为42.98、47.03 Hz，均分别大于企业要求的30、35 Hz，满足要求，且还有富余。

2 车门设计变量的选择确定

2.1 部分因子试验设计

试验设计(design of experiments，DOE)作为近似模型的一种采样策略，主要有全因子试验设计、部分因子试验设计、拉丁超立方试验设计及哈默斯雷(Hammersley)试验设计等。部分因子试验设计是选取全因子设计的一部分，可以减少试验次数。对于一个每个因素为两水平的部分因子设计，其典型的试验次数为全因子试验数的2-p，p为正整数。

2.2 设计样本点采样及试验结果分析

整个车门零件较多，每个零件对车门刚度和模态性能影响不同，因此先初步选择车门零件作为样本点采样的设计变量，通过部分因子试验设计筛选出影响较大的设计变量作为后续优化模型的变量。

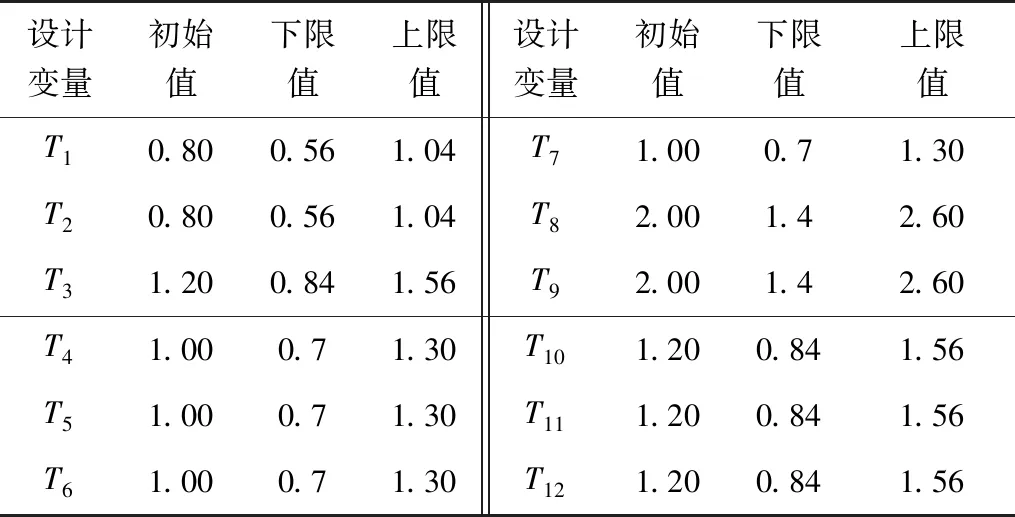
设计变量位置如图2，其中零件序号1～12分别为外板、内板、内板加强板、外板加强板、玻璃前导轨、玻璃上导轨、玻璃后导轨、防撞梁1、防撞梁2、连接板件1、连接板件2、连接板件3。T1～T12分别为序号1～12的零件厚度，其变化范围为原始厚度的±30%，各设计变量的初始值和变化范围见表1。

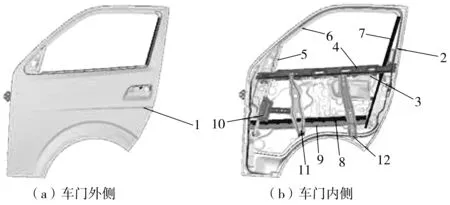
图2 车门初始设计变量位置Fig. 2 Initial design variable position of door

mm

通过有限元优化软件HyperStudy，以初选的12个车门厚度作为设计变量，以车门的上扭转工况下的加载点位移d1、下扭转工况下的加载点位移d2、侧向弯曲工况下的加载点位移d3、下沉工况下的加载点位移d4、车门的一阶模态频率f1、二阶模态频率f2及质量m为响应函数。采用部分因子试验设计进行12因素3水平的试验设计，各个设计变量的高水平取上限值，低水平取下限值，中水平取初始值，采样27组数据。

为获得每个设计变量对各个响应的影响大小，处理数据时，通过计算每个设计变量对各个响应的线性主效应[8]，其绝对值越大，影响也越大，记Em、Ef1、Ef2、Ed1、Ed2、Ed3、Ed4分别代表车门零件厚度对响应m、f1、f2、d1、d2、d3及d4的线性主效应，计算结果见表2。

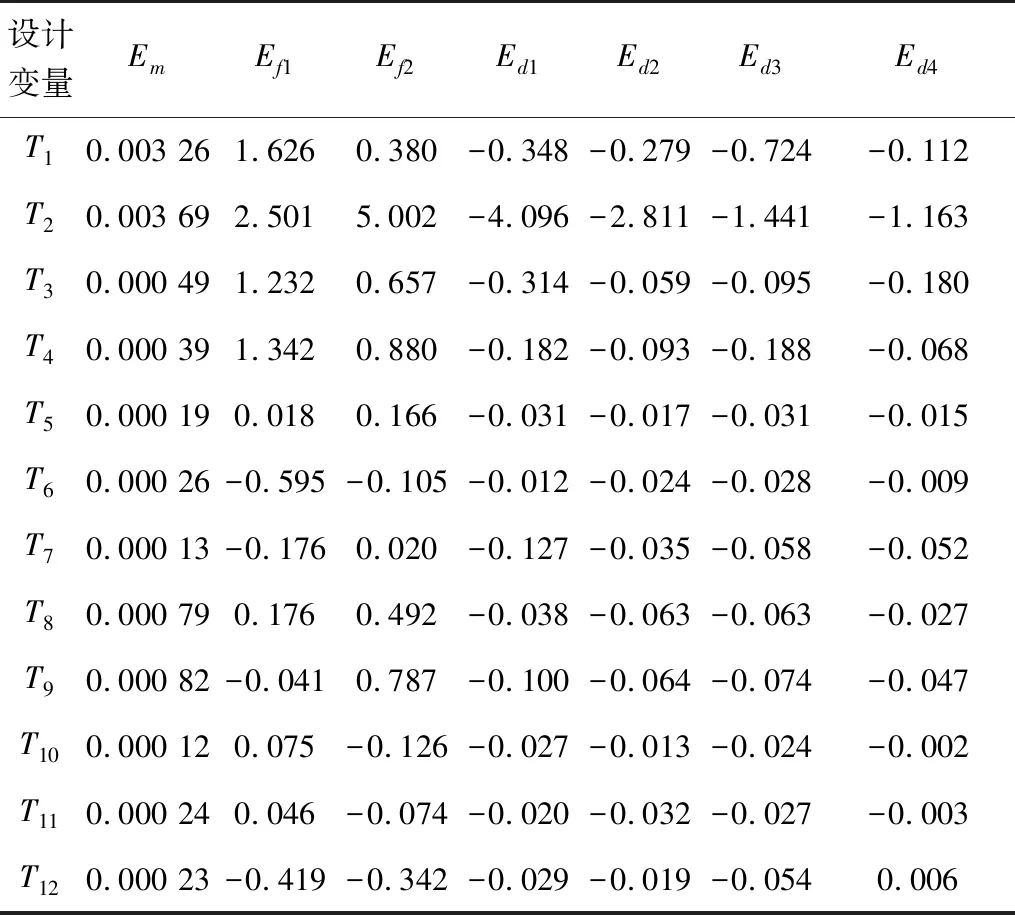
表2 设计变量对响应函数的线性主效应Table 2 Linear main effect of design variables on response function

分析表2可知：对前两阶模态频率影响较大的板件是T1、T2、T3、T4、T12；对质量影响较大的板件是T1、T2、T3、T4、T8、T9；对d2、d3影响较大的板件是T1、T2、T3、T4、T8、T9；对d1影响较大的板件是T1、T2、T3、T4、T7、T9；对d4影响较大的板件是T1、T2、T3、T4、T7、T8、T9。因此，最终选取T1、T2、T3、T4、T8、T9、T12为后面优化模型的设计变量。

3 RBF神经网络模型

3.1 哈默斯雷(hammersley)试验设计

为了建立车门质量、刚度及模态性能的近似模型，需要进行试验设计来获取样本点。常用的试验设计方法有拉丁超立方试验、中心复合试验及哈默斯雷试验等。哈默斯雷试验采样属于类蒙特卡洛方法，基于哈默斯雷点，该算法采用伪随机数值发生器，均匀地在一个超立方体中进行抽样，其采样的因素水平为任意水平，其采样的试验点均匀性优于拉丁超立方采样[9]，其样本分布对比如图3。

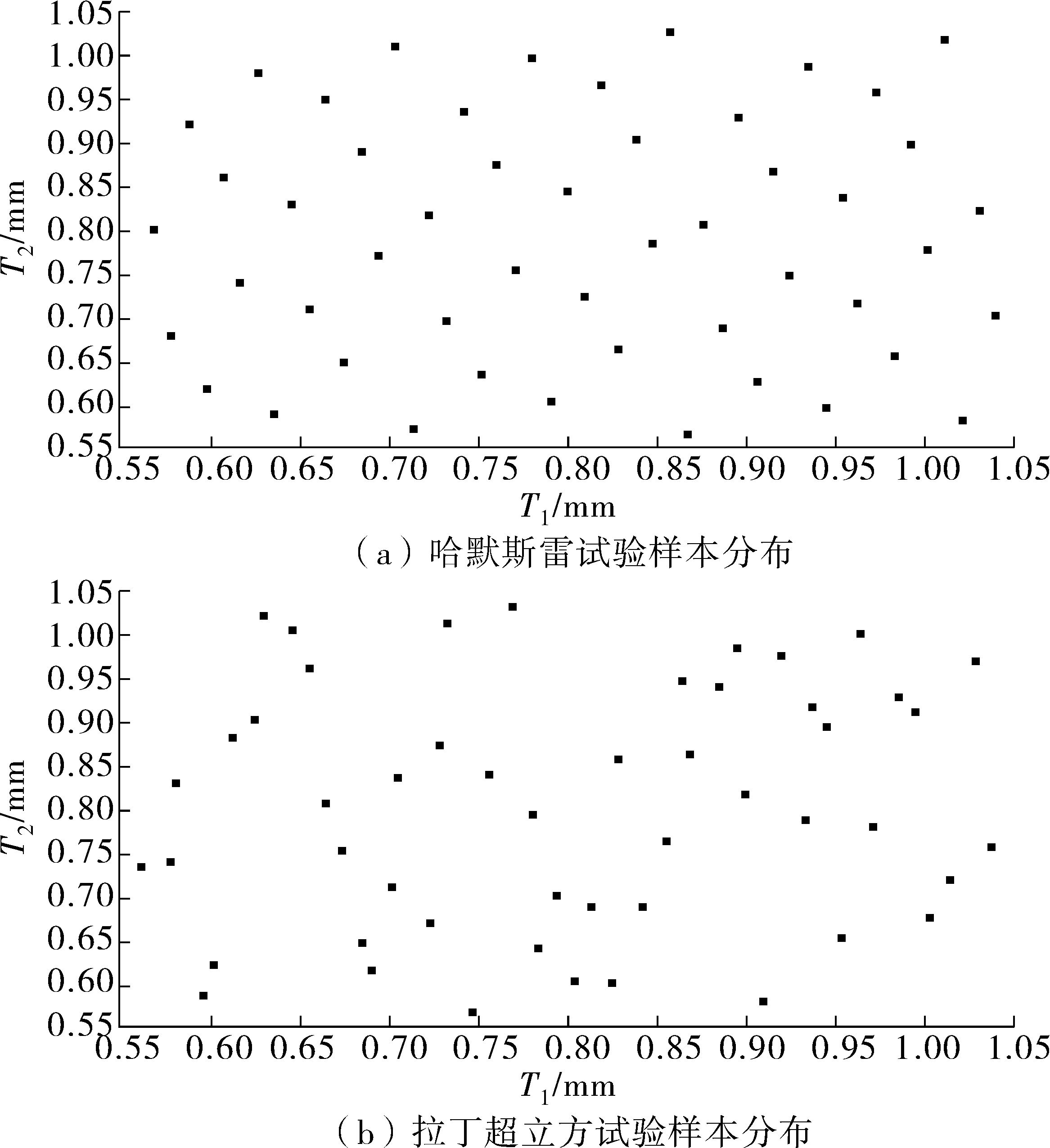
图3 试验样本分布对比Fig. 3 Distribution comparison of test samples

在优化软件HyperStudy中，以T1、T2、T3、T4、T8、T9、T12为设计变量，取值范围为原始厚度的±30%，详见表1。以d1、d2、d3、f1、f2、m为响应，采用哈默斯雷试验设计，其中因素为7个，水平为50，得到50组样本数据。

3.2 RBF神经网络模型的构建

常用的结构优化近似模型中有响应面模型[10]、Kriging模型[11]以及径向基函数模型[12]等。径向基函数(radial basis function，RBF)神经网络模型是一种利用离散多元数据拟合未知函数的方法，作为近似模型，其具有良好的非线性逼近性，在收敛的情况下，有收敛快、计算稳定等优点。

在RBF神网络模型中，假设x1,…,xN∈Ω⊂RN为一组已知的输入向量，即设计变量，y1,…,yN∈R为对应的已知的输出值，即性能响应值。基于径向基函数，用于近似估计未知点的差值模型F(x)可表示为：

(1)

式中：αj为径向基函数差值模型系数，在建立神经网络模型过程中，由样本点数据求解得到。具体求解式为式(2)、式(3)定义的N+1个线性方程，通过求解此N+1个线性方程可得到N+1个未知系数。

(2)

(3)

式中：gj(x)=g(‖x-xj‖c),j=1,…,N为一组径向基函数；‖x-xj‖为待测点与样本点的欧几里得距离；c为样条形状参数[3]。

使用哈默斯雷试验设计采样的50组样本数据，采用RBF神经网络模型拟合车门质量、一阶和二阶的模态频率、上扭转刚度、下扭转刚度、侧向弯曲刚度及下沉刚度的近似模型，其中T1和T2的车门上扭转刚度响应的RBF神经网络模型如图4。

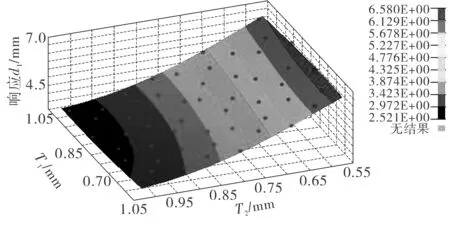
图4 T1和T2的车门上扭转刚度响应近似模型Fig. 4 Approximate model of upper torsion stiffness for T1 and T2

近似模型的精确度对优化结果的可信度很重要。笔者采用方差分析中的参数决定系数R2对模型的精确度评价，R2的取值范围为0～1，其结果越接近1，说明精度越高[13]。在设计空间重新生成10个样本点进行拟合模型的精度检验，各拟合模型精度见表3。

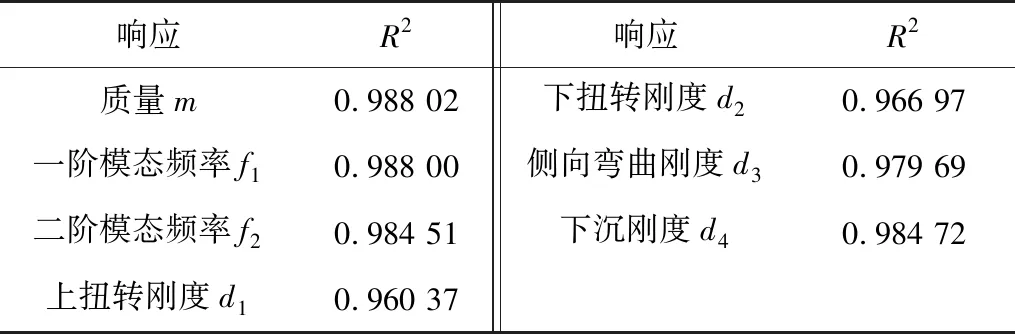
表3 RBF拟合模型的精度评价Table 3 Accuracy evaluation of RBF fitting model

由表3可知，用RBF神经网络模型构建的近似模型的R2均很接近于1，说明构建的近似模型满足精度要求，可以作为优化模型。

4 车门多目标优化及结果分析

4.1 多目标优化模型

根据所选定的车门7个关键零件厚度为优化的设计变量，即T1、T2、T3、T4、T8、T9、T12，变化范围为各部件原始厚度的±30%，详见表1。在合理的范围内，车门优化要求：以车门的质量最小和一阶模态频率最大为优化目标，二阶模态频率和刚度性能指标为约束，数学模型如式(4)：

(4)

式中：TiL、TiU分别为设计变量的下限值和上限值；i=1，2，3，4，8，9，12。

4.2 优化结果分析

在软件HyperStudy中，基于第3节建立的RBF神经网络模型作为近似模型，采用多目标遗传算法求解多目标优化模型。多目标遗传算法参数为：整个种群数目大小为114，最大迭代数为50，突变率为0.01，精英群体所占比例为10%。通过迭代计算，得到Pareto前沿解集，如图5。

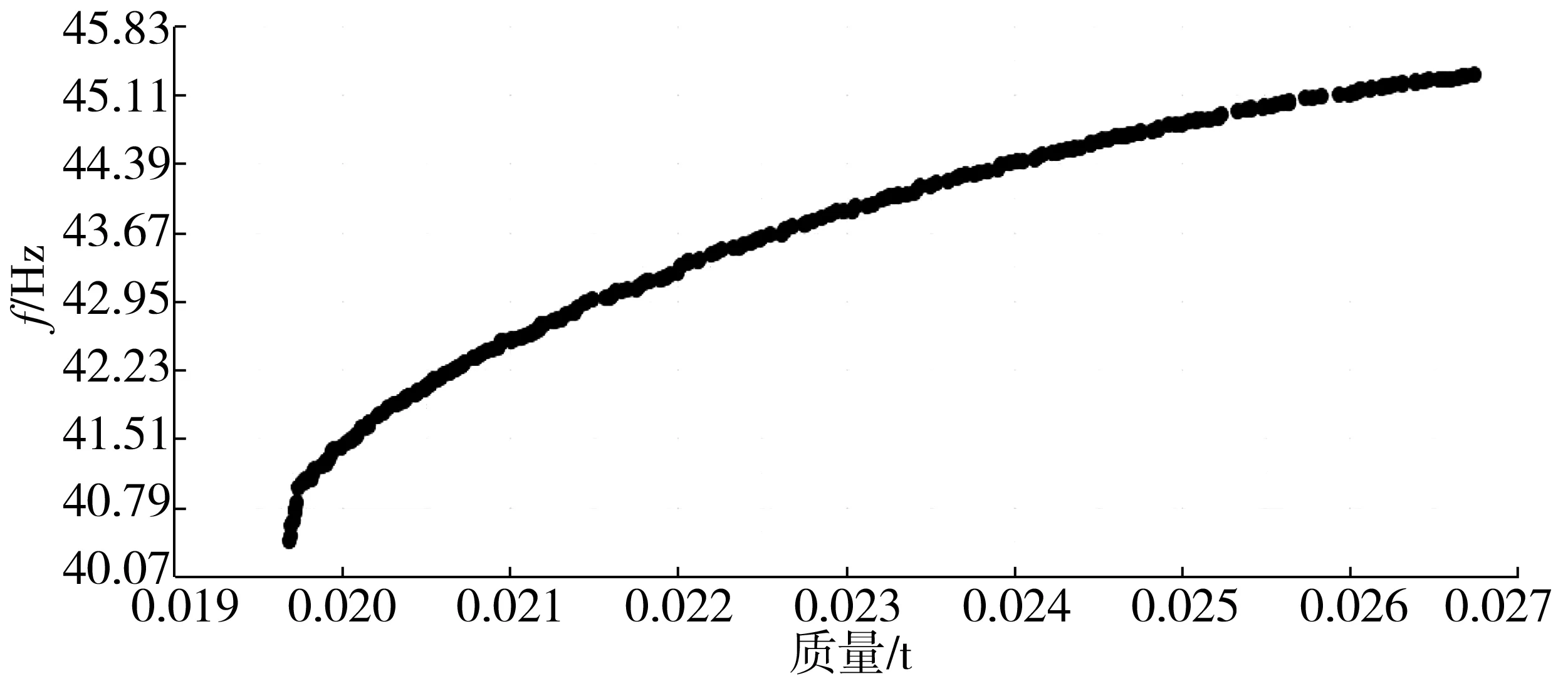
图5 Pareto前沿解集Fig. 5 Pareto front solution set

从所得的Pareto前沿解集中选取合适的解作为最优解，在原始模型中修改优化设计变量的数值，其他保持原始数值，将其带入有限元模型中进行求解，将其结果与优化解进行对比，误差均在2%以内，说明寻求的最优解合理。再将最终优化结果与原始模型比较可得，在车门刚度和一阶模态频率减少较小且满足要求的情况下，优化后车门比原车门质量减少了7.34%，见表4。

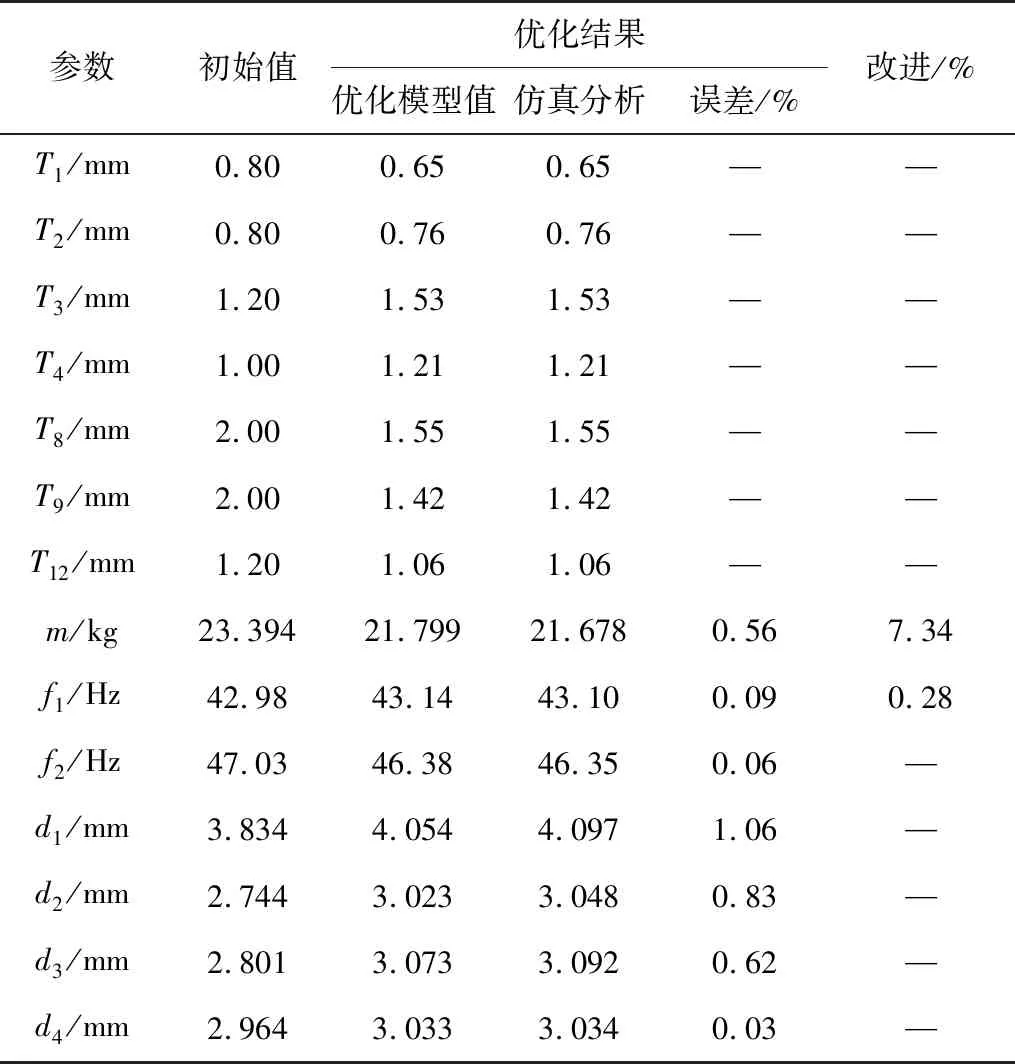
表4 车门优化前后性能参数Table 4 Performance parameters of door before and after optimization

5 结 语

在车门轻量化设计中，对车门进行试验设计以找到影响车门质量、刚度和模态性能的关键零件，并将其作为优化的设计变量；结合哈默斯雷试验设计法，构建车门质量、一阶模态频率、二阶模态频率、车门的上扭转刚度、下扭转刚度、侧向弯曲刚度及下沉刚度RBF神经网络近似模型。在近似模型的基础上，考虑车门质量、刚度和模态性能的几个主要指标下，通过多目标遗传算法寻优计算，从得到的Pareto前沿解集中选取一个合适的解作为最优解，可验证其有效性。通过优化设计，在车门刚度和模态各性能满足要求情况下，车门的质量减少了7.34%。将试验设计方法和基于RBF神经网络近似模型的优化相结合，不仅提高了优化效率，还保证了计算精度。