考虑荷载影响面的钢桥面板顶板-U肋焊缝疲劳损伤分析
吉伯海,徐 捷,姚 悦,傅中秋
(河海大学 土木与交通学院,江苏 南京 210098)
0 引 言
随着我国交通基础设施建设需求的不断提升,作为钢结构桥梁主要桥面系形式之一的正交异性钢桥逐渐得到了广泛应用。根据相关研究和实桥检修结果发现[1-4],由于构造、焊接残余应力等缺陷,钢桥面板的顶板-U肋连接焊缝处在车轮荷载长期交变作用下易产生疲劳损伤。根据裂纹的起裂位置,连接焊缝处疲劳裂纹大致可划分为焊根裂纹和焊趾裂纹[5,6]两类,其危害不容忽视,尤其是焊根裂纹,这类裂纹往往贯穿顶板或焊缝后才得以发现,而此时,裂纹已大大削弱了顶板-U肋连接细节的正常工作性能。目前,轮载横向位置对焊根裂纹及焊趾裂纹的具体作用尚不明确,故有必要研究轮载作用位置对两类裂纹疲劳损伤的影响。此外,我国JTG D 64—2015《公路钢结构桥梁设计规范》(以下简称《规范》)给出的钢结构桥梁疲劳荷载计算模型仅仅是四轴车的单车模型,且设计偏于安全。根据吕磊等[7]对某大桥实际交通流量的统计,二轴货车数量占货车总数高达45.7%,其对疲劳细节的影响不容忽视。
吉伯海等[8]及K. KWON等[9]的研究表明,桥梁的应力-时程曲线具有一定的周期性。笔者据此简化有限元模型,以钢桥面板节段模型横隔板处的顶板-U肋连接焊缝附近局部区域为研究对象,采用两点热点应力法对比分析了该区域焊根和焊趾在二轴货车荷载加载下的应力分布特征;利用疲劳损伤度计算分析了易导致焊根和焊趾疲劳损伤的轮载作用位置;研究了过焊孔构造细节对顶板-U肋连接焊缝处疲劳损伤的影响;分析了考虑轮迹横向分布概率后的疲劳损伤结果。研究结果可为实桥顶板-U肋连接焊缝疲劳损伤研究提供依据。
1 有限元模型
为模拟正交异性钢桥面板顶板-U肋连接焊缝附近的实际应力分布,利用ANSYS建立钢桥面板节段模型,如图1(a)。取横桥向7个U肋和纵桥向5个横隔板(即一个完整车道)作为模型整体尺寸依据。具体模型如下:顶板厚度为12 mm,单个完整U肋板的长×高×厚=300 mm × 280 mm × 6 mm,横隔板上过焊孔半径为35 mm,顶板与U肋的夹角为78°。相邻横隔板间距为3.2 m,模型所采用单元类型均为SHELL63壳单元,模型整体网格划分尺寸为64 mm,针对顶板和U肋接缝处进行局部网格细化操作,如图1(b)。

图1 有限元模型Fig. 1 Finite element model
为模拟实桥中钢桥面板的受力特点,模型边界约束如下[10]:针对5片横隔板竖向末端约束竖向和纵桥向2个方向的平动自由度和转动自由度,针对模型与横桥向平行的两边顶板施加竖向平动约束和绕竖轴和横轴转动约束,在与纵桥向平行的顶板边界限制其竖向平动。在上述边界条件下,根据圣维南原理,只要研究位置距边界一定距离,即可保证计算结果不会与实桥测算数据产生较大偏差。
按照疲劳损伤等效原理求出二轴货车车轮荷载模型,车辆前轴轴重为30 kN,前轮着地面积为200 mm × 300 mm,后轴轴重为55 kN,后轮着地面积为200 mm × 600 mm。加载方式如图2,e为轮载中心线距U肋横向中轴线距离,e=n×150 mm(n为正整数),即以轮载中心线每移动150 mm作为一个加载工况。


图2 加载工况Fig. 2 Loading cases
考虑到模型的对称性和荷载横向有效宽度,笔者仅以中间号U肋为研究对象,轮载中心线向横向一侧移动,共11种工况。提取顶板-U肋连接焊缝处热点应力,文中所提取的热点应力为国际焊接学会所推荐的两点应力取值。
2 影响面计算分析
2.1 应力分析
图3为车轮位于不同横向位置时,顶板-U肋连接焊缝处的应力在前轮和后轮分别作用下的分布情况。无论是前轮还是后轮作用,顶板-U肋连接焊缝附近热点应力几乎始终保持压应力σc或极小拉应力σt(σt﹤0.2 MPa)。

图3 车轮不同横向距离下连接焊缝应力分布Fig. 3 Stress distribution of weld joints with different transverse positions of wheels
由图3可见:
1)在偏移值e=0处,顶板-U肋连接焊缝处应力达到最大值,随着车轮横向位置逐渐偏离U肋正上方,应力逐渐下降。
2)当e=0~450 mm,测点应力对车轮的横向作用位置比较敏感,应力值均下降较快,且前轮下降速度相对更快。
3)当e≥750 mm,无论是前轮还是后轮作用,应力基本趋于0:前轮作用在e=750 mm处,应力值为0.131 MPa,相较于e=0处(应力-30.487 MPa)降低了99.57%;后轮作用在相同位置处应力降低了99.02%。因此,可认为前、后轮在顶板-U肋连接焊缝处产生的应力的横向影响范围均为750 mm。
4)在顺桥向方向上,横隔板处两侧的应力随着车轮远离横隔板而迅速降低,在到达前、后相邻两横隔板前,应力已几乎降至0。因此,可认为车轮荷载作用于横隔板处对顶板-U肋接缝的纵向影响长度约为6.4 m,即约2个横隔板的间距。
2.2 应力幅分析
不同车轮横向位置下顶板-U肋连接焊缝处应力幅σr如图4。
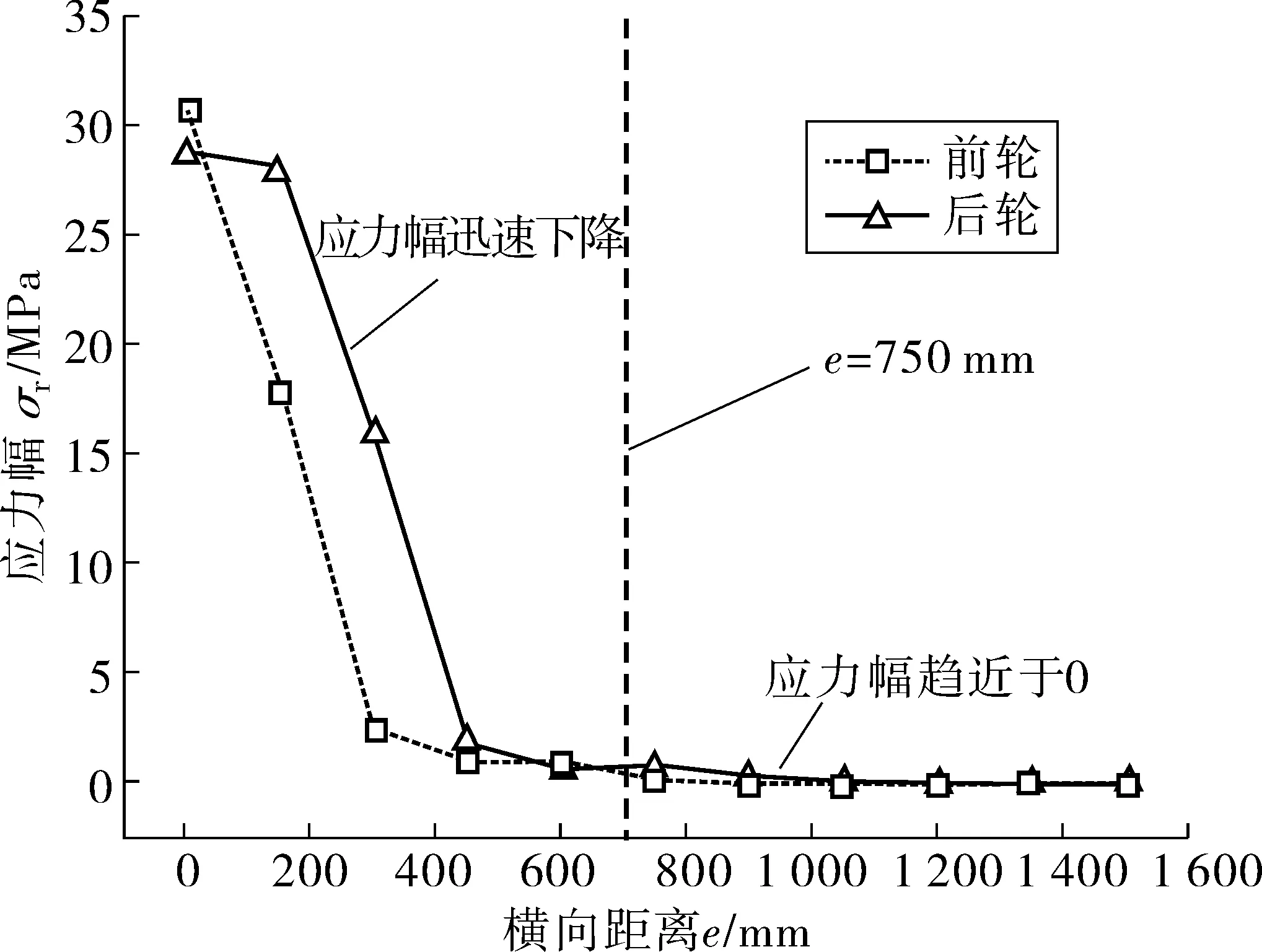
图4 车轮在不同横向距离e处连接焊缝的应力幅σrFig. 4 Stress range σr of weld joints with different transverse positions of wheels e
由图4可见,随着车辆横向偏移值e的增大,顶板-U肋连接焊缝处的应力幅σr呈下降趋势,得到以下结论:
1)前、后轮产生的最大应力幅σr,max:在e=0处,分别为30.7、28.7 MPa;在e=300 mm处,分别为2.54、15.89 MPa,降幅分别为91.73%、44.63%;在e=450 mm处,分别为0.97、1.96 MPa,降幅分别为96.84%、93.17%。
2)在e=750 mm处,前、后轮导致的应力幅已基本趋近于0,即当e≥750 mm时,应力幅逐渐趋于稳定,并保持在0附近。车辆对顶板-U肋接缝处的疲劳损伤可不予考虑。因相邻两车道间距约为1.75 m,故可不考虑其它车道车辆的干扰。同时,顶板-U肋接缝的纵向影响长度约为6.4 m,可认为顶板-U肋处的影响面为750 mm × 6 400 mm。
3 顶板-U肋接缝疲劳损伤分析
3.1 应力-时程曲线
利用二轴车对模型进行加载,考虑所研究的顶板-U肋接缝的应力横向影响范围,选取车辆横向偏移值e=0~750 mm,得到单车行驶下顶板-U肋连接焊缝焊根和焊趾的应力-时程曲线,如图5。

图5 顶板-U肋连接焊缝处应力-时程曲线Fig. 5 Stress-time history curves at weld joints of rib-to-deck connection
从图5可以看出,焊根和焊趾处的应力变化规律相似,即:
1)在车辆纵向移动过程中,当车轮距测点区域较远时,焊根和焊趾处应力较小,基本接近于0。
2)随着车轮逐渐靠近测点,拉应力数值逐渐增长,当车轮经过焊缝正上方时,应力产生突变,由拉应力迅速转变为较大的压应力或较小拉应力。
3)当车轮再次远离焊缝,测点应力又迅速恢复,构成了一个“拉-压-拉”应力循环。
4)每一车轴对应一个应力峰值,且后轮对应的应力峰值更大;同一轴上,焊根处应力峰值更大。
3.2 疲劳损伤度D
为了更加直观地分析顶板-U肋连接焊缝的焊根和焊趾在二轴车车轮荷载不同横向位置作用下的疲劳损伤差异,依据《规范》计算各疲劳部位的单日疲劳损伤度。《规范》规定σr-N(即:S-N)符合式(1)关系:
(1)
式中:Δσr为实际作用应力幅,MPa;NR为Δσr对应的循环次数,次;Δσc为经历常幅荷载一定循环次数下的参考疲劳强度,文中Δσc=2×106MPa;m为参数,无量纲,根据构造细节划定的疲劳等级查阅《规范》得到,文中m=3。
根据图5应力-时程曲线,按式(2)计算各级应力幅Δσri下顶板与U肋连接焊缝的疲劳寿命Ni:
(2)
应力幅Δσri循环作用ni次引起的疲劳损伤如式(3):
(3)
根据Miner线性累计损伤理论,按式(4)计算车辆荷载在不同位置作用时,顶板-U肋连接焊缝各部位的标准损伤度D:
(4)
经式(1)~式(4)计算,得到在二轴车不同横向位置作用下焊根和焊趾处的疲劳损伤度D,见表1。
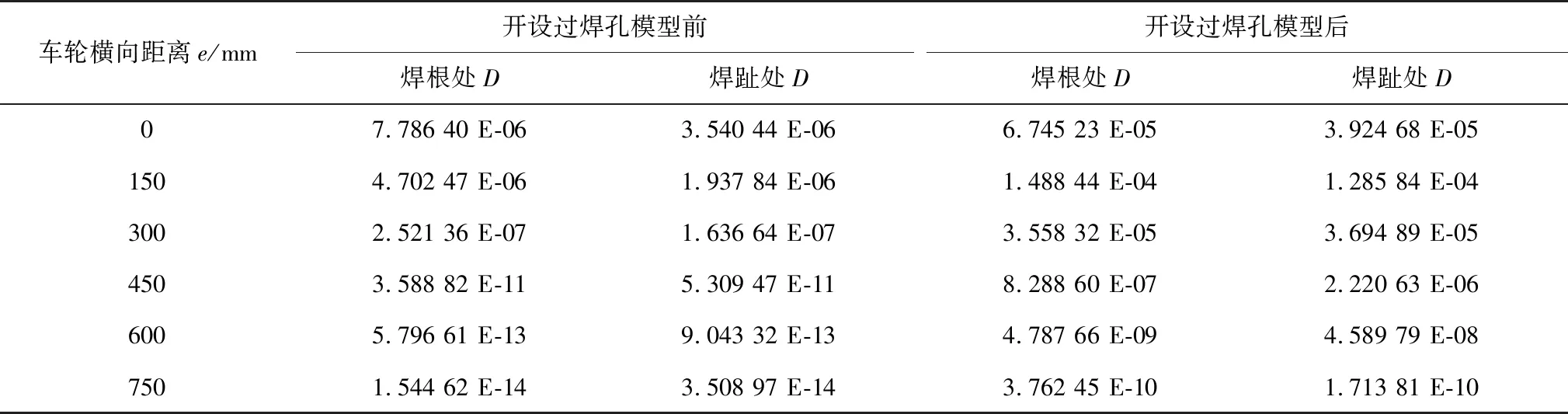
表1 开设过焊孔模型前、后顶板-U肋连接焊缝的疲劳损伤度DTable 1 Fatigue damage D of rib-to-deck weld joints in model with or without weld hole
由表1可见,顶板-U肋连接焊缝处焊根和焊趾的最不利荷载位置在e=150 mm处:
1)当车轮横向偏移值e=0~150 mm,焊根处疲劳损伤度明显高于焊趾处,约为焊趾处的1.16~1.72倍,即当车轮作用范围位于焊缝正上方时,同样是焊根处更易产生疲劳损伤。
2)当车轮横向偏移值e≥150 mm,随着e的增大,e对焊根和焊趾造成的疲劳损伤均呈下降趋势,但下降速率较为缓和。
3)当车轮横向偏移值e=300~600 mm,焊根和焊趾处的疲劳损伤度均有较大降幅,但此时车辆荷载造成的焊趾处疲劳损伤度已明显高于焊根处,焊趾处疲劳损伤度约为焊根处的1.04~9.59倍。
综上,当车轮长期作用于距U肋中心线450~600 m时,焊趾处的疲劳损伤需要引起重视。当e=750 mm时,焊根处疲劳损伤度再次高于焊趾处,但此处的疲劳损伤度已大幅减小。
3.3 过焊孔构造对疲劳损伤度的影响
目前,在正交异性钢桥面板中设置纵肋贯穿横隔板时,一般有横隔板在纵肋与面板接缝处开设过焊孔和不开设过焊孔2种形式。过焊孔构造会影响纵肋与面板接缝附近应力分布[11,12]。笔者针对在横隔板上开设过焊孔的有限元模型,计算得到焊根和焊趾处应力-时程曲线如图6。
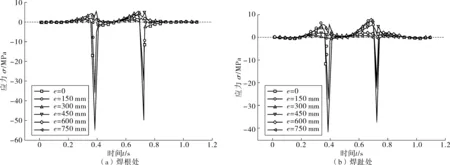
图6 开设过焊孔模型顶板-U肋连接焊缝处的应力-时程曲线Fig. 6 Stress-time history curves at weld joints of rib-to-deck connection with weld hole
由图6可见,相较于未开设过焊孔的模型,开设有过焊孔模型焊根和焊趾处的应力幅均较小,原因可能是过焊孔构造减小了该处顶板-U肋相对变形的限制,改变了顶板-U肋连接焊缝的局部刚度。开设过焊孔模型,当车轮荷载作用在不同横向位置e,顶板-U肋连接焊缝焊根和焊趾处的疲劳损伤度D计算结果见表1。由表1可见:
1)当e=0~300 mm,焊根处疲劳损伤度明显高于焊趾处,约为焊趾处的1.54~2.42倍,即当车轮作用范围位于焊缝正上方时,焊根处受到的疲劳损伤更严重。
2)随着车轮作用位置逐渐远离顶板-U肋连接焊缝正上方,焊缝处焊根和焊趾的疲劳损伤均呈下降趋势,且在e=450 mm处,疲劳损伤度出现陡降现象,此时前后轮均已基本偏离焊缝的正上方,可见顶板-U肋接缝处应力在车轮作用范围位于焊缝正上方时最为敏感。
3)当e=450~750mm,焊根和焊趾处的疲劳损伤度均已大幅降低,此时焊根处的疲劳损伤度已明显低于焊趾处,焊趾处疲劳损伤度约为焊根处的1.40~2.27倍。因此,当车轮长期作用于距U肋中心线450~750mm时,焊趾处的疲劳损伤往往更为严重。相较于未开设过焊孔的模型,在同一车轮位置作用下,开设过焊孔模型焊根和焊趾处应力下降,但疲劳损伤均有所升高,其中焊根处升高约18倍,焊趾处约升高36倍。
4 考虑影响面的疲劳损伤
4.1 轮迹分布概率模型
理论上,无外界环境干扰的情况下,车辆将严格按照车道中心线行驶[13],但行驶过程中由于车道断面形式、行车速度、实时交通情况等因素影响,车辆总会出现横向轨迹偏差。虽然有多种因素相互影响,但车辆的轮迹横向分布仍具有一定的规律,基本服从正态函数分布[14-16],为求得车辆轮迹横向分布疲劳计算模型,做如下2个假定:
1)各车道间车流互相独立不受干扰。
2)各车道车流的轮迹横向分布服从正态分布,即:
X~N(μ,S2)
(5)
设车道宽为3.75 m,减去标准车型轮距1.8 m,得到车道的有效宽度为1.95 m,故:
(6)
计算得标准差S=280 mm,则,最终轮迹分布模型为:
X~N(μ, 2802)
(7)
4.2 考虑轮迹分布概率的疲劳损伤评估
计算车道各部分车辆轮迹分布概率(仅计算0~750 mm),并将其转化为1(轮迹横向位置)×6(分布概率)的车轮轮迹横向分布概率矩阵[μ],如式(8):
(8)
根据表2中二轴车车辆作用下焊根和焊趾处的疲劳损伤度,以横向偏移位置为“行”,裂纹位置为“列”(第1列为焊根、第2列为焊趾),组成6 × 2的损伤度矩阵[w]:
(9)
按照式(10),将横向分布概率矩阵[μ]与损伤度矩阵[w]相乘,可得到考虑轮迹横向分布概率的损伤矩阵[S]:
(10)
由式(10)计算,可得考虑轮迹横向位置分布概率后的焊根处疲劳损伤度D=7.76E-05,焊趾处疲劳损伤度D=6.47E-05。
与没有考虑轮迹分布概率计算的的结果相比,考虑了轮迹分布概率后,焊根和焊趾处损伤度下降了69%,疲劳寿命得到显著提升。可见,受轮迹改变的影响,顶板-U肋连接焊缝处焊根和焊趾处疲劳寿命均比不考虑轮迹影响时要高。
《规范》给出了横向分布概率模型,但车轮横向分布范围仅考虑了最不利位置一侧0.25 m。笔者依据式(8)~式(10)提出一种新的轮迹横向分布概率模型,将横向分布范围扩大至750 mm。图7为两种方法示意。

图7 《规范》及笔者提出的轮迹横向分布概率法Fig. 7 The probability method of transverse distribution of wheel tracking in Specification and the method proposed by author
表2为根据《规范》和笔者提出的考虑轮迹分布方法分别计算所得的疲劳损伤度。可见:两者计算结果差异10%以上,与《规范》相比,笔者的方法更充分地考虑了轮迹横向分布的影响,计算所得的疲劳损伤更符合实际情况。因此,建议针对顶板-U肋连接焊缝处的疲劳损伤研究将车轮横向影响范围扩大至750mm左右。
5 结 论
通过建立钢桥面板节段模型分析了荷载影响面对顶板-U肋连接焊缝疲劳损伤的影响,重点探讨了车轮位于不同横向位置对焊缝附近应力分布,研究了过焊孔构造和轮迹横向分布概率对焊缝的疲劳损伤度的影响,并与《规范》中的计算方法进行了对比,得到以下结论:
1)车轮横向位置e对横隔板处顶板-U肋连接焊缝的疲劳影响显著,但影响范围较小,约为750 mm,不必考虑多车效应;车轮作用于横隔板上方顶板时,其纵向影响范围约为2个横隔板间距。
2)顶板-U肋连接焊缝焊根和焊趾处的疲劳损伤度D对车轮的横向作用位置e均较为敏感。荷载横向偏移e较小时,焊根处疲劳损伤较大;反之,焊趾疲劳损伤较大。文中模型偏移分界值e=450 mm。
3)相对未开设过焊孔,开设有过焊孔的模型在荷载同一横向作用位置下的焊缝局部应力有所降低,但疲劳损伤度大幅上升,且最不利荷载位置产生偏移。
4)根据笔者提出的轮迹分布方法计算所得疲劳损伤度,比《规范》的计算结果高10%以上,建议顶板-U肋连接焊缝处疲劳损伤度计算时将车轮横向影响范围扩大至750 mm。

