基于实测数据的沥青路面温度场年变化回归分析

梁乃兴，俞靖洋，于 伟，李 媛

(重庆交通大学 土木工程学院，重庆400074)

0 引 言

沥青路面长期暴露在自然环境中，这就要求沥青路面结构不仅要具有满足行车荷载要求的力学性能，还要具有抵抗环境因素破坏的耐候性能。环境因素对路面结构的影响主要表现在对路面温度场的影响，即：①沥青材料的模量随着温度场的变化而变化；②路面结构温度场的变化导致路面结构内产生温度应力。环境因素包括温度、太阳辐射、降水、风等，其中任何一个因素的改变都将影响路面结构的温度场[1]，而温度是造成沥青路面产生车辙甚至开裂病害的重要因素之一[2,3]。国内外学者针对温度对沥青路面温度场的影响做了大量研究，E. S. BARBER[4]首先推导出了路面最高温表达式，为沥青路面温度场研究提供了重要参考依据；康海贵等[5]根据实测的沥青路面温度，分别给出了升温阶段和降温阶段沥青路面温度的预估模型；甘新立等[6]建立了沥青路面低温温度场预估模型，对比了模型与国外现有模型之间的计算精度；延西利等[7]通过实测分析，分别给出了高温、低温以及常温时期沥青路面温度场变化规律；韩丁丁等[8]针对北京地区沥青路面温度场的实测数据，分析了路面结构内部温度梯度以及升、降温速率的变化规律；孙强等[9]分别建立了沥青面层温度和路面结构温度随深度的变化方程；邹晓翎等[10]以二阶段函数的形式建立了水泥、沥青路面温度场模型，该模型拟合精度较高，但模型采用分段函数来表示路面温度场的变化规律，相对较为复杂。以上研究多是针对某些特定条件下的路面温度场进行的，而对任意时刻路面温度场的研究相对较少。

2011年，笔者对云南大理地区气温以及沥青路面结构温度场进行了为期一年的实测，基于对实测数据回归分析的结果，结合当地气温及沥青路面日温度场变化规律，对双正弦函数模型[11]进行了分析，建立了修订双正弦函数模型(即气温模型)，并对比了修订前后的双正弦函数模型计算结果与气温实测值之间的相关性系数；基于该修订双正弦函数模型，建立了沥青路面晴天日温度场模型，并将温度场模型计算结果与实测数据进行了对比。结果表明，笔者提出的气温模型以及温度场模型均具有较高的计算精度，可以为后续沥青路面在非线性温度梯度作用下温度应力的计算以及沥青路面的设计提供参考。

1 温度数据采集

云南省位于我国西南地区，具有纬度低、海拔高、地形地貌复杂的特点。7月为气温最高月，该月日平均气温为19～22 ℃；1月为气温最低月，该月日平均气温为6～8 ℃。降雨主要集中在6—8月，此期间降水量可达年降水量的60%以上。

1.1 试验路段路面结构

选择云南大理关巍一级公路上一段四周无建筑物遮挡、通风良好且太阳辐射充足的沥青路面作为温度的采集点。试验路段路面结构见表1。

表1 试验路段沥青路面结构Table 1 Asphalt pavement structures in test section

1.2 实测数据采集

用PC-4型便携式自动气象站采集2010—2011年云南省试验路段全年大气温度，得到试验段气温实测数据。

按照钻心法埋设ZDR-41型智能温度记录仪，埋设深度z分别为1、2、4、6、8、10、18、30 cm，采集频率为1次/h，得到2010—2011年云南省试验段沥青路面温度场实测数据。

2 晴天日气温模型

2.1 气温模型函数

2.1.1 双正弦函数模型函数

严作人[11]考虑气温日变化规律为升温时间长而降温时间短的特点，根据导热方程及传热学基本理论，采用2个三角函数叠加的方式，建立了表征大气温度日变化规律的双正弦函数模型(1)：

0.146sin[2ω(t-τ0)]}

(1)

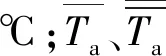
双正弦函数模型(1)较好地反应了气温的日变化规律，但由于没有考虑太阳辐射角年周期性变化对气温日变化规律的影响，故需进行修订。

2.1.2 修订双正弦函数模型函数

图1为笔者在云南大理地区实测的沥青路面结构冬季代表日(2011年1月21日)及夏季代表日(2011年6月18日)的气温变化曲线。

图1 云南大理地区2011年代表日实测气温日变化曲线Fig. 1 Daily variation curves of measured temperature of representative days in Dali, Yunnan, 2011

由图1可知，以三角函数表征气温变化规律时，代表日升温和降温起始时间的初相位随季节呈周期性变化。由于太阳直射角在南北回归线之间呈年周期性变化，造成冬季日出较晚、夏季日出较早，所以，初相位值夏季偏小、冬季偏大；同时，最高气温的高低在一定程度上就可以反应太阳辐射的大小。因此，笔者根据2011年云南大理地区实测气温数据，考虑不同月份对初相位的影响，对式(1)进行修正，得到修订的双正弦函数模型函数，如式(2)：

0.146sin[2ω(t-τ′0)]}

(2)

式中：τ′0为与月份值D(D取值见表2)相关的初相位，h；其他符号同前。

2.2 修订双正弦函数模型的回归分析

根据国家气象中心发布的气象资料筛选出2011年云南大理地区各月晴天日气温数据，将各月晴天日不同时刻气温取平均值，得到各月不同时刻的气温平均值。限于篇幅，图2仅列出了2011年夏季和冬季代表月(7月、1月)不同时刻的平均气温。

图2 云南大理地区2011年代表月不同时刻平均气温Fig. 2 Mean temperature at different moment of representative months in Dali, Yunnan, 2011

将2011年各月不同时刻气温平均值带入式(2)进行拟合，各月初相位τ′0及拟合相关系数R2计算结果见表2。表中D为月份值。

表2 初相位τ′0及拟合相关系数R2Table 2 Initial phase τ′0 and fitting correlated coefficient R2

由表2可见，各月拟合相关系数R2>0.92，拟合效果良好。表征升温起始时间初相位τ′0的拟合值夏季小而冬季大，这与夏季日出时间早而冬季日出时间晚的实际状况相符。

对表2中初相位τ′0拟合值和月份值D再次进行回归分析，发现τ′0与D较好地符合二次多项式分布(图3)，函数式如式(3)：

(3)

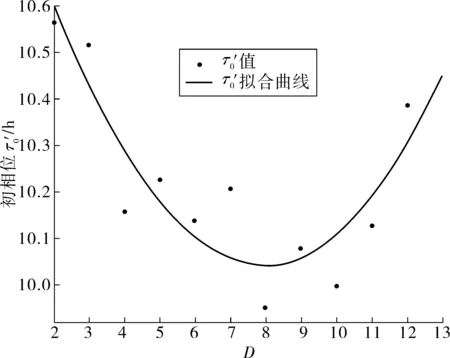
图3 τ′0拟合Fig. 3 τ′0 fitting

将式(3)带入式(2)，即得到修订双正弦函数模型，如式(4)：

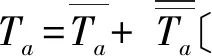
(4)

2.3 修订双正弦函数模型计算精度验证

分别采用修订前、后双正弦函数模型〔式(2)、式(4)〕计算云南大理地区2010、2011年晴天日气温计算值，再将计算结果与实测数据进行相关性分析，以相关系数R2反应模型的计算精度。计算结果见表3。

表3 气温模型相关系数R2Table 3 Correlated coefficient R2 of temperature model

由表3可知，

1)由于笔者提出的修订双正弦函数模型考虑了太阳辐射角的年周期变化对气温升温起始时间的影响，该模型能够更加精确地计算出不同月份晴天日气温值。

2)对比发现，修订双正弦函数模型计算精度更高，而且公式并不复杂。

3 路面温度场回归分析

3.1 实测沥青路面温度场分布规律

根据2011年云南大理地区沥青路面温度场实测数据以及大理地区气温实测数据，分别绘制出夏季和冬季代表日(6月19日、1月21日)各时刻实测的气温曲线和沥青路面不同深度z处温度日变化曲线，如图4。

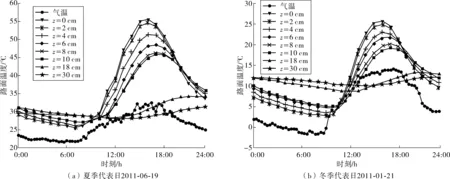
图4 云南大理地区2011年代表日各时刻气温及沥青路面不同深度z处温度日变化曲线Fig. 4 Temperature diurnal variation curves of different depths z of asphalt pavement and air temperature at different moment of representatiue days in Dali, Yunnan, 2011

由图4可看出沥青路面结构内温度场变化与气温变化的规律：①路面结构内不同深度z处温度变化与气温变化规律相似；②随着路面深度的增大，温度变化幅度减小，但均围绕着同一基准线呈周期性上下波动；③随着路面深度的增大，温度变化表现出一定的滞后性，随着温度逐渐向深层传递，滞后时间逐渐增加。

3.2 沥青路面晴天日温度场模型

3.2.1 沥青路面晴天日温度场模型函数

根据实测沥青路面温度场分布规律，考虑温度场变化与气温之间的关系，基于修订双正弦函数模型，建立沥青路面晴天日温度场模型函数(5)：

(0.015 9D2- 0.253 4D+ 11.05) +c]}〕

(5)

式中：T′a为一日内沥青路面任意深度处温度计算值，℃；a为温度参数，表示温度振幅随路面深度z增加逐渐减小；b为路面结构内平均温度与气温之差；c为时间参数，表示温度场随深度变化的滞后性；其他符号同前。

将云南大理地区2011年各月晴天日不同路面深度z处温度实测值取平均，记为各月不同路面深度处平均温度，带入温度场模型函数中进行拟合分析，可得到各月不同路面深度处参数a、b、c的拟合值，拟合结果见图5。参数拟合过程中，各月拟合相关性系数R2均在0.87以上，拟合效果良好。

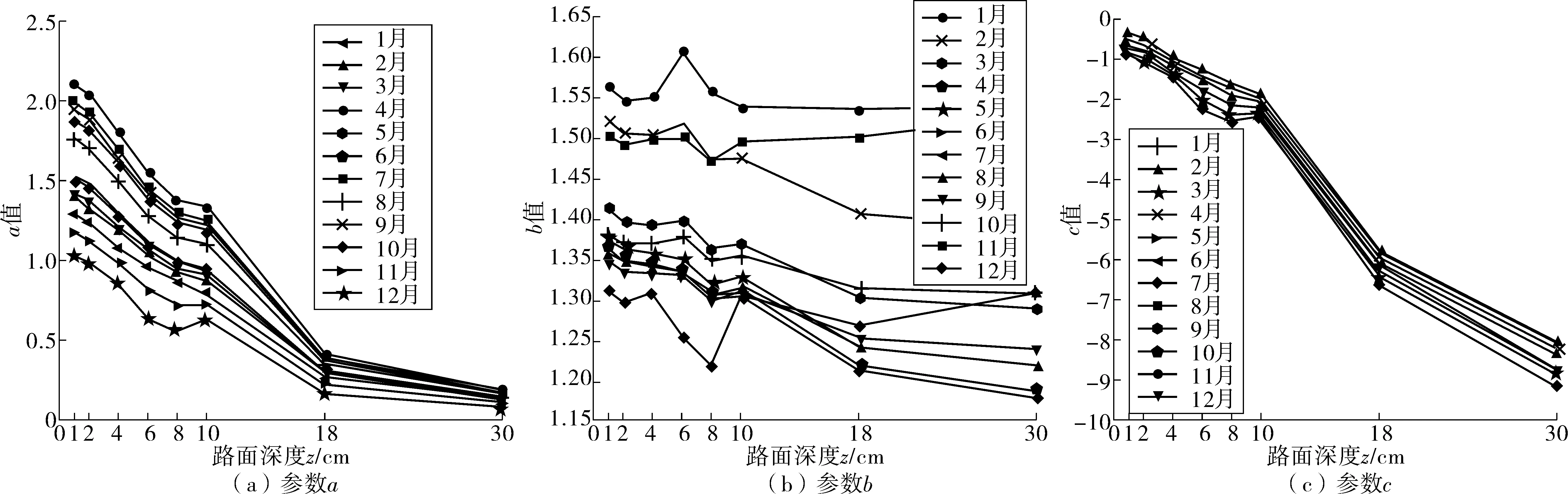
图5 参数a、b、c与沥青路面深度z的关系Fig. 5 Relationship between parameters a, b, c and depth z of asphalt pavement

3.2.2 参数a回归分析

由图5(a)可知，参数a值与沥青路面深度z符合二次多项式分布，将各月不同深度处参数a拟合值和深度z按式(6)进行拟合，拟合结果见表4，表中D′为计算当月的月份值。

a=p1z2-p2z+p3

(6)

式中：p1、p2、p3为拟合参数。

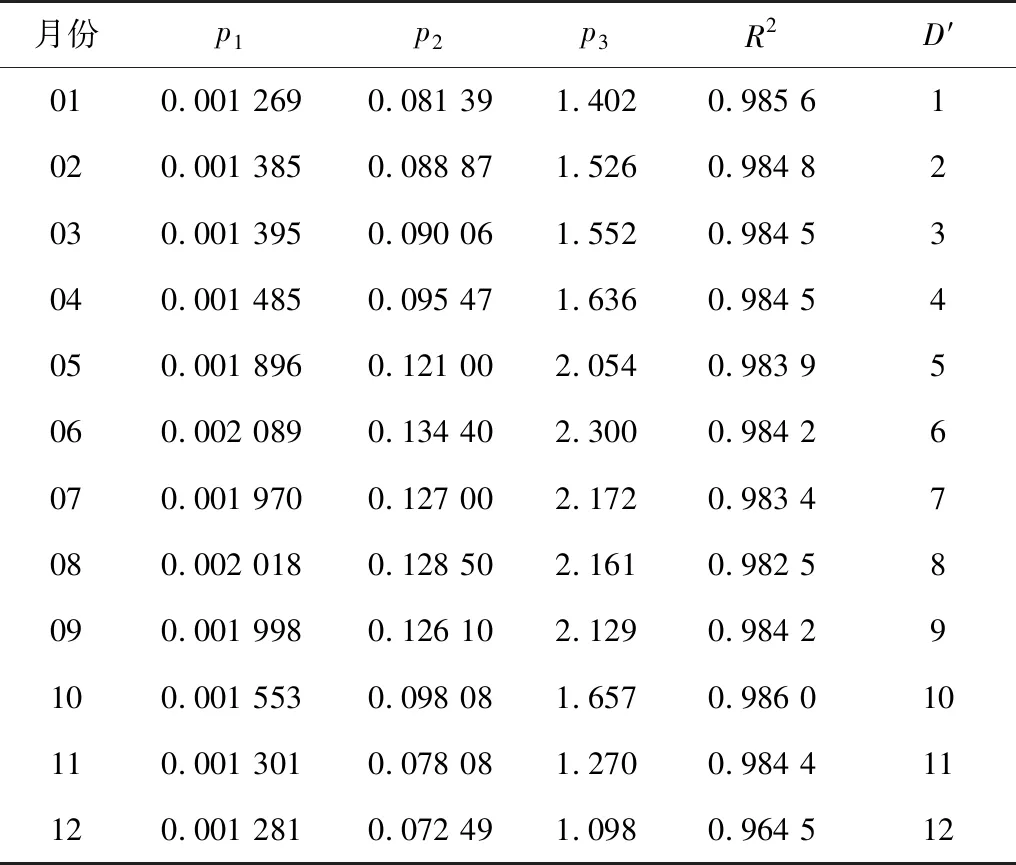
表4 参数a拟合Table 4 Parameter a fitting

由表4可知，p1、p2、p3分别满足式(7)～式(9)：

(7)

(8)

(9)

3.2.3 参数b回归分析

由图5(b)可知，参数b随着沥青路面深度z变化较小，但b值随着月份值改变而变化。分别求出各月参数b拟合值的平均值，该平均值与月份值D′ 能够较好地满足二次多项式(10)的关系：

(10)

3.2.4 参数c回归分析

由图5(c)可知，参数c随着沥青路面深度z呈线性变化，各月变化幅度相似，这一规律与实际相吻合。由于材料导热系数不变，故随着沥青路面深度的增加，温度变化滞后性相同。分别求出沥青路面不同深度处参数c拟合值的平均值，再以线性函数进行拟合，该平均值与路面深度z之间的表达式见式(11)：

(11)

3.2.5 沥青路面晴天日温度场模型建立

将式(7)～式(11)带入式(5)中，得到温度场模型拟合方程(12)：

(0.015 9D2- 0.253 4D+ 11.05) +c]} +

0.146 sin{2ω[t- (0.015 9D2- 0.253 4D+ 11.05) +c]}〕

(12)

用式(12)求出2011年云南大理地区沥青路面晴天日温度场模型计算值，与同年试验段沥青路面晴天日温度场实测数据进行对比，并计算预估值与实测数据之间的相关性系数R2。结果表明，R2均在0.81以上，说明实测值与模型计算值之间具有较高的相关性。限于篇幅，笔者只附上了2011年1月21日温度实测值与模型计算值的对比，如图6。

图6 2011年1月21日路面结构不同深度处温度变化曲线Fig. 6 Temperature variation curves of pavement structure at different depths on January 21, 2011

由图6可见，温度场模型(12)能够准确地计算出晴天日沥青路面结构内不同深度处的温度，证明沥青路面晴天日温度场模型具有较高的计算精度，能够准确地反应路面结构随时间、深度变化的三维分布。

笔者以相关性系数为控制指标，通过回归分析的方法建立了沥青路面晴天日温度场模型(12)，该模型具有以下优越性：

1)模型仅需要2个未知量——日平均气温、日气温振幅便可预估该日路面结构内部不同时刻温度场数值。

2)模型以月份值的方式表达太阳辐射角的年变化规律，仅需少量测量数据便可预测全年各晴天日路面结构温度场变化规律。

3)模型的整体计算精度高，但沥青路面温度场日最高、最低温预估值与实测值之间存在一定差异。

4 结 论

1)利用云南大理地区气温实测数据进行回归分析，考虑气温随太阳辐射角周期性变化规律，建立了修订双正弦函数模型；以相关性系数为检验标准进行计算精度检验发现，修订双正弦函数模型比修订前的双正弦函数模型具有更高的计算精度。

2)考虑沿路面结构深度方向温度变化的滞后性，以及太阳辐射角周期性变化规律，建立了沥青路面晴天日温度场模型。该模型简洁、便于运算，且预测精度较高，仅需测量每日的平均气温和日气温振幅便可计算出路面结构沿深度和时间的三维分布。通过模型计算值与实测值进行对比可以发现：沥青路面晴天日温度场模型能够反映晴天日沥青路面结构内部温度在不同时刻、不同深度的变化规律，从而可以为更加准确地计算沥青路面结构内温度应力和路面结构设计等工作提供依据。