突发状况下的道路网络故障演化分析
——以通州市区道路网络为例
万 蔚,黄雨晨,王振华,张 克,李梦琦
(1. 中国航天系统工程有限公司,北京 100070;2. 北京市计量检测科学研究院,北京 100029)
0 引 言
在道路交通网络中,车辆追尾、设施故障等突发事故导致交叉口或路段发生拥堵的事件时有发生,一些关键交叉口或路段的突发拥堵现象会随着时间的推移逐渐向相邻的路段或者节点传播,严重时可能会使得整个道路交通网络瘫痪。
国内外学者围绕道路交通网络故障的演化开展了广泛的研究。T. W. LAWSON等[1]采用图形化的方式来计算车辆拥挤和消散的时间,很好地区分了交叉口的延误和排队;P. G. MICHALOPOULOS等[2]为了描述交叉口拥挤的形成和消散情况,建立了推导延误的数学模型,给出了适用于单交叉口和联动交叉口的延误解析式;隽志才等[3]基于流体力学理论,构建了准冲击波模型,对交叉口处的拥挤-消散过程进行了模拟,较好地反映了信号交叉口处车流运行状态;吴建军[4]研究了不同性质的边(流量最大、介数最大、流量和介数组合最大)被移除后对道路网络的影响情况;俞斌等[5]基于交通波理论分析了事故发生在路段和交叉口两种不同情况下的影响范围模型;臧华等[6]采用车流波动理论探究了高速公路交通事故发生后,车辆排队长度的预测模型;卢顺达[7]研究了拥堵网络交通流量分配算法;张雄飞等[8]综合考虑拥挤交通网络的特点,建立了带转向延误和通行能力限制的交通网络配流模型;刘杰等[9]基于交通流理论合理确定道路的负载及容量,并将运输路段定义为正常和非正常2种状态,从道路和网络2个层次确定网络交通拥堵指数,通过仿真分析的方法对道路交通网络的级联失效程度进行宏观测度;张宏雨等[10]基于消圈算法,以拥挤网络中实时流量为研究对象,建立了以交通网络总阻抗最小为目标,以路段容量、饱和度、总流量守恒等为约束条件的模型,对拥挤网络流进行了深入研究;李成兵等[11]基于容量-负荷模型,分析了不同的攻击策略、容量系数、地理距离权重与节点度权重对城市交通网络级联失效的影响,研究网络可靠性的变化。以上学者主要利用排队论模型和交通波模型分析道路级联失效,计算量大且建模过程复杂,很难用于道路交通复杂网络系统的动态分析。
笔者基于耦合映像格子模型,综合考虑道路网络拓扑特性及流量特性的影响,提出了适用于道路网络的级联失效规律模型。首先,采用L空间法以交叉口为节点、道路为边,对通州市区城市道路网络进行抽象;然后,利用节点度K、节点介数Bi及节点强度Si等指标对通州市区城市道路交通复杂网络特性进行分析;最后,综合考虑道路网络拓扑特性及流量特性的影响,提出了基于CML的道路网络故障演化模型,仿真分析了不同扰动值、不同耦合强度组合下的道路网络级联失效的影响规律。研究结果可为突发状况下的道路网络管控措施提供技术参考。
1 数据基础
1.1 网络结构数据
1.1.1 研究范围界定
以通州市区为研究对象,研究范围西起温榆河西路、东至北京六环,北起潞苑北大街、南至玉带河东街(图1)。
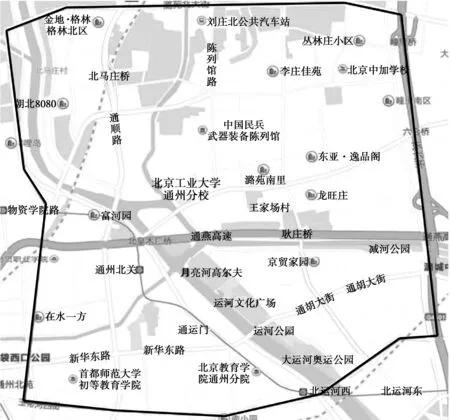
图1 通州市区道路网络研究范围Fig. 1 Research scope of urban road network in Tongzhou city
1.1.2 道路网络模型
道路交通网络中的要素多而复杂,在研究网络空间结构时,应剔除路段以外的因素,对道路网络进行抽象简化。笔者利用L空间方法将所研究交通网络的道路和交叉口简化为抽象网络中的点和边,从而节点i和j之间的邻接矩阵aij可按式(1)构建:
(1)
依据通州市区道路网络地图,构建通州市区道路交通网络拓扑图(图2)及其拓扑邻接矩阵(表1)。

表1 通州市区道路网络部分邻接矩阵Table 1 Partial adjacency matrix of urban road network in Tongzhou city

注:图中节点编号即道路交叉口序号。图2 通州市区道路交通网络拓扑图Fig. 2 Topological structure of urban road network in Tongzhou city
1.2 网络流量数据
在道路交通网络中,网络流量是影响运行状态的一个重要因素,若在高峰时间出现道路突发事件,极易造成道路交通堵塞,严重时甚至导致整个路网瘫痪。
1.2.1 道路网络OD车流分析
笔者采用人工观测法对通州市区主要道路交叉口进行交通量调查,调查时间为2017年6月11日—7月11日,早高峰07:30—09:30,晚高峰17:00—19:00。根据实际观测,整体路网的高峰时间在07:00—09:00,因此选取此段时间调查的交通流量作为高峰交通量。
将调查结果利用重力模型分4步进行推算:① 阻抗矩阵用出行时间表示,结合实际调查的关键路段流量和时间阻抗矩阵,推算出道路网络OD车流量;② 采用全有全无的交通分配法,把OD车流按照一定的规则分配到道路中的各条线路上,求得各个路段的断面车流量;③ 将分配的断面车流与关键路段实际调查的断面车流进行校核,不断调整,直至误差在允许范围内;④ 利用重力模型,得到路段断面车流量结果,如表2。

表2 通州市区道路网络部分路段断面车流量Table 2 Sectional flow of part of road network in Tongzhou city
1.2.2 道路网络度量指标
利用网络拓扑邻接矩阵a和流量分布矩阵w来分析节点度K、节点介数B以及节点强度S等参数。节点度K为与某节点直接连接的边数,节点介数Bi为网络中通过某节点i的最短路径数目除以所有最短路径的数目,按式(2)计算,节点强度Si为与节点i相邻边的流量总和,按式(3)计算:
(2)
(3)
式中:n为节点数目;σst为从节点s到节点t的所有最短路径的数目;σst(i)为从节点s到节点t经过节点i的所有最短路径的数目;wij、aij分别为节点i和j之间的流量矩阵和邻接矩阵。
2 道路网络故障演化模型
2.1 道路网络故障演化模型构建
为了研究道路交通网络故障态势演化规律,采用耦合映像格子来构建道路网络故障演化模型,如式(4):
i=1,2,…,N
(4)
式中:xi(t)、xj(t)分别为节点i、j在t时刻的状态;ki为节点i的度;c为耦合系数;f(x)为Logistix映射函数,f(x)=dx(1-x),当0≤x≤1时,0≤f(x)≤1。
式(4)为描述封闭系统中复杂时空动力学特征的一个模型,它将时间和空间离散化,但状态变量仍然保持连续。
2.2 道路网络故障演化模型改进
由于道路网络中拓扑结构和流量的变化都会导致网络故障的发生,为此,笔者在道路网络故障演化模型(4)中引入无权拓扑网络耦合系数ζ1及加权流量分布耦合系数ζ2,以研究道路网络故障演化规律,改进后的耦合映像格子模型如式(5):
ζ1、ζ2∈(0,1),ζ1+ζ2<1
(5)
在t时刻,道路上突然发生车辆追尾、设施故障等事故时,交叉口或路段易发生拥堵,即抽象网络中,在t时刻,对某一节点或路段施加一个外部扰动值R≥ 1,如式(6):

(6)

3 实例分析
3.1 道路网络特征分析
3.1.1 道路网络节点度分布
按照对特征参数的描述,通州市区道路网络的节点度分布如表3。

表3 通州市区道路网络节点度分布Table 3 Distribution of node degree of road network in Tongzhou city
3.1.2 道路网络节点度累积概率分布
为获得节点度与累积概率的分布形式,将通州市区道路网中的节点度与度累积概率的数据进行拟合,如图3。

图3 通州市区道路网络节点度K与累积概率PkFig. 3 Node degree K and cumulative probability Pk at urban road network in Tongzhou city
由图3可见,拟合系数R2=0.879 9,道路网络节点度与累计概率分布函数为Pk=1.136 1K-0.81,符合幂律分布,说明通州市区道路网络具有无标度网络特征,存在异质性关键节点。
3.1.3 基于节点强度和介数的节点排序
由于节点强度S反映网络流量分布状况,节点介数B反映网络结构,因此,笔者选取节点强度和节点介数来评价网络的关键节点。由表4可知,通州市区道路网络中,交叉口3是强度最大的节点,交叉口19是介数最大的节点。
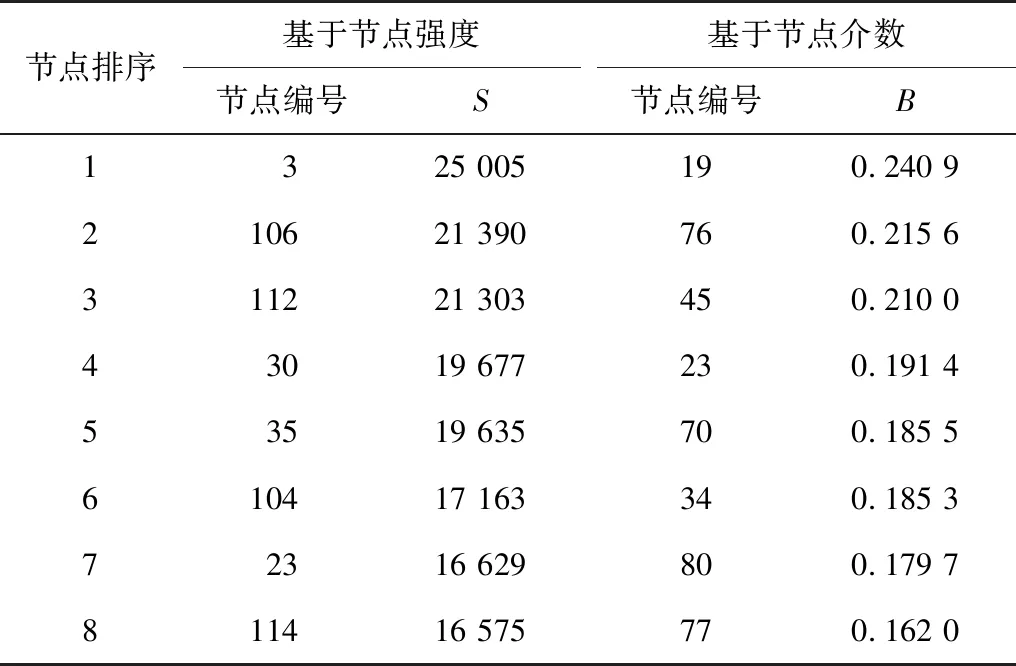
表4 基于节点强度S和节点介数B的节点排序Table 4 Node ranking based on node strength S and betweenness B
注:节点编号即为道路交叉口序号。
3.2 道路网络故障演化分析
在进行道路网络故障演化分析时,分别选取节点介数B最大(交叉口19)、节点强度S最大(交叉口3)的节点进行单个节点的蓄意攻击。
3.2.1 相继故障的阈值
根据研究范围内的道路网络邻接矩阵数据和道路网络断面流量数据,有ζ1=ζ2=0.25,进行道路网络故障演化的仿真,以分析蓄意攻击介数B最大(交叉口19)、蓄意攻击强度S最大(交叉口3)的节点时道路交通网络产生级联失效的阈值,并探讨道路网络故障演化规律。仿真结果如图4。

图4 道路网络故障扩散过程随外部挠动值R变化曲线Fig. 4 Curves of failure diffusion process of road network changing with external disturbance R
由图4可见,外部扰动值R越大,网络越容易发生级联失效,蓄意攻击介数最大的节点相继故障发生的阈值为1.6,小于蓄意攻击强度最大节点相继故障阈值1.8,说明蓄意攻击时拓扑网络比流量分布网络更不稳定。
相继故障发生比例与发生时间步呈正态分布如图5。在蓄意攻击介数最大的节点(节点编号为19)处,相继故障发生的高峰规模时间为第12时间步,早于蓄意攻击强度最大的节点3(相继故障发生的高峰规模时间为第17时间步)。这与通州市道路网络为无标度网络的性质相符合,说明介数大的节点在网络中起关键作用,施加在网络关键节点的扰动将导致故障快速传播。

图5 道路网络故障规模与时间步随外部挠动值R变化曲线Fig. 5 Curves of failure scale and time step of road network changing with external disturbance R
3.2.2 无权拓扑网络耦合系数ζ1的影响
在现有道路网络中,网络故障阈值为1.8,设外部扰动值R=2,加权流量分布耦合系数ζ2=0.25,无权拓扑网络耦合系数ζ1= 0.15、0.25、0.35、0.45、0.55、0.65,进行道路网络故障演化的仿真,分析ζ1对道路交通网络级联失效产生的影响,以探讨不同网络结构下的道路故障演化规律。从图6的仿真结果可以看出,当ζ2不变时,无论ζ1如何变化,道路网络均会发生级联失效,网络发生相继故障的时间和扩散速度几乎在同一直线上。
从相继故障发生的规模与时间步关系(图7)也能看出,无论是攻击介数最大的节点还是攻击强度最大的节点,不管ζ1如何变化,相继故障的扩散过程都出现同步现象。在蓄意攻击介数最大的节点时,相继故障发生的高峰规模时间为第12时间步,故障高峰规模为0.125~0.165;在蓄意攻击强度最大的节点时,相继故障发生的高峰规模时间为第16~第18时间步,故障高峰规模为0.105~0.140。与蓄意攻击流量最大的节点处相比,蓄意攻击介数最大的节点处,故障高峰出现的时间早,且规模大,进一步说明拓扑网络是不稳定的。

图6 道路网络故障扩散过程随 ζ1变化的关系曲线Fig. 6 Curves of failure diffusion process of road network changing with ζ1

图7 道路网络故障规模与时间步随 ζ1变化的关系曲线Fig. 7 Curves of failure scale and time step of road network changing with ζ1
3.2.3 加权流量分布耦合系数ζ2的影响
假设外部扰动值R=2,无权拓扑网络耦合系数ζ1=0.25,加权流量分布耦合系数ζ2=0.15、0.25、0.35、0.45、0.55、0.65,进行道路网络故障演化的仿真分析,结果如图8。由图8可见,在蓄意攻击强度最大的节点处,若ζ2<0.25,道路网络未发生级联失效;若ζ2>0.25,道路网络发生级联失效。在攻击介数最大的节点处,无论ζ2如何变化,道路网络均会发生级联失效,并且ζ2越大,网络越容易发生级联失效。

图8 道路网络故障扩散过程随 ζ2变化的关系曲线Fig. 8 Curves of failure diffusion process of road network changing with ζ2
从相继故障发生规模与时间步的关系(图9)来看,当ζ2>0.25时,在蓄意攻击介数最大的节点处,发生故障的高峰规模时间为第11时间步,故障高峰规模为0.130~0.140;在蓄意攻击强度最大的节点处,相继故障高峰规模发生的时间为第18~19时间步,相继故障高峰规模为0.105~0.125。因此,相关运营管理部门可以依据故障高峰时间步有效地控制级联失效的发生。

图9 道路网络故障规模与时间步随 ζ2变化的关系曲线Fig. 9 Curves of failure scale and time step of road network changing with ζ2
4 结 论
以通州市区城市道路网络为例,综合考虑道路网络拓扑特性及流量特性的影响,提出了基于CML的级联失效规律模型,仿真分析了不同扰动值、不同耦合强度组合下的道路网络级联失效的影响规律,得到以下结论:
1)对道路网络施加的外部扰动值R越大,网络越容易发生级联失效;道路网络发生级联失效的阈值为1.8;蓄意攻击介数最大节点的相继故障阈值为1.6,小于蓄意攻击强度最大节点的相继故障阈值为1.8,说明流量分布网络比拓扑网络稳定,要重点保护介数大的站点。
2)当加权流量分布耦合系数ζ2不变时,无论无权拓扑网络耦合系数ζ1如何变化,道路网络均会发生级联失效,网络发生相继故障的时间和扩散速度呈现一致性。
3)当无权拓扑网络耦合系数ζ1不变时,随着加权流量分布耦合系数ζ2的增大,网络越容易发生级联失效。建议相关运营管理部门依据故障高峰时间步来有效控制级联失效的发生。
—— “T”级联

