对平面几何问题求解入手点的思考

湖南省双峰县永丰中学 匡牡丹

在初中数学平面几何问题的求解中，我们会遇到各种类型题，每类题都有不同的思路和解法.这些题型是否具有共同的本质？不同的解法之间是否有相通之处？到底应该从哪里下手来解决这些问题？该如何作辅助线？下面，介绍一下笔者对于解答平面几何问题的思考与感悟.

一、从特殊角入手

在平面几何题目的条件中，往往给出一些特殊角，如30°、45°、60°（或150°、120°、135°）、90°等，或者两个角之间存在倍半关系，几个角之间存在和差关系.如果出现90°角，可以构造直角三角形，运用勾股定理求解；如果出现60°角，可以与其他条件相结合，构造等边三角形等.

在这类问题的求解中，利用这些特殊角，通过添加辅助线，构造特殊三角形，常常可以快速找到简洁的求解思路.

例1如图1所示，在△ABC中，点D在边AB上，且∠ACD=30°，∠BCD=90°.则

分析：本题中给了两个特殊角∠ACD=30°，∠BCD=90°，因此可基于此构造特殊三角形求解.

图1

图2

方法1：如图2所示，过点A作CD的垂线，交CD的延长线于点E.

在直角△ACE中，因为∠ACD=30°，所以AC=2AE.

在△ADE和△BCD中，∠AED=∠BCD=90°，∠ADE=∠BDC，所以所以，所以BC=3AE.

方法2：如图3，过点D作DF垂直AC于点F.

图3

二、从特殊边入手

特殊边或边的关系主要有：勾股关系，即一个三角形两边的平方和等于第三边的平方，进而可以得到直角三角形，利用直角三角形的有关性质，证明垂直关系.

边的倍、半、和、差关系等.与倍半有关的定理有：“直角三角形中，30°角所对的直角边等于斜边的一半”“直角三角形中斜边上的中线等于斜边的一半”“三角形的中位线等于相应边的一半”.

边的相等关系.主要有：“等角对等边”“平行四边形的对边相等”“轴对称图形的对应边相等”等.此外，还可以运用全等三角形得到边的相等关系.

解题中遇到与上述条件有关的问题时，首先应该想到应用这些关系，构造特殊图形.例如，当我们看到角平分线时，应想到过角平分线上的已知点作垂直于角的两边的线段；当我们看到中点时，应想到添加辅助线，使两中点所连线段成为某三角形的中位线.这样，许多难题便迎刃而解.

例2已知：如图4所示，在△ABC中，点M为AC边的中点，点E为AB上一点，且AB=4AE，连接EM并延长交BC的延长线于点D.求证：BC=2CD.

分析：本题的条件中含有相等线段及比例线段，因此可通过构造平行线或三角形的中位线等进行求解.

方法1：如图5，过点C作CF∥AB交DE于点F.

因为点M为AC的中点，所以AM=CM.

因为CF∥AB，所以∠BAC=∠MCF.又∠AME=∠CMF，AM=CM，所以，所以AE=CF.

因为AB=4AE，BE=AB-AE，所以BE=3AE，所以

因为BC=BD-CD，所以BC=2CD.

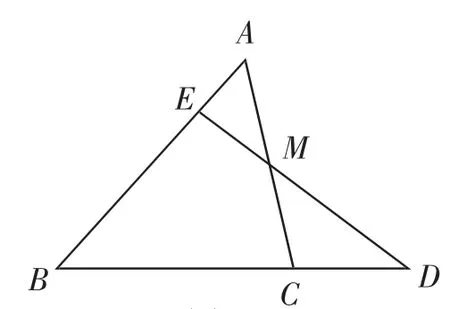
图4

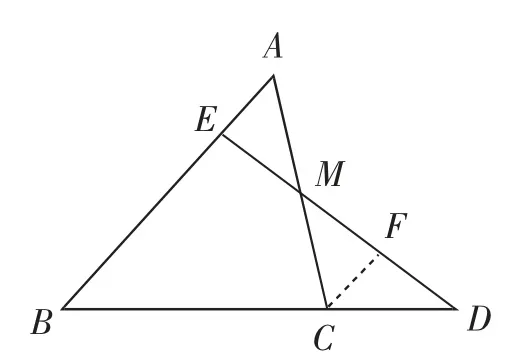
图5

方法2：如图6，过点C作CF∥DE交AB于点F.

图6

因为点M为AC的中点，所以AC=2AM，AF=2AE，AE=EF.

三、从特殊图形入手

特殊的图形主要包括正方形、长方形、等腰或等边三角形、平行四边形、菱形、圆等.例如，遇到涉及圆的问题，首先要想到构造已知直径所对的圆周角；若已知切线，要想到连接圆心和切点等.熟练运用辅助线，化未知为已知，从而解决不能直接运用定理解决的平面几何题.

例3如图7所示，点C是以AB为直径的圆O上一点，直线AC与过点B的切线相交于点D，点E是BD的中点，直线CE交直线AB于点F.

（1）求证：CF是圆O的切线；

（2）若ED=3，EF=5，求圆O的半径.

分析：本题所给的条件中有直径、有切线，据此构造垂直关系，可迅速找到解题的切入点.

（1）方法1：如图8，连接CB、OC.

因为BD为圆O的切线，AB是圆O的直径，所以∠ACB=90°，∠ABD=90°，∠BCD=90°.

因为∠BCD=90°，点E是BD的中点，所以CE=BE，所以∠BCE=∠CBE.又因为∠OCB=∠OBC，所以∠OBC+∠CBE=∠OCB+∠BCE=90°，所以OC⊥CF.

所以CF是圆O的切线.

图7

图8

方法2：如图9所示，连接OE.

因为DB是圆O的切线，所以∠OBD=90°.

因为AB为圆O的直径，所以BC ⊥AD，所以△BCD是直角三角形.

图9

因为∠BCO=90°，点E为BD的中点，所以CE=BE.

在△OCE和△OBE中，OC=OB，OE为两三角形的公共边，CE=BE，所以所以∠OBE=∠OCD=90°，所以OC⊥CF.

所以CF是圆O的切线.

（2）解：因为CE=BE=DE=3，EF=5，所以CF=CE+EF=8.

因为∠ABD=90°，所以∠EBF=90°.又因为∠OCF=90°，所以∠EBF=∠OCF.又因为∠F=∠F，所以所以，所以OC=6，即圆O的半径为6.

另外，需要注意的是，在某一问题中这些关系并不是独立给出的，求解时要综合运用这些特殊关系.

总之，在平面几何问题的求解中，熟练运用特殊角、特殊边、特殊图形，快速联想，熟记定理，适当添加辅助线，运用这些方法，即可快速找到问题的求解思路，从而顺利、准确解决问题.