注重课堂实践，提升学科素养——由课堂裁剪与折纸经营几何学习

山东省广饶县实验中学 任百义

数学的几何学问可谓“小题大做”，初中生的思维常常有“短路”现象，这主要是因为教师在培养学生的“数形转换”的学科素养上缺乏实践.怎样才能让学生在课堂上多实践呢？通过备课组的集体研讨和平时的教学实践分析，裁剪与折纸是课堂上培养学生的“数形转换”学科素养的有效途径.

与课堂实践不谋而合，近年来中考试卷中考查裁剪与折纸的问题屡见不鲜.如2017年江苏省无锡市数学试卷第10题：如图1，△ABC中，∠BAC=90°，AB=3，AC=4，点D是BC的中点，将△ABD沿AD 翻折得到△AED，连接CE，则线段CE的长等于（ ）.

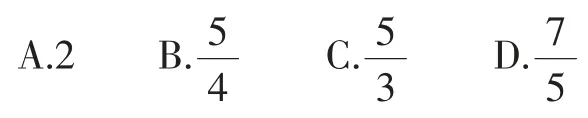
图1

中考试题是数学学科核心素养考查的具体体现，而课堂教学是培养学生学科素养的有效途径.为此，笔者在初中几何教学过程中开始尝试裁剪与折纸的数学拓展性课程，让学生初步体验到剪裁与折纸在数学学习中的一些“学问”.

一、课堂裁剪与折纸可以丰富数学探索的内涵

数学几何最显著的特点是“数形转换”的思想.在实验操作中让学生体验这种思想发现的过程，感悟数学的内涵是课堂教学的基本点.比如，在学习“勾股定理”内容时，教材就给出了剪纸证明的方法，剪裁四个相同的直角三角形进行拼接，然而学生拼接的方法是丰富多彩的，与教材有着不同的形式.在学习“等腰三角形”时，不妨在课堂上让学生思考将一张长方形纸片折成等腰三角形；再学习用直角三角形及任意三角形纸片折成一个长方形.当然，折纸必须强调重叠部分只能是两层纸，不能反复重叠.通过课堂上剪裁与折纸活动和小组交流酝酿出很多不同的方法，然后通过学生对折纸过程和相应的说明展示，让课堂变得活泼且有趣，学生对知识的探究由情而发.

毋庸置疑，笔者在课堂上采用的这些鲜活的案例都取得了很好的效果，有时，剪裁与对折活动从课堂中延伸到了课堂外，充分说明调动了学生学习数学的热情.在适当的时候展示与剪裁、折纸的内容有关的中考试题，使学生对剪裁、折纸的学习重视起来.

二、课堂裁剪与折纸数学探索案例分享

剪裁与折纸可以作为一种生活欣赏的艺术，用于几何教学则是作为有着除艺术欣赏之外的教学辅助工具的功能，其教学应用价值和使用手段尚有待师生认知、认可.同时，剪裁与折纸还面临着各种挑战，其应用和教学活动只是在摸索和尝试的过程中.笔者就以平行四边形的教学过程为例，将课堂裁剪与折纸数学探索与同人分享.

1.创设剪裁与折纸情境，引入新课

师：同学们，我们在前面学习过了三角形的知识，在那里我们认识了一些特殊三角形，如等腰三角形、直角三角形等，同时学习过一般四边形的性质，从今天开始，让我们再研讨一类特殊的四边形，好吗？（拿出一张16开纸板，将宽对折并剪裁）

师：在小学就知道这是一个什么四边形？

学生答长方形或矩形.

用电子白板展示折纸过程，如图2所示.

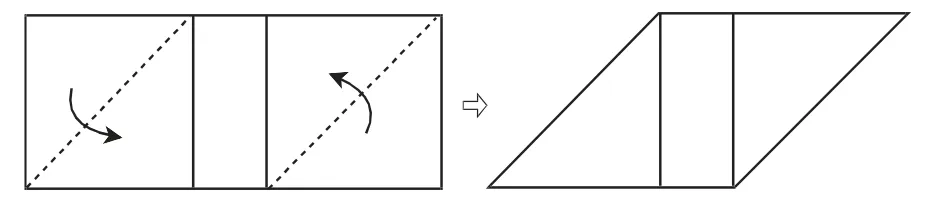
图2

学生在电子白板的示范下开始剪裁和折纸.

师：你们通过折纸得到了一个什么四边形？

生：平行四边形.

师：开始的16开纸也是平行四边形吗？

生：也是，只不过有些特殊.

师：这节课我们就开始学习平行四边形.我们在前面探究过许多图形，可以从哪些方面开始探究一个图形的特征呢？

生：需要探究平行四边形的定义、性质，还有判定等.

师生合作认识平行四边形的定义、表示符号.

2.通过剪裁与折纸探究平行四边形的性质

师：同学们，现在我们已经掌握了平行四边形的定义、表示符号（拿起学生刚刚折出的平行四边形），大家觉得可以从哪些角度去探究这个平行四边形的性质呢？

学生答边、角、对角线等.

由学生自己通过猜想和度量来证实猜想：平行四边形的对边相等、对角相等.

电子白板展示平行四边形的性质.

师：你们能够证明上面两个猜想吗？请先将这段文字写成数学命题的形式，然后证明.

学生作图、写出已知和求证，以及证明过程.

如图3，在四边形ABCD中，AB∥CD，AD∥BC.

求证：AB=CD，AD=BC，∠A=∠C，∠B=∠D.（证明过程略去）

课堂练习：（用电子白板展示课堂练习，巩固所学知识）

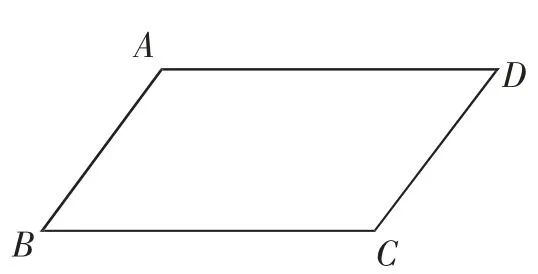
图3

在图3中，若∠A=120°，则其他几个角的度数分别是多少？

若AB=2，BC=4，∠A和∠B的度数分别是多少？

创设目的：采取先同桌交流再全班展示的方式进行.目的是训练学生对平行四边形对边相等、对角相等的性质的理解.

3.课堂上类比折纸，度量平行四边形的高的概念

师：（拿出一个已经折好的平行四边形）现在让我们回过头再看看这个图形的折纸过程（展开），请同学们思考这样一个问题.

电子白板展示：

课堂练习：如图4，四边形ABCD是平行四边形，作DE⊥AB，BF⊥CD，垂足分别为点E、F.求证DE=BF.

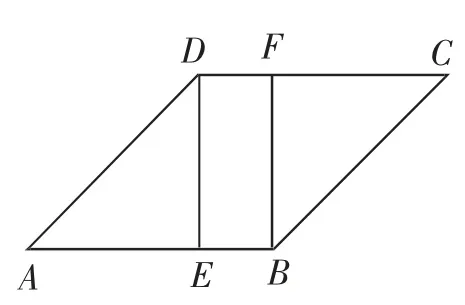
图4

答案是开放的、不唯一的，因此，学生交流后的答案精彩纷呈.预设学生可能的思路有以下几种：

思路1：利用▱ABCD对角相等、对边相等的性质可以得出∠A=∠C、AD=CB，再利用不难得出DE=BF.

思路2：得出DE=BF，或四边形DEBF的四个角为90°，证明四边形DEBF也是平行四边形.

思路3：引导学生从平行线间的距离进行探究证明.

创设目的：通过学生在课堂上对问题的讨论与交流，让应用折纸作为辅助探究的工具和演示几何形态成为可能，为学生针对几何问题敞开探究、开放的大门.因此，多角度的思考可以博采众长，有效提升学生对几何图形的认知能力.

4.创设剪裁与折纸练习题，让学生明确数学学科核心素养

为了开发剪裁与折纸活动，笔者用坐标纸作为数学教学专用折纸纸张，不但有网格可以表示坐标，还可以用不同的颜色表示剪裁或折叠后的区域等，从而让学生能直观地应用剪裁或折纸.比如，让学生练习一些必要的习题，可从中考试题中选编过来.如：

练习1：如图5，把一张长方形纸片对折，折痕为AB，再以AB的中点O为顶点把平角∠AOB三等分，沿平角的三等分线折叠，从折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是（ ）.

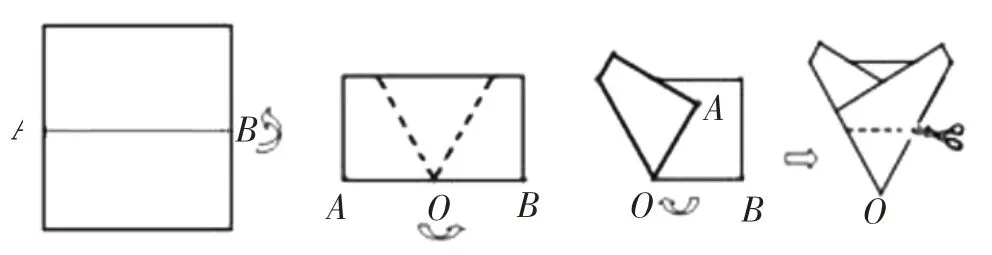
图5

A.正三角形 B.正方形

C.正五边形 D.正六边形

练习2：如图6，方格纸中有一透明等腰三角形纸片，按图中裁剪线将这个纸片裁剪成三部分.请你将这三部分小纸片重新分别拼接成：

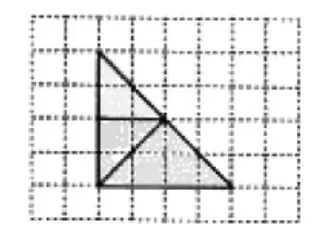
图6

图7

（1）一个非矩形的平行四边形.

（2）一个正方形.

请在图中画出拼接后的图形，要求每张三角形纸片的顶点与小方格的顶点重合……

创设目的：通过练习来营造一种动手实验、直觉判断、合情推理的数学认知过程，在活动中，学生根据自己的能力得出不同层次的结论.练习中的剪裁与折纸过程足以激励每一个学生参与到力所能及的探究中.

总之，在课堂上创设相应的剪裁与折纸活动，能为学生仔细观察，广泛联想，多方向、多角度、多层次去思考营造机会，因此，剪裁与折纸是发展学生数学学科核心素养的有效途径.