倾斜轴颈滑动轴承混合热弹流研究

王家序，倪小康，韩彦峰，向果，肖科

(1.重庆大学机械工程学院，重庆，400044；2.机械传动国家重点实验室(重庆大学)，重庆，400044)

在重载工况下，轴颈受载倾斜对滑动轴承的混合润滑特性会产生不可忽略的影响，造成轴承润滑状态恶化以及机械零部件失效。国内外学者在倾斜轴颈滑动轴承润滑特性方面进行了大量研究，如：XU 等[1]研究了在考虑湍流以及热效应的影响下，不对中滑动轴承润滑静态以及动态特性；张振山等[2-3]建立了考虑轴颈偏斜的滑动轴承TEHD模型，深入研究了热(弹性)变形对滑动轴承流体动力润滑性能的影响；孙丽军等[4]研究了考虑轴颈倾斜的重载轴承性能，并通过现场试验验证了理论的正确性；HE等[5-7]建立了船舶艉轴的混合润滑模型，分析了润滑表面形貌、微凸体接触力和轴承下沉量等因素对艉轴承润滑性能以及动态特性影响；陆金铭等[8]建立了船舶艉轴和中间轴轴承的润滑模型，研究了推进轴系轴颈倾斜对滑动轴承润滑性能的影响；HE 等[9]基于简化轴系法，分析了非对称偏转引起的结构参数和角度对滑动轴承压力分布、油泄漏、速度场和温度场的影响；邓玫等[10]对轴受载变形导致轴颈在轴承中倾斜时滑动轴承的热弹性流体动力润滑特性进行研究；SUN等[11-13]分析了轴颈受载偏斜对于滑动轴承流体动力润滑性能的影响，并开展了试验研究。以上研究主要从滑动轴承等温混合润滑特性和热弹流特性2个方面进行，没有深入考虑轴-润滑介质-轴承-环境之间热传导效应的影响，为此有必要对热效应下的滑动轴承混合润滑行为进行研究。本文建立更贴近工程实际的滑动轴承混合热弹流(mixed-TEHD)模型，综合考虑轴-润滑介质-轴承-环境之间的热传导效应以及润滑剂黏性耗散和微凸体接触热的影响。热求解模型将轴、润滑剂和轴承视为一个耦合热传导体(以下简称为JLB)，通过数值模拟对比研究了轴颈受载倾斜及对中状态下润滑界面的粗糙接触压力、摩擦因数、热变形分布以及JLB温度场，综合分析轴颈受载倾斜对滑动轴承混合热弹流润滑特性的影响。

1 数学模型与控制方程

倾斜滑动轴承简图及坐标系如图1所示，其中，θ为圆周角，ω为轴颈角速度，W为总荷载，ψ为偏位角，γ为倾斜角，e为偏心距。

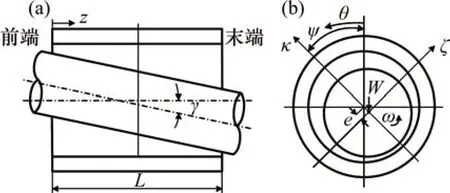
图1 倾斜滑动轴承简图及坐标系Fig.1 Geometry and coordinate system of misaligned journal bearing

1.1 平均雷诺方程

在重载工况下，轴承处于混合润滑状态，此时粗糙峰接触行为对润滑性能的影响不可忽略。本文采用稳态平均雷诺方程求解接触界面的油膜压力[14]：

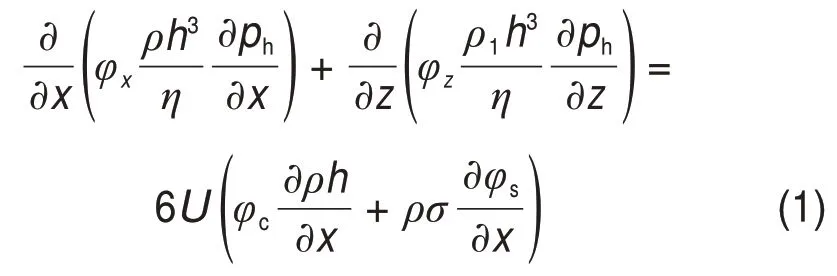
式中：ph为油膜压力；φx和φz分别为x和z方向的流动因子；φc和φs分别为接触因子和剪切因子；ρ1为润滑剂密度；σ为表面粗糙度的均方根；η为润滑剂黏度；h为膜厚；U为转动方向的表面线速度。

1.2 热传导模型

模型中将轴-润滑介质-轴承视为一个耦合热传导体，即JLB。采用欧拉方法将油膜的热对流方程以及轴与轴承的热传导方程统一为极坐标下热平衡方程，避免了求解轴-润滑介质以及轴承-润滑介质界面存在的复杂边界问题[15]。单位体积rΔθΔrΔz下热平衡方程为

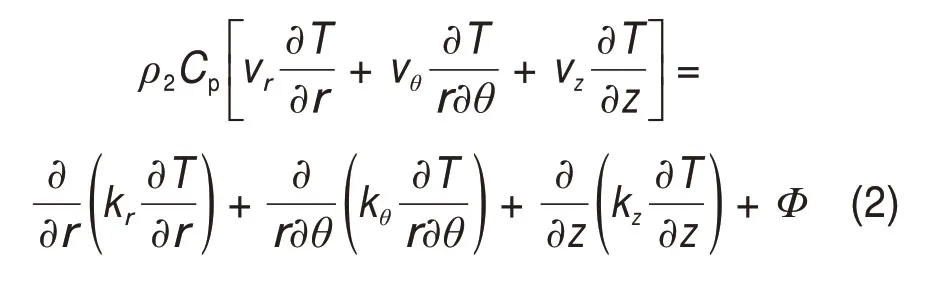
式中：ρ2为流体或固体材料密度；Cp为流体或固体材料比热容；kr，kθ和kz分别为r，θ和z方向上导热系数；vr，vθ和vz分别为r，θ和z方向上速度分量；T为温度；Φ为热源，由润滑剂粘性耗散ΦV和微凸体接触热ΦC2 个部分组成，其数值计算方法为

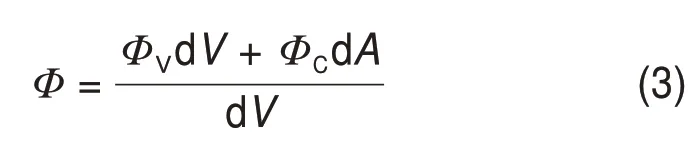
式中：dV是油膜单元体积；dA是与之相对应轴与轴瓦的接触面积。

本文热分析中网格划分如图2所示，采用的热传递边界条件[15-16]如图3所示。

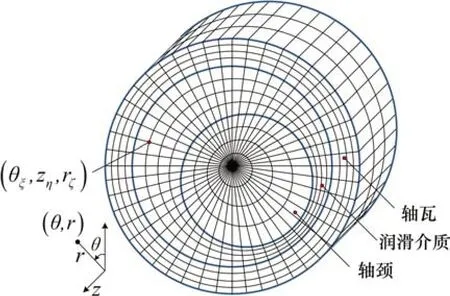
图2 热分析网格划分示意图Fig.2 Schematic representation of meshing under thermal analysis

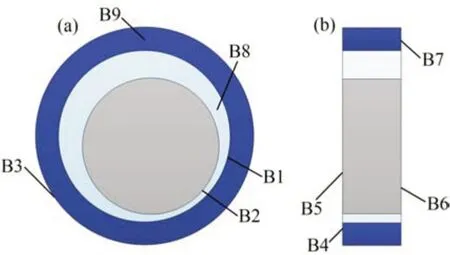
图3 滑动轴承热边界条件示意图Fig.3 Thermal boundary conditions of journal bearings

1)内边界条件：B1 和B2 分别为轴承-润滑介质以及润滑介质-轴界面间的等温边界条件；

2) 外边界条件：B3～B7 为热场外边界条件，其中，供油温度T=T0；绝热边界对流边界式中：T0和T∞分别为入口温度和环境温度和，hh为对流换热系数。

3)空穴边界条件：B8 为空穴边界条件，采用KNIGHT等[17]提出的气泡模型。

4) 进油口边界条件：B9 为进油口边界条件，由于热润滑剂的再循环，其温度需要根据供油温度进行调整，表示为

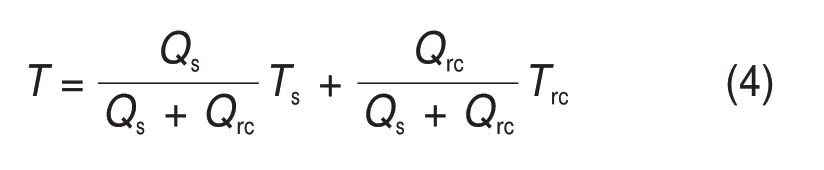
式中：Qs和Qrc分别为进油与循环油的流量；Ts和Trc分别为进油和循环油的温度。

1.3 膜厚方程

油膜厚度由几何间隙h0，轴与轴承的固体变形量δJ(θ,ΔT,p)和δB(θ,z,ΔT,p)这3 个部分组成，其计算公式为

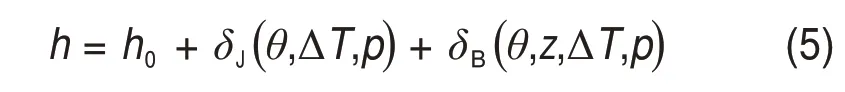
式中：h0=c(1 +εcos(θ-ψ))+ tanγ(z-L/2)；c为半径间隙；ε为偏心率；z为轴承轴心线方向长度；L为轴承宽度；p为油膜压力与接触压力之和。轴-轴承摩擦副示意图如图4所示，轴受载倾斜在轴承中的倾斜角γ参考文献[18]由公式γ=(WL2)/(16EI)计算(其中，W为外载荷，E为轴弹性模量，I为轴截面惯性矩)。

图4 轴-轴承摩擦副示意图Fig.4 Friction pair of shaft and journal bearings

轴与轴承的固体变形包括径向弹性变形以及热变形，本文所采用轴(45钢)的弹性模量大于滑动轴承瓦块(巴氏合金)的弹性模量，因此，只考虑轴承表面的弹性变形，并采用影响系数法求解[19]，如下式所示：

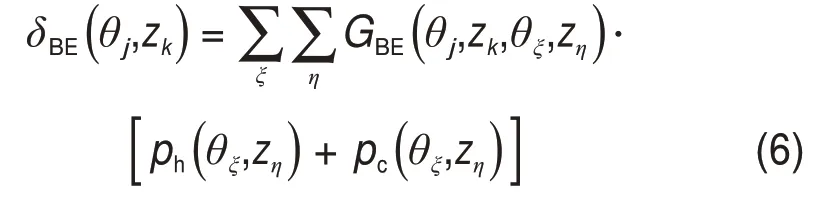
式中：δBE(θj,zk)为轴承在节点(θj,zk)处的弹性变形；GBE(θj,zk,θξ,zη)为滑动轴承轴瓦弹性变形影响系数；ph(θξ,zη)和pc(θξ,zη)分别为节点(θξ,zη)处的流体压力和接触压力。

本文假定旋转轴温度均匀，其热变形通过线膨胀公式计算：

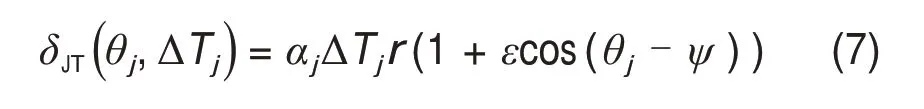
式中：δjT(θj,ΔTj)为轴颈热膨胀；αj为轴线膨胀系数；ΔTj为轴平均温升。

轴承指定点(θξ,zη,rζ)处温升在其附近点(θj,zk)所产生的热变形由下式计算：

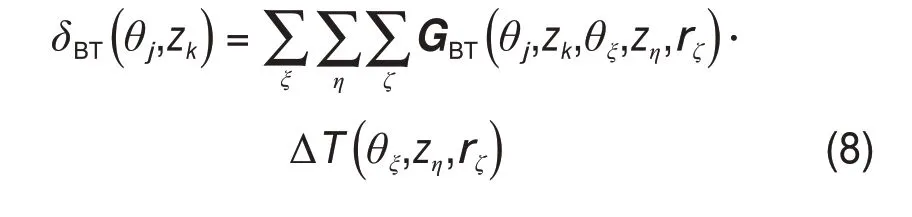
式中：δBT(θj,ΔTj)为轴承热膨胀；GBT(θj,zk,θξ,zη,rζ)为热变形影响系数矩阵；ΔT(θξ,zη,rζ)为指定点处温升。

1.4 微凸体接触模型

本文采用微凸体接触模型[20]表征平均膜厚和接触压力的关系。

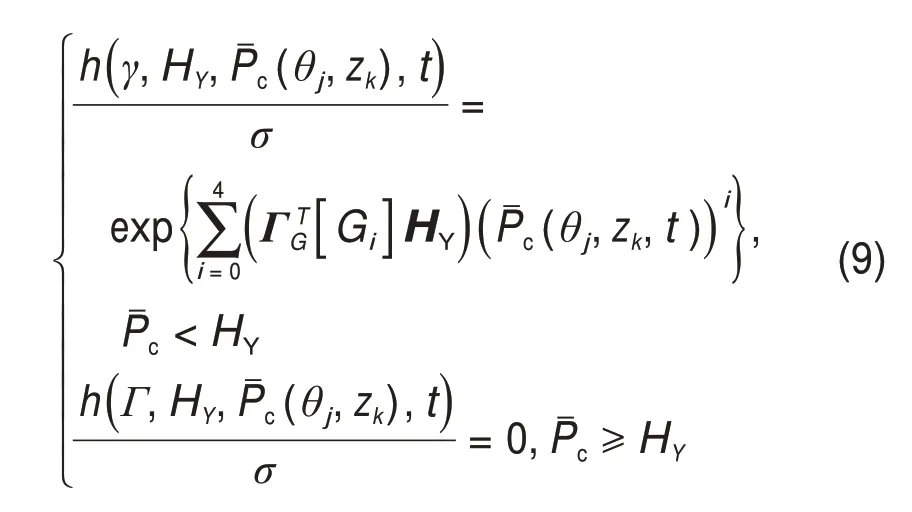
无量纲接触压力为

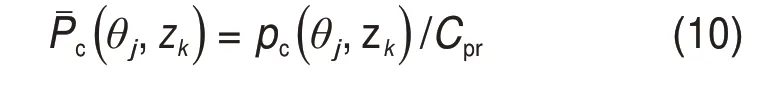
式中：Cpr为接触压力相对单位，Cpr=πHσ/(2λ)；H为轴瓦硬度；λ为摩擦副界面自相关长度；HY为轴瓦硬度参数，γ为摩擦副界面纹理参数；σ，H和γ的数值由表1和表2列出；[Gi]和HY由文献[20]给出。

1.5 承载力

在混合润滑状态下，ζ和κ方向上的承载力Fζ和Fκ(包括油膜力和接触力)方程如下：

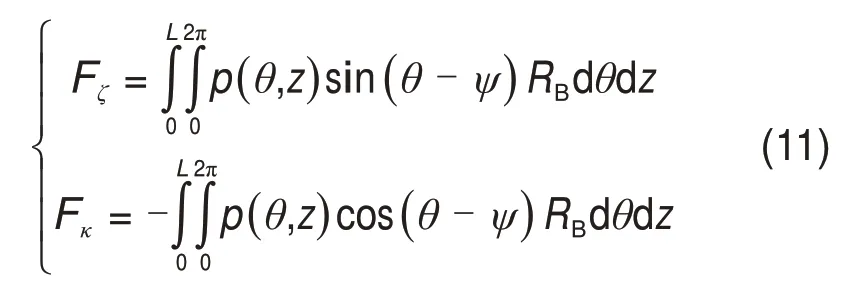
式中：RB为轴承内径。因此，轴承的总承载力W计算公式为

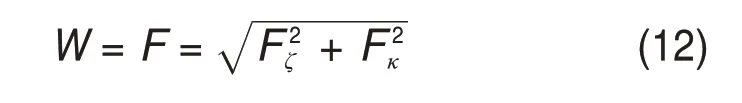
1.6 摩擦力和摩擦因数

混合润滑状态下，滑动轴承摩擦力f以及摩擦因数μ由下式计算：

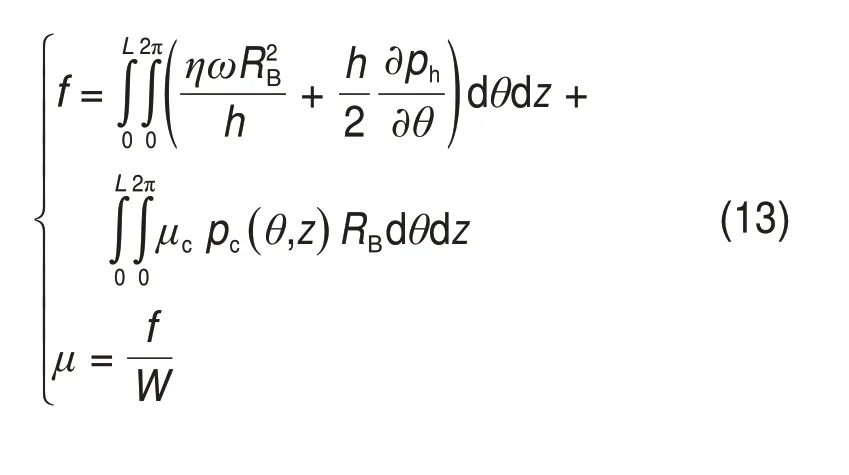
2 数值方法

2.1 计算流程

倾斜轴颈滑动轴承混合润滑数值模型仿真过程包括求解油膜压力、热(弹性)变形、粗糙接触压力和温度场等过程，其计算流程如图5所示。

由图5可知：数值计算循环迭代过程中涉及压力、偏位角以及JLB温度的收敛性判定。其收敛判定式如下：

式中：Fhζ和Fcζ分别为了ζ方向上的油膜力和接触力；Fhκ和Fcκ分别为κ方向上的油膜压力和接触力；和分别是轴、润滑介质和轴承结构的最高温度；和分别为上一迭代步节点和当前迭代步节点压力。

根据建立的混合热弹流润滑数值模型，对比分析滑动轴承在轴颈受载偏斜和轴颈对中工况下的混合热弹流性能。在本次数值模拟中，滑动轴承基本结构参数如表1所示，滑动轴承材料参数如表2所示，润滑油的特性参数如表3所示，轴与轴承热特性参数如表4所示。此外，粗糙峰接触模型中，轴径的粗糙度为0.2 μm，轴瓦的粗糙度为0.5 μm。

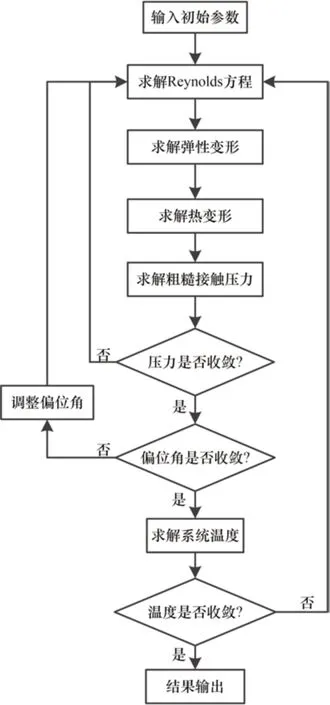
图5 计算流程图Fig.5 Flow chart for numerical calculation

表1 滑动轴承结构参数Table 1 Structural parameters of journal bearing mm

2.2 模型验证

为了验证本文数值方法的正确性，采用与文献[19]中试验轴承相同的结构参数与工况进行仿真计算，并比较试验和数值模拟下温度在周向方向上的变化规律，结果如图6所示。由图6可见：两者结果在上游区较吻合，而在下游区则存在微小差异，这是由于油膜厚度方向上采用了平均黏度，未计入黏度沿油膜厚度方向上的变化，导致数值仿真结果与实验结果存在差异[21]。

表2 滑动轴承材料参数Table 2 Material parameters of journal bearing

表3 润滑油特性参数Table 3 Characteristics parameters of the lubricating oil

表4 轴与轴承热特性参数Table 4 Thermal characteristic parameters of the journal and the journal bearing

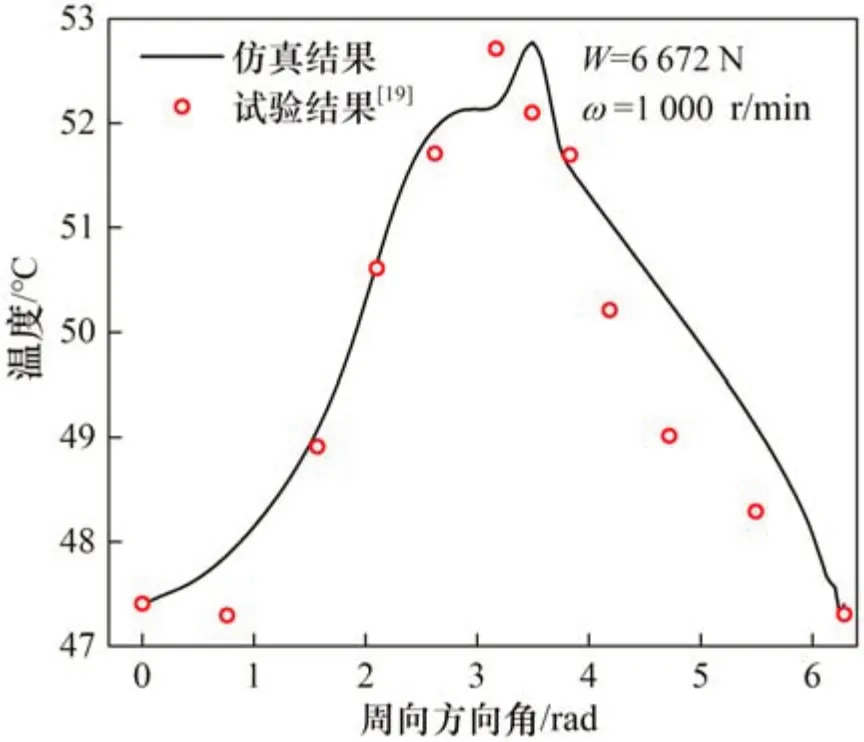
图6 数值仿真与试验结果的温度对比Fig.6 Comparison of the temperature between simulation results and experimental results

3 计算结果与讨论

3.1 滑动轴承混合润滑特性对比分析

本文给出1组滑动轴承混合热弹流润滑分析算例(工况条件为转速100 0 r/min，外载荷5 kN)，分别得到油膜压力、弹性变形和接触压力以及最小油膜厚度分布，如图7所示。

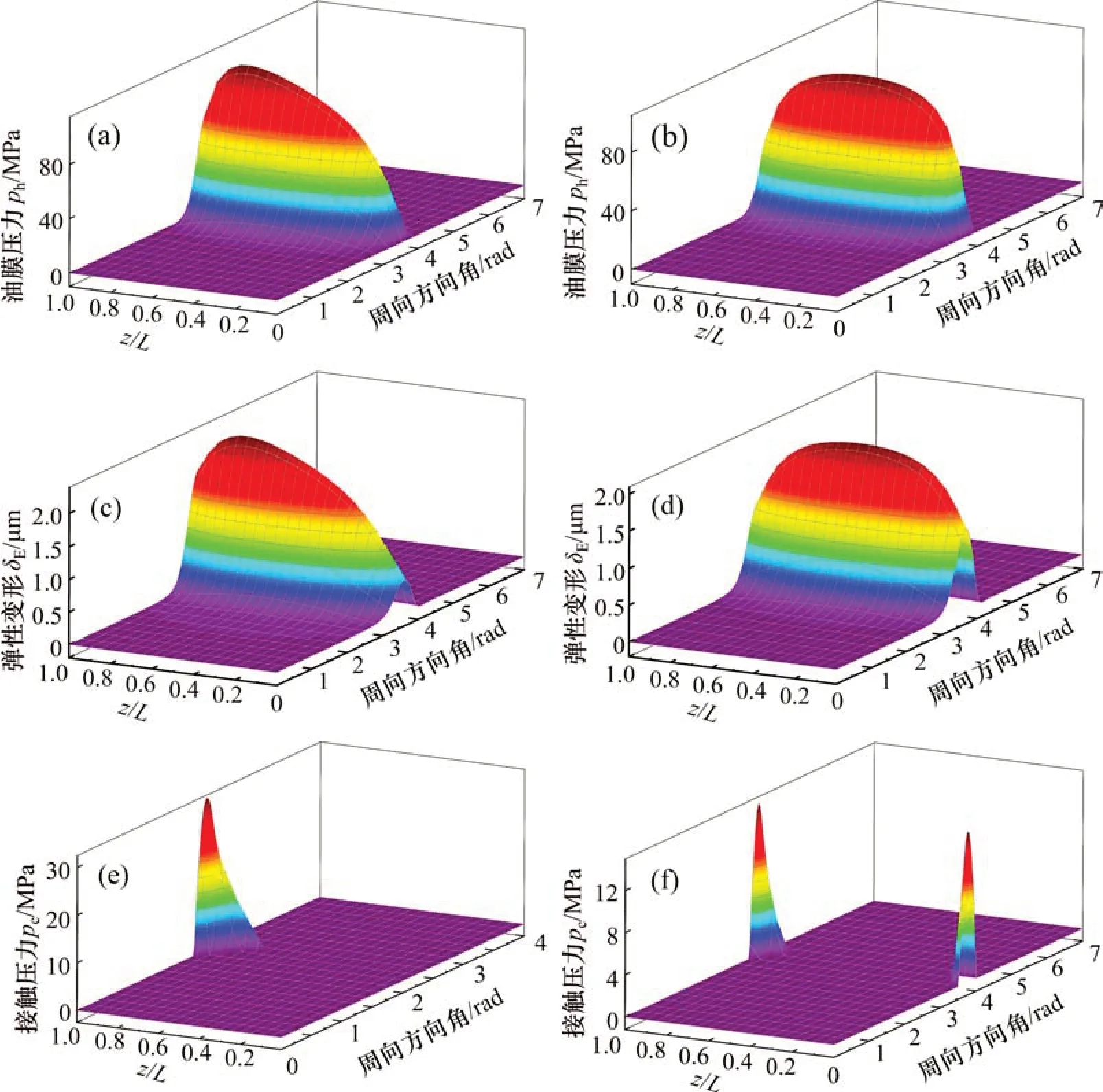
图7 油膜压力，弹性变形和接触压力分布Fig.7 Oil film pressure,elastic deformation and contact pressure distribution

由图7可知：相比于对中状态，轴颈受载倾斜使得油膜压力呈非对称分布，最大油膜力出现的位置向轴承末端偏移(边缘效应明显)，并且在油膜压力的作用下，弹性变形也表现出相同的分布规律；在对中状态下，由于润滑介质的端泄效应的影响，使得轴承两端油膜压力比中心部位的小，产生的弹性变形也相对较小，即轴承两端油膜厚度比中心部位的小，因此，轴承两端最先产生粗糙界面接触。而在轴颈倾斜作用下，轴承末端处油膜厚度会进一步减小，此时，轴颈与轴瓦只在末端发生接触，导致接触压力在这一局部区域内产生，其数值明显比对中状态的大。

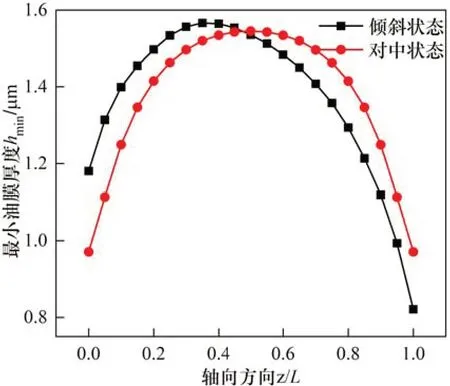
图8 最小油膜厚度分布曲线Fig.8 Distribution curves of minimum oil film thickness

3.2 JLB热特性对比分析

图9所示为JLB 的周向温度场特征(轴承末端最高温度处，径向截面)，图10所示为JLB的轴向温度场特征(轴承末端最高温度处，沿圆周方向的轴向切面)。由图9可见：轴、润滑介质和轴承轴瓦的温度分布具有连续性特征。轴承顶部开设供油槽，该处油膜温度等于供油温度(40°C)。在计入轴颈受载倾斜时，JLB 最高温度为63.50°C，要明显高于对中状态下的50.75°C，且最高温度均位于润滑介质-轴承轴瓦界面最小膜厚附近。此外，考虑轴颈受载倾斜时轴心与最小油膜处的温度梯度明显高于对中情况。因此，受载倾斜时温度沿径向的分布不均匀程度比对中状态下更加显著。从图9中还可以发现：在润滑油被轴颈由最小膜厚处卷吸到供油区的过程中，由于润滑油的热量耗散而呈现温度逐渐减小的趋势。

从图10可见：当轴处于对中状态时，最高油膜温度发生在轴承两端，这同样是由于润滑介质端泄效应的影响，使得轴承两端产生更大区域的粗糙峰接触。而当计入轴颈受载倾斜后，接触将集中于轴承末端，此时轴与轴承界面相比于对中状态会产生更大的接触压力，由此产生更高的摩擦热量和热变形，最终使得轴端间隙减小并进一步增加接触压力，并如此反复。从图10中还可以发现：轴颈受载倾斜时油膜温度明显比对中状态时的高，并且轴向的温度梯度也比对中状态时的高。

热变形分布特征(包括最高温度处轴向和周向热变形分布图)如图11所示。由图11可见：在倾斜状态下，热变形沿轴向分布呈现不对称性，这是轴颈受载倾斜时热量沿轴向不均匀产生的。另外，由于在最小膜厚处产生较为集中的接触压力，沿周向方向上的热变形在最小油膜处发生了明显的微凸现象。且在倾斜状态下，热变形明显大于对中状态下的热变形。

3.3 外载荷下混合热弹流特性影响分析

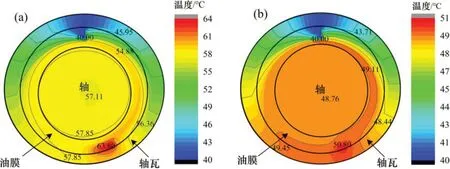
图9 JLB周向温度场特征Fig.9 Temperature field characteristics in JLB circumferential direction

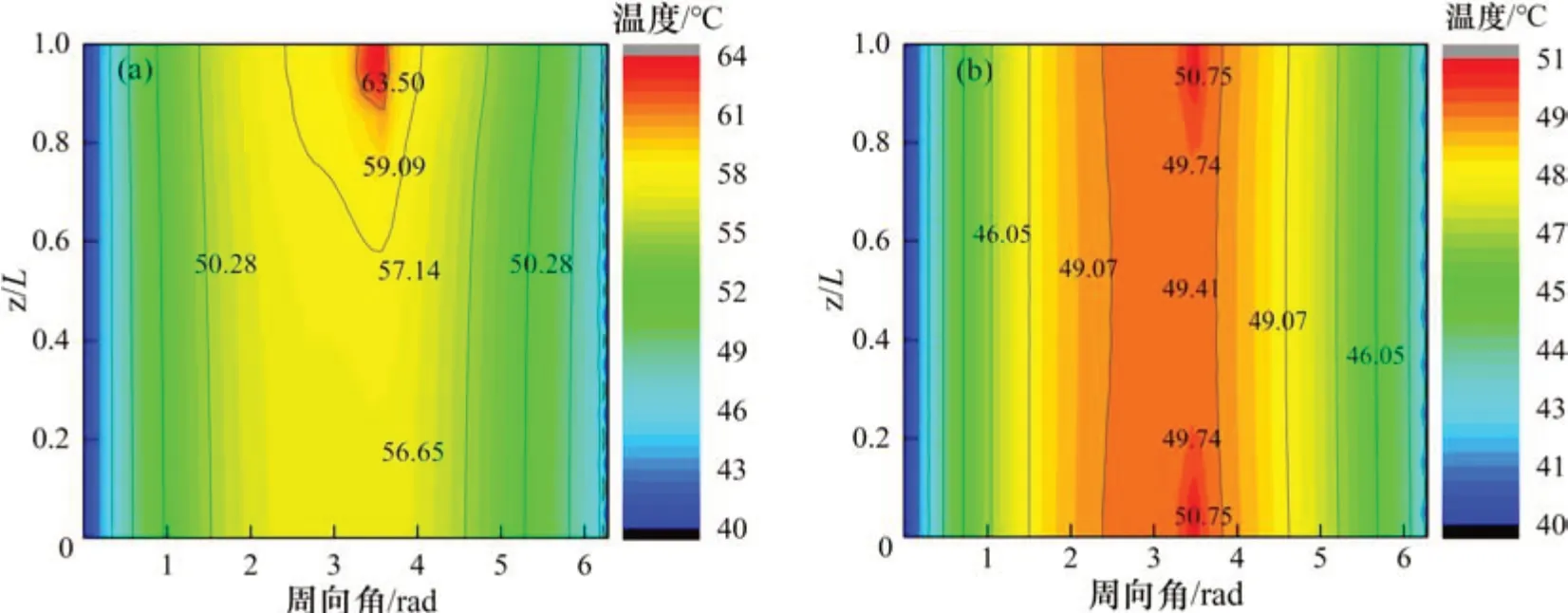
图10 JLB轴向温度场特征Fig.10 Temperature field characteristic of axial direction

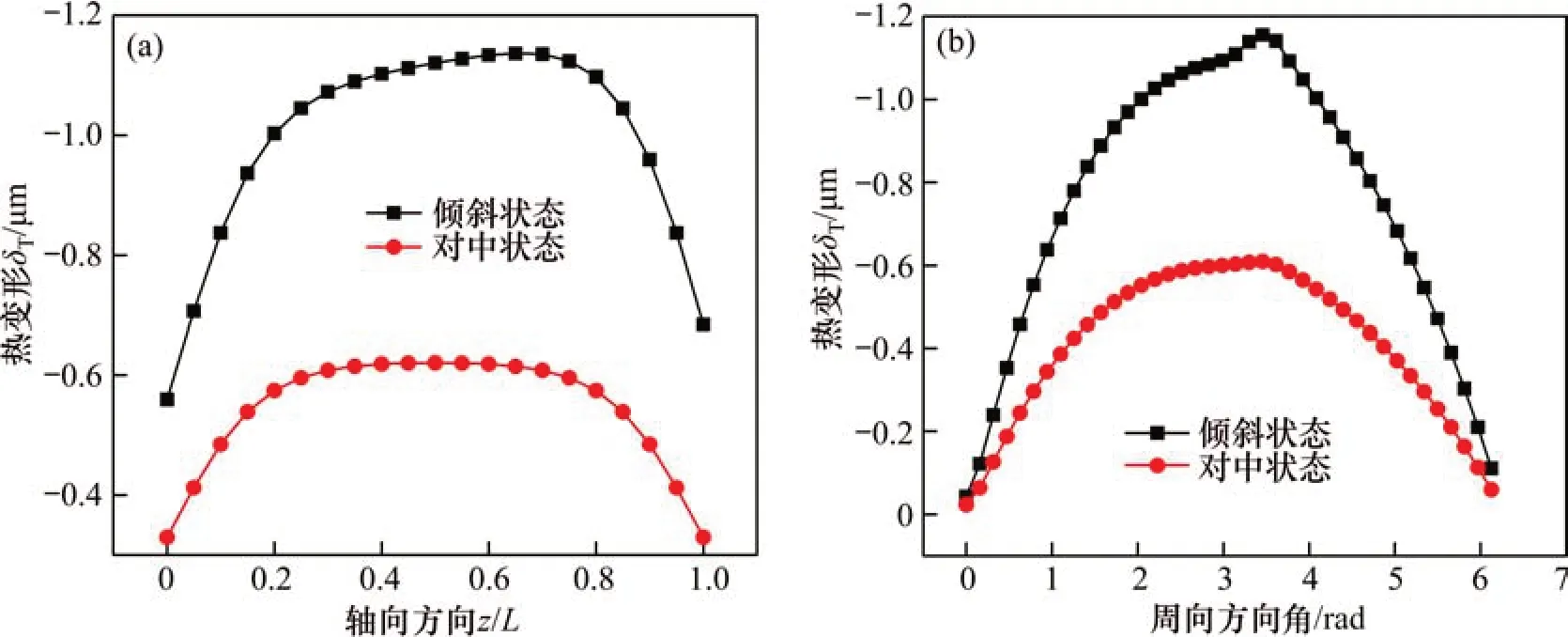
图11 热变形分布特征Fig.11 Thermal deformation distribution characteristic

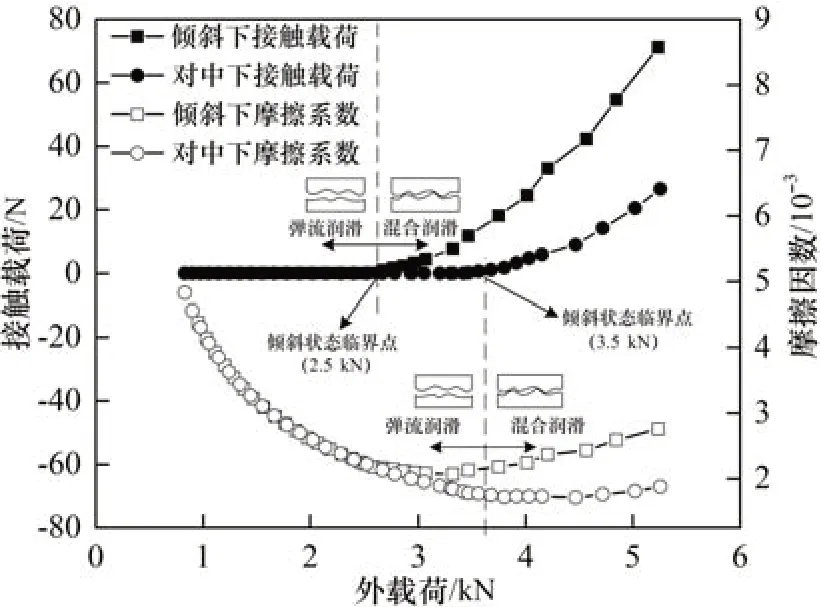
图12 接触载荷及摩擦因数随外载荷的变化规律Fig.12 Variation laws of contact load and friction coefficient with external load

图12所示为接触载荷及摩擦因数随荷载的变化规律。由图12可得：轴与轴承在轴颈倾斜状态下要先于对中状态发生固体接触，其临界点分别为2.5 kN(倾斜状态)和3.5 kN(对中状态)。随着载荷小于临界点，轴承处于全膜润滑状态，此时，摩擦力主要由油膜剪切力产生，其随着外载荷的增大呈现下降趋势，并且轴颈倾斜状态和对中状态下的摩擦因数差异很小，即在此阶段内轴颈倾斜对于摩擦因数的影响较微弱。当外载荷大于临界点时，轴承与轴发生接触，轴承处于混合润滑状态。随着外载荷进一步增大，接触压力呈现指数上升趋势，并且轴颈倾斜状态下的接触压力上升幅度也要明显比对中状态的大。另外，在轴颈倾斜状态下，轴承摩擦因数开始逐渐上升，而对中状态下的摩擦因数则基本保持不变。相较于对中状态，轴颈倾斜状态下轴承的最小油膜厚度明显减小，轴与轴承更易发生微凸体接触，接触区域更加集中，导致局部接触载荷更大，并且随着外载荷增加，热变形增大，进一步恶化轴承的润滑状态，接触载荷也会进一步增大。另外，由于在混合润滑状态下，摩擦力由油膜剪切力和微凸体接触力共同产生，因而，在相同外载荷条件下，接触载荷比(即接触载荷在总载荷中的占比)越大，摩擦因数也越大。

图13所示为最高油膜温度及最大热变形随外载荷的变化规律。由图13可见：当外载荷在小于3 kN 时，考虑轴颈倾斜和对中状态下的最高油膜温度与最大热膨胀变形呈现相同的变化规律，即最高油膜温度和最大热膨胀变形随着外载荷的增加而不断增大，因为在此阶段内，轴与轴承粗糙界面还未发生接触，即此时接触压力还很小，温升主要由动压油膜黏性滞耗产生，轴颈倾斜对油膜温度和热膨胀变形的影响比较微弱，所以，两者之间的区别较小。而当外载荷大于3 kN 时，随着外载荷的增加，最小膜厚区域逐渐变小，主要集中于轴承端部很小的区域，该区域内润滑状态急剧恶化，由图12可知，此时接触载荷显著增大，并且轴颈倾斜下的接触载荷要明显比对中状态的大，粗糙表面接触摩擦生热导致油膜最高温度呈现快速上升的趋势，而相应的最大热膨胀变形也随之显著增加。

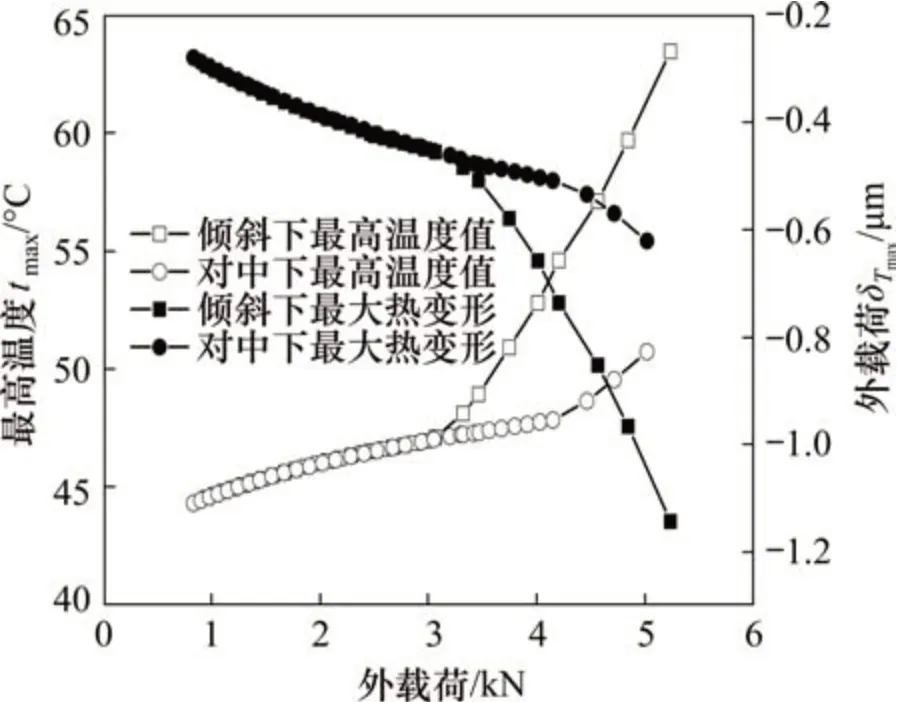
图13 最高油膜温度及最大热变形随外载荷的变化规律Fig.13 Variation laws of maximum oil film temperature and maximum thermal deformation with external load

4 结论

1)在对中状态下，接触压力发生在轴承两端，沿轴向对称分布，而轴颈在受载倾斜状态下，接触压力则集中于轴承末端，并且其最大接触压力约为对中状态下的2倍。

2)轴颈在受载倾斜状态下，JLB周向以及轴向温度场的不均匀性比对中状态的强，整体温度比对中状态的大。在倾斜状态下，沿油膜最高温度处的周向截面与轴向截面内热变形分布呈现非对称性，边缘效应明显，热变形也要高于对中状态的变形。

3)在弹流润滑阶段，轴颈受载倾斜及对中状态下的接触载荷、摩擦因数、JLB最高温度以及最大热变形数值之间的差异很小。在混合润滑状态，随着外载荷的增加，接触载荷、摩擦因数、JLB最高温度以及最大热变形均不断增大，但倾斜状态的增幅要明显大于对中状态的增幅。