一道中考题的多视角探究*

四川内江师范学院数学与信息科学学院 游 娇

四川内江师范学院数学与信息科学学院 罗力杰

四川内江师范学院数学与信息科学学院 刘成龙

中考试题立意深刻、设计独特、背景公平，具有典型性、示范性和公平性，是知识和数学素养的载体，直接反映了中考命题规律和动态.因此，中考试题是研究中考的最佳材料.如何研究中考试题呢？我们认为首要任务是选择恰当的视角.研究中考试题的视角很多，如解法、变式、背景、立意、规律等.本文中针对2018年成都中考第28题，从解法、背景和变式三个角度进行深入研究.

一、试题再现

试题：（2018年成都中考第28题，下文简称28题）如图1，在平面直角坐标系xOy中，以直线x=为对称轴的抛物线y=ax2+bx+c与直线l∶y=kx+m（k＞0）交于A（1，1）、B两点，与y轴交于点C（0，5），直线l与y轴交于点D.

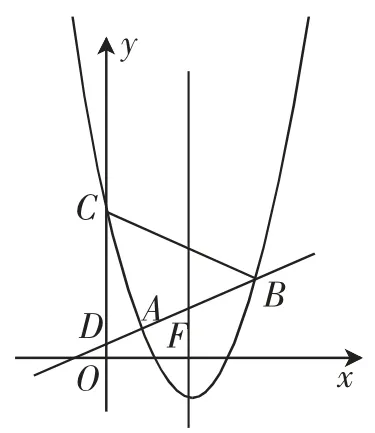
图1

（1）求抛物线的函数表达式.

（2）设直线l与抛物线的对称轴的交点为F，点G是抛物线上位于对称轴右侧的一点.若，且△BCG与△BCD面积相等，求点G的坐标.

（3）若在x轴上有且仅有一点P，使∠APB=90°，求k的值.

注：解（1）得y=x2-5x+5，过程略.

二、试题解法

在数学活动中，问题是研究的对象，而问题解决不仅是研究的目标，而且是最基本的数学活动形式.试题解法研究可以从一题多解和多题一解着手，从答题的典型失误和优美解、方法提炼、解题反思等视角展开.其中，一题多解指对试题从不同的路径，采用不同的方法进行研究，最终获得不同的解法［1］.试题多解的研究有利于沟通解法间的联系，有利于弄清试题的本质，有利于发掘试题的背景，有利于厘清试题的变式，有利于从不同角度领会命题者的意图.本文对28题（2）（3）进行多解研究.

1.（2）的多种解法

解法1：如图2，过点B作BT⊥x轴于点T，过点A作AM⊥l于点M，AE⊥BT于点E.

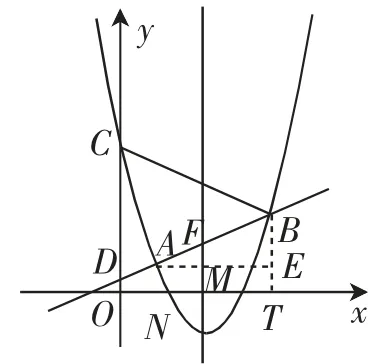
图2

由题意得点G的位置分为两种情形，如图3：

①点G在BC下方.

DG1∥BC，解得x=3，得出点G（3，-1）.

②点G在BC上方.

因为G2G3与DG1关于BC对称，所以

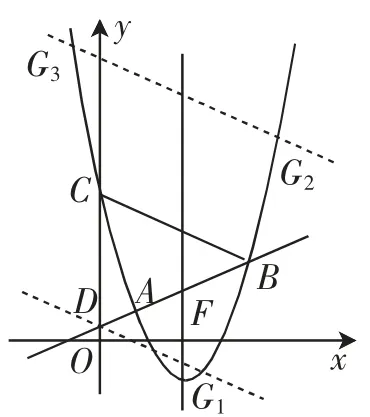
图3

解法2：设点

将点B的坐标代入y=x2-5x+5，解得k=，所以点得出直线BC的方程为下同解法1.

解法3：由解得x=k+4或x=1（舍去）.

所以点B（k+4，k2+3k+1）.又因为点，解得（舍去），所以得到点易知直线BC的方程为5.下同解法1.

解法4：如图4，作AM⊥x轴，BN⊥x轴，垂足分别为点M、N，记直线x=与x轴的交点为Q，则.因为MQ=，所以NQ=2，则点

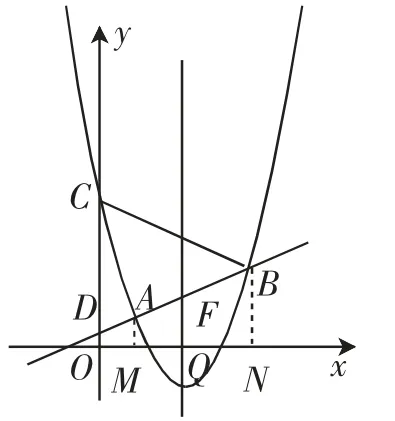
图4

下同解法1.

2.（3）的多种解法

解法1：如图5，由题意可知，点A的坐标为（1，1）.又点A在y=kx+m上，易得m=1-k，于是y=kx+1-k.

图5

解法2：同解法1，解得点B（k+4，k2+3k+1）.设点P的坐标为（n，0），则直线AP的方程为.因为∠APB=90°，所以AP⊥BP，得直线BP的方程为y=（n-1）x+n（1-n）.将点B的坐标代入，得n2-（k+5）n+k2+4k+5=0.因为点P有且只有一个，解得k=-1+

解法3：同解法1，解得点B（k+4，k2+3k+1）.设点P的坐标为（n，0），因为BA的中点为显然PO′则n2-（k+5）n+k2+4k+5=0，解得①.因为kAP·kBP=-1，所以=-1，则k2+3k+1=（n-1）·（k+4-n）②.将①代入②，得

解法4：同解法1，点A（1，1）、B（k+4，k2+3k+1）.设点P（n，0），由kAP·kBP=-1，得，解得n=.因为点P是唯一的，所以Δ=0，解得，所以点因为∠APB=90°，所以AB2=AP2+BP2，则3k2+6k-5=0，解得.又因为k＞0，所以k=-1+

三、试题变式

变式指相对于某种范式，不断变更问题情境或改变思维角度，使事物的非本质属性时隐时现，而事物的本质属性保持不变的变化方式［2］.变式可以有效抑制题海战术，而且能完善学生认知结构，使学生形成良好的认知能力.下面对28题（2）进行变式研究.

分析1：（2）中△BCG与△BCD面积相等这一条件能变成更一般的情形吗？

变式1：其他条件不变，将△BCG与△BCD的面积比改为，求点G的坐标.

解：已知点

（1）当点G在BC上方时，得直线G1G2的方程为解得点G的坐标为

（2）当点G在BC下方时，得直线G3G4的方程为解得点G的坐标为

分析2：（2）中这一条件能变成更一般的情形吗？

变式2：其他条件不变，设=λ，求点G的坐标.

解：如图4，过点B作BN⊥x轴于点N，得，即，解得，所以点又点A（1，1）在y=kx+m上，由解得，则直线直线

分析3：（2）中△BCD与△BCG面积相等和这两个条件能同时变成更一般的情形吗？（有兴趣的读者可以研究）

四、试题背景

试题背景指命题选材中涉及的知识、模型、思想、方法等.［2］研究试题背景对理解试题、把握试题本质有积极意义.常见的试题背景有很多，如现实生活背景、初中教材背景、中考试题背景、高中数学背景等.［2］28题蕴含丰富的高中数学背景，分析如下：

背景1：点到直线距离公式

分析1：（2）中△BCD与△BCG具有相同的边BC，而△BCD与△BCG面积相等等价于BC边上的高相等，即点G到BC的距离等于点D到BC的距离，则原问题转化为求到BC距离等于点D到BC距离的点G，显然试题含有点到直线距离这一背景.

点到直线距离公式：设直线方程Ax+By+C=0，点P的坐标为（x0，y0），则点P到直线的距离下面给出点到直线距离公式下的试题解答：

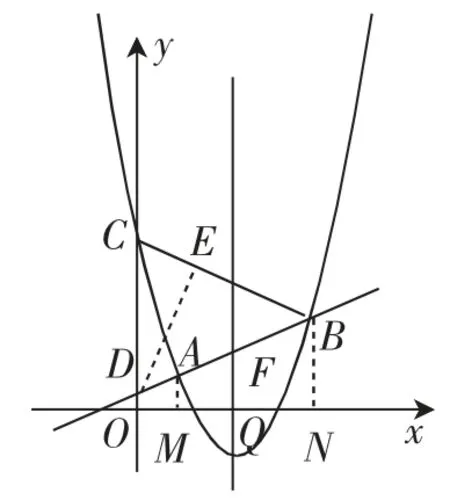
图6

解：如图6，设点G（x，x2-5x+5），过点D作DE⊥BC于点E，直线BC的方程为由S△BCD=解得DE=.又S△BCD=S△BCG，所以利用点到直线距离公式得出点G到直线BC的距离为

背景2：定比分点坐标公式.

分析2：（2）中将A、B、F三点联系在一起，从本质上讲这种联系是坐标间的联系，如何刻画呢？最直接的表征方式是向量的定比分点坐标公式.

定比分点坐标公式：设坐标轴上一有向线段的起点和终点的坐标分别为x1和x2，分点M分此有向线段的比为λ，那么，分点M的坐标

至于点B坐标的求解，可以运用定比分点坐标公式得到，如下：

数学家波利亚指出：一个有责任心的教师与其穷于应付烦琐的数学内容和过量的题目，还不如适当地选择某些有意义但又不太复杂的题目去帮助学生发掘题目的各个方面.［3］从多个方面对28题进行分析，可以深刻理解试题的本质、拓宽试题解法、加强试题变式，以达到举一反三、触类旁通.