挖掘学科素养，分析讨论方向——由一道中考试题说起

江苏省南京师范大学附属中学仙林分校初中部 曹玉梅

进入九年级下学期，学生面临的重要任务就是备考，一线教师也倍感压力，怎样才能做好中考备考引领工作？我校数学备课组成员群策群力，将备考专题进行了细致分解，在集体备课的基础上要求每位同仁都要分析整理一个中考试题类型.笔者整理的类型是分类讨论型试题.笔者认真分析了2018年江苏各地中考试题，寻找适合的试题，研究出一些相关的解题策略，让学生在备考中对这类试题进行再思考、再运用.

一、由分类讨论中考试题说起

例1（2018年南通市中考试题）在平面直角坐标系xOy中，已知抛物线y=x2-2（k-1）x+k2-k（k为常数）.

（1）若抛物线经过点（1，k2），求k的值.

（2）若抛物线经过点（2k，y1）和点（2，y2），且y1＞y2，求k的取值范围.

（3）将抛物线向右平移1个单位长度得到新抛物线，当1≤x≤2时，新抛物线对应的函数有最小值-，求k的值.

思路分析：第（1）、（2）问不是分类讨论，暂且略去.

对于第（3）问，首先利用顶点坐标的变化求出平移后抛物线的解析式，再将对称轴的位置和二次函数的增减性融合在一起，分三种情况讨论.

由抛物线y=x2-2（k-1）x+k2-，将抛物线向右平移1个单位长度，得到的新抛物线的解析式为y=（x-k）2-即可得出新抛物线的对称轴为直线x=k.

通过上述讨论，可知k的值为1或3.

例题2：（2018年莱芜市中考试题）如图1，边长为2的正△ABC的边BC在直线l上，两条距离为1的平行直线a和b垂直于直线l，a和b同时向右移动（a的起始位置为点B），速度均为每秒1个单位，运动时间为t（秒），直到b到达点C停止.在a和b向右移动的过程中，记△ABC夹在a和b之间的部分的面积为s，则s关于t的函数图像大致为（ ）.

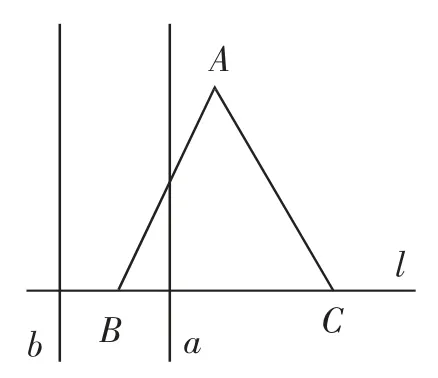
图1

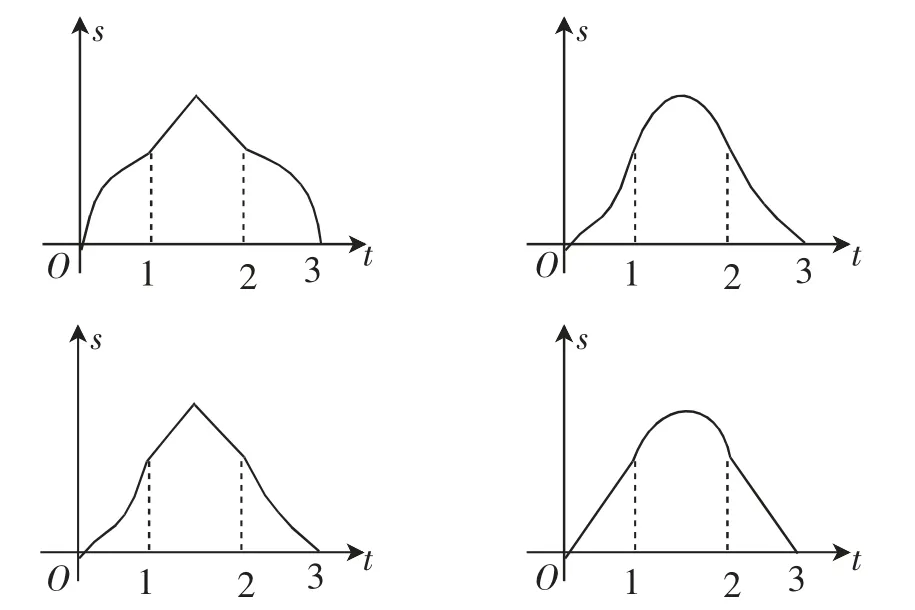
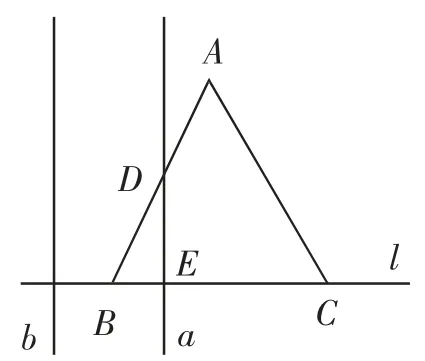
图2

思路分析：由题意知a和b同时向右移动，可以分三种情况进行讨论，分别求得函数解析式.

如图3，当1≤t＜2时，BG=t-1，CE=2-t.可以计算出

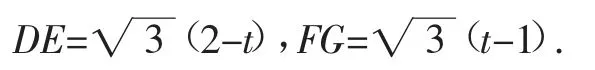
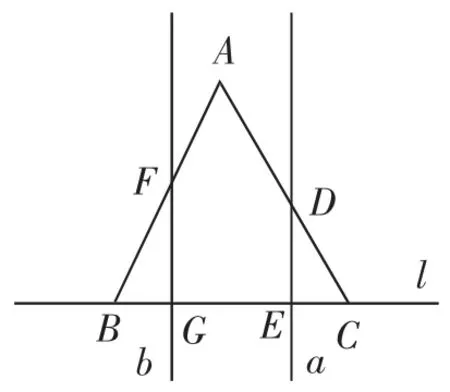
图3

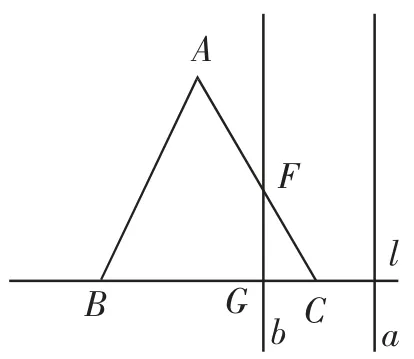
图4

通过以上函数图像的判断，所求图像由三段抛物线构成，分别是开口向上、开口向下、开口向上的三段抛物线.因此，本题选择B.

二、对分类讨论中考试题的思考

在初中阶段解决数学问题时，必须采取科学、快捷的做法，确保试题能够得到精准、完整解答，这就是数学学科核心素养.为了在中考试卷中突出数学学科核心素养，命题时会结合初中数学的主干知识，考查一些需要进行多角度思考的数学问题，其回答过程需要采取分类讨论的思路.

1.对案例的分析

回顾前面的案例，例1的第（3）问首先要找出k值的关键节点，因为得到的二次函数是，曲线是抛物线，对称轴为直线x=k，进行分段讨论时就必须从二次函数图像的对称轴x=k入手讨论取值区间，结合题干给出的信息1≤x≤2，再思考在整个取值区间内二次函数的最值情况.

例2 考查动点的函数图像判断，函数图像是典型的数形结合的应用.其分类讨论的起点是B，终点是C，关键点是A，以点A作为直线a和b运动的分界点，直线a到点A的时间t=1，直线b到点A的时间t=2.找到了时间节点，答案自然就出来了.

通过以上两个案例不难发现，作为涉及的不同层面或不同多角度的数学问题的解答，只有经过分类讨论，才能够做到精准，才能使得答案更加简便、完整.

2.分类讨论试题的解题策略

教学实践发现，分类讨论是数学题型中的常客，也是学生得分率较低的一种题型，因为初中生的智能特点使得做小题时经常忽视分类讨论，做大题时经常在讨论中丢三落四.在集体备课或者与学生交流时发现，许多成绩优异的学生也会栽在这种题型上，总是或多或少出现问题，因此在备考的过程中需要养成良好的解题习惯：

第一，树立分类讨论的意识.很多数学知识点是分类讨论的载体，可以将这些这些知识点罗列出来，增强学生的敏感性，警钟长鸣才能不落俗套.

第二，对分类讨论进行建模，不要抓住芝麻丢掉西瓜，通过建模让讨论在节点上具有连续性.这就要求学生做到：分类的标准是一致的，分类中的每一区间是相互独立的，分类讨论是逐级有序进行的.

第三，要求学生完整地列出所有需要讨论的可能性，然后仔细分析每种可能性是否都会存在，进行关键性的取舍.同样，对于某些问题，还需要注意是否有些讨论结果重复，相同的部分需要合并处理.

总之，分类讨论是一种十分重要的解决初中数学问题的思路.在解决这种类型的数学问题时，唯有教师针对知识内容和学情，进行合理建模，帮助学生熟练掌握分类讨论的解题思路；也唯有学生针对题目进行科学解答，及时有效地采取分类讨论，才能够清楚地分辨出数学问题的不同所在，才能够及时采取有效的解答问题的方案，才能使科学建模为我所用.