一道中考试题的赏析及教学启示*
(金华市外国语学校,浙江 金华 321015)
●徐灵姬
(西苑中学,浙江 金华 321017)
2019年浙江省金华市数学中考第23题将正方形与抛物线较好结合,数中有形,以形助数,数形结合.先根据确定的抛物线,求出好点个数,数中有形;再根据好点个数恰好为8个,确定抛物线要满足的条件,以形助数.这种浑然天成的命题布局彰显出中考压轴题的精致与灵活.
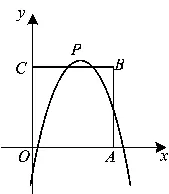
图1
1 试题呈现
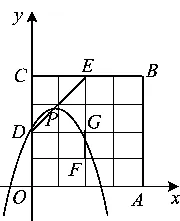
例1如图1,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴、y轴的正半轴上,把正方形OABC的内部及边上,横、纵坐标均为整数的点称为“好点”.点P为抛物线y=-(x-m)2+m+2的顶点.
1)当m=0时,求该抛物线下方(包括边界)的好点个数;
2)当m=3时,求该抛物线上的好点坐标;
3)若点P在正方形OABC内部,该抛物线下方(包括边界)恰好存在8个好点,求m的取值范围.
(2019年浙江省金华市数学中考试题第23题)
2 试题赏析
解1)当m=0时,y=-x2+2,画出图像(如图2).当x=0时,y=2;当x=1时,y=1.因此,可求该抛物线下方(包括边界)的好点有5个,分别是(0,0),(0,1),(0,2),(1,0),(1,1).
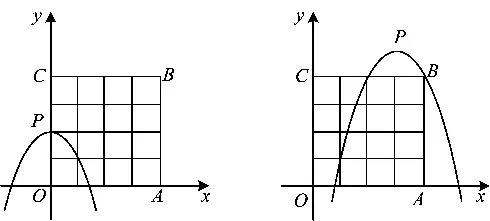
图2 图3
2)当m=3时,y=-(x-3)2+5,画出图像(如图3).当x=1时,y=1;当x=2时,y=4;当x=4时,y=4.因此,该抛物线上的好点坐标分别是(1,1),(2,4)和(4,4).
前两个小题都赋予了m特殊的值,直接代入二次函数解析式,画出图像,从而完成解答,解法自然生成.
对于第3)小题,先作如下思考:
问题1观察第1)和第2)小题画出的抛物线,有何共同特征?
观察发现两个抛物线的位置不同,但形状一样.抛物线y=-(x-m)2+m+2的二次项系数为-1.随着m的变化,抛物线的位置发生改变,但形状和开口方向都不变,即可通过平移得到.
这是浙教版《数学》九年级上册第11页第1.2.2节二次函数的内容.

图4
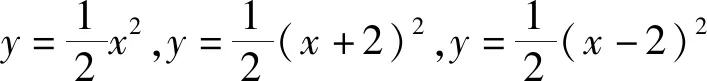
问题2点P的坐标是什么?可得什么信息?
由题目可知,点P(m,m+2)为抛物线y=-(x-m)2+m+2的顶点.观察点P的横、纵坐标,发现点P定在直线y=x+2上,随着m的变化,点P在这条直线上运动.
问题3点P在正方形OABC的内部,说明了什么?
2.出台针对基层统战干部的表彰奖励制度。为保证统战干部对统战对象、统战工作的熟悉度,应鼓励其长期从事基层统战工作。为此,应建立基层统战干部“功勋奖励”机制,可考虑经由中央统战部会同组织人事部门对长期从事基层统战工作并取得成绩的党员干部发放纪念章或勋章,对在统战工作某个领域取得突出成绩的“优秀统战干部”予以单项表彰,并作为统战干部年度考核、评先选优、职级晋升的重要依据。
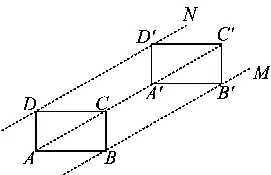
点P(m,2m)在正方形OABC的内部,则0 图5 综合以上信息,我们要研究的抛物线只要让顶点在线段DE(不包括端点)上平移即可,如图5. 问题4先画哪条抛物线?用什么办法平移呢? 根据浙教版《数学》七年级下册第22页第1.5节平行线的内容: 例2把长方形ABCD沿箭头所指的方向平移,使点C落在点C′(如图6),画出经这一平移后所得的图形. 图6 图7 图8 方法1如图7,将透明纸覆盖在长方形ABCD上,画出相同的图形,然后把透明纸沿箭头所指的方向平移,直到点C与点C′重合(如图8).长方形A′B′C′D′就是长方形ABCD经平移后得到的图形. 图9 根据以上方法,只需将透明纸覆盖在图1上,画出抛物线,然后把透明纸沿DE方向平移,观察好点个数即可. 图10 通过数形结合、平移、从特殊到一般、分析临界状态等方法,还可以解决好点为其他个数时的情况,做到触类旁通,有效地解决此类问题. 不管中考题如何呈现,命题的知识点和思想方法都以课本为基准,进行合理综合、拓展延伸.因此,教师平时的课堂教学要充分利用教材,深入研究教材及课程标准,领会教材编写意图,前后知识做到融会贯通.在教学过程中,将教材作用最大化. 例如,平移这节课的例题教学,课本提供了两种方法:1)实际操作法,用透明纸覆盖、画出相同长方形、平移、再画出平移后的图形;2)用作图的方法,先画出长方形4个顶点平移后的顶点,再依次连接起来.两种方法能发散学生的思维,让他们领会解决问题方法的多样性,从而解决平移问题.但有些教师往往会觉得实际操作法简单,而第二种是平移作图的基本方法,非常重要;教师容易忽略实际操作法,直接学习或着重讲解第二种方法.这就降低了例1第3)小题的得分率,是没有充分挖掘教材的后果. 《义务教育数学课程标准(2011年版)》明确提出:要处理好教师讲授与学生自主学习的关系,注重启发学生积极思考.有思考、有参与、有体验的学习才会记忆深刻,更加具有创造力.比如例1中的点P(m,m+2),教师可以通过以下问题引导学生思考:1)观察点P的横、纵坐标,你有什么发现?2)你是如何发现的,能进行验证吗?3)你能确定点P的位置吗……如果平时我们都通过问题引导学生思考,开展教学,那么学生肯定更有兴趣,能积极参与到数学活动中来. 现在是素质教育的时代,搞题海战术肯定是行不通的.作为教师,在平时的教学活动中,要有计划、有意识地渗透数学思想方法,这样才能让学生学会分析与解决问题,增强学生的创造力.比如例1中求取值范围问题:1)要确定一个范围,最重要的是确定什么?2)要确定临界值,要先画出临界状态,请你画一画.3)这种临界状态有何特征?4)过点F,对m有什么要求……通过这样的教学,渗透了求临界值法确定范围和数形结合的思想方法,随着方法的积累,学生自然看到问题,方法水到渠成. 如今不管是平时上数学课,还是出各种试卷,几何画板软件已经非常普及,只要画好图形,根据题意,变化位置,就可以编制出压轴题.在动态过程中,各种情形马上显现,对解题有着巨大帮助.但一看压轴题,就利用几何画板分析,学生缺少了画图、观察、猜测、计算、思考、推理、验证、探索等独立活动过程,对学生的思维发展是十分不利的.因此,在学生的学习阶段,几何画板软件适合在学生分析解决问题之后,作为辅助工具,让学生进行观察,更好地明白动态过程,对自己的分析结果作一个检验,从而体会分类讨论的完整性.对于函数图像教学,也是如此.先让学生自己动手画,随着点的增多,感受图像的形状,有了体会之后,再利用几何画板.这样利用软件,学生的学习会更加深刻. 学习是为了更好的生活,解决生活中出现的问题并且进行创新,培养学生的综合能力显得尤为重要.在数学教学中,我们要让学生学会看书、学会自学、学会独立思考,如果有问题,大胆地表达出自己的想法,要学会交流、学会合作,养成良好的学习习惯,运用数学的思维去进行思考,增强发现和提出问题、分析和解决问题的能力.

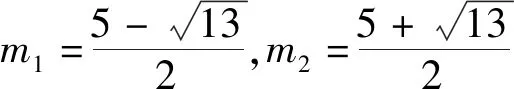
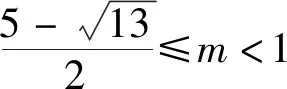
3 教学启示
3.1 充分挖掘教材
3.2 积极引导思考
3.3 注重渗透方法
3.4 合理利用软件
3.5 培养综合能力

