巧用函数观“点” 提升数学素养*

(金华市技师学院，浙江 金华 321017)

数学核心素养是课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用过程中逐步形成和发展的[1].本文以函数经典题型为载体，以数学思想方法为依托，以数学能力为特征，探究函数解题的通性通法.笔者通过自己的教学发现，要突破某些函数“重点与难点”问题，必须抓住一些关键的“点”，比如切线问题(切点未知的情况下)要设“切点”，最值问题围绕“零点”“极值点”和“端点”展开研究.把握这些“特殊点”，对培养学生“从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系”的数学核心素养有很大的帮助.

图1

1 极值问题防“拐点”

拐点的定义一般地，设y=f(x)在区间上I连续，x0是I的内点(除端点外的I内的点).如果曲线y=f(x)在经过点(x0,f(x0))时，曲线的凹凸性改变了，那么就称点(x0,f(x0))为该曲线的拐点[2].拐点在数学领域是指凸曲线与凹曲线的连接点(如图1所示).

对于高中生来说，不需要了解拐点的严格定义，但是需要清楚“f′(x0)=0”是“x0为函数y=f(x)的极值点”的必要非充分条件.不理解这个道理，学生在解相关问题时，逻辑推理不够严谨容易犯错.

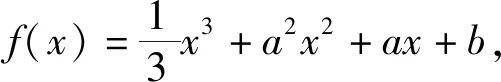
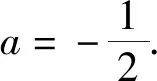
因为a有两个解，所以导致部分学生做出f(2)有两个解的误判.事实上，当a=1时，

f′(x)=(x+1)2≥0，

从而f(x)单调递增，不可能有极值.因此，极值问题一定要防“拐点”，正确运用“f′(x0)=0”是“x0为函数y=f(x)的极值点”的必要非充分条件，以免解题时造成不必要的错误.

解因为f′(x)=x2+2a2x+a，由题设知

f′(-1)=-2a2+a+1=0，

解得

当a=1时,f′(x)=x2+2x+1=(x+1)2≥0,从而f(x)在R上是增函数，没有极值.

解得

b=-1，

故

2 切线问题设“切点”

对于切线问题，以下例2中的3个小题非常具有代表性.

例21)曲线g(x)=ex-2在点(0,-1)处的切线方程是______．

2)过点(0,-1)作曲线f(x)=lnx的切线，则切线方程是______．

3)求与曲线f(x)=lnx和曲线g(x)=ex-2都相切的直线方程.

分析对于第1)小题,由已知切点(0,-1),求出g′(0)=1，便可得切线方程为y=x-1.

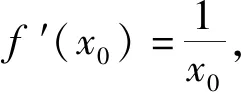
第3)小题是第1)和第2)小题的拓展，两个切点都未知.设曲线f(x)=lnx上的切点为(x1,lnx1)，则切线方程可表示为

同理曲线g(x)=ex-2上的切点为(x2,ex2-2)，则切线为

y=ex2(x-x2)+ex2-2.

由公切线知两切线的斜率相等、截距相等，得到关于x1,x2的方程组

将式(1)代入式(2)，消去x2可得

从而

解得

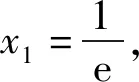
故切线方程是y=ex-2与y=x-1.

该题可以用如图2所示的思维导图来清楚地解释切线问题.

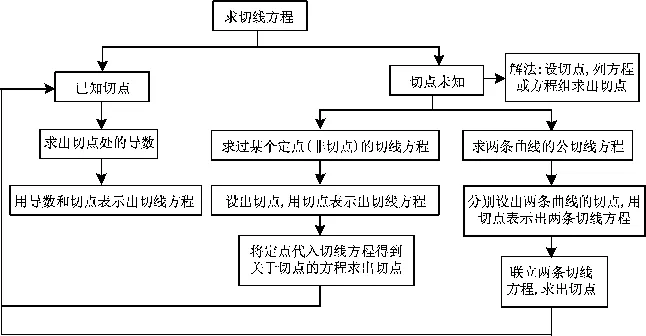
图2

总之，对于已知切点的问题可通过求出切点处的导数求出切线方程；对于切点未知的问题只要“设切点”，列出关于切点的方程，求出切点便可求出切线.

3 最值问题踩“两点”

函数的最值主要是在“端点”处的值和“极值点”处的值取到，从而这里的两点指的是“极值点”和“端点”.

分析f(x)的图像不经过第四象限，即f(x)≥0在x∈[0,+∞)上恒成立,从而

1)当a<0时，f′(x)>0,得f(x)在[0,+∞)上单调递增，f(x)≥f(0)=0，从而f(x)在端点处取到最小值，符合题意.

2)当a>0时，因为x∈[0,+∞)，所以

即

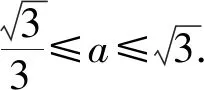
围绕“端点”和“极值点”展开研究，在“当a>0时”的情况下抓住这两点,减少了对单调性的讨论研究，使得解题更加便利.

4 负分布破“零点”

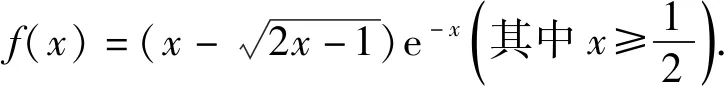
1)求f(x)的导函数；

分析1)略.

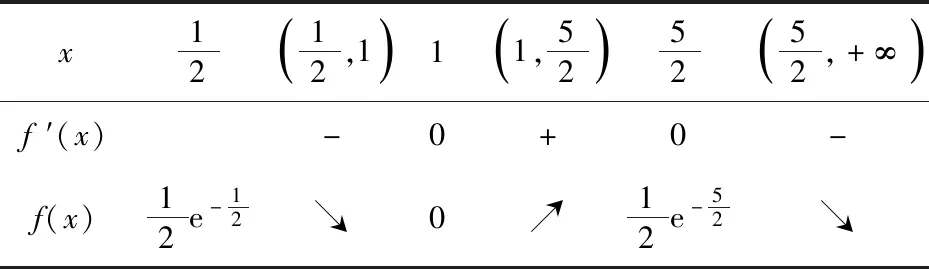
表1 f(x)，f ′(x)随x的变化情况

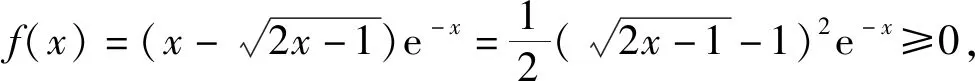
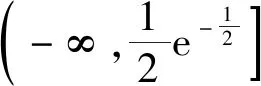
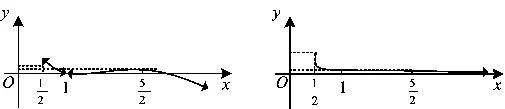
图3 图4

面对经济、科技的迅猛发展和社会的深刻变化，面对国际竞争提升的需求，新时代呼唤优秀的数学人才.而高中数学是基础学科，承载着塑造“通过运算促进数学思维发展，形成规范思考问题的品质，发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题”能力的新一代重任.当下，以数学素养为核心的教学改革工作正在全面展开，坚守“数学教学是数学思维的教学”和“数学能力是在不断践行解决数学问题中形成”的理念，科学处理好数学教学中“讲”与“练”的关系，是教学实践向提升数学素养转化最现实的问题.本文旨在培育学生运用“从特殊到一般”的推理方法解决函数问题，学会抓住关键“点”，从“点”窥视函数的特征，从而减轻学习负担，提升学习效率.