探析中考图形变化规律问题的求解策略

摘 要：本文从循环规律的图形变化类型、旋转规律的图形变化类型、相似比例规律的图形变化类型、跨学科规律的图形变化类型四方面，通过例题详解，得出解决这类问题的直接方法是根据各自特点，分析总结由图形的变化所带来的数据变化的规律，总结出通项公式，从而找到解决问题的途径.

关键词：图形变化; 规律问题;求解策略

作者简介：刘恩举（1969-），男，甘肃酒泉人，本科，中学一级教师，研究方向：中学数学教学.

1 按循环规律的图形变化类型

例1 如图1，Rt△OA1C1，Rt△OA2C2，Rt△OA3C3，Rt△OA4C4……斜边均在平面直角坐标系，xOy的坐标轴上∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°，OA1=OC2，OA2=OC3，OA3=OC4…，依此规律变化，若已知A1（3，0），则点A2014的纵坐标为（ ）.

A. （2 3）2014B.-3×2 332013

C.0D.3×2 332013

解析 根据题意可知，在Rt△OA2C2中，OC2= OA1=3，∠A2OC2=30°，所以OA2=23OC2=3×2 33.

同理Rt△OA3C3，OC3= OA2=3×2 33.

所以OA3=23OC3=3×（2 33）2.

同理Rt△OA4C4，OC4= OA3=3×（2 33）2.

所以OA4=23OC4=3×（2 33）3.

所以OA2014=23OC2014=3×（2 33）2013.

根据2014=4×503+2，可判定A2014在y轴的正半轴上，A2014的纵坐标为3×（2 33）2013，选D.

评注 本题图形的变化是循环变化的，抓住含30度直角三角形的性质，应用直角三角形中斜边与直角边的关系，总结出An的纵坐标的变化规律，就能得到方法，解决问题.

2 按旋转规律的图形变化类型

例2 平面直角坐标系xOy中，关于点B1作边长为2的等边△OA1B1的中心对称图形△B2A2B1，再关于点B2作△B2A2B1的中心對称图形△B2A3B3，如此反复作下去，n是正整数，A2n+1是△B2nA2n+1B2n+1的顶点，由此可知A2n+1的坐标（ ）.

A.（2n-1，3）B.（4n-1，3）

C.（4n+1，3）D.（2n+1，3）

解析 根据题意，由等边△OA1B1的边长为2，可知A1（1， 3），B1（2， 0）.

△B2A2B1是△OA1B1关于点B1的中心对称图形，点A2是点A1关于点B1的中心对称点，所以2×2-1=3，2×0-3=-3，因此点A2（3， -3）.

同理，△B2A3B3是△B2A2B1关于点B2的中心对称图形，点A3是点A2关于点B2的中心对称点，所以2×4-3=5，2×0-（-3）=3，因此点A3（5， 3）.

同理，△B3A4B4是△B2A3B3关于点B3的中心对称图形，点A4是点A3关于点B2的中心对称点，所以2×6-5=7，2×0-3=-3，因此点A4（7， -3）.

由以上推理总结：1=2×1-1，3=2×2-1，5=2×3-1，7=2×3-1，….

可得An的横坐标是2n-1，A2n+1的横坐标就可知是2（2n+1）-1=4n+1.

从以上分析，n为奇数时，An的纵坐标是3;n为偶数时，An的纵坐标是-3.

由于2n+1是奇数，由此可知顶点A2n+1的纵坐标是3.因此△B2nA2n+1B2n+1（n是正整数）的顶点A2n+1（4n+1，3），答案为C.

评注 本题中图形的变化是不断作等边三角形右侧顶点的对称图形，实际是关于右侧顶点旋转所得，因此抓住旋转之后坐标的联系，写出另外两个顶点的坐标，观察规律，总结出通项表达式，就会使问题突破.

3 按相似比例规律的图形变化类型

例3 如图3所示，平面直角坐标系xOy中有直线y=2x，过x轴上的点A1，A2，A3，…，An，An+1作x轴的垂线交直线y=2x于点B1，B2，B3，…，Bn，Bn+1，已知OA1=A1A2=A2A3=…=AnAn+1=1，连接A1B2，B1A2，B2A3，…，AnBn+1，BnAn+1，相互之间依次相交于点P1，P2，P3，…，Pn，形成的△A1B1P1，△A2B2P2，…，△AnBnPn…，它们的面积依次记为S1，S2，S3，…，Sn，则Sn为（ ）.

A. n3n-1 B.n+12n+1

C.n22n-1 D.n22n+1

解析 根据题意，过x轴上的点A1，A2，A3，…，An，An+1作x轴的垂线交直线y=2x于点B1，B2，B3，…，Bn，Bn+1，知OA1=A1A2=A2A3=…=AnAn+1=1.

由此可知点B1的横坐标为1，点B1是直线y=2x上的点，将x=1代入y=2x可得点B1的纵坐标为2，即B1（1，2）.

同理可知点B2的横坐标为2，点B2的纵坐标为4，即B2（2，4）.

类推可知，B3（3，6），…，Bn（n，2n）.

因为A1B1//A2B2，所以ΔA1B1P1∽ΔA2B2P1.

所以A1B1A2B2=12.

所以△A1B1P1与△A2B2P1对应高的比为1∶2.

因为两高之和为A1A2=1，所以△A1B1P1在A1B1边上的高为13，所以△A1B1P1的面积S1=12×2×13=13=122×1+1.

同理，因为A2B2A3B3=46=23，所以△A2B2P2与△A3B3P2对应高的比为2∶3.

因为两高之和为A2A3=1，所以△A2B2P2在A2B2边上的高为25，△A2B2P2的面积S2=12×4×25=45=222×2+1.

依次类推，S3=97=322×3+1，…，Sn=n22n+1，选D.

评注 图形按相似变化发展，要灵活运用直线上点的坐标与方程的关系，将横坐标代入直线解析式，可得直线上点的纵坐标，得出所求三角形的面积，根据相似三角形对应边成比例，总结出面积的通项表达式，即可求解.

4 按跨学科规律的图形变化类型

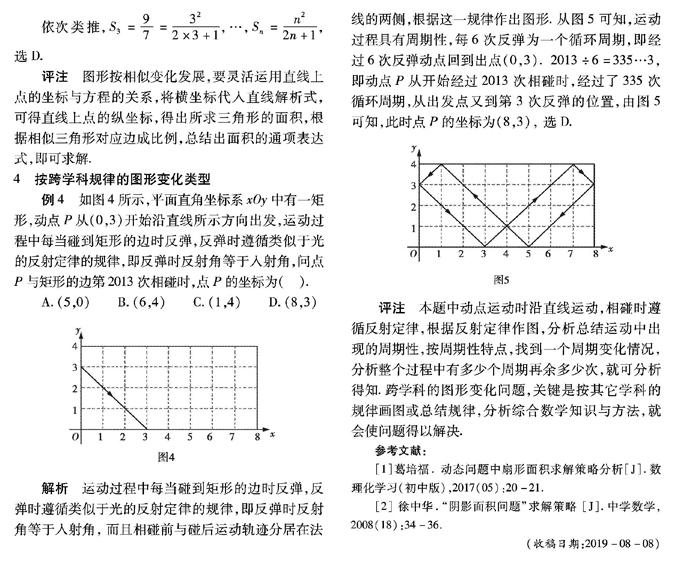
例4 如图4所示，平面直角坐标系xOy中有一矩形，动点P从（0，3）开始沿直线所示方向出发，运动过程中每当碰到矩形的边时反弹，反弹时遵循类似于光的反射定律的规律，即反弹时反射角等于入射角，问点P与矩形的边第2013次相碰时，点P的坐标为（ ）.

A.（5，0）B.（6，4）C.（1，4）D.（8，3）

解析 运动过程中每当碰到矩形的边时反弹，反弹时遵循类似于光的反射定律的规律，即反弹时反射角等于入射角，而且相碰前与碰后运动轨迹分居在法线的两侧，根据这一规律作出图形.从图5可知，运动过程具有周期性，每6次反弹为一个循环周期，即经过6次反弹动点回到出点（0，3）. 2013÷6=335…3，即动点P从开始经过2013次相碰时，经过了335次循环周期，从出发点又到第3次反弹的位置，由图5可知，此时点P的坐标为（8，3）， 选D.

评注 本题中动点运动时沿直线运动，相碰时遵循反射定律，根据反射定律作图，分析总结运动中出现的周期性，按周期性特点，找到一个周期变化情况，分析整个过程中有多少个周期再余多少次，就可分析得知.跨学科的图形变化问题，关键是按其它学科的规律画图或总结规律，分析综合数学知识与方法，就会使问题得以解决.

参考文献：

[1]葛培福.动态问题中扇形面积求解策略分析[J].数理化学习（初中版），2017（05）：20-21.

[2] 徐中华.“阴影面积问题”求解策略 [J].中学数学，2008（18）：34-36.

（收稿日期：2019-08-08）