2种经典模型对抗生素与重金属锌的蛋白核小球藻时间依赖联合毒性作用的评估比较
王滔,张瑾,卞志强,姜慧,申慧彦
安徽建筑大学环境与能源工程学院,安徽省水污染控制与废水资源化重点实验室,合肥 230601
抗生素通常用于治疗和预防人类和动物的致命感染[1],但抗生素不能完全被机体吸收,大约有20%~75%会通过粪便或代谢产物排出[2]。由于去除抗生素的水处理工艺尚不完善,城市污水处理厂成为向环境排放抗生素的主要源头[3]。进入水体的抗生素不仅污染环境,而且会对水生生物的生存甚至人类的健康构成潜在的威胁。据文献报道,环境中有的抗生素具有较强的生物毒性,有的抗生素残留会诱导出耐药细菌,甚至通过食物链的传递作用最终在人体内积累并产生危害[4-6]。氨基糖苷类抗生素是一种价廉、高效的广谱性杀菌剂,对严重的细菌感染尤其有效,在世界范围内得到广泛使用,导致其在环境中的大量残留,引起了人们的普遍关注[7-8]。
重金属是环境中另一类典型的污染物,越来越受到全球尺度的特别关注[9]。重金属污染物通过各种自然和人为来源被引入水体环境,包括家庭排放以及采矿和冶炼等工业排放[10]。由于重金属是不可生物降解的持久性污染物,容易在生物体中积累,对生态系统甚至人类健康构成威胁[11],如重金属锌,因其在日常生产和生活中的广泛应用而进入水体环境中,成为环境污染物,水生生物对其具有很强的吸附能力,且容易在生物体内富集,当浓度过高时会造成生物组织氧化损伤[12]。然而,污染物在环境中不是以单个物质的形式存在,而是以各种形式和浓度共存,不同组分间可能产生累积与联合毒性作用,且随着暴露时间的延长,其潜在的环境风险可能会更大[13]。目前有很多关于重金属或抗生素单一污染物对生物毒性效应的研究,但很少有两者联合毒性作用动态变化规律的研究[14]。
关于污染物联合毒性作用,早期使用的评估方法主要包括等效线图法、混合毒性指数法和相似性参数法等[15-16]。这些传统方法多采用等毒性浓度设计混合物,考察浓度范围单一,具有较大局限性。在2000年时,德国不来梅大学的学者利用非线性函数模拟剂量-效应曲线,用回归方法计算低效应浓度,并将浓度加和(concentration addtion, CA)与独立作用(independent action, IA)模型应用于多元混合物浓度-效应的预测[17],此后污染物联合毒性相互作用的研究进入了新时期。CA和IA模型应用也越来越广泛,一般情况下,CA模型适用于具有相似毒作用模式/作用机制(mode/mechanism of toxic action, MOA)污染物的混合物毒性评估,而IA模型适用于具有相异MOA污染物的混合物毒性评估[18]。但对于大多数污染物,其生物毒性作用机理不是完全清楚,越来越多的学者在进行混合物毒性评估时,同时使用2种模型,然后选择较合适的模型。也有学者只采用其中一种模型(CA模型更为常用)评估混合毒性作用。然而,文献中同时将2种模型CA和IA用于评估具有时间依赖特征的污染物间联合毒性作用的研究较少[19-20]。
鉴于此,本研究拟以3种氨基糖苷类抗生素和重金属锌为研究对象,以蛋白核小球藻为测试生物,采用直接均分射线法[21]设计抗生素和重金属不同浓度配比的代表性混合物,应用时间毒性微板分析法[22]系统测定单个污染物及其混合物在不同暴露时间的毒性,应用CA与IA模型评估在不同暴露时间的混合物毒性相互作用,揭示抗生素和重金属混合污染物毒性相互作用随时间变化规律,并比较2种模型预测结果的异同,以期为科学评价抗生素与重金属混合物的环境风险提供数据和方法参考。
1 材料与方法(Materials and methods)
1.1 材料
3种氨基糖苷类抗生素包括硫酸安普霉素(apramycin sulfate, APR)、双氢链霉素(dihydrostreptomycin sulfate, DIH)和硫酸链霉素(streptomycin sulfate, STS),均购自上海原叶生物科技有限公司,其理化性质列于表1中。重金属选择氯化锌化合物,购自国药集团化学试剂有限公司,其理化性质列于表1中。测试药品储备液用超纯水配制,并于4 ℃冰箱中保存、备用。
Synergy 2 Multi-Mode多功能酶标仪(美国BioTek伯腾仪器有限公司),YXQ-LS-100S11立式压力蒸汽灭菌器(上海博讯医疗生物仪器股份有限公司),MGC-250智能型光照培养箱(上海一恒科学仪器有限公司)。
1.2 藻种与培养
实验藻种:蛋白核小球藻(C. pyrenoidosa)购自中国科学院典型培养物保藏委员会淡水藻种库(FACHB),编号为FACHB-5。C. pyrenoidosa的培养基成分及培养过程见参考文献[23]。
1.3 时间毒性测定与数据拟合
微板设计与时间毒性的测定方法见参考文献[23],污染物及其混合物对蛋白核小球藻在不同暴露时间的生长抑制率按如下公式进行计算[23]:
Ei,j=(1-μi,j/μ0,j)×100%
(1)
式中:Ei,j为污染物在暴露时间j(j = 12, 24, 48,72, 96 h)对C. pyrenoidosa的生长抑制率;μi,j为ci微孔中C. pyrenoidosa在暴露时间j时的平均生长速率;μ0,j为微板中空白藻在暴露时间j时的平均生长速率[24]。
对各个污染物及其混合物在不同暴露时间的浓度-抑制率数据进行非线性拟合的两参数函数Logit公式[23]:
E=1/[1+exp(-α-β×lgc)]
(2)
式中:E表示效应;c表示单个化合物或混合物的浓度;α和β分别为位置和斜率参数。
1.4 混合物实验设计
为系统考察二元混合物毒性随时间和浓度的变化规律,采用直接均分射线法(Equ-Ray)设计3个二元混合物体系,每个体系有5条浓度比不同的射线[25],每条混合物射线的组分及其浓度比(pi)列于表2中。

表1 3种抗生素与重金属锌的理化性质Table 1 Physiochemical properties of three antibiotics and one heavy metal Zn
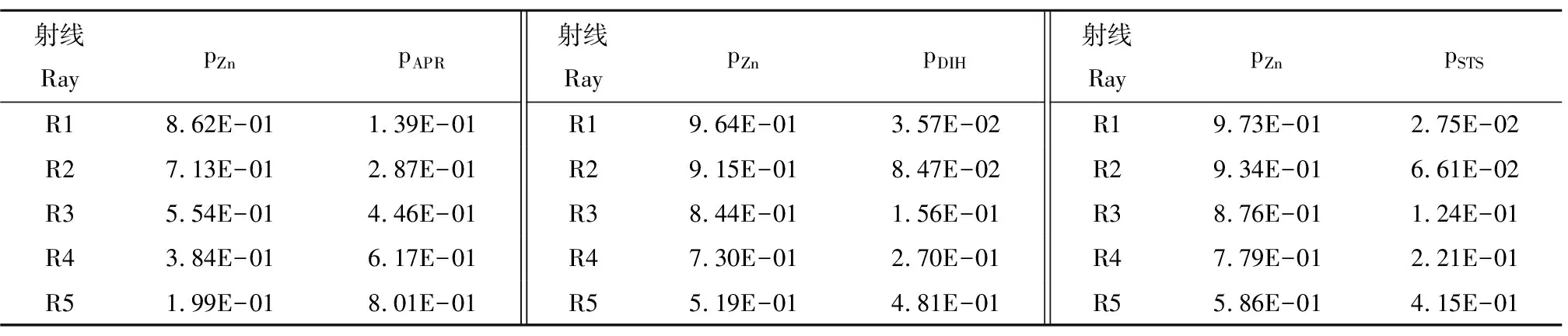
表2 3组二元混合物体系的组分及其浓度比(pi)Table 2 The components and their concentration ratios (pi) of three binary mixture systems
1.5 混合物毒性相互作用分析
CA和IA模型是混合物毒性评估中常用的加和参考模型,计算公式见(3)和(4)[26-28],如果混合物的观测毒性等于、大于或小于预测毒性,则混合物毒性相互作用分别为加和作用、协同作用或拮抗作用。
CA模型数学表达式为:
(3)
IA模型数学表达式为:
(4)
式中:ci表示混合物中产生某一效应x%时组分i的浓度,ECx,i表示混合物中第i个化合物单独存在时产生效应x%时的浓度。
2 结果与讨论(Results and discussion)
2.1 抗生素和重金属锌对C. pyrenoidosa的时间毒性
Logit非线性函数能较好拟合污染物及其混合物对C. pyrenoidosa的浓度-效应数据[29]。应用t-MTA方法测定不同暴露时间时浓度-效应数据,并将拟合的浓度-效应曲线(CRC)绘于图1。从图1可以看出,3种抗生素对C. pyrenoidosa的毒性具有明显的时间依赖性,即在开始的12 h,3种抗生素对C. pyrenoidosa基本无毒性,随着暴露时间延长,毒性逐渐增加,在72 h后增幅变缓。而锌对C. pyrenoidosa的时间依赖毒性不如抗生素明显,在12 h就达到50%以上的抑制率。

图1 3种抗生素和Zn在不同暴露时间对蛋白核小球藻的浓度-效应曲线Fig. 1 The concentration-effect curves of three antibiotics and Zn in different time toward C. pyrenoidosa
为了比较抗生素对C. pyrenoidosa在不同暴露时间的毒性大小(通常以半数效应浓度的负对数pEC50表示),以时间为X轴,pEC50为Y轴作图,4种物质在0~96 h内的pEC50值变化曲线如图2所示。从图2可以更明显地看出4种物质pEC50值随暴露时间的延长而增大,但不同物质的pEC50值随时间变化的规律稍有不同,如Zn的pEC50值随时间的延长,在缓慢增加,而抗生素APR和STS在0~48 h内抑制率低于50%,但48 h后pEC50值迅速增加,然后增速减慢。抗生素DIH在0~72 h也达不到50%的抑制率,在72 h后pEC50值迅速增加,甚至超过APR和Zn的pEC50值。可见,4种物质的毒性随暴露时间的变化而发生变化,但不同物质变化的规律不同。以pEC50值为毒性大小的判断依据,则在暴露时间节点12 h和24 h,只有Zn有毒性,pEC50值分别为2.503和2.706;在暴露时间节点48 h,除抗生素DIH没有毒性,其他都呈现出一定的毒性,其毒性大小顺序为:STS>APR>Zn;在暴露时间72 h和96 h,4种污染物毒性大小顺序均为:STS>DIH>APR>Zn。结果表明,暴露时间也是污染物的生物毒性的重要影响因素,因此,只有系统考察浓度与时间2个因素,才能比较客观和全面地了解污染物的生物毒性效应,才能更深入地了解污染物的毒理作用机制与途径,提高生态风险评估的可靠性。
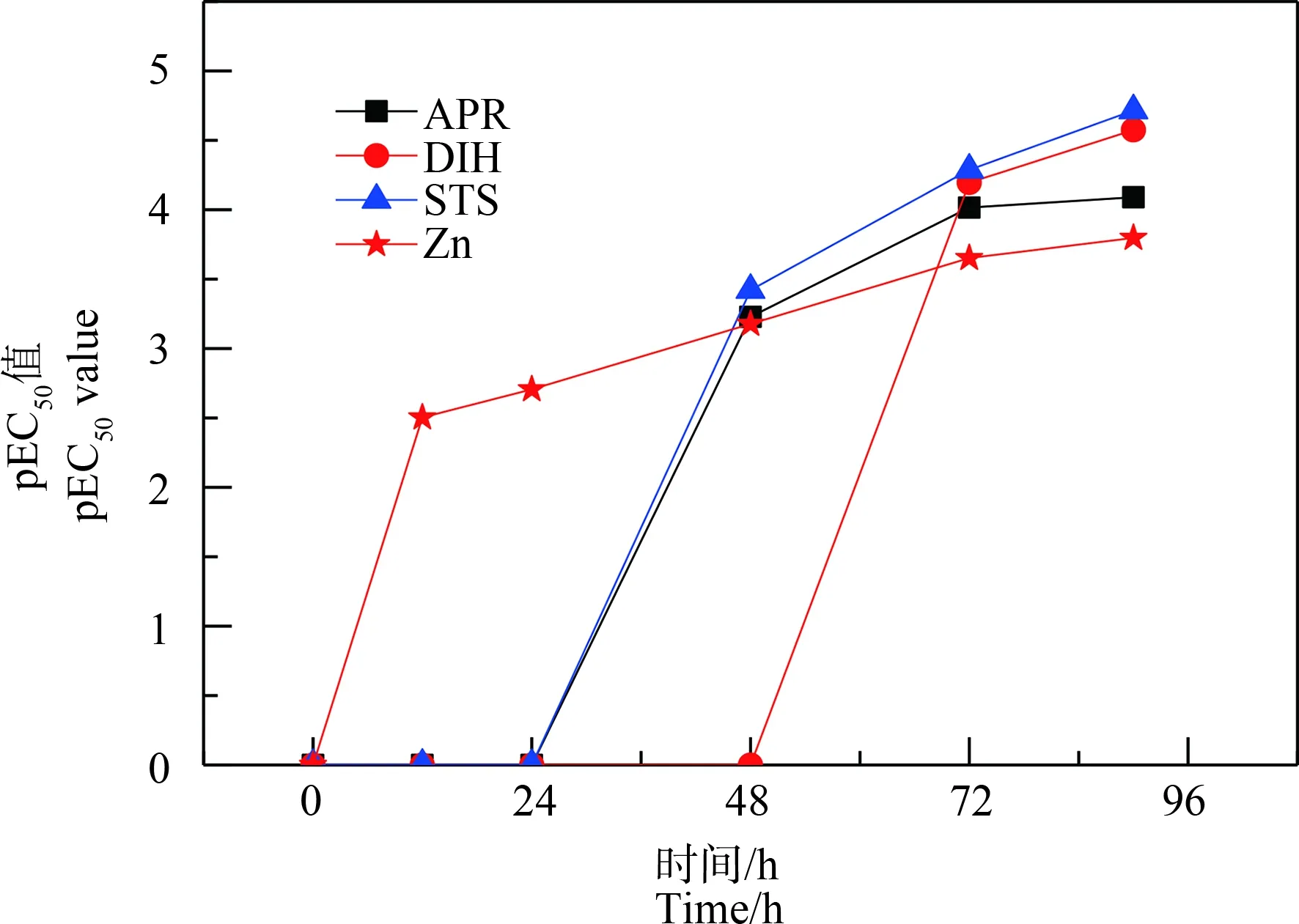
图2 3种抗生素和Zn的pEC50值随时间变化曲线Fig. 2 The changing curves of pEC50 values of three antibiotics and Zn with time
2.2 抗生素-重金属锌的二元混合物对C. pyrenoidosa的时间毒性
抗生素与重金属二元混合物对蛋白核小球藻的浓度-效应数据点及其拟合结果如图3所示。从图3可看出,3个混合物体系中的每条混合物射线对C. pyrenoidosa也具有明显的时间依赖毒性。结合表2,可看出抗生素与锌二元混合物体系的射线R1到R5,Zn的浓度比逐渐减小,抗生素的浓度比逐渐增加,混合物体系中射线的毒性随时间的依赖性也逐渐明晰,这可能是由于抗生素对蛋白核小球藻具有明显的时间依赖毒性。
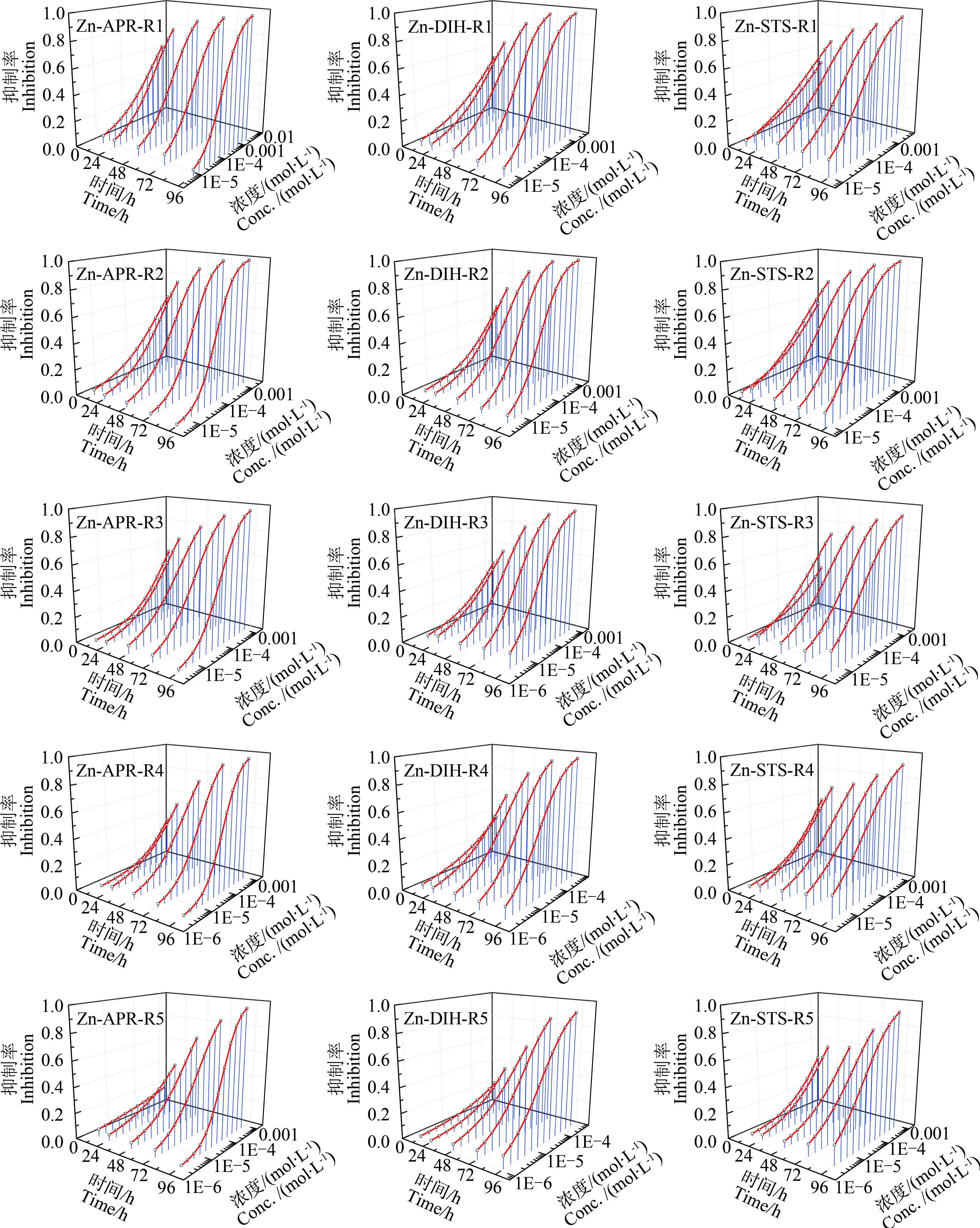
图3 3个混合物体系在不同暴露时间对蛋白核小球藻的浓度-效应曲线Fig. 3 The concentration-effect curves of three mixture systems in different time toward C. pyrenoidosa
图4是3组混合物体系中各射线的pEC50值随时间的变化图。从图4可知,各组混合物射线的pEC50值随暴露时间的延长逐渐增加,但具有不同浓度比射线的pEC50值随时间变化的规律稍有不同,如在Zn-APR混合物体系中,射线R1、R2和R3在暴露时间12 h就达到50%的抑制效应,pEC50值从暴露时间12 h开始,随时间的延长而逐渐增加,72 h后不再增加,而R4和R5则在48 h之后才达到50%的抑制效应,然后随时间延长逐渐增加;在Zn-DIH混合物体系中,射线R1和R2在暴露时间12 h就达到50%的抑制率,随时间的延长而逐渐增加,96 h后不再增加,R3和R4则在24 h之后才达到50%的抑制效应,然后随时间延长逐渐增加,R5则在48 h之后才达到50%的抑制效应;在Zn-STS混合物体系中,射线R1和R2的pEC50值从暴露时间12 h就开始随时间的延长而逐渐增加,而R3、R4和R5则在24 h之后才达到50%的抑制效应,然后随时间延长逐渐增加。对于Zn-DIH和Zn-STS这2个混合物体系,在96 h时各条射线的毒性大小顺序均为R5>R4>R3>R2>R1,结合表2可知,混合物毒性随组分中抗生素浓度比的增加而增加,具有明显的组分浓度比依赖毒性,Zhang等[30]也发现了混合污染物毒性与其组分的浓度配比有关。
2.3 抗生素与重金属锌之间的时间依赖毒性相互作用
应用CA和IA模型对Zn-APR、Zn-DIH和Zn-STS这3组混合物体系的15条射线进行毒性相互作用分析,结果见图5。由于3个混合物体系的射线中,有的呈现协同作用,有的呈加和作用,但3个混合物体系中的5条射线的协同作用随暴露时间延长的变化规律相似,因此,图5给出3个混合物体系中各自具有代表性的混合物射线的实验观测值及其95%置信区间(observed confident interval, OCI)、拟合曲线以及CA和IA预测结果。
从图5可以看出,部分射线的CA和IA预测曲线位于实验观测置信区间下方,表现为协同作用,其余射线的CA和IA预测曲线位于实验观测置信区间内,表现为加和作用。但在不同混合物体系中,毒性相互作用发生的浓度区域不同,如Zn-APR和Zn-DIH混合物体系中协同作用主要发生在较高浓度区域,而Zn-STS混合物体系中加和作用发生在整个浓度区域,这表明毒性相互作用类型与混合物的浓度有关。
图5还显示,混合物体系在不同暴露时间的协同作用强度不同,Zn-APR和Zn-DIH这2个混合物体系具有相似的规律。在12 h到24 h期间,随着暴露时间延长,协同作用逐渐增强。在24 h到48 h期间,协同作用逐渐减弱,48 h后逐渐向加和作用转变。

图4 3个混合物体系的pEC50值随时间变化图Fig. 4 The changing of pEC50 values with the time for three mixture systems

图5 3个Zn-抗生素混合物体系代表性射线的实验观测点及其95%置信区间、拟合浓度-效应曲线(CRC)以及CA和IA预测曲线注:图中分散点(·)表示实验点,实线(—)为拟合线,红色短断线(---)为CA预测曲线,黑色虚点点线(--)为IA预测曲线,蓝色虚点线(--)为95%置信区间。Fig. 5 The observed concentration-effect data with 95% confidential intervals, fitted concentration response curve (CRC) and predicted curve by CA and IA of representative ray of three Zn-antibiotics mixture systemsNote: black dispersed point (·), solid line (—), red short dash line (---), black dash dot dot line (--), blue dash dot line (--) refer to the observed data, the fitted line, predicted curve by CA, predicted curve by IA and 95% confidential interval.
这表明协同作用强度随暴露时间的变化而变化,即与暴露时间有关。
综上所述,3组抗生素和重金属的二元混合物体系对蛋白核小球藻的毒性具有明显的浓度和时间依赖性,因此,在进行污染物生态毒性评估时,需要考虑时间和浓度2个因素,才能深入了解组分间相互作用机制,从而更准确地评估生态风险。
2.4 2种经典模型对联合毒性的评估比较
通过比较CA和IA预测线与实验观测值之间的位置关系,并分析混合物体系在不同暴露时间和不同浓度区域的毒性相互作用,发现Zn-APR与Zn-DIH二元混合物体系的毒性相互作用变化具有相似的规律。在低浓度区域,CA和IA预测线始终位于实验观测OCI内,呈现出加和作用。在中浓度和高浓度区域内,CA和IA预测曲线在开始暴露的时候位于实验OCI下方,并随暴露时间延长逐渐向实验OCI靠近,96 h的CA预测线在高浓度区域时位于实验OCI下方,中浓度区域时位于实验OCI内,而IA预测线整体位于OCI内;这2个混合物体系使用CA与IA模型可以得到不同的结果,比较IA预测线与观测值的拟合CRCs,可知毒性相互作用从协同作用逐渐转变为加和作用,而比较CA预测线与观测值的拟合CRCs,可知中浓度区域的毒性相互作用始终呈现协同作用,高浓度区域的毒性相互作用从协同作用逐渐转变为加和作用。对于Zn-STS二元混合物体系,在24 h,中浓度区域的CA和IA预测曲线同时位于实验OCI下方,呈现出协同作用;而在其他时间和浓度区域内,预测线均位于实验OCI内,呈现出加和作用。以上结果表明2种模型对抗生素和重金属的二元混合物毒性评估结果除在少数射线的高浓度区域呈现出不同的作用类型外,基本一致。
综上所述,在不同混合物体系的不同射线中,CA与IA预测线之间的位置关系始终保持一致,即在总效应为10%以下时,CA与IA预测曲线几乎重合,但随着总浓度增加,CA与IA预测曲线的差距逐渐增大;当总浓度较高时,IA预测曲线始终位于CA预测曲线上方,这可能由于抗生素与重金属具有不同的MOA,而IA模型更适用于相异MOA污染物的混合物毒性评估,从而与实验观测值更加接近。这与宋晓青等[17]在部分除草剂与重金属混合体系对发光菌的毒性研究中的结论相似。也有学者认为当混合物组分的CRC较陡(steep concentration response curves),CA预测混合物毒性高于IA;当混合物组分的CRC较平(flat concentration response curves),CA预测混合物毒性低于IA,而本研究中2种物质的CRC曲线较平缓,但平缓和较陡CRC的界定不明确,尚需进一步深入研究。
本研究得出:
(1) 3种抗生素和重金属锌对蛋白核小球藻的毒性随暴露时间的延长而增强,有明显的时间依赖性,在暴露时间72 h后,4种物质的毒性大小顺序为STS>DIH>APR>Zn。
(2) 3组抗生素和重金属锌的二元混合物体系,对蛋白核小球藻的毒性相互作用,在低浓度区域始终呈现加和作用,而在高浓度区域则随暴露时间延长从协同作用逐渐转变为加和作用,具有明显的时间依赖毒性和浓度依赖毒性。
(3) CA与IA模型对3种抗生素和重金属Zn的混合物毒性作用评估结果,除少数射线的高浓度区域的作用类型不同外,基本一致,但随着总浓度增加,CA与IA模型之间预测值的差别逐渐增大,IA预测CRC曲线始终位于CA预测CRC曲线上方,更接近实验观测曲线,显示IA模型更适用于相异MOA污染物的混合物毒性评估。

