萤火虫算法参数分析与优化*

卓宏明，陈倩清

(浙江国际海运职业技术学院 船舶工程学院，浙江 舟山 316021)

0 引言

萤火虫算法Firefly Algorithm(FA)是2008年YANG X S[1-2]提出的一种新型群智能优化算法，其操作简单、参数少、易实现，成为众多学者研究的热点，在诸多领域得到了较好的应用[3-6]。然而决定算法性能的参数选择还缺少相关的深入研究，算法的参数设定对求解性能影响很大，因此，萤火虫算法的参数优化已成为急需解决的问题。

1 萤火虫算法及数学模型

萤火虫算法基本思想是模拟萤火虫的发光特性在一定区域内寻找伙伴，向位置较优的萤火虫移动，以达到寻优的目的。将问题的目标函数定义为萤火虫所处位置的适应度值，将优化过程模拟成萤火虫个体的相互吸引而引发的位置更新的过程，将个体的优胜劣汰过程类比为搜索和优化过程中用好的可行解取代较差可行解的迭代过程。

萤火虫算法的寻优主要由荧光亮度和吸引度两个关键要素实现。主要公式包括相对相对萤光亮度公式、相对吸引度公式和位置更新公式[1-2]，如下所示：

萤火虫的相对萤光亮度为：

I=I0×e-γrij

(1)

其中，I0为初始光强度，即在光源(r=0)处的光强度，与目标函数值相关，目标函数值越优自身亮度越高；γ为光强吸收系数即吸收因子，以体现光强的减弱特性，一般情况下γ∈[0.01，100]；r通常为萤火虫i与j间的欧氏距离。

萤火虫的吸引度为：

(2)

其中，β0为最大吸引力，即光源(r=0)处的吸引力。

萤火虫i被萤火虫j吸引而向其移动的位置更新公式如下：

xj(t+1)=xj(t)+βij(rij)[xi(t)-xj(t)]+αεj

(3)

其中，t为算法迭代次数；α为随机步长，一般取值范围为[0，1]；εj通常是由高斯分布、均匀分布或其他分布生成的随机数向量。

2 算法参数分析及数值试验

根据萤火虫算的数学模型可知萤火虫算法的需要设定的参数有：萤火虫数量n,步长因子α,光吸收因子γ，最大吸引度β0,最大迭代次数T，共5个参数。而对于大多数的应用问题，β0可取为1，通过单因素数值试验测试经典测试函数[7-8](见表1)分析萤火虫算法其他4个参数对算法性能的影响。

表1 测试函数[7-8]

算法参数的经验设置见表2，在进行单因素试验时固定三个参数，改变一个参数进行仿真试验。试验环境为Windows 7，64位操作系统，Core i5-4210U处理器，8 GB内存，MATLAB 7.11版本。为降低随机误差，每个测试函数每组参数组合分别独立运行20次。

表2 算法参数经验设置

2.1 萤火虫数量(n)对算法的影响

根据经验值，设置萤火虫数量n=10、20、30、…、90、100。对3个测试函数进行独立运行20次的数值试验。试验结果见表3，对应各测试函数的平均最优解曲线如图1所示。

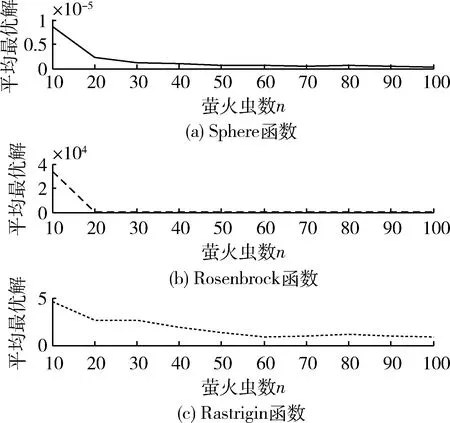
图1萤火虫数n对算法性能的影响

从理论定性地来看，萤火虫数越多找到最优解的可能性越大，算法的求解精度也越高，但也会产生大量重复解。从表3及图1分析可以发现共性的规律：随着萤火虫数n的增多，对应的平均最优解也越精确，越趋于平缓，这与理论定性分析相吻合。但各测试函数又有其各自的特点。

Sphere函数的求解精度很高，并且最优解与最差解差距也较小，具有较好的鲁棒性。但当萤火虫数n超过50时，求解精度已经基本稳定，过多的萤火虫数反而会增加计算开销，浪费资源。根据图表综合考虑求解精度及计算开销，对于Sphere函数，萤火虫数n取50时较为合理。

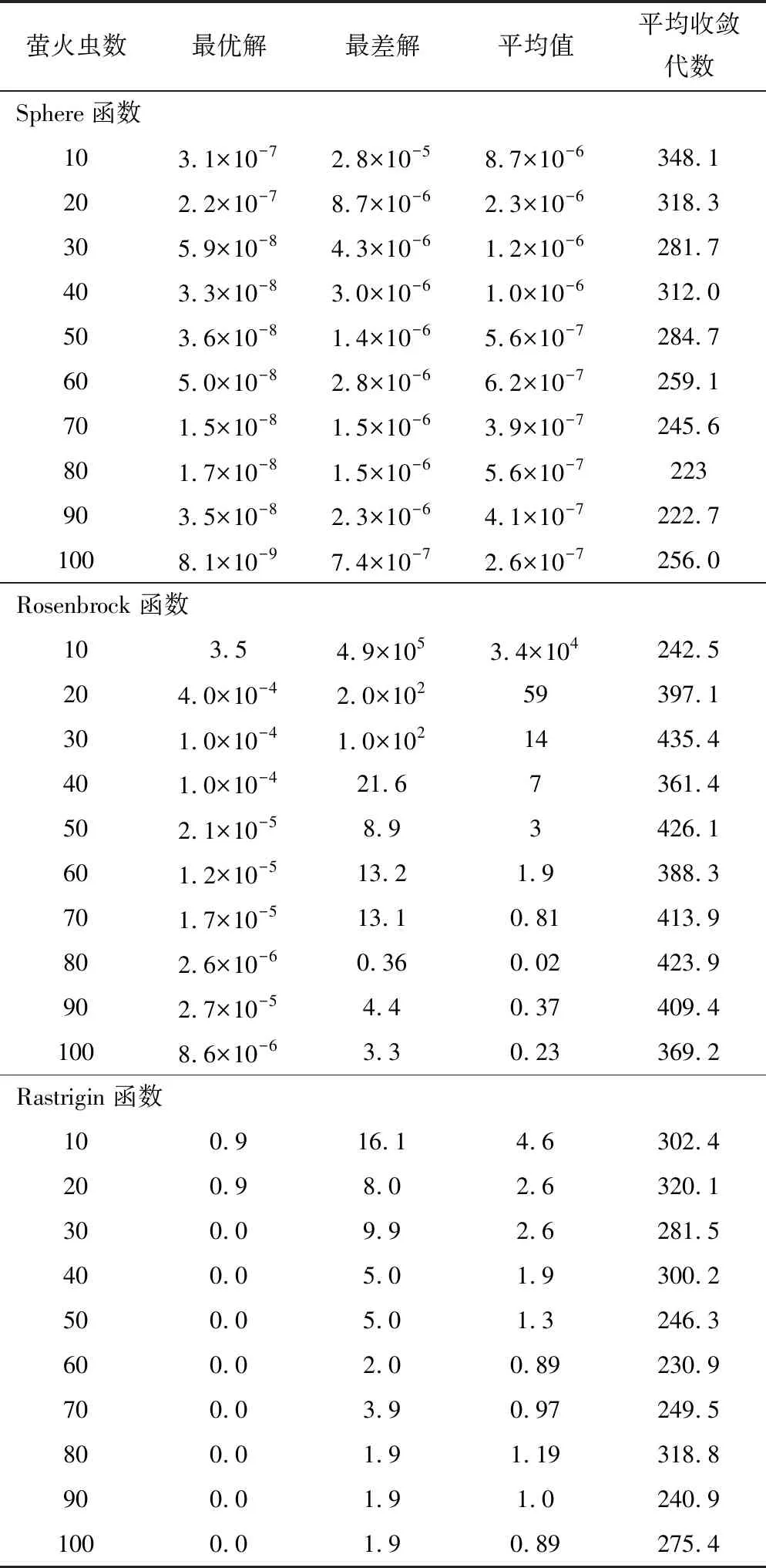
表3 萤火虫数n对算法性能的影响

Rosenbrock函数由于其复杂性，萤火虫算法对其求解精度不是非常高，并且最优解与最差解差距也较大。根据图表综合考虑求解精度及计算开销对于Rosenbrock函数，萤火虫数n取70时较为合理。

Rastrigin函数由于其易陷入局部最优，萤火虫算法对其求解精度也不是非常高，最优解与最差解差距一般。根据图表综合考虑求解精度及计算开销对于Rastrigin函数，萤火虫数n取60时较为合理。

2.2 步长因子(α)对算法的影响

根据常用步长因子取值区间α= [0,1],设置步长因子α=0.1、0.2、0.3、…、0.9、1。对3个测试函数进行独立运行20次的数值试验。试验结果见表4，对应各测试函数的平均最优解曲线如图2所示。

表4 步长因子α对算法性能的影响

图2 步长因子α对算法性能的影响

从理论角度定性地来看，步长因子α直接影响萤火虫寻优移动的步长，步长越小求解越精确，但容易陷入局部最优，步长越大收敛的速度越快，但会降低求解精度。从表4及图2分析可见步长因子的大小直接影响了算法的求解精度。各测试函数又有其各自的特点。

Sphere函数随着步长因子α的增加，算法的求解精度越差。但从整体来看平均求解精度在10-6和10-7，求解精度已经很高，并且最优解与最差解差距也较小，具有较好的鲁棒性。步长因子α越小精度越高，也越趋于平缓。根据图表所示，对于Sphere函数，步长因子α取0.1时较为合理。

Rosenbrock函数随着步长因子α的增加，算法的求解精度越高，也越趋于平缓。根据图表所示，对于Rosenbrock函数，步长因子α取1时较为合理。

Rastrigin函数随着步长因子α的增加，算法的求解精度越高，但有微小振荡。根据图表所示，对于Rastrigin函数，步长因子α取1时较为合理。

2.3 吸收因子(γ)对算法的影响

根据常用经验值γ=1及取值区间γ= [0.01,100],设置光强吸收因子γ=0.01、0.05、0.1、0.5、1、5、10、50、100。对3个测试函数进行独立运行20次的数值试验。试验结果见表5，对应各测试函数的平均最优解曲线如图3所示。

从算法数学模型理论定性地来看，吸收因子γ越小体现光强的减弱越小，从而使得萤火虫相对萤光亮度以及吸引度越大，越容易被位置优的萤火虫吸引，从而加速收敛。但也可能会降低随机扰动新解的开拓，反而降低求解精度。因此，需要合理设定吸收因子γ，以获得较高的求解精度及求解速度。从表5及图3分析可见其大小直接影响了算法的求解精度。各测试函数又有其各自的特点。

Sphere函数随着吸收因子γ的增加，算法的求解精度越差，但有微小振荡。从整体来看吸收因子在10及以下时，平均求解精度在10-6和10-7，求解精度已经很高，并且最优解与最差解差距也较小，具有较好的鲁棒性。根据图表所示，对于Sphere函数，吸收因子γ取0.5时较为合理。

Rosenbrock函数随着吸收因子γ的增加，算法的求解精度越差。根据图表所示，对于Rosenbrock函数，吸收因子γ取0.01时较为合理。

Rastrigin函数随着吸收因子γ的增加，算法的求解精度越高，但有微小振荡。根据图表所示，对于Rastrigin函数，吸收因子γ取50时较为合理。

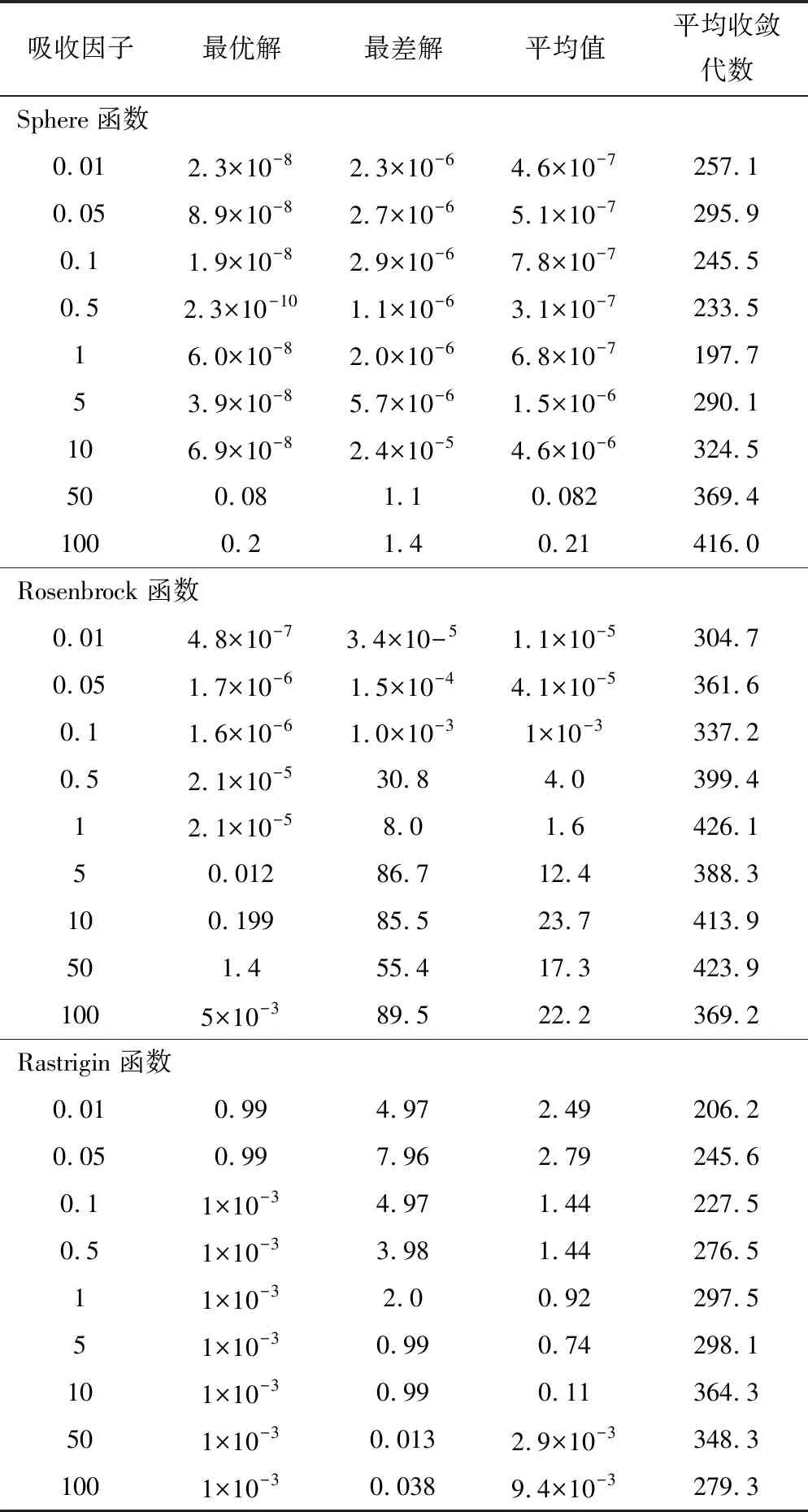
表5 吸收因子γ对算法性能的影响

图3 吸收因子γ对算法性能的影响

2.4 最大迭代次数(T)对算法的影响

根据经验值，最大迭代次数T=100、200、300、…、900、1 000。对3个测试函数进行独立运行20次的数值试验。试验结果见表6，对应各测试函数的平均最优解曲线如图4所示。

从理论定性地来看，最大迭代次数T越大找到最优解的可能性越大，算法的求解精度也越高，但会越趋于平缓，也会大量增加计算开销。从表6及图4分析可以发现：Sphere函数和Rosenbrock函数，随着最大迭代次数T的增多，对应的平均最优解也越精确，越趋于平缓，这与理论定性分析相吻合。但Rastrigin函数却处于小幅振荡中，各测试函数有其各自的特点。

Sphere函数的求解精度很高，并且最优解与最差解差距也较小，具有较好的鲁棒性。但当最大迭代次数T超过700时，求解精度已经基本稳定，过多的迭代反而会增加计算开销，浪费资源，根据图表综合考虑求解精度及计算开销，对于Sphere函数最大迭代次数T为700时较为合理。

Rosenbrock函数由于其复杂性，萤火虫算法对其求解精度比Sphere函数低的多，并且最优解与最差解差距也较大。根据图表综合考虑求解精度及计算开销，对于Rosenbrock函数最大迭代次数T为700时较为合理。

Rastrigin函数由于其易陷入局部最优，萤火虫算法对其求解精度也不是非常高，最优解与最差解差距也较大。并且从图表中发现其处于小幅振荡，说明只增大最大迭代次数无法提高其求解精度，需要综合考虑其他各参数。综合考虑求解精度及计算开销，对于Rastrigin函数最大迭代次数T为700时较为合理。

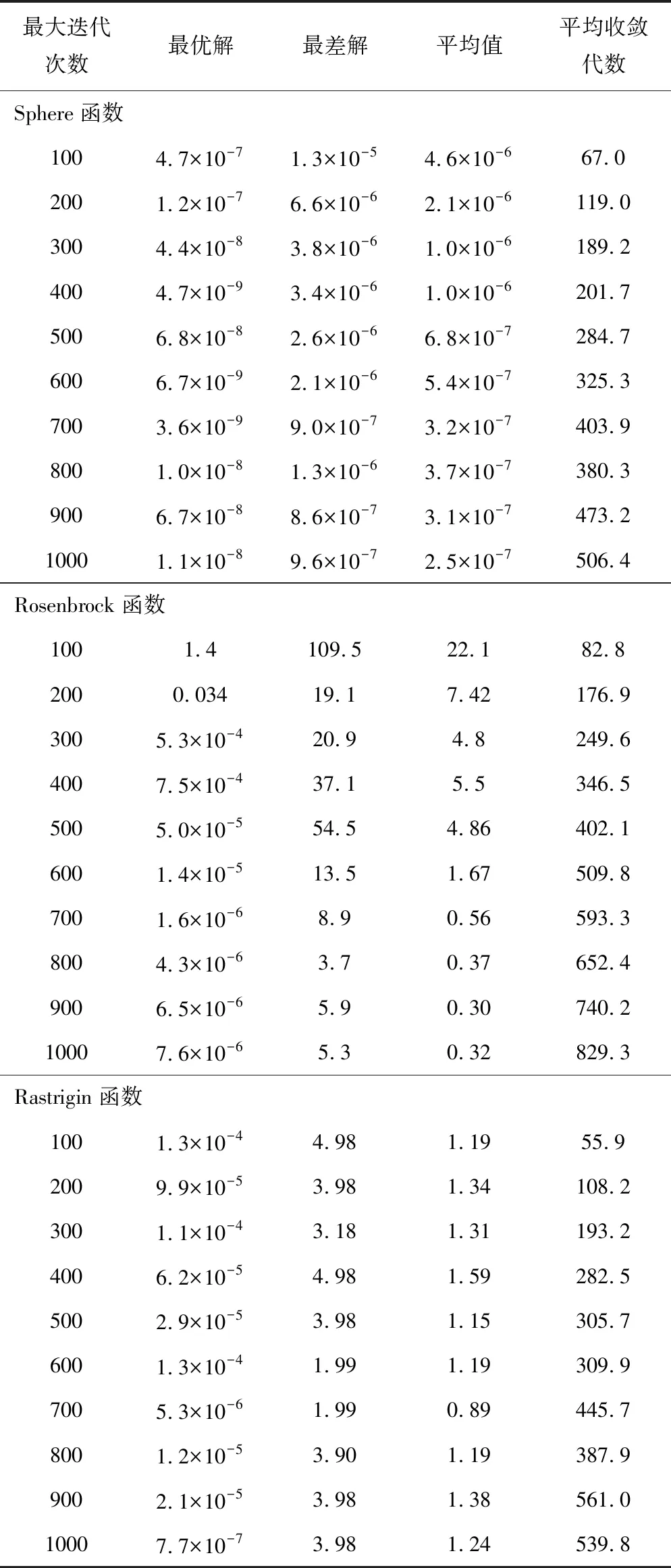
表6 最大迭代次数T对算法性能的影响

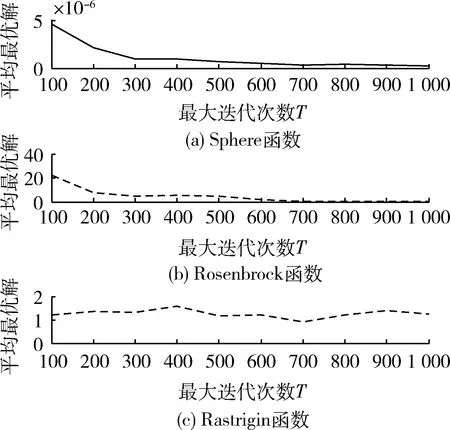
图4 最大迭代次数(T)对算法性能的影响

3 算法参数优化

根据前面的算法参数分析及对各测试函数的仿真试验结果整理各对应优化参数见表7。

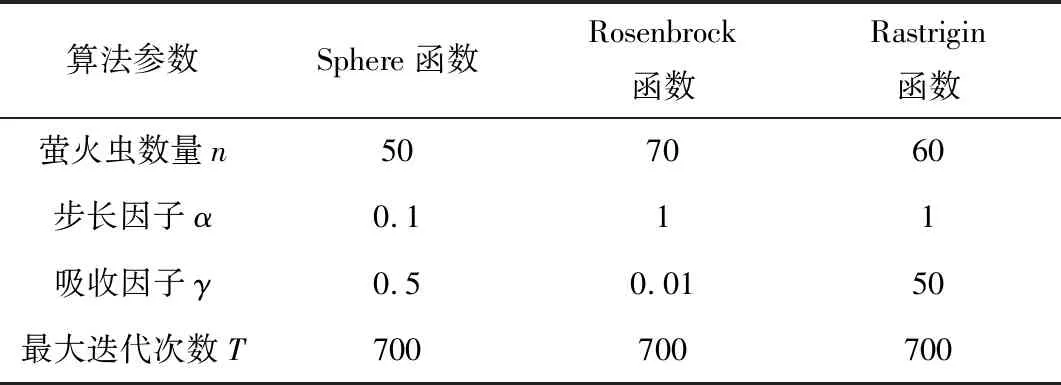
表7 算法参数优化设置

再根据优化前的经验参数与优化后的算法参数对各测试函数在相同测试环境下进行对比数值实验，各测试函数分别独立运行20次。试验结果对应各测试函数的平均最优解收敛曲线如图5、图6所示，对比结果见表8。

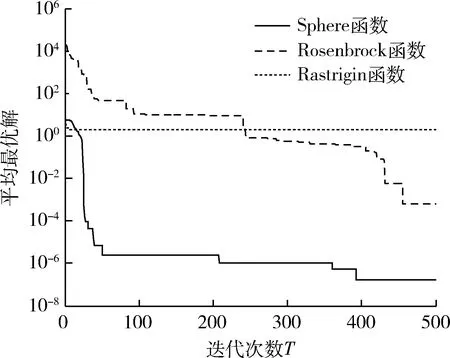
图5 参数优化前测试函数收敛曲线

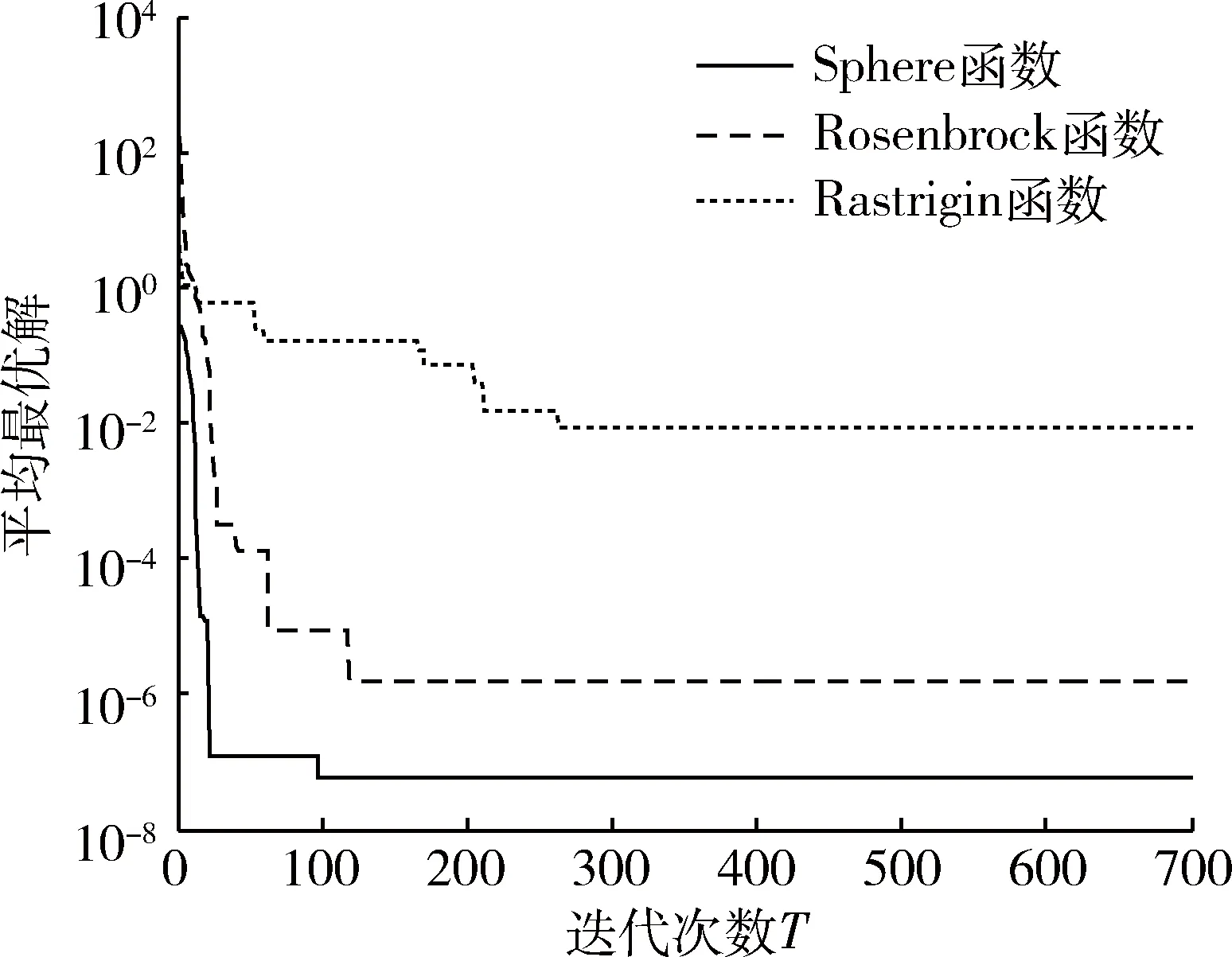
图6 参数优化后测试函数收敛曲线

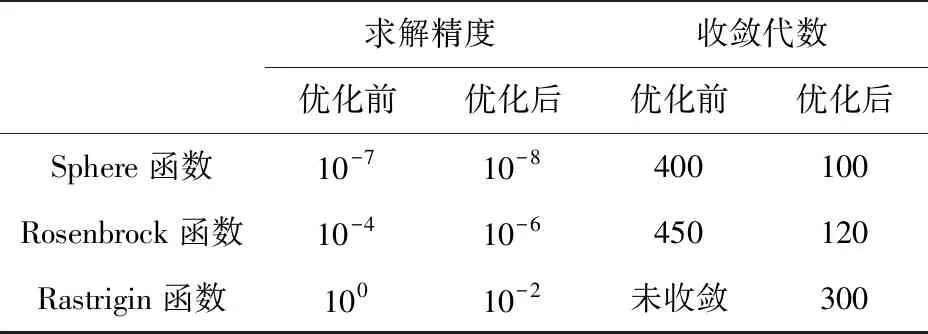
表8 算法参数优化前后对比效果

从图表中可见参数优化后的3个测试函数随着迭代次数的增加都明显收敛，求解精度提高了1～2个数量级，并且收敛代数也明显减少，提高了算法的求解精度和速度。

4 结论

(1)萤火虫数n越大，萤火虫算法的求解精度也越高，但越趋于平缓，也会产生大量重复解，增加计算开销。步长因子α越小求解越精确，但容易陷入局部最优，步长因子越大收敛的速度越快，但会降低求解精度。吸收因子γ越小越可加速收敛，但也可能会降低随机扰动新解的开拓，降低求解精度。最大迭代次数T越大找到最优解的可能性越大，算法的求解精度也越高，但会越趋于平缓，也会大量增加计算开销。

(2)合理设置参数可以充分发挥算法的寻优性能。萤火虫算法参数优化后比优化前对各测试函数的求解精度和速度都有了明显提高。求解精度提高了1～2个数量级，并且收敛代数也明显减少。

下一步将研究考虑各参数之间的相互影响及算法参数的动态调整，并应用于具体工程问题。