基于改进RNN的多变量时间序列缺失数据填充算法*

孙晓丽，郭 艳，李 宁，宋晓祥

(中国人民解放军陆军工程大学 通信工程学院，江苏 南京 210007)

0 引言

多元时间序列数据在医疗保健[1]、神经科学[2]、语音识别[3]、金融营销[4-5]、气象[6-7]、交通工程[8-9]等诸多应用领域都有丰富的应用。然而由于多种原因，如医疗事故、节约成本、异常现象以及设备故障等，这些多变量时间序列不可避免地会存在部分缺失数据。缺失数据的存在会影响数据分析的精度、正确的模型建立，甚至会带来灾难性的后果。因此，如何对缺失数据进行准确地填充已经成为大数据研究领域的一个热点。

缺失数据的填充是数据得以进一步开发利用的关键。目前，专家学者在各个领域进行了大量的研究工作，提出了许多有效的缺失数据填充算法[10]。处理时间序列数据中随机信息缺失的标准方法有插值法[11-12]和填充法[13-15]。其中，插值法试图通过利用单个序列中的时间关系来重建缺失数据。填充法则试图通过利用多个数据序列来填充缺失数据。文献[16]以静态数据为研究背景，将模型约束为线性模型来填充缺失数据。然而，这种方法不能捕捉非线性和时间序列的特性。除此之外，包括自回归移动平均模型(Autoregressive Integrated Moving Model,ARIMA)[17]、季节性差分自回归滑动平均模型(Seasonal ARIMA,SARIMA)[18]等在内的自回归方法旨在将时间序列中的非平稳部分进行剔除，拟合出参数化的平稳模型。基于矩阵分解的方法也经常[19]被用来解决缺失数据填充问题，但是通常只适用于静态数据，并且需要较强的假设。

递归神经网络(Recurrent Neural Network,RNN)具有很好的性能，如强大的预测能力以及捕获长期时间依赖关系和可变长度观察的能力。近年来，RNN，如LSTM[20]和门控递归单元(Gated Recurrent Unit,GRU)[21]，在时间序列或序列数据的许多应用中凸显了至关重要的地位。文献[22]提出了多向递归神经网络(Multi-directional Recurrent Neural Network,M-RNN)的方法，并利用双向RNN来进行数据填充，但是删除了缺失变量之间的关系，将M-RNN的输入值作为常数进行处理，在网络中得不到充分的更新。文献[23]将深度神经网络的思想与卡尔曼滤波器相结合，提出了一种非线性状态空间模型——深度卡尔曼滤波器。文献[24]引入随机递归神经网络(Stochastic Recurrent Neural Network,SRNN)，将RNN与状态空间模型相结合，形成随机序列神经生成模型。

为了更好地解决多元时间序列的缺失数据问题，本文提出了一种基于RNN的缺失数据填充算法。该算法通过利用RNN自身能够捕捉长期时间依赖关系以及预测能力的特性，在RNN的基础上引入了衰减机制，从而使得改进后的模型能够充分利用观测数据中的隐藏信息来提高数据填充的准确率。而后，通过对现有的观测数据进行学习，实现对缺失数据的填充，提高了数据填充的准确率。本文以上海空气质量数据集以及AReM数据集为实验数据，对所提算法进行检验。实验结果表明，与其他算法相比，在缺失率较低的情况下，所提算法的填充误差更小，填充效果更优。

1 缺失数据表示

假设一组含有N个变量、时间长度为T的多元时间序列数据X表示为：X={x1,x2,…,xT}T∈T×N，对于t∈{1,2,…,T}，xt表示为t时刻时所有变量的观测值，即N，那么则表示为t时刻第n个变量的观测值。设st为时间戳，即t时刻观测到数据的时间。

对于多元缺失数据，给定每个时刻每个变量的观测值一个缺失向量m∈{0,1}，并且有：

(1)

(2)

对缺失时间序列数据进行以上处理，可以在原数据集的基础上得到{X,M,Δ}，其中：

2 LSTM

长短时记忆(Long-Shokl-Term Memory,LSTM)网络[20]是RNN的一种，能够解决一般RNN存在的长期依赖问题，并且可以解决长序列训练过程中出现的梯度爆炸和梯度消失的问题，因而LSTM适用于处理、预测时间序列中时间间隔较长的问题。LSTM的结构如图1所示。

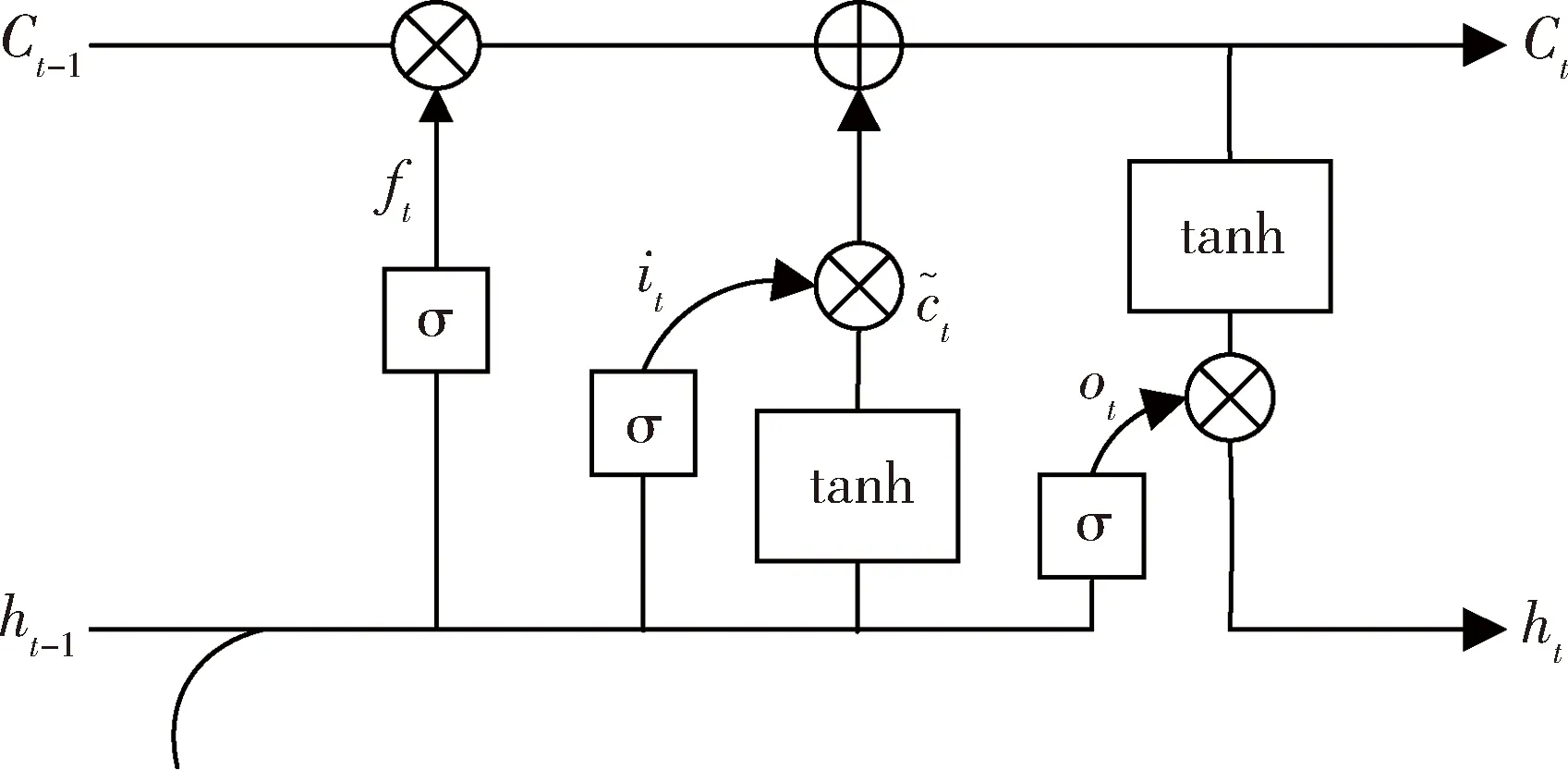
图1 LSTM结构图

一个经典的LSTM网络由单元或者记忆块组成，并且LSTM单元一般会有两个输出：单元状态C和隐藏状态h，将其传递到下一个LSTM单元，因此LSTM有三个输入：t-1时刻的单元状态Ct-1、隐藏状态ht-1以及t时刻的输入xt，有两个输出：t时刻的单元状态Ct、隐藏状态ht。记忆块通过三种门控制记忆隐藏状态和前面时刻发生的时间，三种门分别为：遗忘门、输入门和输出门。

LSTM的计算更新过程可以表示为：

it=σ(Wxixt+Whiht-1+bi)

(3)

ft=σ(Wxfxt+Whfht-1+bf)

(4)

(5)

(6)

ot=σ(Wxoxt+Whoht-1+bo)

(7)

ht=ot⊙tanh(Ct)

(8)

若此时的LSTM单元为网络中的最后一个单元，那么，网络最终的输出为：

y=softmax(W⊙ht+b)

(9)

其中，softmax为激活函数，W为权重矩阵，b为偏置矩阵。

3 提出的模型

3.1 γ-LSTM模型

结合时间序列中缺失数据的填充过程进行分析，会注意到，以往的RNN算法中，若缺失数据的丢失时间间隔过长，那么就导致缺失数据对当前时刻的输出影响随着时间间隔的增加而有所减弱。因此，本文在RNN的基础上引入了衰减机制，来捕获输入变量、隐藏变量与相应缺失数据时间间隔的关系，并且衰减系数γ的值因变量而异。改进后的RNN结构如图2所示，将其称之为γ-LSTM。

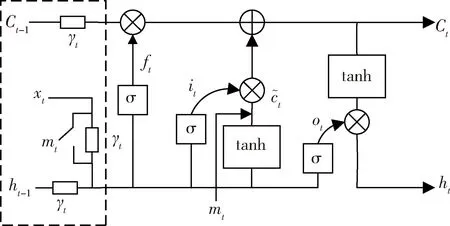
图2 γ-LSTM结构图

由图2可以看出，γ-LSTM在LSTM的基础上，使用时间衰减系数γt对LSTM单元的输入进行修正，并使用缺失向量mt对网络的中间结果进行一定的修正，使其更加充分地捕获数据间的相关关系，定义γt为：

γt=exp{-max (0,Wγδt+bγ)}

(10)

(11)

(12)

γ-LSTM对于输入的xt做了相应的处理，以其是否为缺失数据进行数值的确定，且有：

(13)

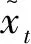
(14)

(15)

此时γ-LSTM的计算过程表示为：

(16)

(17)

(18)

(19)

(20)

ht=ot⊙tanh(Ct)

(21)

3.2 γ-PLSTM模型

由图1的结构图可以看出，t时刻LSTM门的输入包含两部分：网络输入与t-1时刻网络的输出，若在t时刻时输出门关闭(值接近0)，那么t时刻网络的输出将为0，t+1时刻LSTM网络的门将仅与网络的输入有关系，因此会导致历史信息的缺失，从而影响最终的结果。因此，文献[26]提出了一种LSTM的变体“猫眼”LSTM (Peephole LSTM,PLSTM)，其在LSTM的基础上增加了“猫眼”连接(图3中的虚线部分)，允许门查看细胞状态。PLSTM模型的计算过程如下：

图3 PLSTM结构图

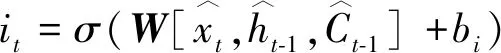
(22)

(23)

(24)

(25)

(26)

ht=ot⊙tanh (Ct)

(27)

LSTM中，单元状态C用于存储信息，有效地保持信息在多个时间步长中的清晰度；隐藏状态h用于上层输出，并且捕获单元状态中与当前时刻输出密切相关的部分。而PLSTM通过“猫眼”连接，即便是在信息匮乏的情况下，也可以生成精确的时间间隔事件。

为了更全面地解决缺失数据填充问题，考虑数据缺失时间间隔对当前时刻产生数据的影响，在PLSTM的基础上，同样引入衰减机制。引入衰减机制的PLSTM被称为γ-PLSTM，模型的结构如图4所示。

图4 γ-PLSTM结构图

对单元状态C以及隐藏状态h增加衰减处理，同样地，衰减系数γt定义如公式(10)，得到衰减处理后的结果见公式(11)、(12)。

对网络输入x作相同的处理，见公式(13)，此时模型的更新计算过程为：

(28)

(29)

(30)

(31)

(32)

ht=ot⊙tanh (Ct)

(33)

在缺失数据填充的模型中，在每个时间步长内都使用γ-PLSTM，并在其最后一个单元的输出后增加一个softmax层和dropout层，最终输出填充的缺失值。

4 数据集及评价方法

4.1 数据集

全国空气质量数据集来源于全国城市空气质量实时发布平台，记录了全国190个站点自2014年5月13日至2019年8月17日每天每个小时PM2.5、PM10、SO2、NO2、O3、CO含量以及分别对应的24小时均值与AQI实时值。从中选取上海三个月的空气质量数据作为仿真数据集进行实验。

AReM数据集来源于UCI数据库，该数据集数据是由无线传感器记录而来，实验者执行特定动作时被其身上所佩戴的传感器所记录，有6个属性，大约5万条数据记录，并且数据的分布具有一定的规律。从中选取1 000条记录作为仿真数据进行实验。

4.2 评价方法

为了更好地评价缺失值的填充效果，使用均方误差(Mean-Squared Error,MSE)、平均相对误差(Mean Relative Error,MRE)、均方根误差(Root Mean Squared Error,RMSE)来计算输出的缺失填充值与原数据之间的误差，定义如下：

(34)

(35)

(36)

5 仿真

本文选取上海空气质量数据以及AReM数据集作为实验数据，用以验证所提方法的有效性。实验中，首先对数据进行归一化处理，然后按照缺失率为10%、20%、30%、40%、50%从完整数据集中任意删除对应数量的数据。为了方便对数据进行处理，针对不同的变量，都随机删除相同数量的数据，每个变量的缺失率都与整个数据集的缺失率相同。

归一化过程表示为：

(37)

针对LSTM、γ-LSTM、PLSTM、γ-PLSTM模型，使用不同缺失率的上海空气质量数据、AReM数据进行检验，得到数据填充的效果如表1～表4所示。

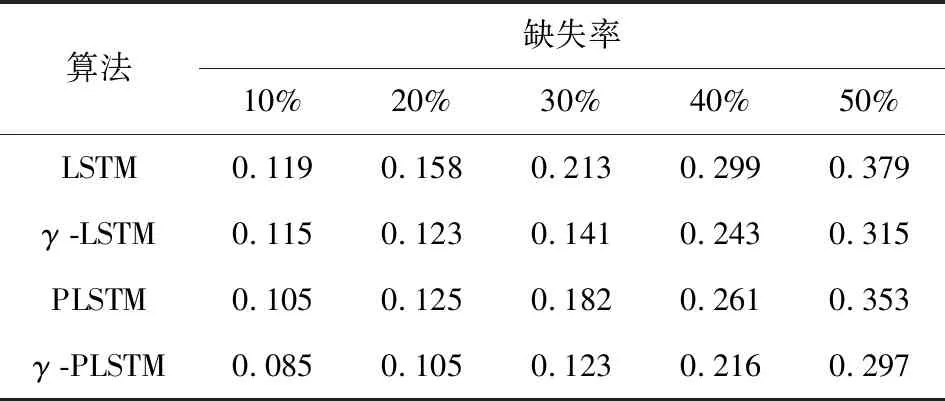
表1 空气质量数据集下四种算法的MSE(%)比较

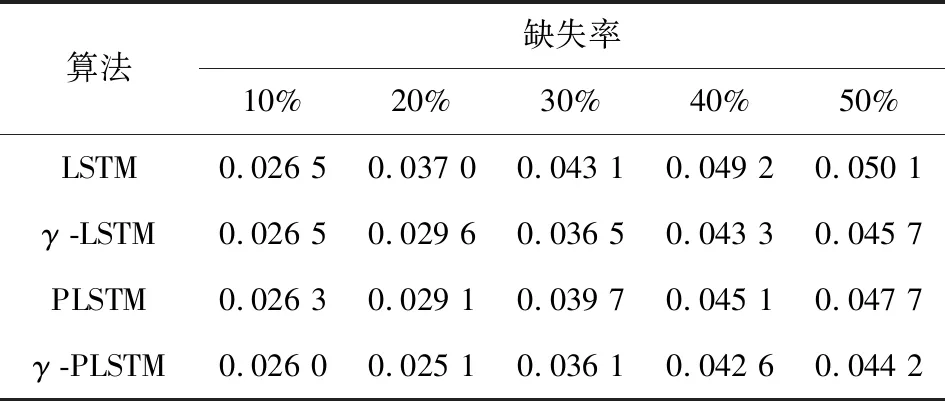
表2 空气质量数据集下四种算法的MRE比较

表3 AReM数据集下四种算法的MSE(%)比较

表4 AReM数据集下四种算法的MRE比较

由表1～表4可以看出，四种算法都可以实现对缺失数据的填充，随着缺失率的升高，填充数据的MSE、MRE误差都随之增大，偶尔出现波动，但并不影响大体规律。四种算法中，γ-PLSTM的填充效果较为显著，填充数据的MSE、MRE误差较其他三种小；在缺失率较低时，PLSTM的填充效果优于γ-LSTM，但随着缺失率的升高，γ-LSTM的效果则有明显改善且效果要优于PLSTM，也证明了衰减机制的作用；PLSTM、γ-PLSTM的效果分别比LSTM、γ-LSTM的效果好，很好地说明了在学习的过程中，对单元状态进行监控，能够更多更好地获得历史信息，从而更好地实现对缺失数据的填充。

对所提算法与现有算法(稀疏贝叶斯学习(Sparse Bayesian Learning，SBL)、RNN)进行对比实验，实验结果如图5、图6所示。

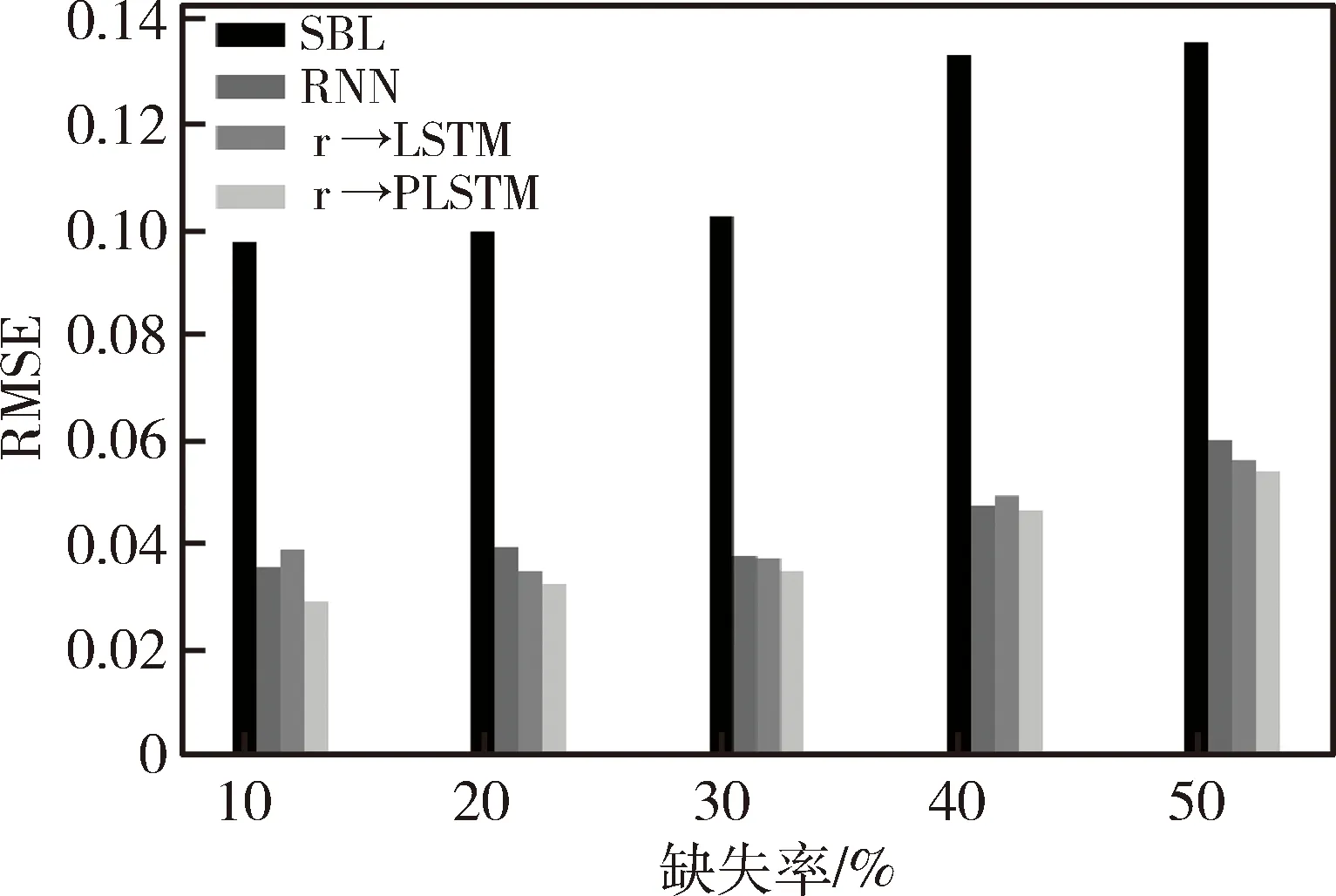
图5 空气质量数据下不同算法填充效果比较

图6 AReM数据下不同算法填充效果比较

通过图5、图6可以看出，四种算法都可以实现缺失数据的填充，但是填充的效果不尽相同。由实验结果可以看出，相对于其他三种算法而言，SBL算法适合处理精度要求不严格的缺失数据，RNN算法的填充效果相较于SBL而言更优，而本文所提的γ-LSTM和γ-PLSTM算法则较RNN而言填充效果更好。不难看出，伴随着缺失率的升高，四种算法的填充误差有所增加，且SBL的误差最大，γ-PLSTM的填充误差最小；整体而言，γ-LSTM的填充效果要优于RNN。

总体而言，通过SBL、RNN、γ-LSTM、γ-PLSTM四种算法的比较，可以清晰地发现所提两种算法γ-LSTM、γ-PLSTM在缺失数据填充中的优越性；通过LSTM、PLSTM与本文所提两种算法的比较，体现出增加衰减机制的作用以及在缺失率相对较高情况下“猫眼”连接与衰减机制共同作用的有效性。

6 结论

本文提出了一种基于LSTM的缺失数据填充算法来解决多变量时间序列的缺失数据填充问题。在LSTM的基础上引入了衰减机制，通过学习时间间隔与网络变量的关系，获取更多隐藏的历史信息，从而更好地完成缺失数据的填充；并对两种不同的传统LSTM进行改进，从而得到了两种不同的算法γ-LSTM和γ-PLSTM，通过实验比较，γ-PLSTM的性能要优于γ-LSTM，说明在缺失数据填充过程中，有“猫眼”连接的能够查看细胞状态的算法能够获得更多的隐藏信息，从而缺失数据的填充效果更为优异。