基于L2,P稀疏子空间和局部结构保持降维
庄姗姗
(福州大学 数学与计算机科学学院,福建 福州 350108)
0 引言
目前,高维数据已广泛存在于实际应用中,如生物工程、信息检索和计算机视觉等领域,在蕴含大量信息的同时也存在许多噪声与冗余信息,产生“过拟合”和“维数灾难”的问题。因此,对高维数据进行降维是十分有必要的。
降维方法大致可分为三类:有监督降维、半监督降维和无监督降维。有监督方法是在事先知道样本类别信息下进行降维;半监督方法根据少量已知类别和大量未知类别样本数据进行降维;无监督方法事先无样本类别信息,一般以保持样本间结构不变为原则进行降维。本文主要针对无监督降维方法进行研究。
在无样本类别先验信息下,样本间的局部结构和全局结构信息在降维过程中成为重要的考虑因素。文献[1]通过自适应投影保持降维前后样本间的局部几何结构尽可能不变;文献[2]通过L2,1范数构造相似矩阵图刻画局部几何结构;文献[3]尽可能保持所有样本间的相似关系不变;文献[4]通过谱聚类的引导学习全局稀疏子空间结构进行降维;文献[5]引入图正则项进行特征选择使得降维前后样本间的流行结构保持一致。
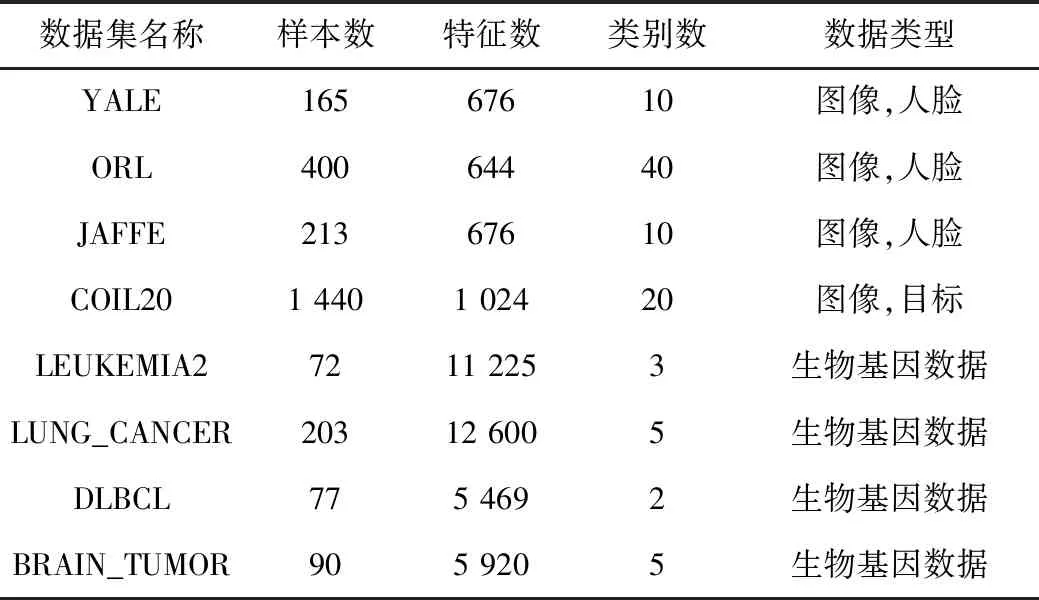
综上所述,多数降维方法只考虑样本间的单一结构,故本文提出基于L2,p稀疏子空间和局部结构保持降维方法,同时考虑样本间的全局子空间结构和局部几何结构,通过刻画局部相似性关系图,保持降维前后样本间局部流行结构一致;通过更一般化的L2,p范数约束(0 s.t.X=XZ,diag(Z)=0 (1) 其中,Z∈Rn×n为相似矩阵。‖·‖0表示对矩阵Z作稀疏约束。 在实际生活中,由于客观或主观原因,观测得到的数据往往含有噪声,因此松弛式(1)得到: s.t.diag(Z)=0 (2) 由于去掉diag(Z)=0约束条件也不会造成平凡解,故式(2)可等价于: (3) 其中,λ>0为平衡参数。由于L0范数求解过程中不可导,在全局优化时属于“NP难问题”,因而,往往对其进行近似求解,用‖·‖1或‖·‖2,1等近似求得稀疏解。 任意给定一矩阵B∈Rm×n,bi为B的第i行,bj为B的第j列,Bij为B的第i行第j列元素,对矩阵B定义Lr,p范数(r>0,p>0)如下: (4) 其中,‖b‖r是关于向量b的Lr范数。由式(4)可知,当r=2,p=1时,‖·‖r,p为L2,1范数;当r=2,p=2时,‖·‖r,p为Frobenius范数。由于L2,p(0 无监督降维方法在无样本类别先验信息下,样本间的局部结构和全局结构信息在降维过程中成为重要的考虑因素,多数降维方法只考虑样本间的单一结构因素。往往高维数据本质上存在于多个低维子空间中[6],子空间学习对样本数据重构,通过稀疏等约束,获得全局的子空间结构。文献[7]表明,在无监督降维方法中刻画数据的局部结构具有重要意义。局部结构可描述样本间的局部近邻关系,一般以k-近邻方法来刻画。同时,文献[8]表明,L2,P范数(0 基于上述考虑,本文提出基于L2,p(0 基于L2,p(0 (5) Sij= (6) 为避免平凡解,增加约束项PTXXTP=I,其中I为单位阵,目标函数(5)转化为: s.t.PTXXTP=I (7) 模型(7)有两个变量,本文运用交替优化方法求解P和Z,将问题分为以下几个阶段:固定P学习Z、固定Z学习P。 (1)更新变量Z:将P固定,Z的子问题等价于 (8) 式(8)对Z进行求导,令其导数为零,可得: AP-αXTPPTX+αXTPPTXZ=0 ⟹Z=(αXTPPTX)-1(αXTPPTX-AP) (9) (2)更新变量P:将Z固定,P的子问题等价于 s.t.PTXXTP=I (10) 利用拉格朗日乘子法,令 ρTr(PTXXTP-I) (11) 式(11)对P进行求导,令其导数为零,可得: XBXTP=ρXXTP (12) 其中,B=α(I-Z-ZT+ZTZ)+βL。投影矩阵P通过求解式(12)的广义特征值,由其前d个最大特征值所对应的特征向量组成。 在许多实际应用中,D>>n,在特征值求解过程中,若对式(11)直接进行求解,矩阵有可能出现不可逆的情况,且计算过程中的时间复杂度和空间复杂度都较高。参照文献[9],投影矩阵P可用样本的线性关系来表示,令P=XW,则式(11)可化为: s.t.WTXTXXTXW=I (13) 令K=XTX为核矩阵,Kij=K(xi,xj),样本通过核技巧被映射到Hilber空间,式(13)可转化为: s.t.WTKKW=I (14) 进一步考虑,可采用不同的核函数,对式(14)进行扩展。当其为线性核函数时,式(14)等价于式(13)。 L2,pSLPP算法描述如下: 算法:L2,PSLPP (1)输入:数据矩阵X,参数α、β、ρ和p (2)初始化:t=0,ε=10-8,maxIter=500,At=I以及Zt,Pt,Wt (3)repeat: (4)根据式(9)更新Zt+1; (5)根据式(12)或式(13)更新Pt+1; (6)更新At+1第i个对角元素p/2‖Pit+1‖22-p; (7)t=t+1; (8)until满足收敛条件{‖Pt+1-Pt‖∞,‖Zt+1-Zt‖∞}<ε或者t>maxIter (9)输出:降维后的样本矩阵Y=PTX 为验证本文方法的有效性,将本文所提的方法L2,pSLPP同6种先进的无监督降维方法对比:URAFS[5]、ANMMP[1]、LPP_L2、1[2]、KCRP[10]、SPFS[3]和CGSSL[4]。 实验选用8个公开的标准数据集:4个图像数据集(YALE,ORL,JAFFE,COIL20)和4个生物基因数据集(LEUKEMIA2,LUNG_CANCER,DLBCL,BRAIN_TUMOR),主要信息如下: (1)YALE:该数据集由耶鲁大学所搜集的人脸图像数据组成,包括165幅图,为15个人在不同光照、表情以及姿态下的人脸图像,每个人有11幅。 (2)ORL:该数据集由剑桥大学AT&T实验室所搜集的人脸图像数据组成,包括400幅图,为40个人在不同光照、争闭眼等表情以及其他细节的人脸图像,每个人有10幅。 (3)JAFFE:该数据集是关于女性面部表情的数据,包括213幅图,由10位女性的7种面部表情(开心、难过、生气等)组成,每种表情有3~4幅。 (4)COIL20:该数据集由哥伦比亚大学所搜集的目标识别图像数据组成,包括1 440幅图,为20个目标在不同旋转角度下的图像,每个目标有72幅。 (5)LEUKEMIA2:该数据集为白血病数据,包括72个样本,3种亚型白血病类型,每个样本的基因特征数有11 225个。 (6)LUNG_CANCER:该数据集为肺癌数据,包括203个样本,5种类型:4种不同患病类型和1种不患病类型,每个样本的基因特征数有12 600个。 (7)DLBCL:该数据集为淋巴瘤数据,包括77个样本,两组淋巴瘤类型,每个样本的基因特征数有5 469个。 (8)BRAIN_TUMOR:该数据集为脑部肿瘤数据,包括90个样本,5种类型:4种不同患病类型和1种不患病类型,每个样本的基因特征数有5 920个。 数据集描述如表1所示。 表1 数据集描述 本文所提方法的参数设置与对比方法的参数设置相同,近邻参数k=5,投影矩阵P维数空间为d,聚类个数为C。 若无具体说明,所有方法参数均采用“网格搜索”方式选取,平衡参数取值范围为{10-6,10-5,10-4,10-3,10-2,10-1,1,101,102,103,104,105,106},维数空间d取值范围为{5,10,15,20,25,30,35,40,45,50}。降维后的数据均通过K-MEANS聚类,实验结果用聚类准确率(ACC)进行比较。为避免随机性,每种算法均运行10次并取聚类准确率的均值。实验环境为Windows7系统,内存4 GB,所有方法用MATLAB 2015a编程实现。 观察p的不同取值对L2,pSLPP性能的影响。p的取值范围为{0.01,0.25,0.50,0.75,1.0},其他参数的设置同3.2节。对上述8个数据集观察p的不同取值下的平均聚类准确率(ACC),其中性能最优的通过加粗显示,具体如表2所示。 从表2可看出,L2,pSLPP的聚类准确率在不同数据集下随着对p的不同取值而变化,并且最优值不总是在p=1下取得,对所有的数据集并没有普适的最优p值。因此,相对于固定p=1,对不同数据集令p值保持灵活性是更为可取的方法。 表2 不同p值下L2,pSLPP聚类准确率 (%) 将本文L2,pSLPP与其他6种先进的无监督降维方法对比,观察上述8个数据集不同算法的平均聚类准确率(ACC),结果如表3所示。 由表3可看出,本文L2,pSLPP算法在上述数据集下均取得最高聚类准确率。对比LPP_L2,1和CGSSL稀疏子空间无监督降维算法,L2,pSLPP取得更优的聚类效果,这是由于L2,P范数约束(0 本文在降维过程中考虑混合结构,提出基于L2,p(0 表3 不同算法的聚类准确率 (%)1 相关工作
1.1 稀疏子空间结构
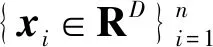
1.2 Lr,p范数
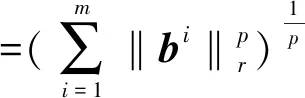
2 本文方法
2.1 基本思想与动机
2.2 目标函数
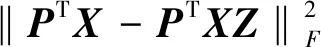
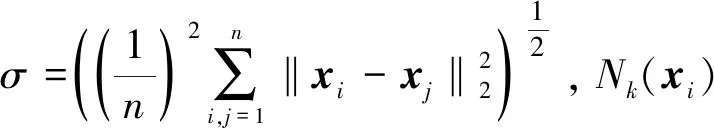
2.3 目标函数求解与算法
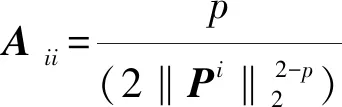

3 实验
3.1 数据集
3.2 参数设置
3.3 L2,p(0

3.4 同其他方法的对比
4 结论