基于成对约束的半监督聚类方法

陶性留，俞 璐，王晓莹

(1.陆军工程大学 通信工程学院，江苏 南京 210007；2.陆军工程大学 指挥控制工程学院，江苏 南京 210007)

0 引言

现实社会中，面临的数据越来越多，越来越宽泛，越来越复杂，同样数据特征的维度也越来越高。如何去挖掘有价值的信息一直是广受关注的热点。聚类是数据挖掘和模式识别的重要工具，它是将数据样本划分为不同的簇，使同一簇的数据样本具有较高的相似性，常见的方法有K-means[1-2]、FCM[3-4]等。而半监督聚类[5]作为半监督学习的一个重要分支，它以无监督的聚类算法为基础，通过利用少量的监督信息来提高聚类的性能。目前，半监督聚类中常见的先验知识表现为部分样本的类标签信息或是反映两样本是否归于同一簇的成对约束信息。所谓成对约束关系具体分为两种：

(1)两个样本同属于一个簇团(必须链接集Must-link，ML);

(2)两个样本属于不同簇团(不能链接集Cannot-link，CL)。很显然，这是一种相对较弱的指导信息，因为判断两个样本是否属于同一簇团要比判断它们分属于哪个簇团更加容易。通常可以通过生活经验或者常识来判断。

基于成对约束的半监督聚类方法的基本思想是利用先验监督信息来调整样本数据之间的作用力，根据少量被正确划分的样本数据，促使其近邻能被正确地划分，进而实现整个数据集的划分。该聚类算法通常在经典的算法框架下，合理设计出目标函数再进行一定程度的优化之后得到更加符合实际，更加令人满意的聚类算法。本文考虑在之前研究的FCM-NMF[6]算法上添加成对约束条件，以使聚类性能得到进一步的提高。

1 相关工作

1.1 NMF算法[7]

(1)

(2)

其中⊙是Hadamard积运算符，代表矩阵对应元素相乘。这时用系数矩阵HT代替原始矩阵，就可以实现对原始矩阵进行降维，从而减少存储空间，减少计算资源。

1.2 基于非负矩阵分解和模糊C均值的聚类方法(FCM-NMF)

通过利用非负矩阵分解独特的优势，不仅可以进行降维，而且物理意义明确。但也有可能破坏数据样本之间的本质结构，影响聚类效果。为了减少负面影响，希望在NMF压缩样本数据的过程中进行模糊聚类。对于大量高维数据，通过NMF提取样本的本质特征，同时保留作FCM模糊分析聚类，提出了新的聚类算法FCM-NMF。它将NMF分解对原始数据样本的影响加入到FCM的目标函数中，由交替迭代产生的新的低维表示矩阵可以用来描述样本之间的本质关系。改进目标函数如下：

(3)

式(3)中，λ≥0是平衡系数;第一项表示模糊C均值聚类框架，第二项表示利用NMF算法处理原始数据的过程对聚类的影响程度。

使用梯度下降法和交替迭代法解得各变量的更新公式如下：

(4)

i=1,2,···,c;j=1,2,···,n

(5)

i=1,2,···,c;j=1,2,···,n

(6)

(7)

H=H⊙[1×sum(Uf)]T

1.3 基于非负矩阵分解的约束聚类[8]

基于非负矩阵分解的约束聚类的主要思想在于：当给定数据集X、必须链接集ML和不能链接集CL时，希望通过借助非负矩阵分解的手段，在FCM-NMF的聚类框架中去寻找带有先验知识信息的系数表示矩阵H。可以构造以下目标函数：

(8)

其中定义了监督矩阵R，它是由先验知识构成的，反映了样本i与样本j之间的成对约束关系。

(9)

Must-link上两点之间的相似性被强制近似为1，CL上两点之间的相似性被强制近似为0。同时定义了价值系数矩阵A，其元数α与β表示所确定的ML与CL的重要性，其数值在0～1之间。

(10)

HHT是可以近似监督矩阵R，从而解决了利用系数表示矩阵来表示约束就成了问题，使得模型物理意义得以明确。然后，进行优化目标函数，利用交替迭代法求解出基矩阵W和系数表示矩阵H的更新公式：

(11)

(12)

2 基于成对约束的半监督聚类方法

2.1 模型建立

由相关知识可知，基于非负矩阵分解和模糊C均值的聚类方法(FCM-NMF算法)，其核心思想利用NMF作为特征提取的手段，为了尽可能不破坏样本之间的本质联系，将特征提取手段与聚类过程加以结合，融合NMF和FCM算法改变目标函数的形式，生成新的低维表示矩阵。该算法物理意义较为清晰，同时在实验中证明了其正确性和有效性。本节考虑将成对约束条件加入FCM-NMF的目标函数框架中，通过少量监督信息的引入，进一步改善聚类性能。改进的目标函数如下所示：

(13)

在公式(13)中，λ≥0是平衡系数，f是模糊系数，其值介于1～2.5之间。第一项表示模糊C均值聚类框架，hj到vi的欧几里得距离用dij表示。第二项表示加入了成对约束监督信息的NMF算法处理原始数据的过程对聚类的影响程度。当约束数量为0时，该算法退化为FCM-NMF算法。

2.2 模型求解

很明显，公式(13)的目标函数是非凸的，解出它的全局最优是不实际的。因此，利用交替迭代法则去探索非凸函数的局部最优解是一个可行的办法。通过迭代以下步骤来解决优化问题，直到目标函数收敛或超出阈值条件:

(14)

i=1,2,…,c;j=1,2,…,n

(2)固定W,H，U，通过V最优化J。V的更新准则为:

(15)

i=1,2,…,c;j=1,2,…,n

(3)固定V，H，U，通过W最优化J。W的更新规则与NMF算法一致，为:

(16)

(4)固定W，V，U，通过H最优化J。

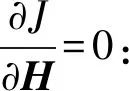
(17)

其中，H=H⊙[1×sum(Uf)]T。1 代表具有c行的全1向量，Uf是指U矩阵的对应每个元素的f次幂。利用梯度下降法得到以下附加的更新规则:

(18)

δ是控制梯度下降步长的参数矩阵。令

(19)

然后，能得到：

由于会展旅游业相关制度的不完善，也导致了成都市会展业和旅游业的融合不畅，由此导致会展旅游业的整体营销模式不成体系，发展滞后。目前成都市会展旅游业的营销模式主要还是以承办单位为主，很多会展虽然主办方为政府和行业协会，但是这些单位往往不会参与对展会的营销，而是由承办单位来进行营销宣传，但是其作用肯定是不如主办单位的影响力大。旅游管理部门很少关注会展旅游这一方面，在营销上也很少配合承办单位，常常出现会展旅游业中旅游业管理缺位的局面。承办单位在会展营销模式上也较为传统，缺乏创新。

(20)

H最终的更新公式为：

(21)

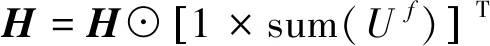
Ω=XTW+2(A⊙R⊙AT)H

+4(A⊙A)(H⊙H⊙H)

Λ=HWTW+2(A⊙(HHT)⊙AT)H

+4(A⊙A)(H⊙H⊙H)

2.3 聚类算法

基于成对约束的半监督聚类算法具体流程如表1所示。通过上述推导求解，可以获得基矩阵W，系数矩阵H，隶属度矩阵U，聚类中心矩阵V的更新表达公式。W是降维后的低秩空间的表现形式，H是原始数据X经降维后的低维表达方式，V是该聚类过程中所形成的簇中心向量的组合形式，而隶属度矩阵U是对所有样本进行软聚类的模糊隶属度的呈现方式，Uij越大，则反映样本j属于簇i的概率越大，可根据其获取样本的标签向量Y∈R1×n。

表1 基于成对约束的半监督聚类算法

3 实验结果与分析

3.1 实验环境与方法

在本节中，通过在wdbc数据集和wine数据集两个UCI验证集上的实验验证基于成对约束的半监督聚类算法的性能，包含在不同数量的监督信息的指导下其算法性能的变化情况和价值系数的变动对聚类准确率的影响。所有这些算法都是在MATLAB R2014a中实现的。将这些算法的最大迭代次数设置为10 000，并在接下来的所有实验中保持不变。针对每种算法实验，分别进行20次，并将实验数据结果平均值予以记录。表2显示了验证数据集的统计信息。并且选取了3种半监督聚类算法与之对比，分别是PMF[9]、SS-NMF[10]和CCSR[5]。

表2 验证数据集的统计信息

PMF算法分别将样本之间的约束关系ML和CL抽象为样本数据结构关系的正边和负边，而利用先验监督信息构造的邻接矩阵则是通过图正则化进行处理。SS-NMF是一种基于Symmetric NMF的约束聚类算法，它对满足ML的样本进行奖励，对违反CL的样本进行惩罚，同时修改样本的邻接矩阵。CCSR算法将数据点映射到一个新的特征空间，同时让其满足约束条件，它是图聚类的一种方式，支持非线性可分数据。

3.2 评价标准

对于每个数据集，选取准确率(ACC)、归一化互信息(NMI)和F度量(F-score)作为聚类效果的评价指标。下面的公式是本实验聚类的评价指标。

(22)

式中，TP是指在同一个类中聚集的两个文档是正确分类的，TN是指在同一个类中聚集的两个文档是正确分开的。FP表示不应该属于一个类别的文档应该属于错误的类别，FN表示不应该被分开的文档应该属于错误的类别。

(23)

聚类中常用NMI来衡量两种聚类结果的接近程度。PAB(a,b)表示A和B的联合概率分布，H(A,B)表示两类结果的联合熵。

(24)

(25)

(26)

F-score是一种考虑到信息检索的精度和召回程度，以便于不同技术或系统之间进行结果比较的测量方法。在上面的公式中，P和R分别表示信息的精度和召回率。上述三个聚类评价指标的取值均在0～1之间，指标值越大，聚类效果越好。

3.3 实验结果与分析

通过观察图1，从总体来看，随着约束对的增加，两个数据集上的聚类性能趋势上均朝着好的方向发展，在wdbc数据集和wine数据集上实验中其准确率最好可达95.86%和93.10%，较没有约束的聚类算法性能有着极大的改善，说明了成对约束信息确实可以指导聚类过程，同时也说明该算法优于FCM-NMF算法，验证了该算法的正确性和有效性。从细节上来说，在随着约束信息增加的有些过程，其算法性能不但没有提高，反而降低了。这也是一种合理的现象，原因在于，首先是约束信息是通过随机方式获取的，有些样本之间的关系对这个数据集结构刻画得更深入，而有些关系早已在FCM-NMF算法基础上明确，其指导聚类的过程意义不大。再者由于成对约束是一种弱指导信息，模型的输出样本也许不一定满足成对约束关系，有可能会衍生出输出模型与监督信息不一致的性能平衡问题。

图1 wdbc和wine数据集上聚类性能

图2显示了wdbc和wine数据集上价值系数α和β的变动对聚类准确率的影响。在两个数据集上分别加入九组和五组的约束信息，通过调节价值系数的数值观察其聚类准确率的变化情况。通过大量实验可以看出价值系数α与β设定对聚类性能的影响匪浅，它们反映了的半监督信息ML与CL对聚类的重要性。该参数的设定与数据集本身有着密切的关系。在本实验中，将wdbc数据集中α设为0.7，β设为0.5可以寻求到准确率的局部最优解。而在wine数据集中α设为0.8，β设为0.9可以寻求到局部最优解。

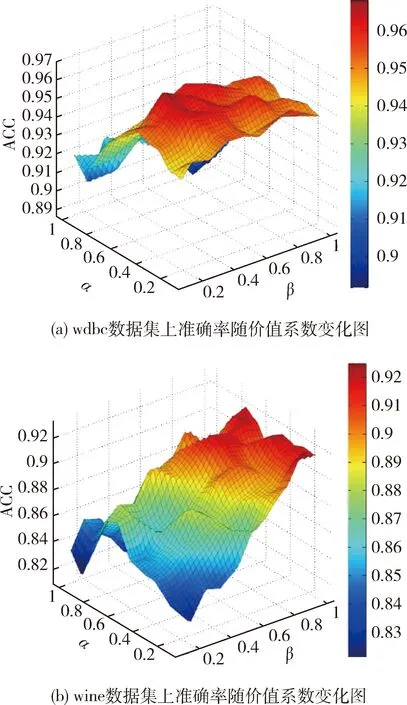
图2 wdbc和wine数据集上价值系数α和β的变动对聚类准确率的影响

图3显示了wdbc和wine数据集上各半监督聚类算法性能对比图。首先可以看到，在两个数据集上，随着成对约束数目增加，各算法均呈现上升趋势。再者，CCSR在wdbc数据集上的性能表现很好，但在wine数据集上性能很差，或许因为在wine数据集上的监督信息不够，不足以支持其达到最佳效果。相反SS-NMF在wine数据集上性能非常好，但是在wdbc数据集上其劣势却很明显。因为SS-NMF修改的是邻接矩阵，而不是直接改变目标函数。PMF算法总体性能良好，在验证集上，比无监督聚类准确率最佳分别改善可以接近10%和8%。相较于本算法差距比较明显，因为PMT在奖励ML时约束的提供了一个负项，这对于整体聚类意义不大。通过验证集的实验验证了所提的基于成对约束的半监督聚类方法的有效性和稳定性。

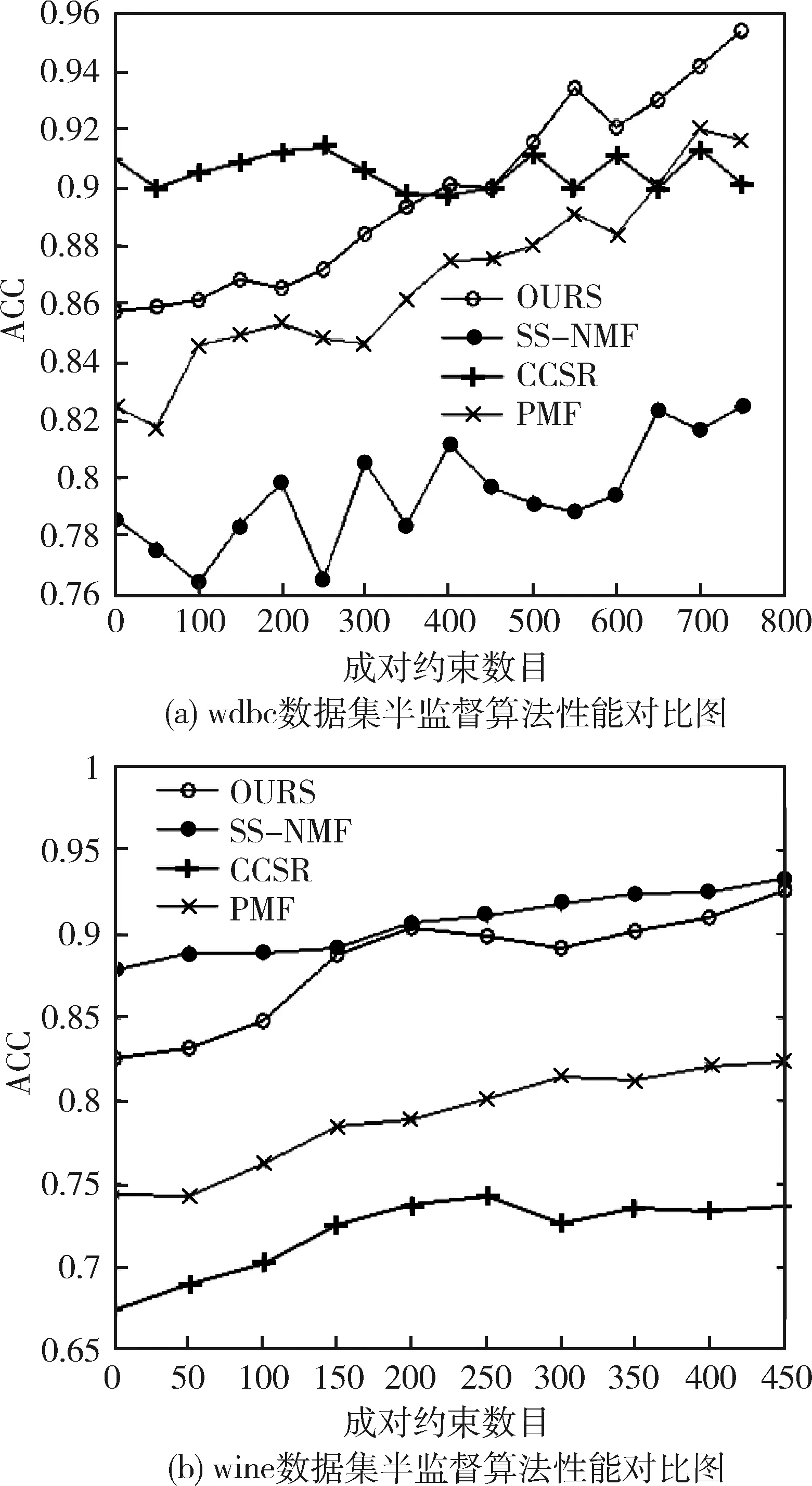
图3 wdbc和wine数据集上各半监督聚类算法性能对比

4 结论

本文提出了基于成对约束的半监督聚类方法。其核心思想是在FCM-NMF算法的基础上，依靠少量的成对约束监督信息的加入，改善整体聚类性能。但也有可能衍生出输出模型与监督信息不一致的性能平衡问题，有待作深入探讨。下一步考虑将成对约束条件作为监督信息应用于多视角聚类任务，并针对这个问题展开研究。