基于GE 混合规则的统计缔合流体方程预测CO2 在水中的溶解度

卞小强，熊 伟，蔺嘉昊，熊 武

（1. 西南石油大学 石油与天然气工程学院，四川 成都 610500 ；2. 中国石油 长庆油田分公司第三采气厂，内蒙古 乌审旗 017300；3. 中国石油 新疆油田分公司，新疆 克拉玛依 834000）

高含CO2天然气开发过程中气井普遍产水，水和CO2之间的相互作用规律目前仍未清晰［1-2］。大多数的高含CO2气藏中CO2处于超临界态，在形成氢键时CO2既可以作为电子受体也可以提供电子。Abudour 等［3］证实了CO2分子中碳原子作为电子受体、H2O 分子中氧原子作为电子供体，且比CO2氧原子作为电子供体和H2O 中氢原子作为电子受体形成的氢键更加稳定。他们还基于SAFT1-RPM 状态方程（EoS）考虑了CO2为3C、H2O 为4C 的缔合结构，从而建立了预测CO2在H2O 中溶解度的热力学模型，在引入固定的二元交互作用参数后，该模型能预测CO2在盐水体系中的溶解度［4］。Zhao［5］分别利用PC-SAFT 和tPC-SAFT 模型对CO2-H2O 体系相平衡进行了研究，结果表明CO2考虑为4C 缔合结构时，预测效果最佳。Duan等［6］通过SRK-CPA EoS 预测了CO2在纯水中的相行为，研究了CO2作为惰性、自缔合组分（2B，3B，4C）时，缔合结构对CO2-H2O 体系相平衡的影响，当CO2作为自缔合组分时，模型效果较差。

本工作基于GE（Huron-Vidal（HV））混合规则并结合改进的SRK-CPA EoS 模型，建立了一个预测CO2在水中溶解度的新模型（iCPA-HV），新模型考虑了水的自缔合和CO2-H2O的相互缔合，利用最小二乘法在278 ～573 K、0.1 ～140 MPa范围内，回归了模型的拟合参数（Eij，Eji，F）且关联成温度的函数，并与SRK-HV［7］和PRSV-WS［8］模型进行了对比分析。

1 热力学模型

1.1 状态方程

SRK-CPA EoS 的表达式见式（1）。

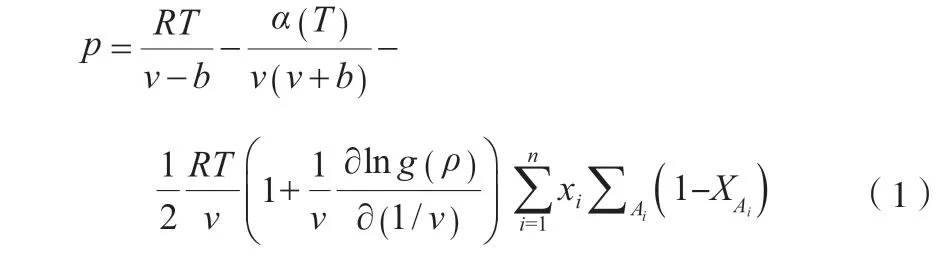
参数α（T）的表达式见式（2）。

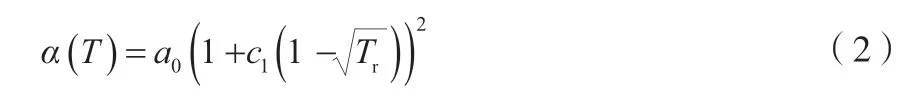
g（ρ）的近似表达式见式（3）。

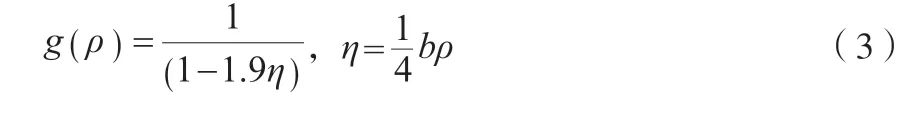
XA是缔合分子在A 缔合点处未与其他分子缔合的摩尔分数。未缔合分子的摩尔分数XA与缔合强度和摩尔密度有关，可由式（4）求得。

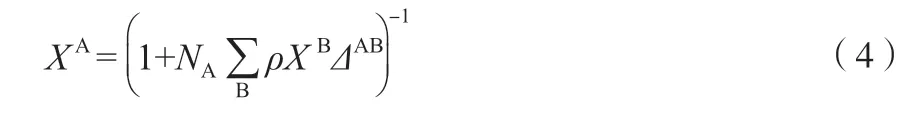
式中，B 表示分子上的缔合位；ΔAB为缔合强度，与摩尔体积和缔合能量有关，可由式（5）近似求得。

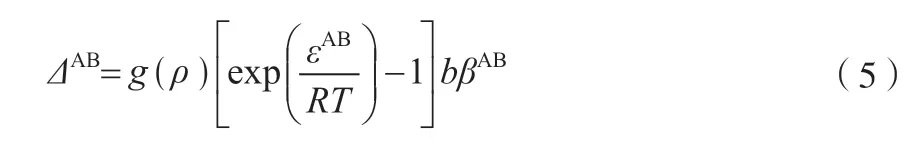
CPA（立方加缔和状态方程）中物理项中采用HV（基于超额Gibbs 自由能的混合规则）混合规则来代替vdW（范德华）混合规则以改善模型在高温高压下的性能。本工作假设CPA 中的交叉缔合作用只与水的缔合作用强度有关，并引入一个二元交互作用参数（F）描述二者之间的关系，F 表达式见式（6）。

SRK EoS 和PRSV EoS 具体的表达式分别参考文献［7］和［9］。

1.2 基于活度系数的混合规则

HV 混合规则见式（7）～（8）。

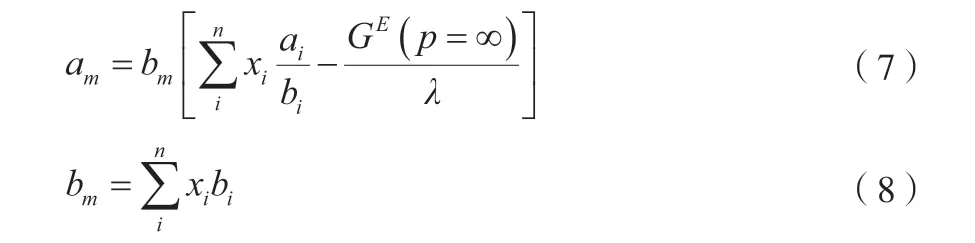
式中，GE为p=∞时的超额Gibbs 自由能。

WS（统计热力学）混合规则表达式见式（9）～（10）。

式中，kij为Zhao 等［8］修正后的参数。

此处，GE采用Huron-Vidal 修正的非随机二流体理论方程［10］计算，表达式见式（11）～（13）。

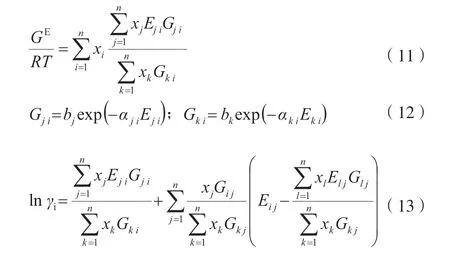
2 CO2 在水中的溶解度模型

iCPA-HV 模型（式（1）～（8）及（11）～（13））有4 个拟合参数（α，Eij，Eji，Fij），采用最小二乘法拟合大量文献实验数据（见表1），得目标函数，见式（14）。

CO2-H2O 体系拟合得到的关联温度的参数表达式见式（15）～（16）。

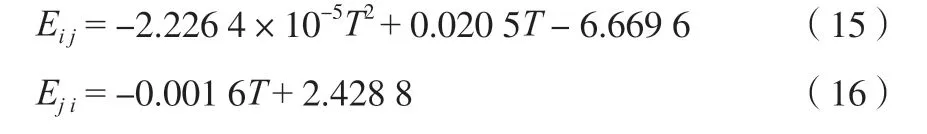
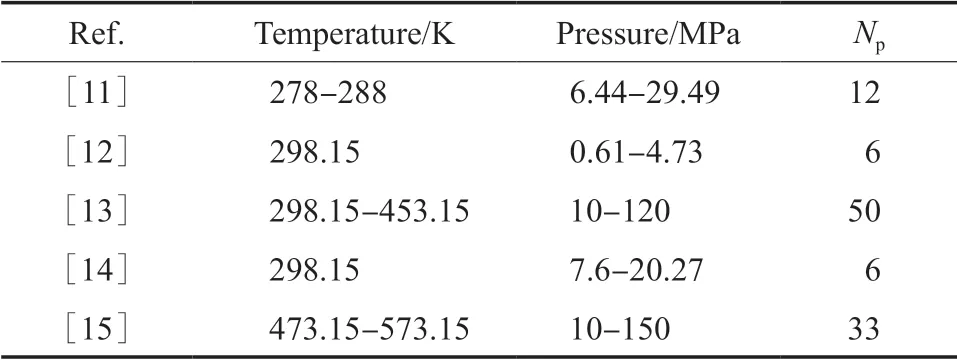
表1 CO2 在水中的溶解度数据Table 1 CO2 solubility data in water

在CO2-H2O 体系中，CO2接受一个电子与H2O 形成氢键，H2O 的缔合结构为4C，交叉缔合强度相互作用参数表达式见式（17）。

3 结果与讨论

对于CO2-H2O 体系，α 与温度无关，最优化后取0.1。为对比方便，定义了平均绝对相对误差（AARD）［16］，见式（18）。

图1 给出了不同模型的预测结果。由图1 可知，由于iCPA-HV 模型考虑了分子间的缔合作用，PRSV-WS 模型考虑了状态方程与第二维里系数的关系，均能较准确地预测CO2在水中的溶解度，而SRK-HV 模型只考虑到Gibbs 自由能，预测结果误差偏大。在278 ～573 K、0.1 ～140 MPa 范围内，iCPA-HV 模型预测CO2在水中溶解度的结果与实验数据有较好的一致性；PRSV-WS 模型在低温（小于333.15 K）下能较好地预测CO2在水中的溶解度，但温度高于513.15 K 时，模型的预测精度较差；SRK-HV 模型在低压（小于40 MPa）下预测结果较好，但不适用于高压（大于100 MPa）条件。

表2 给出了不同温度下3 个模型的计算结果误差。

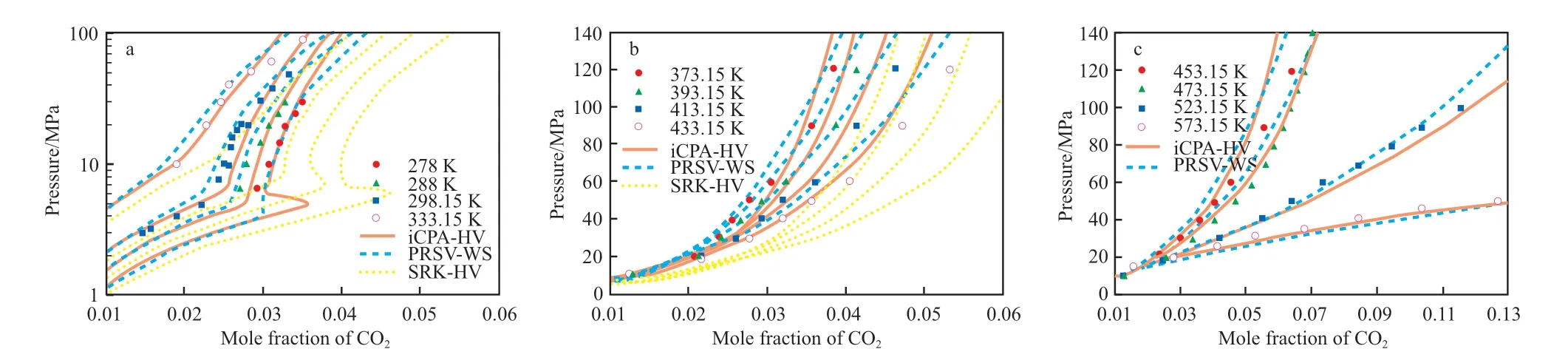
图1 CO2 在水中溶解度模型预测结果对比Fig.1 Comparison of prediction results of CO2 solubility model in water.

表2 CO2 在水中溶解度预测结果Table 2 Prediction results of solubility of CO2 in water

由表2 可知，在278 ～573 K 范围内，改进后的iCPA-HV 模型预测精度最高，AARD 为4.15%，其次是PRSV-WS 模型（AARD 为6.01%），最差的是SRK-HV 模型（AARD 为25.41%）。

4 结论

1）基于SRK-CPA 缔合流体方程和HV 混合规则，建立了预测CO2在水中溶解度的新模型iCPA-HV，该模型考虑了水的自缔合和CO2- H2O的相互缔合，且模型中的拟合参数可关联成温度的函数。

2）与PRSV-WS 和SRK-HV 模型的对比结果表明，在278 ～573 K、0.1 ～140 MPa 范围内，iCPA-HV 模型具有最高的预测精度（AARD 为4.15%），结合第二维里系数的PRSV-WS 模型次之（AARD 为6.01%），而只考虑了超额Gibbs 自由能的SRK-HV 模型预测误差最大，AARD 为25.41%。

3）新建的iCPA-HV 模型不仅能精确计算CO2气体在水中的溶解度，还为其他气体在水中的溶解度计算提供了一种新思路。

符 号 说 明

a SRK 方程的参数，（MPa·cm2）/mol

a0a 方程的系数，常数

b SRK 方程的参数，cm3/mol

c1α 方程的系数，常数

E 混合规则中的二元相互作用参数

F 组合规则中的二元交互作用参数

G Gibbs 自由能，状态函数

GEp=∞时的超额Gibbs 自由能，状态函数

g(ρ) 径向分布函数

kij二元交互作用参数

NA与A 点缔合的分子数，等于2

p 压力，MPa

R 通用气体常数，8.314 J/（mol·K）

T 温度，K

Tr对比温度，K/K

v 摩尔体积，cm3/mol

XAi为i 分子在缔合位A 未缔合作用的摩尔 分数，%

XB缔合分子在B 缔合点处未与其他分子缔 合的摩尔分数，%

x 摩尔分数，%

xexpCO2在水中的溶解度实验值，%

xcalCO2在水中的溶解度的模型计算值，%

α 非无规参数

βAB交互作用体积

γ 活度系数

ΔAB缔合强度，关于摩尔体积和缔合能量的 函数

εAB缔合能量，（MPa·cm3）/mol

η 对比密度

λ 常数，λ=lg2

ρ 摩尔密度，cm3/ mol

下角标

i，j，k，l 不同化学组分

m 混合组分