让解决问题不“难”解决

沈芳

【摘要】数学是一门具有高度的抽象性、严密的严谨性和广泛的应用性的学科。解决问题是小学数学教学的总体目标之一。一直以来，解决问题是学生数学学习中的一座高山，登不上爬不过。如何切实提高学生解决问题的能力，让解决问题不“难”解决？我们应从知识基础、肢体功能、语言表达、思辨能力四方面入手。

【关键词】解决问题 解题思路 数学能力 数学思想

随着年级的升高，学生在解决问题中常常出现瓶颈，找不到门路，摸不清思路。为什么会这样？笔者认为，中高年级解决问题涉猎范围愈加广泛，有些远离了学生的生活实际。如何让学生在解决实际问题时不再一筹莫展？我们的教学应教给学生一种能力，一种思想。数学思想是数学的灵魂和精髓，也是解决问题的基本策略。

一、倒带再现，调取基础知识资源

数学知识呈螺旋递进式发展，具有很强的连贯性。既然在高年级解决问题时会困难重重，何不将这一知识倒回至低年级，让学生看看题目最初的模样，找回最初的感觉，从而找到解题的思路。

例如，苏教版数学五年级下册《简易方程》中列方程解决稍复杂的实际问题，原题是：“北京颐和园占地290公顷，其中水面面积大约是陆地面积的3倍。颐和园的陆地面积和水面面积大约各有多少公顷。”此题需要根据“陆地面积+水面面积=颐和园的占地面积”这一等量关系式来列方程，而问题正在于很大一部分学生察觉不到其中的等量关系。究其原因，学生对于占地面积、陆地面积、水面面积比较陌生。那怎样让其提高熟悉度呢？这时可以调取学生的基础知识资源。问：“苹果有30个，橘子有24个，共有多少个水果？”这题你会吗？那是自然。继续问：解题思路是怎样的？苹果个数+橘子个数=水果总个数。那么，回到原题：在这里陆地面积和水面面积相当于苹果和橘子，占地面积相当于水果总个数，现  在你能找到这题的等量关系式列出方程吗？

投以一块铺路石，通过例举追问、倒回再现，学生豁然开朗，找到了方法、明晰了思路。之所以以水果为例，是因為水果与学生生活没有距离，在解决熟悉事物的问题时，学生们是有直觉思维的，在解题时问题自然能迎刃而解。

二、手势比画，发挥肢体记忆功能

人有五官，各有作用。在数学教学中，更多注重发挥嘴巴的作用，而忽略了其他的作用。曾有人说：好的课堂一定是“五官苏醒”的课堂。五官的充分参与，才能有效调动学生的积极性与参与度。

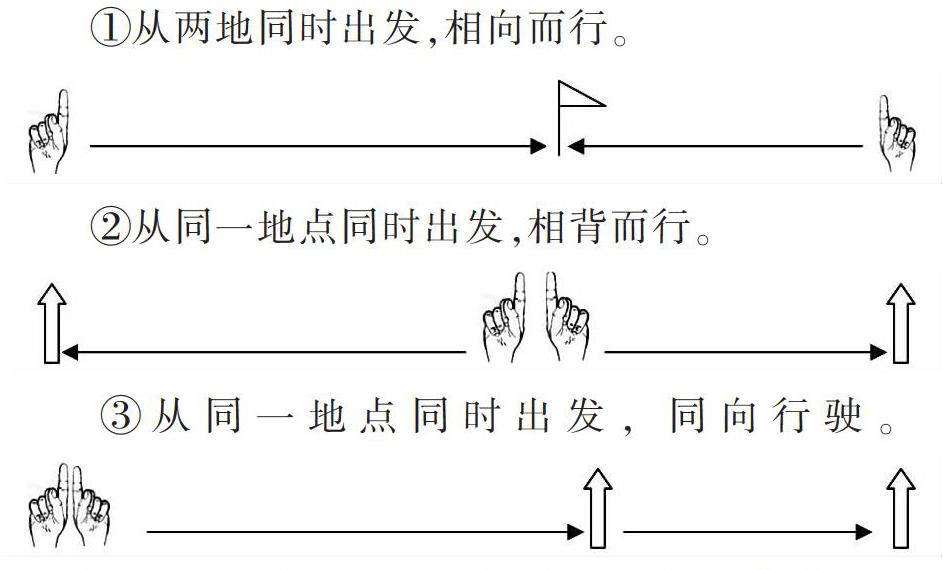
在相遇问题中，尽管建议学生用画线段图的办法来理清数量间的关系，但多数学生怕麻烦而不愿画图，从而影响了解题。鉴于此，在教学中引导学生通过用手势比划来描述题意，感受题目的动态变化，帮助学生分析题意。

①从两地同时出发，相向而行。

②从同一地点同时出发，相背而行。

③从同一地点同时出发，同向行驶。

然后组织学生比较三种情况的联系，使学生明白：前两种尽管出发点不同、方向不同，但其中的数量关系却是相同的，“甲行驶的路程+乙行驶的路程=总路程”或“甲乙速度和×时间=总路程”。而第三种看似与第二种差不多，实则完全不同，数量关系是“甲（快）行的路程-乙（慢）行的路程=相距路程”或者“甲乙速度差×时间=相距路程”。

有时手部的一个简单动作，反而能发挥大能量。主要因为学生亲身经历的总会有一种熟悉感与亲密度，久而久之学生会将其内化为自身动作直觉，通过比划、分析，抛开具体情境发现问题本质，帮助学生超越具体情境，向抽象思维水平迈进。

三、能说会道，强化语言表达能力

在数学课堂中，学生语言表达一直是个大难题，尤其在解决问题中，学生对题意道不清说不明。如何打破僵局呢？应让学生站在舞台的“正中央”，经历教师引说、学生范说模说，在生生带动中，逐步引导学生敢说、善说，从而强化语言表达能力。

如苏教版数学五年级下册《简易方程》中的一道习题：甲、乙两辆汽车同时从同一地点出发，相背而行，2.4小时后相距216千米。甲车的速度是42千米/时，求乙车的速度。由于是练习课，教师便放手让学生独立思考解答，互相说解题思路。在此过程中，教师“退一退”，换得学生“进一进”，把话语权交给学生。

生1：因为这题属于相遇问题中的第二种情况，可以根据“甲车行的路程+乙车行的路程=总路程”这一数量关系列出方程：42×2.4+2.4x=216。

生2：也可以根据“速度和×时间=总路程”，列出方程（42+x）×2.4=216。

数学语言水平低的学生在课堂上对数学信息的敏感度差，语言之间的转换不流畅，思维显得缓慢，造成数学知识接收、处理起来很困难。因此，清晰流利的语言表达，更能看出学生的数学能力。在解决问题的教学中，更要训练学生“能说会道”，从而达到思维与语言同步发展的目的。

四、巧思妙想，提高理性思辨能力

小学阶段主要涉及的数学思想有对应、假设、类比、符号化等，数学思想较之数学基础知识，有更高的层次和地位。它蕴含在数学知识的发生、发展和应用过程中。只有掌握了数学思想，才能在分析和解决问题时得心应手;只有领悟了数学思想，才能使其真正变成自身的能力。

苏教版数学五年级下册第一单元《简易方程》练习三中，安排了多道列方程解决实际问题。

第12题：沪宁高速公路全长大约274.08千米。一辆轿车和一辆大客车分别从上海和南京同时相对开车，轿车的速度是118.4千米/时，大客车的速度是110千米/时。经过几小时，两车在途中相遇？这题是相遇问题，解题思路有两种：轿车行的路程+客车行的路程=总路程;速度和×时间=总路程。

第13题：李老师买两种书，一共用去83元，其中《历史故事》有4本。《历史故事》每本12元，《森林历险记》每本7元。《森林历险记》有多少本？虽然这题不是相遇问题，但与前两题有相通之处：买《历史故事》用去的钱数+买《森林历险记》用去的钱数=总钱数。

第14题：小张和小李用25分钟合打了一篇6000字的稿件。小张平均每分钟大约打130个字，小李平均每分钟大约打多少个字？这题虽然情境又有变化，但解题思路也有两种：小张打的字数+小李打的字数=总字数;两人打字的速度和×时间=总字数。

在这里，如果教学中只是简单地叠加，学生必定产生畏难情绪。于是，课堂上组织学生思考解题思路，再集中出示解题思路，让学生们在观察分析中寻找联系。学生会发现，尽管情境不同，但从数学角度看，却有着共同的模型。在这里运用类比思想把题目读薄，由一组题简约为一类题，使学生领略数学思想的魅力，从而提高理性思辨的能力。

数学是简洁的，学生会觉得数学越来越难，是因为没能寻找到行之有效的方法和思想。教师应帮助学生在繁杂中理清头绪，在抽象中还原本质，激活学生思维，引导学生自主建构，切实提高学生解决实际问题的能力。

【参考文献】

[1]牛献礼.在问题解决中感悟模型[J].小学教学设计，2018（12）.

[2]乔张娥.如何提高学生分析和解决数学问题的能力[J].小学教学设计，2018（12）.