基于动态时间规整的磁偏角修正地磁匹配导航算法∗

保金宏，尚俊娜∗，施浒立

(1.杭州电子科技大学通信工程学院，杭州310018；2.中国科学院国家天文台，北京100012)

导航技术作为是一门古老且不断发展的涉及多学科交叉的工程技术，随着时代的发展在军用和民用领域一直起着巨大的作用。随着多学科的发展与互相交叉，导航系统向着无源性、实时性、隐蔽性等方面发展[1]。目前应用的导航技术有惯性导航、卫星导航、天文导航、地形匹配导航以及地磁匹配导航等[2]。作为无源导航，惯性导航在较短位移时间内具有较高精度，常常被应用在海洋、平原、水下等环境条件下，但是其导航误差会随着时间的延续而增大。应用的最为广泛的是卫星导航，因为它具有覆盖范围广、精度较高、使用方便等优点，但是在特殊环境下有时会无法正常接收到有效信号。天文导航能够提供位置信息和姿态信息，但是存在传输信号不连续、信号易受气候条件影响等缺陷[3]。地磁与重力匹配导航方法相似，其中重力匹配导航的重力仪造价较贵[4]，影响推广使用，尤其难以在民用领域应用。

地磁场是地球的基本物理场，地磁场中任意一点的地磁矢量都不尽相同，并且地磁矢量与地理经纬度之间存在一一对应关系。因此，只要确定该点的地磁场矢量，便可通过与己有地磁图比对，找到该点的地理位置，实现全球定位[5-7]。地磁导航虽然在空间位置上有一一对应的关系，但是在实际导航定位应用时，单独的地磁导航定位计算量大，在地磁图地磁强度差异性不突出的地方又容易造成误匹配等原因，约束着它的推广应用。

由于组合导航拥有改善精度、提高可靠性，扩大工作地理空间[8-9]等长处。为此，把地磁导航和惯性导航进行组合，通过加速度计输出的加速度和模块解算的航向角得出载体的运动轨迹，通过运动轨迹限制地磁匹配的搜索范围，利用地磁匹配去修正惯性导航产生的累积误差。其中文献[10]提到的地磁相关匹配算法需要在一定范围内平移惯导的指示航迹得到待匹配模板，并通过一定的相关准则找到与真实航迹上磁场值序列最相关的待匹配模板作为匹配结果。但是实际采样过程中，相同运动轨迹上的采样时间不一致，导致两者的序列长度不一致，因此需要将在线采集到的序列与数据库中地磁序列进行映射，再通过相关匹配算法解算运动轨迹。

本文在无里程信息辅助的地磁导航中，采用动态时间规整的地磁匹配方法，定位精度能达到5 m以内，克服了无里程信息地磁匹配导航容易出现较大误匹配的问题。在基于里程信息辅助的地磁匹配中，由于低成本的导航定位模块精度较差，需通过对磁偏角进行数据库采样，用于补偿惯性器件解算时的航向角，经过补偿后的航向角和模块输出的加速度得出运动轨迹，利用运动轨迹缩小地磁匹配的搜索范围，通过地磁匹配的方法修正惯导的累积误差，使得低成本的导航定位模块的定位误差精度可达到1 m以内。相较于高成本、高精度的惯性器件模块采用惯导加地磁匹配的方法获得亚米级定位精度，本文的方法使得低成本的导航模块具有更广的应用范围。

1 无里程信息辅助的地磁导航

在实际的地磁匹配过程中，若不严格按照对应地磁数字图中的位置来采集数据，通常不能直接用于地磁信息序列间的匹配。参照动态时间规整方法DTW(Dynamic Time Warping)[11-12]，即如何衡量两个长度间隔不一的时间序列，实现相似度匹配的一种方法。通过该方法来解决地磁序列匹配过程中，在不同时间序列长度情况下，采集信息的匹配问题。如图1所示。

图1 时间序列之间误匹配示意图

从图1可知，A、B两点位于不同时间序列同一长度上，但不能直接匹配，A点位置的物理相似点应为另一条时间序列的点A′。因此采用DTW的方法对两条时间序列之间进行匹配。

假设离散数据库中待匹配的地磁场强度序列为A＝[a1，a2，…，an]，在线测量得到的地磁场强度序列为B＝[b1，b2，…，bm]，他们的长度分别为 n和 m。

若n＝m，则可以直接采用欧式距离的方法进行匹配。

若n≠m，应采用动态规整的方法，先使这两个序列对齐，构造n×m的网络矩阵(c，r)，矩阵元素为ac和 br，两点间的距离为 d(ac，br)，(即寻找序列 A的每一个点ac和B的每一个点br之间的相似度关系，d(ac，br)的距离越小，则认为相似度越高。)一般采用欧式距离，即 d(ac，br)＝(ac-br)2。 该方法寻找一条通过此网格中若干格点的路径，路径通过的格点即为两个序列进行计算对齐的点。

首先定义一条路径为规整路径W，规整路径Wk＝(c，r)为两序列A与B的映射，有:

但是，在最佳规整路径的解算过程中，规整路径W需要满足以下条件:

①边界条件:

离线阶段与在线阶段采集地磁的速度有所不同，但地磁特征排列的先后顺序不会改变。通过边界条件可以限定所选的规整路径的起点是由矩阵网格的左下角出发，终点在矩阵网格的右上角结束。

②单调性条件:

若 Wo-1＝(r′，c′)，则路径下一点 Wo＝ (r，c)需满足:

式中:c和r分别为矩阵网格点的横坐标和纵坐标，此单调性条件限制了规整路径W是随着时间单调前行。

③连续性条件:

若 Wo-1＝(r′，c′)，则规整路径下一个点 Wo＝(r，c)需满足:

此条件限制了规整路径W在匹配时只能与自己相邻的点对齐。保证序列A与B的每个坐标都在W中出现。

综合连续性和单调性约束，每一个格点的路径就只有三个方向。假设路径已经通过了格点(r，c)，那么下一个通过的格点只可能是下列三种情况之一:(r＋1，c)，(r，c＋1)，(r＋1，c＋1)。

在动态时间规整算法中，满足上述三个约束限制的路径有数条，DTW所求的是其中规整代价最小的路径:

式中:K为补偿系数，对不同长度的规整路径W做补偿。DTW算法的目的是求得将两序列规整后距离度量最小的规整路径，因此为求得此路径，定义累加距离:从(1，1)点开始匹配两序列A与B，规整路径每经过一点，之前所经过的每点的计算距离都会累加，至终点(n，m)时，累加距离即为所有匹配点的总距离之和，亦即序列A与B的相似度:

式中:L＝(c，r)为点ac与br的欧氏距离到达该点的最小的邻近元素的累积距离之和。求得最小累积距离之和，即求得了最小规整代价的规整路径D，从而完成对离线阶段与在线阶段地磁数据的动态时间规整，进而求得两序列的相似性，完成地磁特征相关性匹配的解算。

2 基于磁偏角补偿和里程信息辅助的地磁导航

2.1 地磁匹配算法

地磁匹配算法实质是一种数字地图匹配算法。在文献[13]中介绍了目前三类地磁匹配的方法:其中一类方法是按照相关性准则强调他们之间的相似程度，如互相关算法(COR)、相关系数算法(CC)、积相关算法(PROD)和归一化积相关算法(NPROD)；另一类方法强调他们之间的差别程度，如平均绝对差算法(MAD)、均方差算法(MSD)、绝对差算法(AD)、平方差算法(SD)；而第三类方法则是基于Hausdorff距离的相似算法(HD)。在计算最佳匹配点时，第一类算法求极大值，另两类则取极小值。

文献[13]对基础地磁匹配方法进行了对比，从匹配精度和匹配运算量来看Hausdorff距离方法总体性能最佳。故我们采用Hausdorff距离方法对小车测量的磁场强度与解算位置对应的地磁强度做分段相似度比较。

Hausdorff距离原理[14-16]如下:

给定欧式空间中的两列点集为 Q＝{q1，q2，…}，P＝{p1，p2，…}，Hausdorff距离就是用来衡量这两列点集间的距离。

在本文中Q代表着小车在线移动测量得到的一组地磁场强度序列，P代表着经过磁偏角补偿后的航位推算在进行地磁匹配解算之后的位置对应的一组地磁数字图上的磁场强度。

2.2 基于磁偏角补偿和里程信息辅助的地磁匹配导航实现流程

基于磁偏角补偿和里程信息辅助的地磁匹配导航实现流程如图2所示。

根据实现流程系统框图，对模块定位轨迹解算过程进行详细阐述，具体介绍如下:

步骤1 对待匹配区域建立离散地磁场强度和磁偏角数据库[17]。

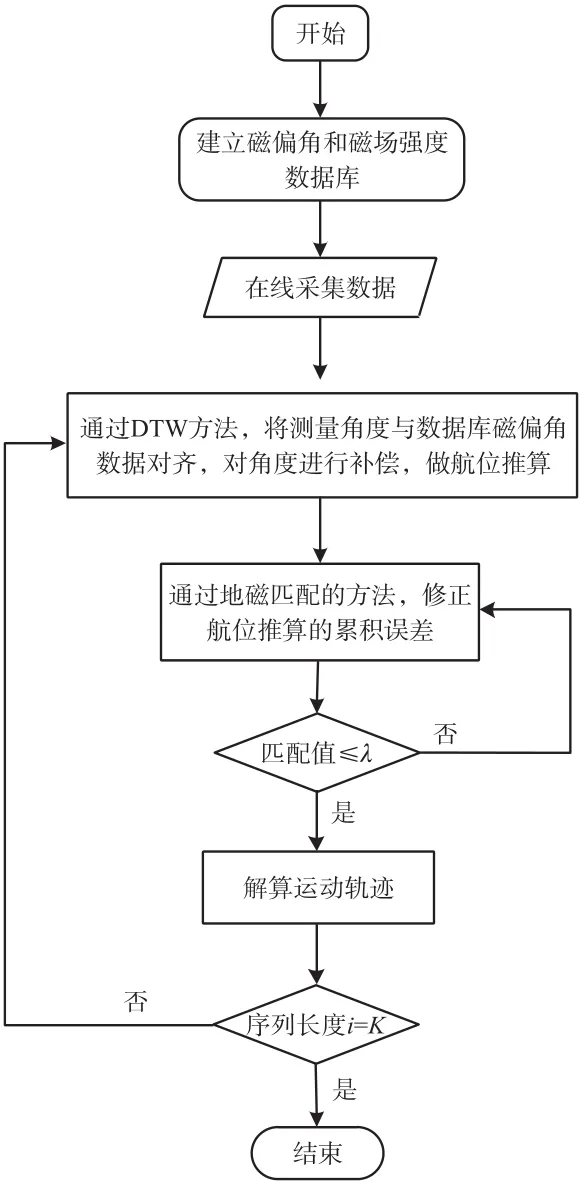
图2 实现流程系统框图

步骤2 随机给定一个初始位置，然后通过小车上装有的JY901自身惯性模块和地磁模块，得到一段地磁数据序列(m1，m2，…，mk)，其中 m＝(mx，my，mz)，以及惯性器件模块所测得的一组加速度序列(a1，a2，…，ak)和方位角序列(θ1，θ2，…，θk)。

航位推算原理:假设在 tn时刻，已知位置ptn(xtn，ytn)和当前时刻运动速度 vtn，及航向角 θtn，还有该位置磁偏角σθtn，这时通过航位推算求tn＋1时刻位置 ptn＋1(xtn＋1，ytn＋1)，计算公式为:

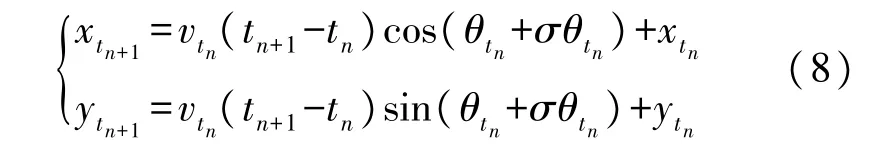
式中:磁偏角[σθt1，σθt2，…，σθtn，…，σθtk]是通过以模块初始位置的角度为真实角度对后面采样的角度求差值，保存在磁偏角数据库中，同时由于离散采样的磁偏角信息与实际采样过程的角度信息不是完全一一对应关系，通过动态时间规整方法，将在线测量的角度与磁偏角数据库中的角度进行映射，即得出实际测量位置所需要的角度补偿值。

步骤3 惯性器件在短时间内具有导航精度高的特征，但是随着时间的积累，器件本身的定位累积误差会逐步增大，故需要引入地磁匹配方法去修正误差。通过测量达到的三轴磁场强度去做欧式距离匹配优化，其方法如下:

式中:(mix，miy，miz)代表以位置 ptn(xtn，ytn)为中心，l为半径范围内对应地磁数字图上面的三轴磁场强度，求出在该范围内与测量的三轴磁场强度最为接近的点，作为修正点更新位置ptn(xtn，ytn)。

步骤4 在上一个修正点location(Xtn-1，Ytn-1)到location(Xtn，Ytn)在数字地图上的路径，(注:(Xtn-1，Ytn-1)≠ptn-1(xtn-1，ytn-1))对应得到一组地磁场强序列Q＝{q1，q2，…qi}，在两个修正点之间采样得到一组地磁场强序列 P＝{p1，p2，…，pj}，且 i≠j，通过采用动态时间规整的方法，将Q和P两组场强序列的长度整合成一样长，假设长度为 t，且 t≥max(i，j)，通过采用Hausdorff距离的方式判断两序列的相似性，若Hausdorff(Q，P)≤λ，则判断两序列匹配程度较高，修正点位置正确。λ是由地磁传感器模块的测量精度所决定[18-19]，将模块静置，测量一段时间磁场强度，得出模块测量误差范围，通过hausdorff距离的方法，解算出λ值。若H值大于λ，则对整合后的序列采用二分法进行判断，若是前半段的两个序列的匹配值小于或等于λ值，则对两个修正点的中心位置进行三轴地磁强度匹配；若是前半段的两个序列的匹配值大于λ值，则对修正点location(Xtn-1，Ytn-1)重新定位，取磁场强度匹配值仅大于最小值所对应的位置进行修正，则再重复步骤2中的航位推算，直到步骤4的过程，直到对小车运动位置解算完毕。

3 仿真实验

3.1 无里程信息辅助的地磁匹配导航实验仿真

在无里程信息辅助的地磁导航中，不具备横向空间识别的能力[20]，因此在应用环境中重点应用于管廊、单车道等一维路径的场景中，在线采集地磁序列过程中，保持在线采样路径与离散地磁数据库采样路径一致。我们的测试环境选用在中科苏州地理科学与文化信息园区大厦内的地下车库里，用小型履带车搭载JY901模块，通过JY901自带的地磁传感器测量地磁场强度，模块输出数据频率为10 Hz。对待导航区域进行数据采样，从初始位置开始，每间隔1 m进行一个点磁场强度数据进行采样，每个采样点上采集50个数据，通过拉依达准则去除粗大误差，然后做均值处理，得出该采样点的三轴磁场强度值。在图3中，“O”代表采样点的位置，然后对采样点之间做一维广义延拓插值处理[21]，得到离散的地磁数据库。

图3 在地下车库进行地磁数据采样

在图4中，图4(a)代表的是在车库中采集到的沿Y轴的地磁场强度序列离散数据库的数据。图4(b)是在实测过程中得到的沿Y轴的地磁场强度序列值。可以看出在线采样得到的地磁序列与数据库中对应的地磁场强度序列具有较高的相似性，采用DTW匹配的方法，对三轴矢量磁场强度分别去做匹配。得出图5的模块运动轨迹图，其中初始坐标为(46.5，27.5)。

图4 数据库地磁序列与在线采集地磁序列

在图6中“∗”代表地磁匹配定位的位置，箭头代表运动方向。在定位解算过程中，对于采样得到的三轴磁场强度序列，若有两轴及两轴以上的磁场强度序列匹配到同一个点，则代表匹配成功，匹配成功率为91.03%。图6中，左图中的“-∗”曲线代表匹配定位解算的误差值，从图6中可看出其最大定位误差为4.9 m。从右图可知，曲线代表定位误差范围，由图所示地磁匹配定位误差分布在4.65 m(97.7%)以内。

图5 基于DTW算法的室内定位轨迹图

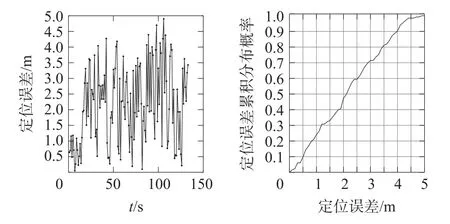
图6 无里程信息辅助的DTW算法匹配定位误差

3.2 基于磁偏角补偿和里程信息辅助的地磁匹配导航实验仿真

本节实验论证采用磁偏角补偿的航位推算加地磁匹配的方法使得低成本JY901模块的定位精度，可以接近高成本、高精度LINS354模块采用惯导加地磁匹配组合的定位精度。

在实验过程中采用的低成本JY901模块，其解算航向角的过程融合了地磁场信息，相较于同类只包含相同陀螺仪、加速度计模块，其解算航向角的累积误差较小，由于JY901模块在解算过程中融入了地磁场因素，因此在解算航向角的过程中易受到室内建筑物结构环境干扰，所以需要引入磁偏角对其航向角所受到的影响进行补偿。

电子磁罗盘通过感知周围地磁场的分布来计算地磁北极的方位，在室内环境中，建筑物的结构、强电场等因素都会对地磁场造成影响，使电子磁罗盘测量角度产生偏差。同时因为建筑物和室内的布局较为恒定，对地磁场的影响也较为恒定。

本文用搭载HMC5843磁传感器芯片的电子磁罗盘和JY901自带地磁传感器模块对室内环境下的磁偏角和三轴磁场强度进行采样。测试采用高精度LINS354模块与搭载地磁传感器模块的JY901，输出频率均为50 Hz。测试环境选择中科苏州地理科学与文化信息产业园区大厦，如图7所示。

图7 室内测试场景

制作磁偏角和地磁场强度数据库，具体步骤如下:

①选择长为10 m宽为5 m的开放办公区为待采样区域，并将测试区域按网格划分，确定采样点位置，如图8所示。其中“∗”为采样点位置。

图8 走廊办公区采样点分布

②将电子磁罗盘和地磁传感器放在图8对应的“∗”处，电子磁罗盘和地磁传感器方向指向坐标系相同，每个点采集50组数据。

③对每个点采集的50组数据通过拉依达准则去除粗大误差，然后做均值处理，得出罗盘在每个点的测量均值与坐标真实方向的平均误差值，以及该采样点的三轴磁场强度数据值。

④用广义延拓逼近法[21]处理采样值，使离散采样点形成一个连续的函数，覆盖整个采样区域。

首先在实验过程中，高成本、高精度惯性器件LINS354解算的航向角具有较高精度，且随时间累积航向角误差较小，不受建筑物结构的影响。同时利用高精度的LINS354模块进行数据采集得到定位轨迹不需要进行磁偏角补偿，定位轨迹如图10所示。

在图10中，坐标(2.1，2.3)为初始位置，箭头代表LINS354模块运动方向，“-∗”曲线为真实导航定位轨迹，“-o”曲线为未经处理的航位推算定位轨迹，“-o”曲线为经过地磁匹配修正的导航定位轨迹。

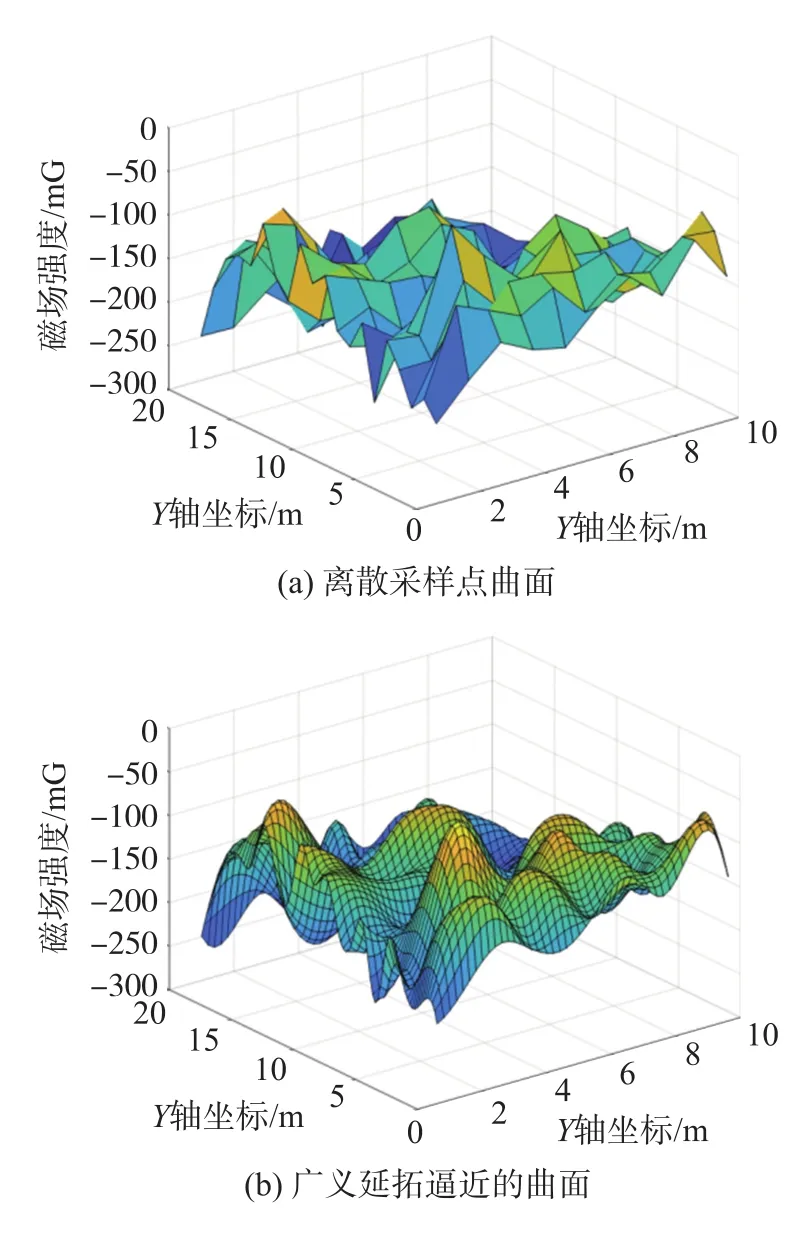
图9 室内环境地磁强度曲面

图10 LINS354模块采用不同方法时的定位轨迹

表1 LINS354采用不同方法时的定位精度

从图10和表1中可知，在运动距离较短时，LINS354的航向角误差较小，可以取得较好的轨迹相似性，但是由于加速度计的累积误差导致在行走过程中与真实定位轨迹的偏差较大，但通过地磁匹配修正累积误差的方法，仍然可以在94.85%的情况下取得亚米级定位精度。

其次在对JY901模块定位精度实验分析中，需要通过动态时间规整的方法，将实际测量得到的航向角与地磁数据库中数据进行映射，然后对测量角度进行补偿，如图11所示。

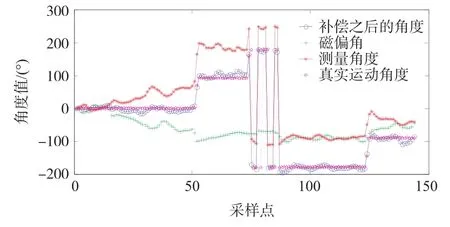
图11 JY901模块测量角度与补偿之后的角度曲线

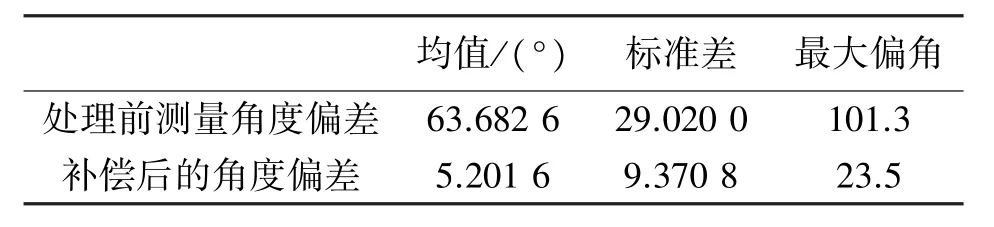
表2 JY901模块角度处理前后误差值比较

在图11中，“-∗”曲线为测量角度，“-＋”曲线为模块采样点对应磁偏角，“-o”曲线为经过磁偏角补偿后的角度，“-(”曲线为定位轨迹真实角度。由图可知未经过磁偏角补偿的测量角度与真实角度最大偏差可达101.3°，其与真实角度偏差的均值可达63.7°，标准差为29°；经过磁偏角误差补偿之后的测量角度与真实角度的最大偏差为23.5°，其与真实测量角度偏差的均值为5.2°，标准差为9.4°，由此可见，经过磁偏角误差补偿的角度可以获得良好的精度。不同方法的JY901模块定位轨迹如图12所示。

图12 JY901模块采用不同方法的定位轨迹

在图12中，坐标(2.1，2.3)为初始位置，箭头代表JY901模块运动方向。“-∗”曲线为真实定位轨迹，“-x”曲线为未经磁偏角补偿的航位推算定位轨迹，由于JY901模块的航向角的解算过程融合地磁信息，在室内受到建筑物钢结构影响较大，导致模块测量的航向角有较大的偏差，其中受建筑物影响最大偏角可达101.3°，运动轨迹严重偏离真实轨迹，其直接采集得到的航向角不宜为地磁匹配的直接参数，需要对航向角偏移误差进行补偿，经过角度补偿之后，航向角的最大偏差不超过23.5°。图中“-＋”曲线为磁偏角补偿的航位推算定位轨迹，由于单独依赖磁偏角的角度补偿不足以修正JY901模块的累积误差，所以还应同时引入地磁匹配方法，“-o”曲线为基于磁偏角补偿的地磁匹配导航定位轨迹。其中λ值由JY901自带的地磁传感器模块经2.2节中步骤四所述方法得到，设为3.563。

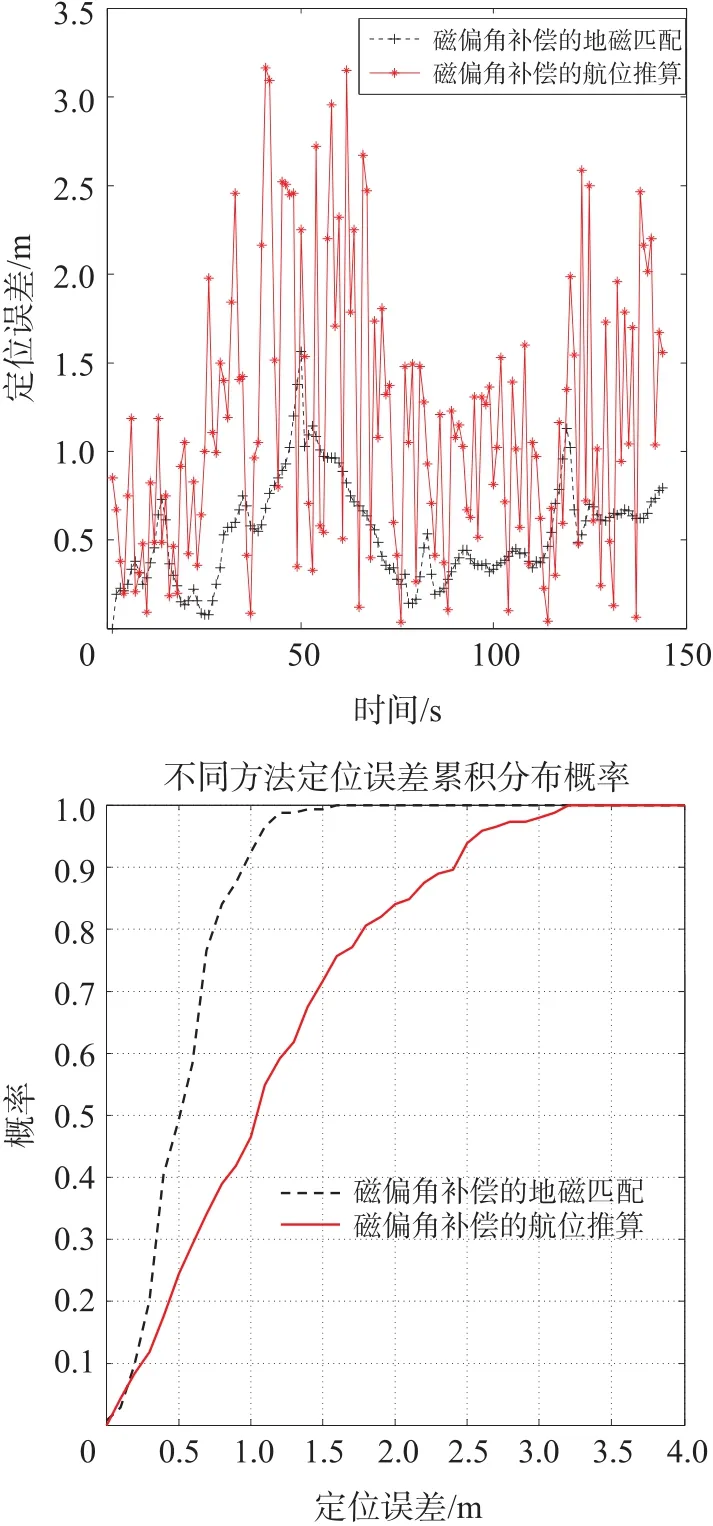
图13 JY901模块采用不同方法定位精度的比较

在图13中，对JY901模块基于磁偏角补偿的航位推算定位精度与基于磁偏角补偿的地磁匹配进行比较，得到:基于磁偏角补偿的航位推算定位精度最大误差为3.225 m，定位误差处于2 m以内的精度可达84.72%。基于磁偏角补偿的地磁匹配定位最大误差为1.687 m，定位误差在1 m以内的精度可达93.75%。从表1和表3中可知，低成本的JY901模块通过磁偏角补偿的航位推算结合地磁匹配的方法可以接近于高精度LINS354模块采用惯导加地磁匹配方法的定位精度。

表3 JY901模块采用不同方法定位的精度比较

4 结论

本文探索了地磁匹配导航方法，通过动态时间规整实现了一维路径的无里程信息辅助的地磁匹配导航，其精度可达4.65 m(97.7%)以内。同时利用高成本、高精度模块LINS354与经过磁偏角补偿航向角的JY901模块进行比较，在经过磁偏角补偿之后的低成本JY901模块的航位推算定位精度可达2 m(84.72%)以内，接近于高精度LINS354模块的航位推算定位精度。且通过地磁匹配方法修正磁偏角补偿后的航位推算的累积误差，使得JY901模块可以得到亚米级的定位精度，降低应用成本。