基于MIMU车轮力传感器姿态解耦方法研究∗
孙利成,王 东,张为公,许 曈
(东南大学仪器科学与工程学院,南京212000)
车轮力传感器(Wheel Force Transducer,WFT)[1]作为测量车轮与地面之间的接触力的装置,是衡量车辆运动性能的重要工具。WFT在汽车制动性能,道路谱的数据采集以及汽车动力学系统试验中得到了广泛的应用,对汽车动力性、制动性、操纵稳定性、悬架特性和路谱数据采集等提供有效的参考价值[2]。
与一般的六维力传感器不同的是,WFT与车轮固连,车轮力的测量坐标系(车轮系)与解算坐标系(车体系)不一致,导致测量结果与车轮姿态(旋转、倾侧、偏转)相互耦合。所以,对WFT进行姿态解耦至关重要。东南大学在WFT方面研究较为深入,在旋转解耦方面,主要利用绝对式编码器的输出进行车轮力解算,林国余等提出了车轮旋转角度在线标定方法[3],但是编码器在测量时存在诸多问题[4],如图1所示,汽车转弯时编码器产生的偏转角度将引入车轮力的解算偏差。所以本文借鉴了航姿参考解算方法,需要根据车轮的运动状态对车轮的姿态进行解算。在姿态解耦方面,崔晓阳等为了减小惯性传感器的漂移误差和系统噪声,分别对两种姿态解算算法进行了比较分析[5],常健等基于振动环境中惯性传感器的数据特征,设计了一种自适应变步长平滑滤波器用于平滑振动加速度,融合角速度信息,实现惯性传感器在振动环境下的姿态解算[6]。Shuaiyong Zheng[7]等提出了一种基于二分搜索和插值的旋转角度解算方法,适合单轴旋转。于家福[8]等提出了一种全新的MEMS偏航角速度传感器技术方案,实现了稳定回路的闭环控制。但是上述的姿态解算环境是在低速下进行的,由于陀螺仪量程有限,对于车轮高速转动不能适用,因此解决车轮高速转动下的姿态解算就显得尤为重要。

图1 车轮力传感器安装位置
本文提出一种基于微型惯性测量单元(MIMU)车轮力传感器姿态解耦方法,实现车轮姿态动态测量,可以有效解决上述问题,经过模拟实验和实车实验,能够获得更为真实的车轮力。
1 解耦方法基本框架
本文设计的车轮力传感器姿态解耦算法总体结构如图2所示。
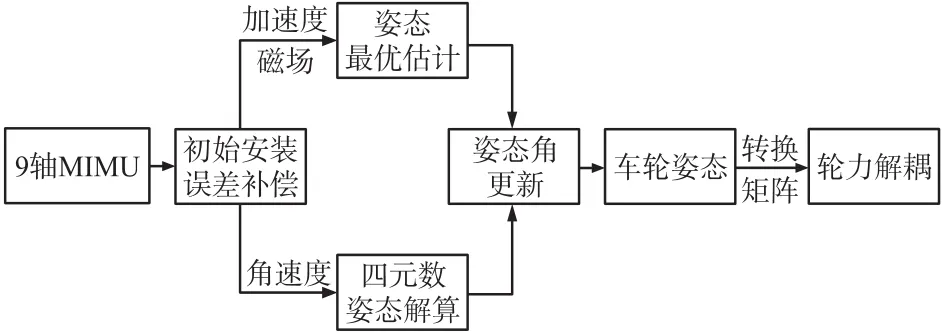
图2 姿态解耦方法基本框架
首先,利用一个9轴MIMU测出静止状态下的初始车轮的加速度、角速度和磁场进行初始安装误差补偿;然后利用梯度下降法对加速度和磁场进行车轮姿态的最优估计;再者,利用陀螺仪输出的角速度进行四元数的微分方程的解算,与加速度、磁场进行姿态角更新,为下次的姿态解算提供初始四元数,最终得到车轮姿态和转换矩阵,并且进行车轮力传感器的姿态解耦。
WFT测量的车轮力是地面对车辆车轮的直接作用力,是车辆车轮受到的力和力矩的统称[9],如图3所示,分别为纵向力Fx、侧向力Fy、垂直力Fz、侧倾力矩Mx、扭矩My和回正力矩Mz。在车辆行驶的过程中,WFT随车轮一起转动,解算的车轮力是基于车轮坐标系下的,和车轮的转动无关。需要得到车轮坐标系与传感器坐标系之间的关系实现车轮力的解耦。但是,车轮的运动状态不仅仅只有转动,还有倾侧和偏转,因此对车轮的姿态测量成为车轮力传感器姿态解耦的关键。

图3 车轮受力示意图
2 车轮姿态测量和轮力解耦
2.1 坐标系的建立与姿态角描述
为了描述车轮在运动过程中的姿态,分别建立车轮坐标系(n系){Onxnynzn}和传感器坐标系(b系){Obxbybzb},如图4所示,其中,On在车轮的中心,xn、yn和zn是车轮坐标系的轴,分别定义为车辆前进的方向,沿车轴的方向和垂直于地面的方向,轴Obxb、Obyb和Obzb绕Ob旋转,在初始情况下,两坐标系重合,当车轮绕轴Obyb旋转时,旋转的角度为横滚角φ,当车轮转弯时,绕轴Obzb偏转的角度为航向角ψ,车轮绕轴Obxb倾侧时,角度为俯仰角θ。
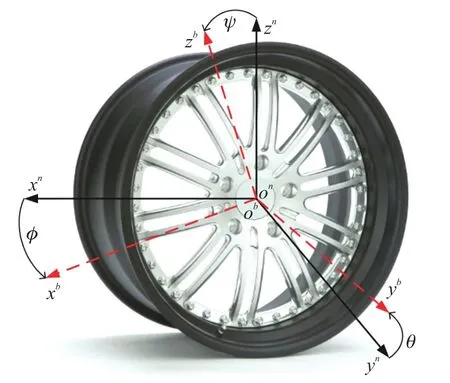
图4 车轮坐标系与传感器坐标系
当车轮力传感器进行旋转解耦时,车轮坐标系与传感器坐标系之间存在如式(1)所示的转换关系[10]:
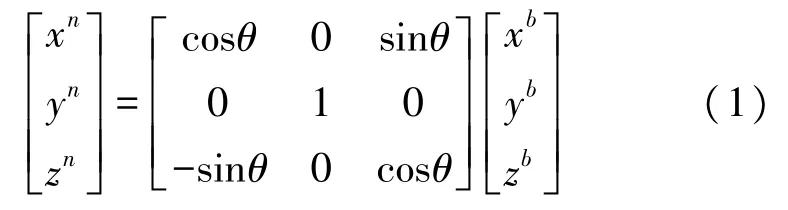
但是当车轮存在偏转和侧倾时,车轮坐标系和传感器坐标系之间存在如式(2)所示的关系,两坐标系之间的旋转矩阵为Cbn,式中c和s分别代表cos和 sin。

在传感器坐标系下测得的六维力转换到车轮坐标系下的六维力如式(3)所示:

式中:力矩 Mn=[MxnMynMzn]T,力 Fb=[FxbFybFzb]T,[]T为矩阵的转置。
定义姿态四元数 q=q0+q1i+q2j+q3k,其中 q0为四元数 q 的标量,q1、q2、q3为 q 的模长,i、j、k 为单位矢量,且i2=j2=k2=-1,则旋转矩阵可以用四元数表示为[11]:

2.2 车轮姿态测量
车轮力传感器的姿态仅仅利用编码器测得转角是远远不够的,因为在车辆的行驶过程中,车轮的偏转和侧倾编码器是无法测得的,所以,使用MIMU进行车轮的姿态角的测量。为了降低传统航姿参考算法的计算复杂度、提高实时性,本文根据MIMU中陀螺仪的输出ω,通过姿态四元数递推方式来求解当前车轮姿态^qω,t,从而通过式(4)中的进行轮力的解耦,求解过程如式(6)所示,车轮姿态解算算法流程如图5所示。
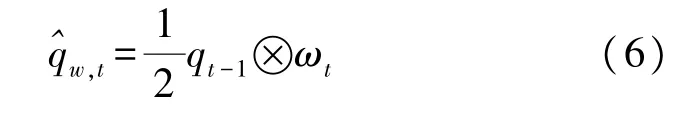

图5 车轮姿态解算算法流程图
其中,目标函数minfg,b(^qest,t,a,^b,m)的建立依据是求解当前姿态四元数^qest,t,使得重力场g与地磁场^b在该姿态中的投影与加速度计和磁力计的测量值误差最小。增益β用来修正由陀螺仪零均值测量误差引起的四元数微分计算误差,可通过陀螺仪输出估计四元数与目标函数估计四元数在散度相等条件下求解。增益α用来修正陀螺仪零偏漂移误差,可通过零偏变化率估计与归一化目标函数估计四元数求解。递推式姿态四元数的迭代初值可在车辆静止时,通过加速度计与磁力计的输出求解。
2.3 基于梯度下降法的姿态误差补偿
车轮的转速一般用陀螺仪测量得到,但是陀螺仪动态范围小、精度低、抗冲击能力差,并且由于角速度的积分产生累积误差[12],所以需要通过加速度计和磁力计进行误差补偿,车轮力传感器的姿态解算采用梯度下降法[13]进行数据融合。首先,将gb与^αb相减,构造梯度下降法的误差向量函数如式(7)所示:

式中:αx、αy、αz为加速度计的测量值。
对四元数求偏导,得到误差向量函数的雅克比矩阵Jg(q),如式(8)所示:

则梯度为∇f(q,^αb)=(q)·fg(q,^αb),
同理,由磁力计的输出值 mx、my、mz可以得到磁力计的误差函数

式中:^b=[0 bx0 bz]为标准化后地面参考坐标系中的磁场强度。则雅克比矩阵Jb(q,^b)为
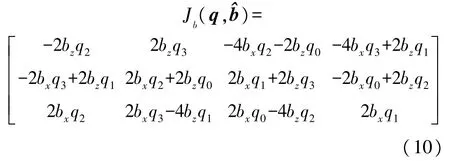
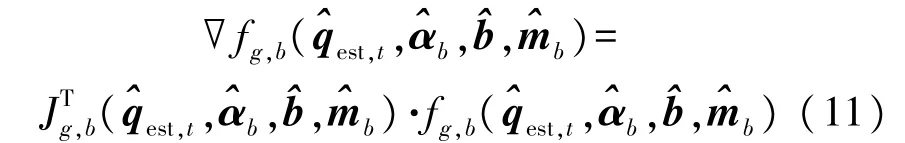
将梯度归一化∇fg,b/‖∇fg,b‖,其中‖∇fg,b‖为误差函数梯度的范数,得到最优四元数:
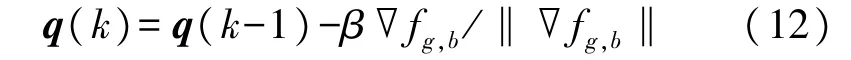
式中:β为步长。当β较大时,可有效跟踪车轮高速运动下的姿态变化,但静态情况下的姿态角精度得不到保证。而当β较小时,姿态角静态值虽然比较稳定,但四元数收敛速度慢。因此,要根据车轮的运动状态进行动态调整[14]。
3 实验结果
为了验证姿态解耦的可靠性和正确性,本文设计并进行了数学仿真实验,设计车轮行驶路线如图6所示,设定车轮转速1 rad/s,采样时间为25 s,采样间隔为10 ms。

图6 车轮行驶路线
由图7算法与仿真对比图可见,本文算法能够很好地跟踪车轮的运动状态,从横滚角对比图可以看出,车轮以在0~25 s以1 rad/s角速度旋转,从俯仰角对比图可以看出,车轮倾侧的角度在0~1°之间,车轮无偏转,从偏航角对比图可以看出,车轮在0~5 s,车轮无偏转,5 s~6 s逐渐右转 15°,并持续2 s,接着车轮回正,在 14 s~16 s左转 15°,并持续2 s,最后回正。计算仿真和算法之间的角度误差,如图8所示,实验结果表明误差在1°内,算法准确度较高。

图7 仿真和算法解算对比图

图8 仿真和算法角度误差
为了更加真实地模拟车轮运动环境,仿真时分别给陀螺仪、加速度计和磁力计加上如下表的噪声和漂移,以及机械振动,再次进行仿真对比。

表1 噪声强度和漂移参数
图9是加速度计和陀螺仪带噪进行的仿真对比实验。

图9 加速度计带噪解算对比图
由图10所示,因为加速度计受振动影响较大,横滚角和俯仰角误差有所增加。

图10 加速度计带噪角度误差
图11是磁力计和陀螺仪带噪进行仿真对比实验。

图11 磁力计带噪解算对比图
由图12所示,磁力计的噪声和漂移对偏航角的解算带来更多的误差。

图12 磁力计带噪角度误差
图13是陀螺仪、加速度计和磁力计都带噪的对比实验。

图13 带噪仿真和算法解算对比图
由图14所示,当加速计和磁力计都带噪时,横滚角、俯仰角和偏航角误差都有所增加,误差在2°之内,能够满足车轮力的解算。

图14 带噪仿真和算法角度误差
根据系统架构设计了姿态解耦硬件电路板如图15所示。

图15 姿态解耦硬件电路
为了模拟汽车姿态,运用自行设计的转台如图16所示,实验转台由电路板、滑环、联轴器和电机组成,并用编码器进行误差对比分析。

图16 实验转台示意图
首先进行静态测试,由图17所示,本文设计的姿态解耦算法不会因为陀螺仪的累积误差而发散,并且较快收敛。

图17 姿态解耦算法静态测试
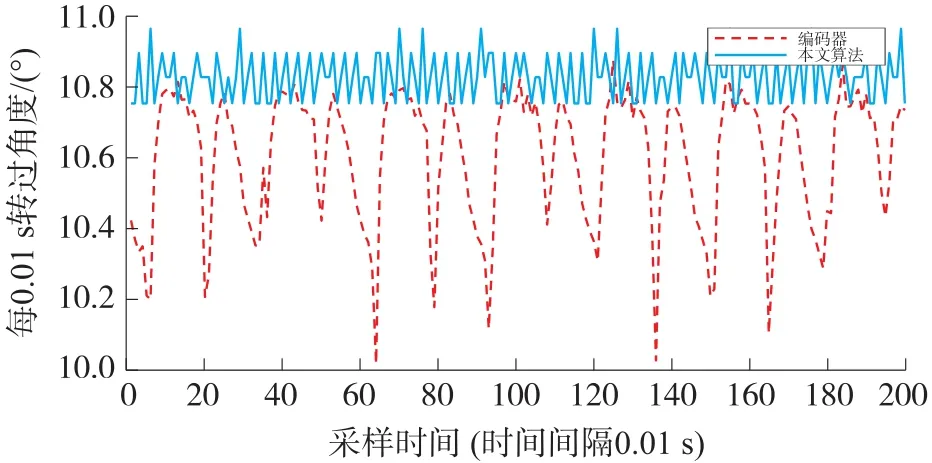
图18 本文算法与编码器转动角度对比图
然后将本文设计的姿态解耦算法与编码器转动角度进行对比,由图18所示,发现误差在1°内,本文设计的算法可以代替编码器进行车轮力传感器的旋转解耦。同时,在车轮旋转的过程中,不仅仅只有一个维度的旋转角度,如图19所示,俯仰角和偏航角都有输出,实现车轮的全姿态解耦。
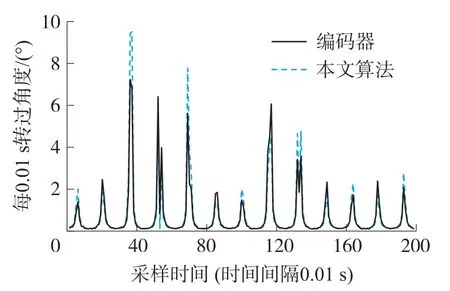
图19 俯仰角和偏航角变化图
4 结束语
本文根据车轮力传感器的轮力解耦,提出了一种基于MIMU代替编码器进行轮力的旋转解耦,并且对车轮在运动时进行姿态测量的方法,借鉴航姿参考解算方法,利用梯度下降法实现姿态的误差补偿,实现车轮力传感器的姿态解耦。实验结果验证了本文提出的姿态解耦算法的可行性。

