“一题多解”型习题教学之我见

王 锐

（江西省永修县九合中心小学，江西 九江 330300）

在小学数学教学中，“一题多解”型习题占有很大比例。所谓“一题多解”，指在一道题中同时存在几种不同的解答方式。由于此类习题通常要求学生同时列举出多种解答方式，相对普通习题而言，它提高了要求，增加了难度，故此学生在解答时往往只知其一，不知其二；甚至不知所云，无从下手。为了解决这一问题，笔者认为：在“一题多解”型习题的教学当中，应该尝试运用扩散思维。

一、理论研究

扩散思维，即发散性思维，是一种由事物的单一属性出发进行思考转向对事物的各个属性逐一思考，从而多途径地分析、解答实际问题的思维模式。乍看起来，这种思维方式甚为玄妙，远离生活，其实它在我们的日常生活、生产中广泛存在。例如人们在解决电力来源问题上就运用了“扩散”，分别利用水力、火力、风力、核能来发电；又如人类为了更好地利用电脑，结合电脑计算的可靠性和快捷性进行繁杂数据处理，结合电脑存贮的超大容量进行图文资料管理，结合电脑的智能性进行自动生产等等。这些实例均是通过不同的思路得到解决问题的多种途径，从而达到某个既定目标，而以上诸多途径的取得，归根结底不都是成功运用扩散思维的结果吗？

既然扩散思维在日常生产、生活中广泛运用，而且运用后都取得明显效果，那么在“一题多解”型习题教学中能否同样适用呢？我们不防从现行教材中寻求答案：

[题目]滨河公园原来有20条船，每天收360元。照这样计算，现在增加了15条船，每天一共收多少元？

这是第七册第五章第二节中的一道例题，对于这道题的解答，教材中是这样引导学生思考和解答的：

想：要求增加15条船后每天一共收入多少元，要先算出平均每条船收入多少元和现在一共有多少条船。由此得到解法一：360÷20×（20+15）。

想：要求增加15条船后每天一共收入多少元，还可以先算出平均每条船收入多少元和15条船收入多少元。由此得到解法二：360+360÷20×15。

现行教材中类似以上的例子还有很多，在此不一一列举，仅从上述例题中我们仍不难发现：例题的不同解法从不同的角度分析题中的数量关系，从而得到相异的思路，使例题出现不同解法。从这一点上将其与前面列举的日常生产、生活实例相互对照，我们很容易发现两者在解决问题的思维方式上是相同的，也就是说现行教材在“一题多解”型例题的解题思路编排上同样渗透了“扩散”思想。故此，我们可以断方：扩散思维在“一题多解”型习题的教学中同样适用。

二、实践探索

扩散思维在“一题多解”型习题的解答中的极大作用已不容置疑，那么在数学中就应当大胆尝试，基于这一点，本人在课堂教学过程中用“扩散”引导思考进行了以下探索。

小学生思维的发展水平仍处在初级阶段，存在着既活跃又盲目的两重性。故此，教师在教学中应当扬学生之长避学生之短，结合每道习题的特点，精心、合理地设计教学方案，将扩散思维渗透到所设计的教学方案中去，将学生活跃的思维顺着利于习题解答的方向引导，同时使学生在长期的潜移默化中初步掌握扩散思维的方法，最终达到解答习题和让学生自己学会“扩散”的双重目的。如我在教学一道组合图形面积计算题时是这样设计教学方案的：

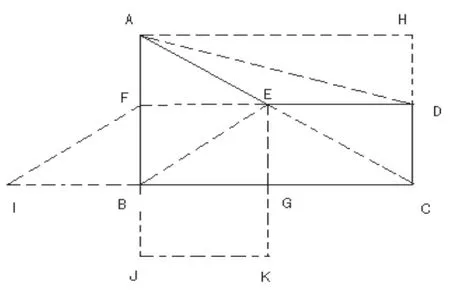
[题目]计算右图形的面积。你能想出

不同的解法吗？（第八册练习十二）

（仅列出思路引导过程）

出示图形，给出讨论题：这个图形能“割”成我们学过的图形吗？有几种“割”法？

学生操作学具，教师巡视辅导。

交流“割”法，并整理、解答。

（四种：沿EF割下；沿BE割下；沿EG割下；沿CE割下。）学生每说出一种割法便立即引导学生找出计算时所需的边长，列式解答，同时依次保留割下的图形。

引导扩散：

①启发：你能把刚才每次割下的图形重新“拼”成我们学过的图形吗？有几种“拼”法？

②学生操作学具，教师巡视辅导。

③交流拼法并整理、解答。（两种：拼成梯形CDFI；拼成梯形AEKJ。）同步骤3完成，保留拼成梯形CDFI的两个图形。

再次扩散：

①出示保留图形启发：用三角形在长方形上量一量。你发现了什么？

②学生操作，教师巡视辅导。

③交流。（长方形恰好与四个三角形等大，整个图形与五个三角形等大。）

④你能为这道题再发明一种解法吗？

学生尝试扩散：

①观察原图形，问：同学们还能想出其他的解法吗？

②学生独立思考。（酌情引导学生用“补”法。）

③交流并解答。（两种：补成长方形ABCH；补成梯形ABCD。）

小结：（略）

在以上教学方案中，本人首先从“割”图形入手，同时调动学生的多种感官，在讨论题中留出大量的思考空间，让学生积极思维，大胆操作，从而得出四种解法。接着便着重运用扩散引导学生将“割”这一条思路拓展到“割”、“拼”、“量”三条思路，解题方法由四种增加到七种。最后我特意将剩余两种解法留给学生自己独立探索，旨在检验学生自己的扩散能力。在整个教学过程中，由于做到了“割”、“拼”、“量”、“补”四管齐下，不仅使习题的解答方式在学生的积极思考中一一猎获，而且也使课堂气氛更加活跃，课堂结构更趋合理。

综上所述，扩散思维不但让学生在习题的解答中初尝成功的滋味，而且使教师在习题的教学中体验授人以渔的喜悦。扩散思维在“一题多解”型习题教学中大有文章可作。