基于PFC2D的断续岩桥直剪强度特征及能量演化机制研究

王雅婷，崔 精

(中交第二公路勘察设计研究院有限公司， 湖北 武汉 430056)

断续节理岩体是水利、采矿、边坡等工程中广泛存在的一类复杂工程介质。与贯通节理岩体相比，断续岩桥的存在使得岩体的受力状态和破坏特征均发生变化，其受力后的破坏特征变相为由原生节理面和自原生节理面端部扩展的岩桥断面所组成的复合破坏面[1]。断续节理的岩体的力学特性对工程安全具有重要意义，也一直是国内外的研究热点。

Lajtai[2-3]最早用节理石膏试样进行直剪试验，提出了岩桥贯通破坏的3种模式，即张拉、剪切和挤压破坏。刘远明等[4-6]总结了共面闭合非贯通节理岩体的破坏机制，并建立了非贯通节理岩体贯通破坏的强度准则。胡波等[7]以摩尔-库仑准则为基础，研究了断续节理岩体抗剪强度的变化规律。张黎明等[8]通过室内模型试验研究共面断续岩桥连通率对岩石抗剪性能的影响。张国峰等[9]通过开展室内常规直剪试验，研究不同宽度岩桥节理岩体的破坏特性和抗剪强度的变化规律。

近年来，基于离散元法的颗粒流程序(Particle Flow Code，PFC)因其能够模拟岩石大变形、非连续等问题，且不涉及宏观本构模型的选取等优点而在岩石的数值模拟中得到迅速的推广和应用[10-13]。如：Huang等[10]利用PFC研究了不同岩桥贯通模式下岩质边坡的破坏形式；Wong等[11]系统地研究了预制裂隙的长度和倾角对裂纹扩展模式的影响。

鉴于颗粒流模拟方法的优势，本文采用PFC2D，考虑连通率和法向应力的影响，研究断续岩桥直剪试验下的强度特性，并结合能量原理分析岩石在变形破坏过程中的能量演化规律。研究成果可为含断续节理岩体的稳定性评价和加固设计提供参考。

1 数值模型的建立

1.1 接触模型及细观参数的选取

在颗粒流程序的接触模型中，平行黏结模型(如图1所示)具有抗拉伸、剪切和力矩效应及黏结破坏-材料宏观刚度劣化的特点，更适合于模拟岩石材料[14]。而对于断续节理面，拟采用光滑节理模型来模拟，其颗粒可实现沿结构面的滑动，有效避免了颗粒间的“颠簸效应”[15]。

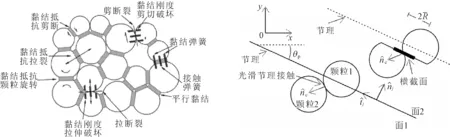
图1平行黏结模型和光滑节理模型示意图[14-15]

PFC中的微观参数与材料的宏观物理力学参数没有直接联系，需建立相应的数值模型，采用“试错法”反复改变细观参数，直到数值模拟试验得到的宏观参数与实际岩石材料主要物理力学参数接近。本文选用的灰岩[16]力学参数见表1，最终确定的微观力学参数见表2。另外，经数值直剪试验获得贯通节理面的抗剪强度参数为：摩擦角21.9°，黏聚力39.4 kPa。

1.2 直剪盒模型构建及计算方案

建立10 cm×7 cm的二维直剪模型，如图2所示。1#、3#、4#墙体组成上剪切盒，2#、5#、6#墙体组成下剪切盒；模型的1#、2#墙体通过伺服控制保持恒定的法向压力；3#、4#墙体保持恒定的水平向右的加载

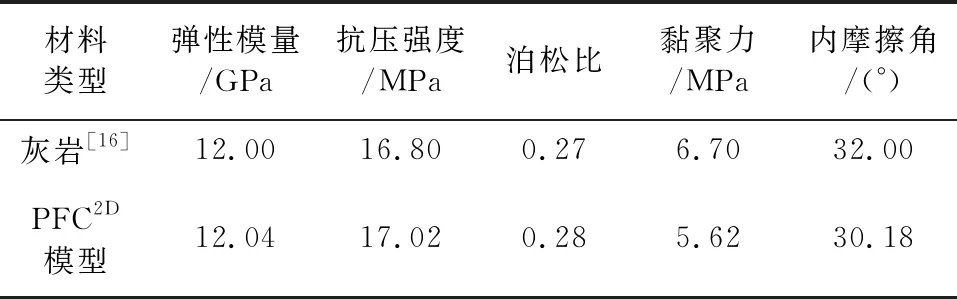
表1 灰岩及PFC2D模型的力学参数

表2 PFC2D模型细观参数

速率，5#、6#墙体保持大小相等、方向相反的加载速率，并以上、下剪切盒的相对水平位移作为试件的剪切位移；同时以3#、4#墙体或5#、6#墙体受到的水平方向的不平衡力除以剪切面的水平投影面积作为平均剪切应力[17]，当试件的剪切位移达到预设值时停止剪切。试件的剪切加载速率最终确定为0.01 m/s，以保证试件始终处于准静态平衡状态。

图2岩石节理直剪试验PFC2D数值模型

采用逐步膨胀法在剪切盒内生成给定半径生成球颗粒，消除浮子后，赋予表1中的平行黏结模型微观力学参数。节理连通率是反应结构面贯通程度的重要参数，其定义为沿结构面的延伸方向上，结构面各段长度与测线长度比值，如图2所示，设计断续节理的连通率k分别为0.30、0.45、0.60和0.75，在颗粒体模型中部生成3条水平共面断续节理，并赋予表2中光滑理模型微观参数。分别在1.0 MPa、3.0 MPa、5.0 MPa、7.0 MPa和9.0 MPa法向应力σn下对4组不同连通率的断续节理岩体进行直剪模拟。

2 岩体直剪强度特性分析

2.1 典型剪切应力-应变曲线分析

不同节理连通率的断续节理岩体在不同法向应力下的剪切应力-应变曲线(剪应变定义为上、下剪切盒的相对位移与原试件沿剪切方向长度比值)大体相似，选取如图3所示的典型曲线(k=0.45、σn=3 MPa)分析。

由图3可见，非贯通节理岩体直剪过程具有明显的阶段性：A阶段为线弹性阶段，该阶段剪切应力曲线呈微向上凸状，剪切应力随剪应变增加而迅速增加，该阶段试件处于线弹性阶段，无裂纹的产生；B阶段为裂纹稳定扩展阶段，该阶段剪切应力去曲线近似呈直线状，剪切应力随剪应变增加而增加，此阶段观察到原生节理面端部开始产生初始张拉性倾斜裂纹，并缓慢扩展(如图4(a)所示)，裂纹数目呈线性增加，定义该阶段初始裂纹产生时的剪切强度为初裂强度τT[18]；C阶段为裂纹不稳定扩展阶段，该阶段剪切应力随剪应变增加而增加，但增速明显减小，直至试件达到剪切峰值强度τm，该阶段裂纹不稳定扩展，裂纹数目迅速增加，且该阶段剪裂纹大量出现(如图4(b)所示)；D阶段为摩擦阶段，该阶段剪切应力曲线呈下凹状，剪切应力随剪应变的增加先迅速降低，后逐渐趋于稳定，上、下试件逐渐错开，该阶段裂纹数量增加速度逐渐减缓直至趋于稳定。由此可知，剪切应力曲线各阶段的变化性与裂纹的扩展密不可分。

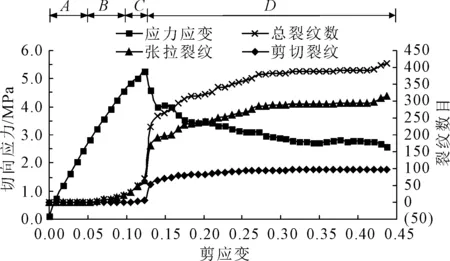
图3 非贯通节理岩体切向变形曲线(k =0.45、σn =3 MPa)

图4 断续节理岩体岩桥的破坏贯通

2.2 剪切强度特性分析

连通率k为0.30、0.45、0.60、0.75的断续节理岩体在1.0 MPa、3.0 MPa、5.0 MPa、7.0 MPa、9.0 MPa法向应力σn下的峰值强度τm和初裂强度τT分别见表3和表4。

由表3可知，断续节理岩体剪切峰值强度随着法向应力的增加而增加；在相同法向应力下，随着节理连通率的增加，剪切峰值强度降低。由表4可知，断续岩桥的初裂强度随法向应力的增加而增加，随节理连通率的增加而降低，这一特性与剪切峰值强度类似。

将初裂强度与峰值强度的比值定义为初裂强度百分比[18]，整理得到表5，由表5可知：在5级法向应力下，节理连通率0.30、0.45、0.60、0.75的断续岩桥初裂强度百分比分别为48.20%～51.83%、49.70%～56.20%、57.62%～62.71%、62.33%～77.19%。在同一节理连通率工况下，初裂强度百分比对法向应力的变化不敏感；随着节理连通率的增加，初裂强度百分比增大。

表3 不同法向应力下断续节理岩体峰值强度

表4 不同法向应力下非贯通节理岩体初裂强度

表5 不同法向应力下初裂强度百分比

3 岩体应变能及耗散能的演化

物质的破坏是能量驱动下的一种失稳状态，岩体在受荷载变形破坏过程中，外界输入的能量转化为岩体的弹性应变能、耗散能、动能以及以热辐射、热交换等形式释放的能量[19-20]。其中，以热辐射或热交换等形式释放的能量可忽略不计，由于体系处于准静态平衡状态，所以动能也可忽略不计，因此本次主要研究岩体外部输入的总能量(边界能)U、内部弹性应变能Ue以及耗散能Ud间的演变。本研究的弹性应变能是模型体在外荷载作用下产生弹性变形而累计的能量，包括颗粒的应变能和平行黏结的应变能2部分，耗散能主要为颗粒间摩擦所消耗的的能量、阻尼能以及裂纹的表面能，可认为Ud=U-Ue。

各工况下断续节理岩体边界能、弹性应变能及耗散能的能量演化大体类似，以k=0.45、σn=3 MPa工况为例具体说明。由图5可知：应力应变曲线与总输入能量曲线、应变能曲线以及耗散能曲线具有对应性；节理岩体达到剪切强度峰值前，随着剪应变的增加能量曲线均增长，且总能及应变能能量曲线均为下凹型，表明增加速率逐渐变大，耗散能曲线缓慢增长，该过程能量主要消耗在原生节理的相对滑动和岩桥尚未贯通破坏前已开裂部分的相对滑动；岩体达到剪切峰值强度后，应变能迅速降低并逐渐稳定，耗散能在峰值强度附近产生“台阶式”增加后稳定增长，形成该现象的原因是该阶段试件发生贯通，产生大量裂纹，能量以表面能形式释放，最终应变能保持稳定，总输入能量和耗散能保持相同速率的稳定增长，外部输入的能量为上、下试件摩擦所耗散；从耗散能的曲线变化可将断续节理岩体的破坏看作是渐进式的。

图5变形过程能量演化曲线(k=0.45、σn=3MPa)

图6为同一节理连通率(k=0.45)不同法向应力条件下和同一法向应力(σn=3 MPa)不同节理连通率条件下耗散能的演化曲线。由图6(a)可知，在不同法向应力条件下，同一连通率节理岩体的能量耗散曲线形态大体相似；岩体未到达剪切强度峰值前，耗散能增长缓慢；在峰值强度时刻，能量发生“台阶式”增长，这种变化在较低法向压力下较为明显；岩体达到峰值剪切强度后，耗散能稳定增长，且与法向应力呈正相关，随着法向应力增加，耗散能越大。由图6(b)可知，同一法向应力下，随着节理连通的增加，耗散能量增加；岩体到达剪切强度峰值时，耗散能曲线形态略有差异，在节理连通率较低时，耗散能呈明显的“台阶式”增长，而当连通率k=0.75时这种现象不明显；总体说来节理连通率造成的耗散能的差异性没有法向应力的明显，如：剪应变为0.45%左右时，同一连通率不同法向应力下耗散能范围变化在20.14 J～110.70 J之间，而同一法向应力不同连通率工况下的耗散能变化范围在31.32 J～46.97 J之间，同时也表明耗散能对法向应力的变化更为敏感。

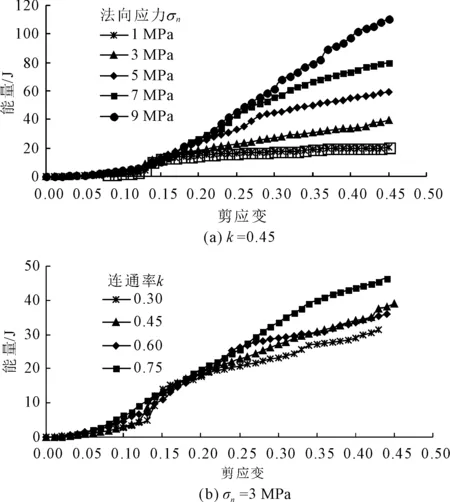
图6耗散能演化曲线

4 结 论

(1) 不同连通率的断续节理岩体直剪破坏过程具有明显的阶段性，可根据剪切应力-应变曲线以及微观裂纹的扩展特征将其分为线弹性阶段、裂纹稳定扩展阶段、裂纹不稳定扩展阶段及摩擦阶段。

(2) 断续岩桥的初裂强度和剪切强度均随法向应力的增加而增加，随节理连通率的增加而降低；初裂强度百分比对法向应力的变化不敏感，而与节理连通率成正相关。

(3) 岩体内部弹性应变能、耗散能的演化与断续岩桥贯通破坏过程相对应，可将弹性应变能下降点或耗散能的“台阶式”增长点看作断续岩桥达到剪切峰值强度的标志；耗散能对法向应力的变化较节理连通率更为敏感。