粒度对非饱和土土水特征曲线滞回特性的影响
郑 方,刘奉银,2,王 磊
(1.西安理工大学 岩土工程研究所,陕西 西安 710048;2.陕西省黄土力学与工程重点实验室,陕西 西安 710048;3.陕西铁路工程职业技术学院, 陕西 渭南 714000)
对非饱和土土水特征曲线有关特性进行研究,有助于解决工程实际中遇到的非饱和土相关问题[1]。Kawai等[2]、Vanapalli等[3]、Ng等[4]、王铁行等[5]、张雪东等[6]、宋亚亚等[7]、苗强强等[8]、刘锦程等[9]分别从不同方面对土水特征曲线的影响因素进行了研究,表明孔隙比、初始含水率、初始干密度、应力历史、温度、干湿循环次数等都对土水特征曲线有一定程度的影响。但是研究不同粒度对土水特征曲线的影响较少,因此,有必要进行研究。
Gallage等[10]和Yang等[11]提出使用“滞回圈面积”来量化土水特征曲线滞回水平的大小,滞回圈面积是一个绝对大小值,但它受吸力路径、试验范围的影响,且“滞回圈”面积不能用以表示不同土之间土水特征曲线的滞回水平的大小。因此,刘奉银等[12]提出了“滞回度”的概念,反映的是在一定体积含水率范围内,一个土试样发生滞回的能力。“滞回度”是一个相对值,不受吸力路径、实验条件的限制,且可以用来描述不同土类土水特征曲线滞回水平的强弱。
基于此,本文利用GCTS土-水特征曲线仪对西安黄土、青藏黏土、新疆黄土进行增-减湿循环试验,得到这三种土的增减湿土水特征曲线试验数据,并结合已有文献中增减湿试验数据,选取Gardner模型,利用MATLAB对试验数据点进行非线性拟合,得到拟合滞回曲线,然后利用滞回度概念从定量的角度对不同土的滞回水平的大小进行评价。
粒度,从广义上讲,是指土中固体颗粒的成分、大小、级配、形状、粗糙度等诸方面,本文主要从颗粒大小和颗粒级配角度来研究粒度对非饱和土土水特征曲线滞回特性的影响,研究成果有利于我们更好地认识非饱和土的土水特性, 对于与非饱和土相关的工程建设及工程问题具有一定的指导意义。
1 试验方案
1.1 试验仪器
试验仪器为GCTS土-水特征曲线仪,如图1所示。该仪器主要由量测装置、加载装置和压力室组成。压力室底座为一圆形凹槽,用于安放高进气值陶土板,采用环氧树脂将陶土板和配套的环套粘合好,然后嵌入凹槽中,使用O型圈将其内壁密封,凹槽底部刻有蛇形槽,用于冲刷陶土板底部的气泡。记录两根体变管中的水量变化,从而可以计算出试验过程中的试样含水率,体变管的精度为1 mm。试验时认为水量在24 h内变化量小于0.1 ml[13]时吸力平衡。试验具体的操作步骤参照刘奉银等[12]文中所述。

图1 GCTS仪器图
1.2 试验用土
试验用土:西安黄土、青藏黏土、新疆黄土。
西安黄土取于西安市西安理工大学曲江校区;青藏黏土取于冻土工程国家重点实验室青藏高原研究基地西侧200 m处;新疆黄土取自新疆伊犁特克斯县西北部。试样制备依据刘奉银等[14]的方法制备,试样为高3.13 cm,直径7.13 cm的圆柱原状样,含水率控制在15%~18%。试验用土的主要物理性质参数如表1所示。
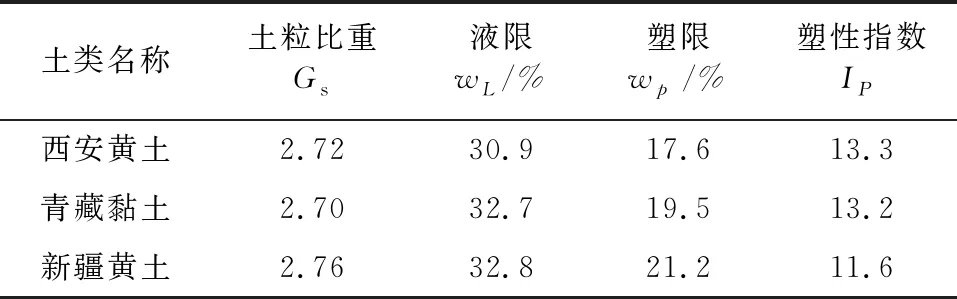
表1 试验用土的主要物理性质参数
1.3 试验方案
对西安黄土、青藏黏土及新疆黄土进行增减湿循环试验,试验方案如表2所示。

表2 西安黄土、青藏黏土和新疆黄土不同土类试样的干湿循环试验方案
具体吸力路径方案为:0 kPa→1 kPa→5 kPa→10 kPa→50 kPa→100 kPa→200 kPa→400 kPa→800 kPa→400 kPa→200 kPa→100 kPa→50 kPa→10 kPa→5 kPa→1 kPa→0 kPa。
2 试验结果分析
2.1 滞回度的概念
刘奉银等[12]提出滞回度的概念,能够反映出在一定体积含水率范围内,试样发生滞回的水平。滞回度的定义为:在一个增-减湿循环过程中,相同的吸力值下,对应的减湿和增湿过程中体积含水率的最大差值与其饱和体积含水率和残余体积含水率差值的比值。
滞回度的具体表达式为:
(1)
式中:Dd/w为土水特征曲线的滞回度;Δθmax为滞回曲线上相同吸力值对应的减湿与增湿过程中体积含水率的最大差值;θs为减湿过程对应的饱和体积含水率;θr为减湿过程对应的残余体积含水率。
滞回度在定量上评价土水特征曲线滞回水平上较有优势。且“滞回度”求取过程更容易而且误差较小,滞回度值的精确度取决于土水特征曲线的拟合精度,而目前较为常用的几个土水特征模型,如:Gardner模型[15],Fredlund-Xing模型[16],Van Genuchten模型[17]等,拟合精度都较高,而“滞回圈面积”需要受制于土水特征曲线是否可积,近似求取的误差相对较大。
2.2 颗粒大小及颗粒级配对土水持水曲线滞回特性的影响
(1) 不同土的颗粒组成。为了研究粒度对土水特征曲线的影响,从颗粒组成角度对不同土类进行分析,先对西安黄土、青藏黏土、新疆黄土做了颗分试验,并引用全风化火山土[4]、全风化凝灰岩[18]和泾阳黄土[19]的试验数据进行对比,图2为六种土的粒径级配累积曲线。
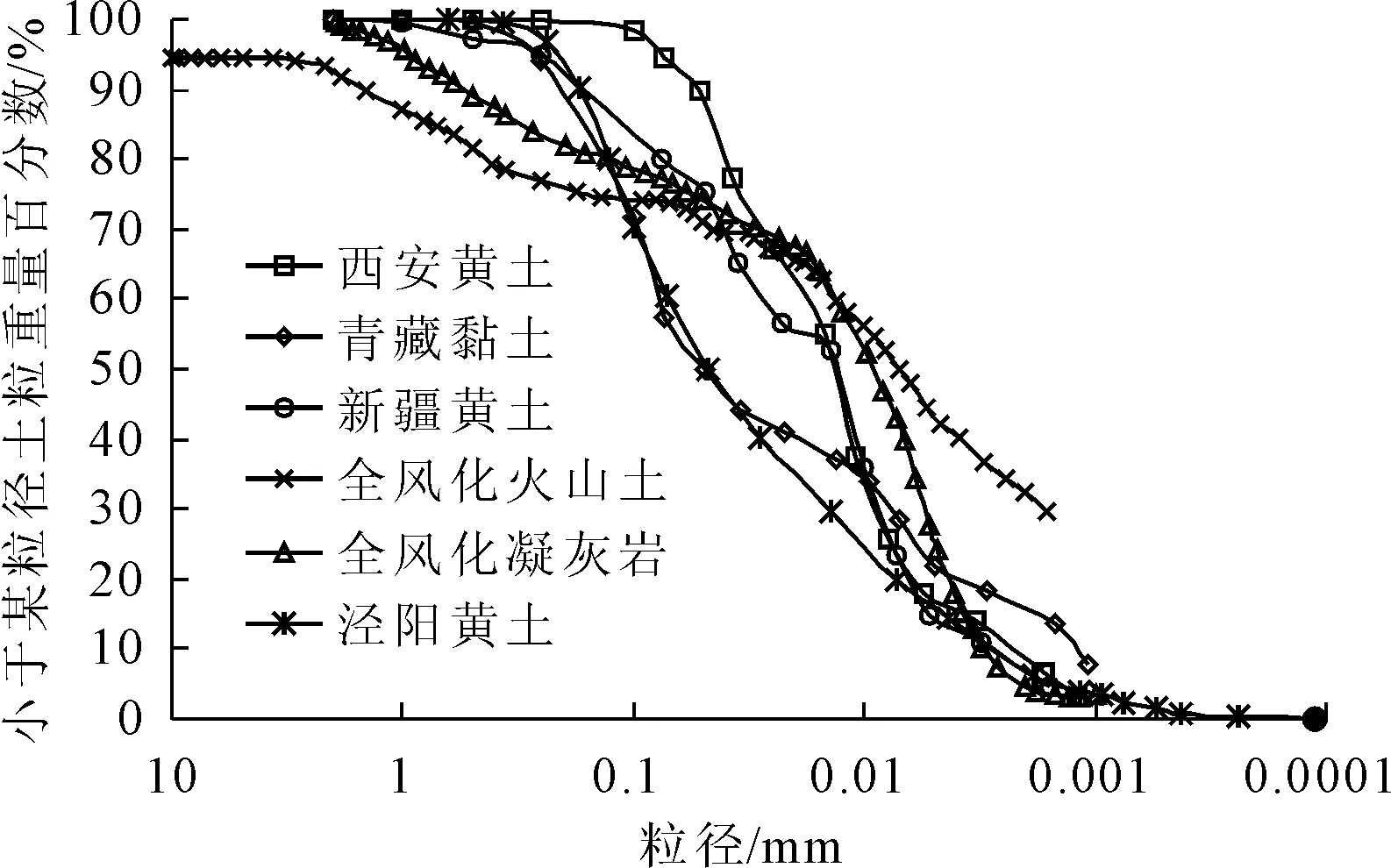
图2 粒径级配累积曲线
根据图2中的粒径级配曲线,计算得出这六种土的不均匀系数Cu和曲率系数Cc,如表3所示,其颗粒组成如表4所示。
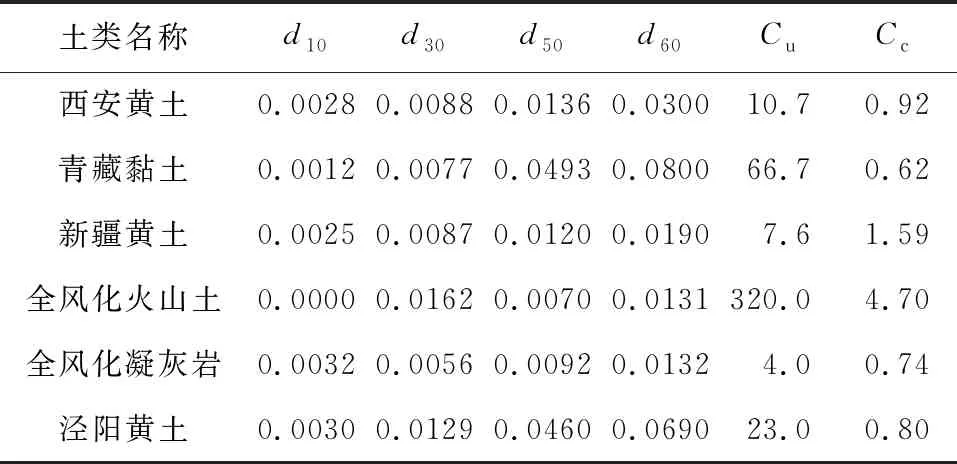
表3 不均匀系数与曲率系数
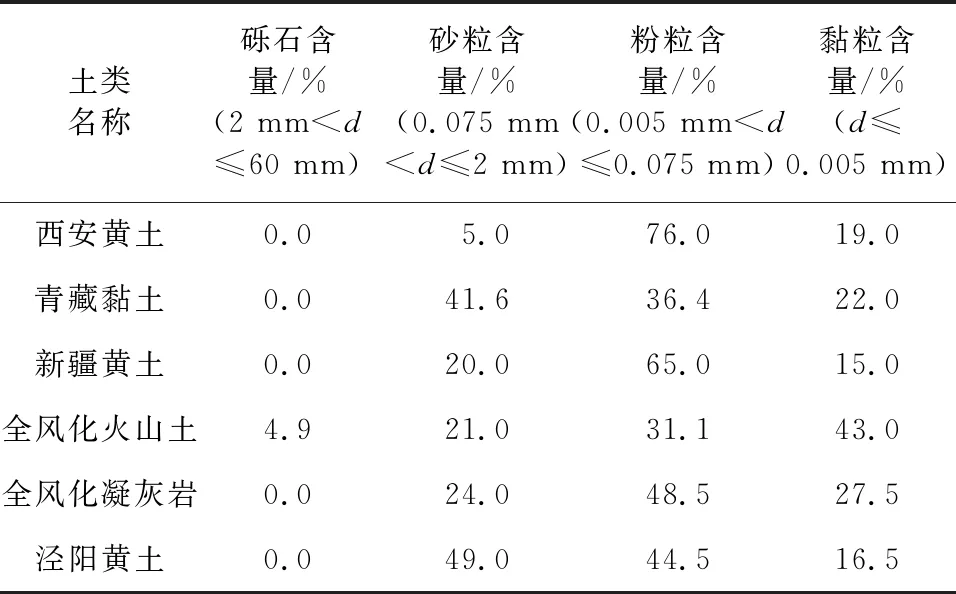
表4 六种土的颗粒组成
(2) 六种土的滞回曲线。选取Gardner模型[15]:
(2)
式中:θr为残余体积含水率;a为与进气值相关的参数;n为基质吸力大于进气值后与土体减湿速率相关的参数。
使用MATLAB中lsqucurvefit拟合函数进行非线性曲线拟合[20],得到相对应的拟合参数及拟合曲线。表5为西安黄土、青藏黏土、新疆黄土、全风化火山土[4]、全风化凝灰岩[18]、泾阳黄土[19]的拟合参数统计表, 图3为各种土的土水特征曲线实测数据和Gardner模型拟合曲线。
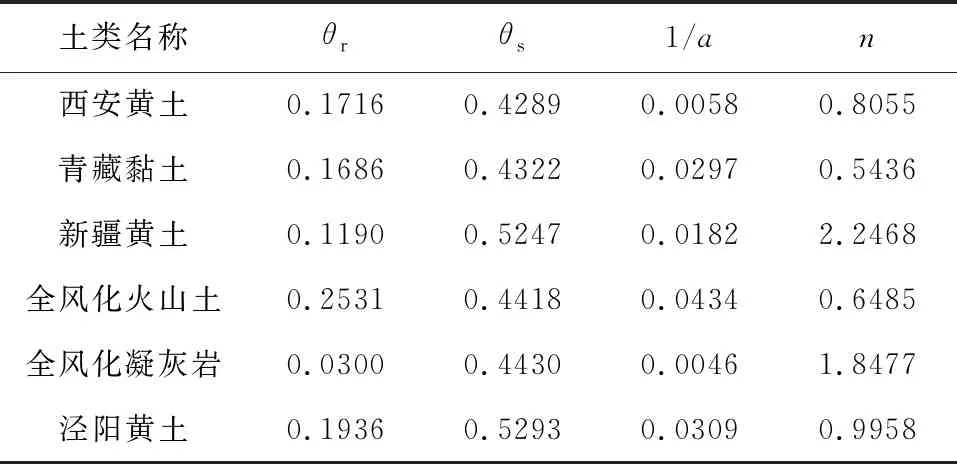
表5 Gardner模型拟合参数表

图3 六种土的SWCC滞回曲线
由图3看出该六种土的土水特征曲线都有明显的滞回特性,为了定量研究其滞回特性,计算其滞回度值,结果见表6。

表6 滞回度值统计表
分析六种土的土水特征曲线的滞回度值规律,发现各个土的滞回度值与有效粒径d10及不均匀系数Cu之间存在一定的关系,绘出其变化趋势线,见图4、图5,由图4滞回度值与有效粒径的d10的变化关系可以看出,变化趋势基本上为有效粒径d10越大滞回度值越大,由图5滞回度值与不均匀系数Cu的变化关系可以看出,变化趋势基本为Cu越大滞回度值越小。

图4 滞回度值Dd/w与有效粒径d10的变化

图5 滞回度值Dd/w与不均匀系数Cu的变化
2.3 原因分析
从瓶颈效应[21]和接触角[22]两个方面上来分析粒度对滞回度的影响。
(1) 瓶颈效应是引起土水滞回特性的重要原因,从基质吸力与表面张力的关系式(3)及瓶颈效应的示意图图6来进行分析。
基质吸力与表面张力的关系式:
(3)
式中:ψ表示基质吸力;Rs表示毛细管半径;Ts表示毛细管弯液面的表面张力;α表示弯液面与毛细管壁的接触角。
土颗粒间存在有一系列细小且不规则的孔隙通道,用图6来示意,r和R表示孔隙半径。图6表示增湿、减湿过程孔隙通道内水位的变化,假设α=0,当水位高度为hw时,ψw=2Ts/r,当水位高度为hd时,ψd=2Ts/r,当ψw=ψd,当hw 图6 瓶颈效应示意图 颗粒分布越不均匀,颗粒间大小颗粒可以相互填充,如全风化火山土的颗粒分布最不均匀,但粘粒含量达到了43%,这部分细小的颗粒能够充分有效地填充土体内部大颗粒之间的大孔隙,导致土体内部的孔隙尺寸较小,即r和R较小,相同吸力条件下,增湿与减湿过程土体内持有的水量差异较小,土水特征曲线的滞回水平就相对较弱。 (2) 图7为接触角效应示意图,αw、αd分别为增湿端、减湿端与斜坡面的接触角,增湿端对应水流流向,减湿端对应水流方向的反向,αw>αd,类似地,增减湿过程中弯液面与土颗粒间的接触角,可看做是减湿端、增湿端液面与坡面的接触角,显然增湿过程中接触角要大于减湿过程中的,从而引起增减湿过程中土体内持水量差异,发生滞回现象。 由式(3)可知,当Rs减小时,对应的吸力值ψ增大,对于内部孔隙尺寸较小的土,土水特性对其敏感程度相对较小,从而接触角的影响相对较弱,因而土水特征曲线滞回水平较弱。而当土颗粒的有效粒径d10越大,最小颗粒的粒径越大,能填充大颗粒间的小颗粒就越少,颗粒间的孔隙通道越大,土水特征曲线滞回水平就越强。 图7 接触角示意图 总而言之,有效粒径d10越大,最小颗粒的粒径越大,能填充大颗粒间的小颗粒就越少,颗粒间的孔隙通道越大。不均匀系数Cu越大,颗粒分布越不均匀,颗粒之间可以相互填充,导致土体内部的孔隙尺寸较小。有效粒径d10和不均匀系数Cu会影响颗粒间孔隙尺寸大小的差异,从而导致了滞回水平的不同。 (1) 对比不同土的土水特征滞回曲线,利用滞回度值定量表征土水特征曲线滞回水平的大小,从颗粒大小和颗粒级配角度研究分析了粒度对非饱和土土水特征曲线滞回特性的影响,结果表明,有效粒径d10越大,滞回水平越强;而土的不均匀系数Cu越大,滞回水平越弱。 (2) 首次尝试利用滞回度值来定量对比不同土、不同吸力路径土的土水特征曲线能力的强弱,将滞回度值进行了应用,并为对比土类不同、吸力路径不同时如何对比滞回水平的大小提供了新的方法。 (3) 从瓶颈效应和接触角效应角度分析,不同土之间土水特征曲线滞回水平产生差异的原因主要是其固体颗粒间孔隙尺寸大小的不同。

3 结 论

