基于地基LiDAR高度指标的小麦生物量监测研究
邱小雷 方 圆 郭 泰 程 涛 朱 艳 姚 霞
(南京农业大学国家信息农业工程技术中心, 南京 210095)
0 引言
农作物生物量是反映其生长状况的重要指标,是形成作物产量的基础,其大小与作物群体光合利用、环境因子胁迫、产量和品质形成等因素密切相关[1-2],监测作物生物量对作物生产能力估计及田间管理具有重要的意义。传统监测小麦生物量的方法是人工田间采样后测量,不仅具有一定的破坏性,而且工作量大、成本高、耗时长,不能及时反映小麦的生长状况[3]。遥感技术具有快速、动态、无损等优点,应用遥感技术监测小麦生物量的研究也越来越多[3-5]。常规遥感技术多采用被动遥感的方式,通过获取植被光谱信息反演小麦生物量,监测手段包括各种地面光谱仪、无人机影像以及卫星遥感影像等,但是光学遥感对天气条件非常敏感,不利于随时观测[1]。LiDAR是近年来迅速发展起来的一门新技术,与光学遥感技术不同的是,LiDAR是一种主动传感器,不受周围环境光条件限制,具有较强的穿透能力,在植被结构参数获取方面具有显著的优势[6]。
LiDAR在监测森林生物量的研究中已经取得了较好的结果[7-9],估测精度相对较高,但在农作物上的应用还处于起步阶段。WANG等[10]将机载LiDAR数据的派生指标、高光谱影像的植被指数两者相结合,提高了对玉米生物量的估测精度。TILLY等[11]以水稻为对象,基于地基LiDAR构建作物表面模型(CSM),提取植物株高,然后与田间实测作物生物量进行相关分析,建立了基于CSM的生物量回归模型,实现了水稻生物量评估。将LiDAR技术应用于作物生物量监测可以提高估测精度,本文在现有研究基础上,以小麦为对象,地基LiDAR为监测平台,借鉴相关研究方法,扩展试验设计,构建和比较不同的高度指标监测模型,探索估测小麦生物量的方法。
1 材料与方法
1.1 试验设计
试验于2016年10月—2017年6月在国家信息农业工程技术中心如皋试验示范基地(32°15′N,120°38′E)进行。试验选用2个品种:扬麦15(V1)、扬麦16(V2);3个氮肥水平:0 kg/hm2(N0)、150 kg/hm2(N1)、300 kg/hm2(N2);2个密度水平:行距25 cm(D1,2.4×106株/hm2)、行距40 cm(D2,1.5×106株/hm2)。采用随机区组设计,重复3次,共计36个小区,单个小区面积为30 m2(6 m×5 m)。
1.2 数据获取与处理
1.2.1生物量的测定
在小麦的分蘖期、拔节期、抽穗期、开花期、灌浆期各进行1次田间取样,每小区取2行×0.3 m,按植株器官分离,绿色叶片按叶位分离。室内测定时,样品在105°杀青并在80°干燥后称量,得到植株不同部位器官质量以及绿色叶片的总干质量,进而计算得到关键生育期各小区单位土地面积干物质量。
1.2.2高度指标的获取
在小麦关键生育期田间取样的同时,利用RIEGL-VZ 1000型地面激光雷达(图1)获取小麦植株的点云数据。地基LiDAR采用8站点方案,扫描模式为60模式,即角分辨率为0.06°,每转过0.06°获取一次点数据,站点方案见图2。

图1 地基LiDAR田间测试图(仪器架设高度为1.5 m)Fig.1 RIEGL-VZ 1000 LiDAR working diagram in field (height of instrument was 1.5 m)

图2 站点方案示意图Fig.2 Scanner position scheme
使用RiSCAN PRO软件进行小麦植株点云数据预处理,得到地面数字高程模型(Digital elevation model,DEM)和关键生育期的数字表面模型(Digital surface model,DSM),通过差值生成每个生育期的冠层高度模型(Canopy height model,CHM),最后基于IDL语言开发脚本提取高度特征参数[12]。目前在监测植物生物量的研究中,主要使用的高度特征指标有平均值Hmean、最大值Hmax、最小值Hmin、百分位值Hp等[11,13],借鉴前人经验,本文选Hmax、H95、H90、H85、H80、Hmean、Hmin等特征指标作为研究对象。
1.3 研究方法
1.3.1非线性回归
非线性回归是表示输入变量到输出变量之间的曲线函数关系。对于样本数据集T={(x1,y1),(x2,y2),…,(xn,yn)},寻找一条函数曲线f(x),不但能很好地拟合已有样本集数据且对新的数据也能很好地预测[14]。本文采用幂函数方程拟合曲线,该过程即求解回归方程中参数a、b,从而建立模型量化高度指标与小麦生物量的关系,幂函数方程为
f(x)=axb
(1)
1.3.2支持向量回归
支持向量回归(Support vector regression,SVR)是支持向量机(Support vector machine,SVM)在回归应用方面的推广,是一种基于结构风险最小化原则的机器学习算法[15],具有良好的泛化能力,可较好解决小样本下的学习问题,同时因使用核函数将复杂的空间映射计算简单化,能有效处理非线性回归预测问题,已成功地应用于多种植物生物量的预测[16-17]。SVR通过特征空间估计内积的核,隐式地实现输入变量到高维特征空间的映射,然后在高维特征空间中构建线性回归函数,对应原空间非线性问题的求解,其数学模型如下
(2)
式中k(xi+x′)为核函数,ai、a′i有小部分不为0,所对应的样本点称为支持向量。ai-a′i和b通常在拟合中自动优化得到[18]。不同的核函数类型及参数对模型的泛化能力影响较大,常用的核函数有线性核函数、多项式核函数、径向基核函数、Sigmoid核函数,其中高斯径向基核函数(RBF核函数)具有很好的泛化能力, 并且能支持非线性回归,本研究中选取的核函数为RBF核函数,公式为
(3)
式中xi——样本点
x′——核函数中心点
σ——宽度参数,控制了函数的径向作用范围
通过RBF核函数能够将原始空间映射到无穷维空间。本文使用支持向量回归建立小麦生物量监测模型时增加样本中生育期作为新特征维度,将生育期经过one-hot编码预处理后再用于建模和检验。
1.3.3特征选择与模型构建
将5个关键生育期共获取的180组数据每生育期随机抽取3~6组数据,共计20组作为测试集,用于独立检验和评价。剩余160组数据作为建模集,基于十折交叉验证法分别采用幂函数回归与支持向量回归对建模样本进行特征选择、模型训练,构建各算法最优的全生育期小麦生物量监测模型。具体步骤是将建模数据集随机分成10个子集,轮流将其中9个作为训练集,1个作为验证集,首先对Hmax、H95、H90、H85、H80、Hmean、Hmin等特征参数分别迭代10次,用10次结果的平均值作为评分项,选择特征参数;然后将所选特征参数在10次交叉验证结果中的最优值作为模型参数估计,构建监测模型;最后在独立测试集上进行检验和评价,评估模型的泛化能力。
1.3.4模型评价指标
模型评价指标包括决定系数R2、均方根误差(RMSE)和相对均方根误差(RRMSE),计算公式为
(4)
(5)
(6)
式中n——样本数量
Oi——样本i的实测值
Pi——对应样本i的模型预测值


RMSE——均方根误差
RRMSE——相对均方根误差
1.3.5建模工具
基于Python 3.5环境,利用Pandas、Scipy和Sklearn等扩展模块开发所需数据处理、分析建模和检验评价的程序。Scipy模块optimize组件中curve_fit函数可实现曲线拟合,用于构建幂函数回归模型。应用Sklearn模块中model_selection组件的train_test_split切分数据样本集,Sklearn还提供了包括支持向量回归等在内全面的机器学习算法与丰富的调用接口[19]。SVR 算法由Sklearn 模块中的SVM组件实现,影响SVR性能的主要超参数有核函数kernel、惩罚系数C和核系数g,C过大或过小泛化能力变差,g过大易发生欠拟合,反之则可能过拟合,根据经验本文设置惩罚系数C为1 000,核系数g为0.001。
2 结果与分析
2.1 关键生育期数据结果
地基LiDAR点云数据经过点云配准、拼接等预处理后,生成小麦关键生育期的点云图(图3),然后结合地面高程模型,应用IDL脚本提取高度特征参数。小麦地上部生物量经田间取样,室内测定后获得。如图4所示,关键生育期数据结果表明,小麦的高度指标Hmean由分蘖到灌浆随生育进程变化速率由大趋小,地上部生物量变化速率则由小趋大。
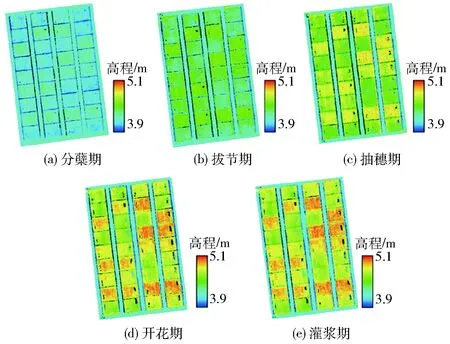
图3 不同生育时期小麦点云图Fig.3 Wheat point clouds diagram in different growth stages
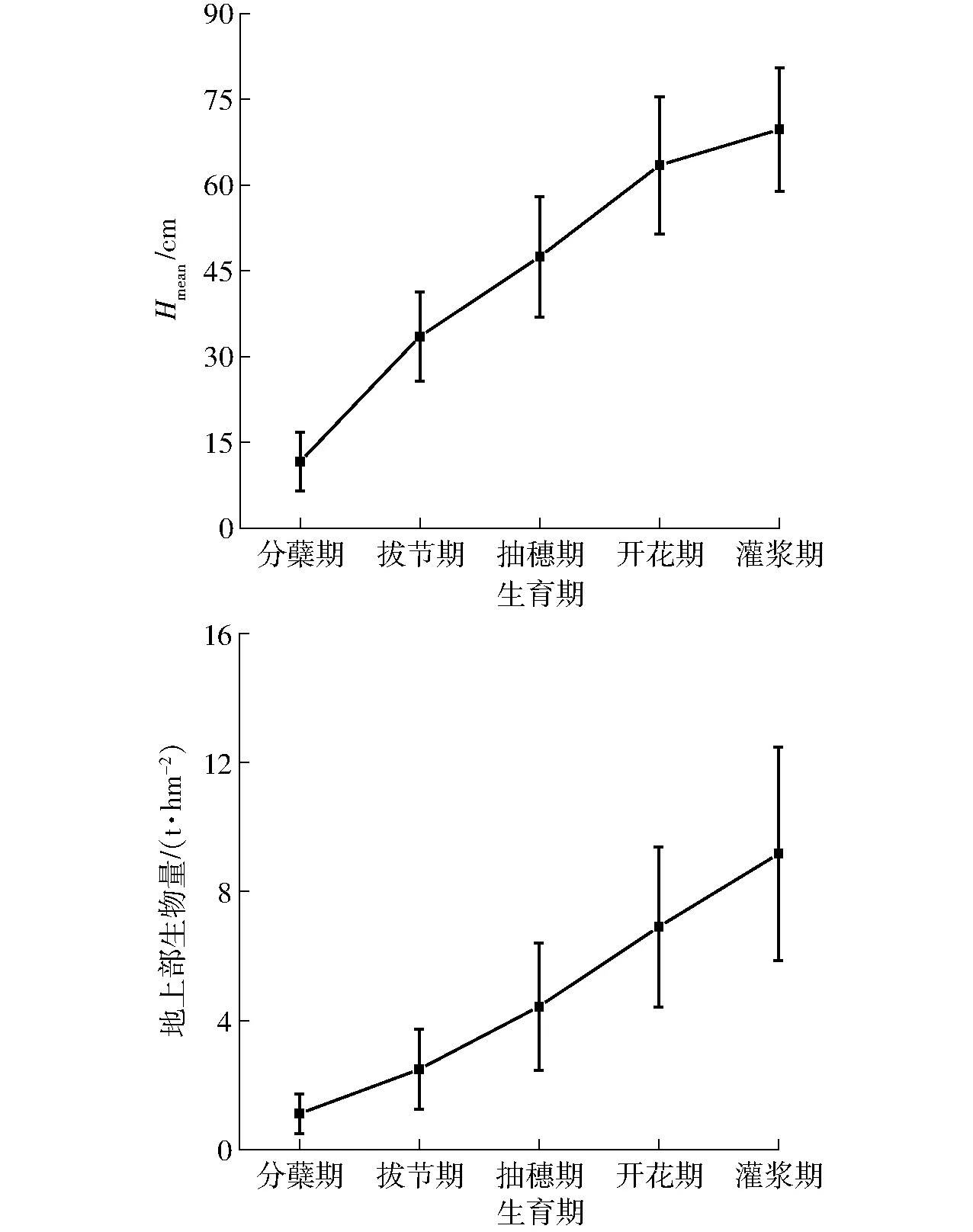
图4 小麦高度指标Hmean和地上部生物量随生育期的变化Fig.4 Variations of height index Hmean and aboveground biomass with growth period of wheat
2.2 高度特征指标选择
利用小麦全生育期试验数据,采用十折交叉检验法,基于幂函数回归与支持向量回归,分别选择高度特征指标用于构建模型。基于幂函数回归模型的验证集上各高度指标10次结果的均值如表1所示,Hmean得分最高,R2=0.805,RMSE为1.439 t/hm2,RRMSE为30.43%,因此构建幂函数回归模型时选择Hmean指标。
基于支持向量回归模型验证集上各高度指标10次结果的均值如表2所示,只使用高度特征指标时Hmean得分最高,R2=0.797,RMSE为1.462 t/hm2,RRMSE为30.82%;增加生育期特征后H95得分最高,R2=0.807,RMSE为1.437 t/hm2,RRMSE为30.31%,且优于单高度指标Hmean,因此构建支持向量回归模型时选择H95与生育期两个特征指标。
2.3 小麦生物量监测模型
选择Hmean指标10次交叉验证结果中的最优值作为模型参数估计,构建全生育期幂函数回归模型,结果如图5所示,幂函数回归模型的决定系数R2为0.809,验证集R2为0.907,RMSE和RRMSE分别为0.887 t/hm2和23.17%。
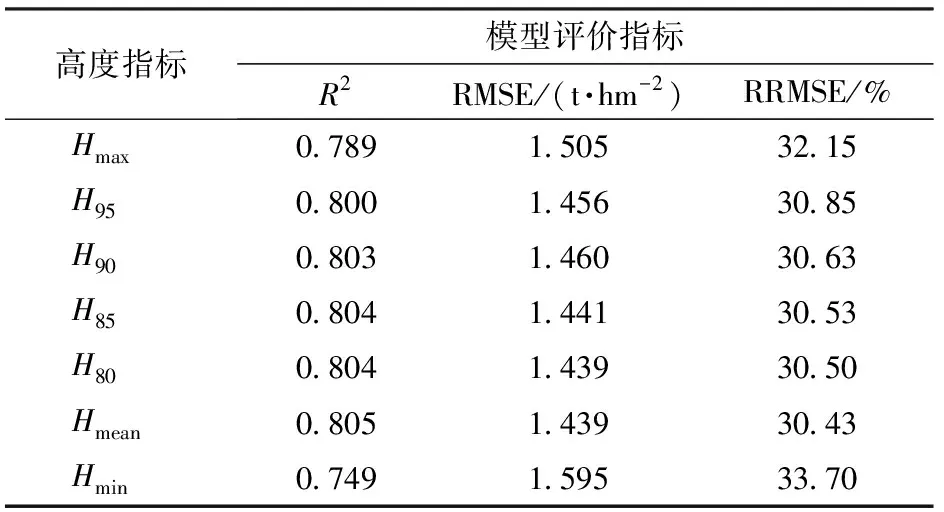
表1 幂函数回归模型高度特征指标结果Tab.1 Results of height characteristic indexes of power function regression model
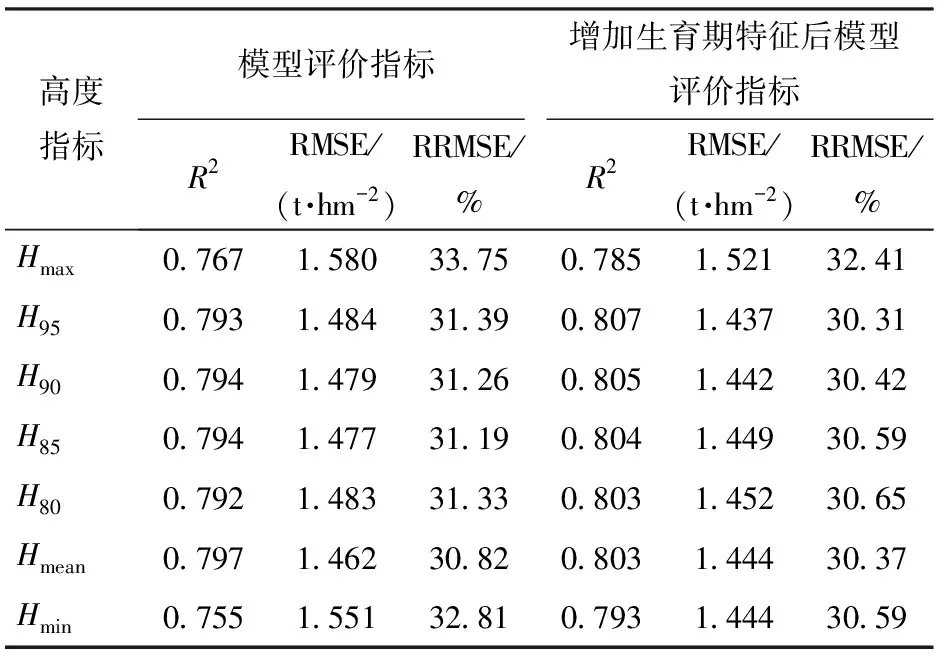
表2 支持向量回归模型特征指标结果Tab.2 Results of feature indexes of support vector regression model
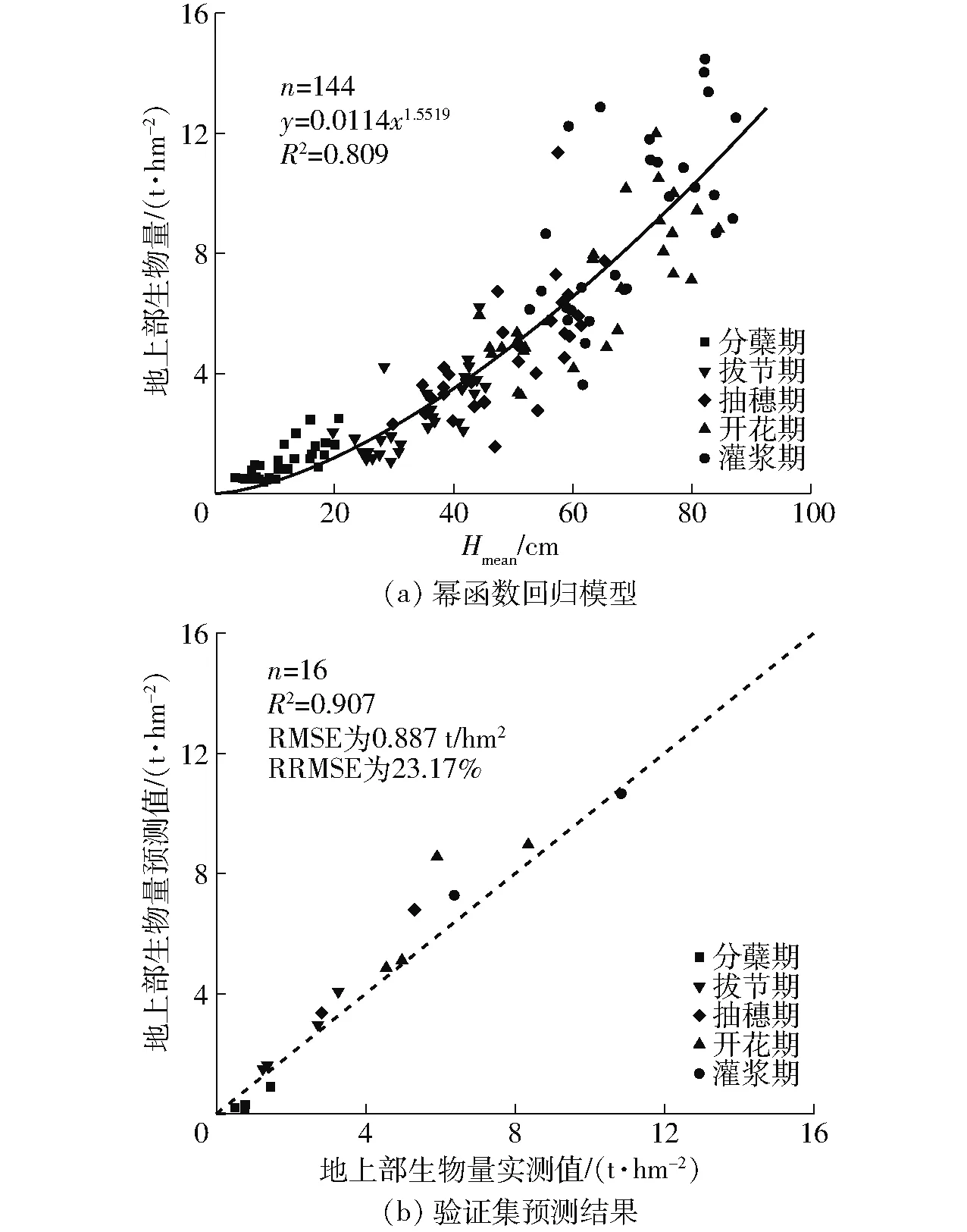
图5 幂函数回归模型构建及验证集的预测结果Fig.5 Establishment of power function regression model and prediction results on verification set
选择H95与生育期两个特征指标在10次交叉验证结果中的最优值作为模型参数估计,构建全生育期支持向量回归模型,模型在建模集上的检验结果如图6所示,其中训练集R2为0.814,RMSE和RRMSE分别为1.492 t/hm2和30.95%,验证集R2为0.919,RMSE和RRMSE分别为0.826 t/hm2和21.59%。
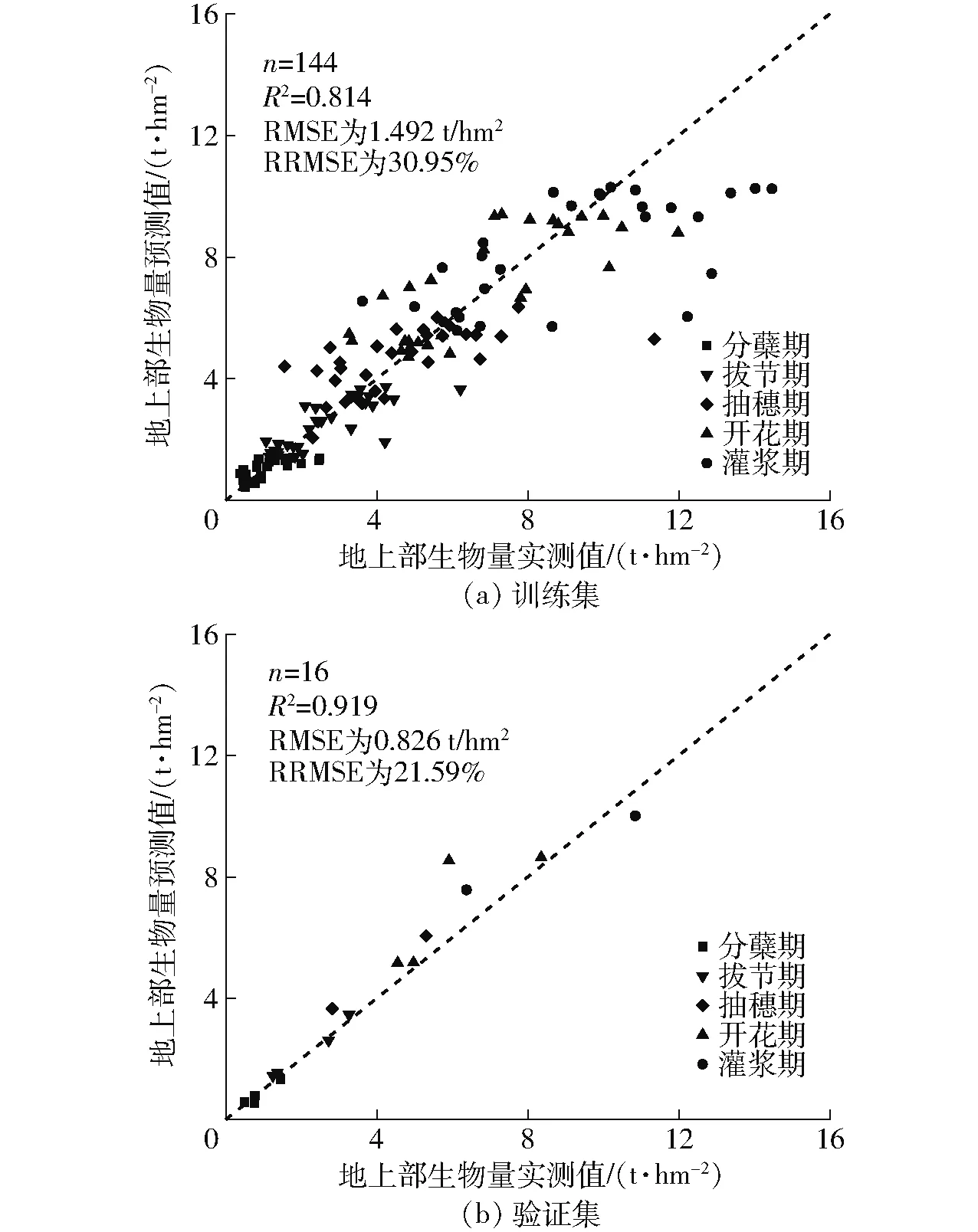
图6 支持向量回归模型训练集和验证集的预测结果Fig.6 Prediction results of support vector regression model on training set and verification set
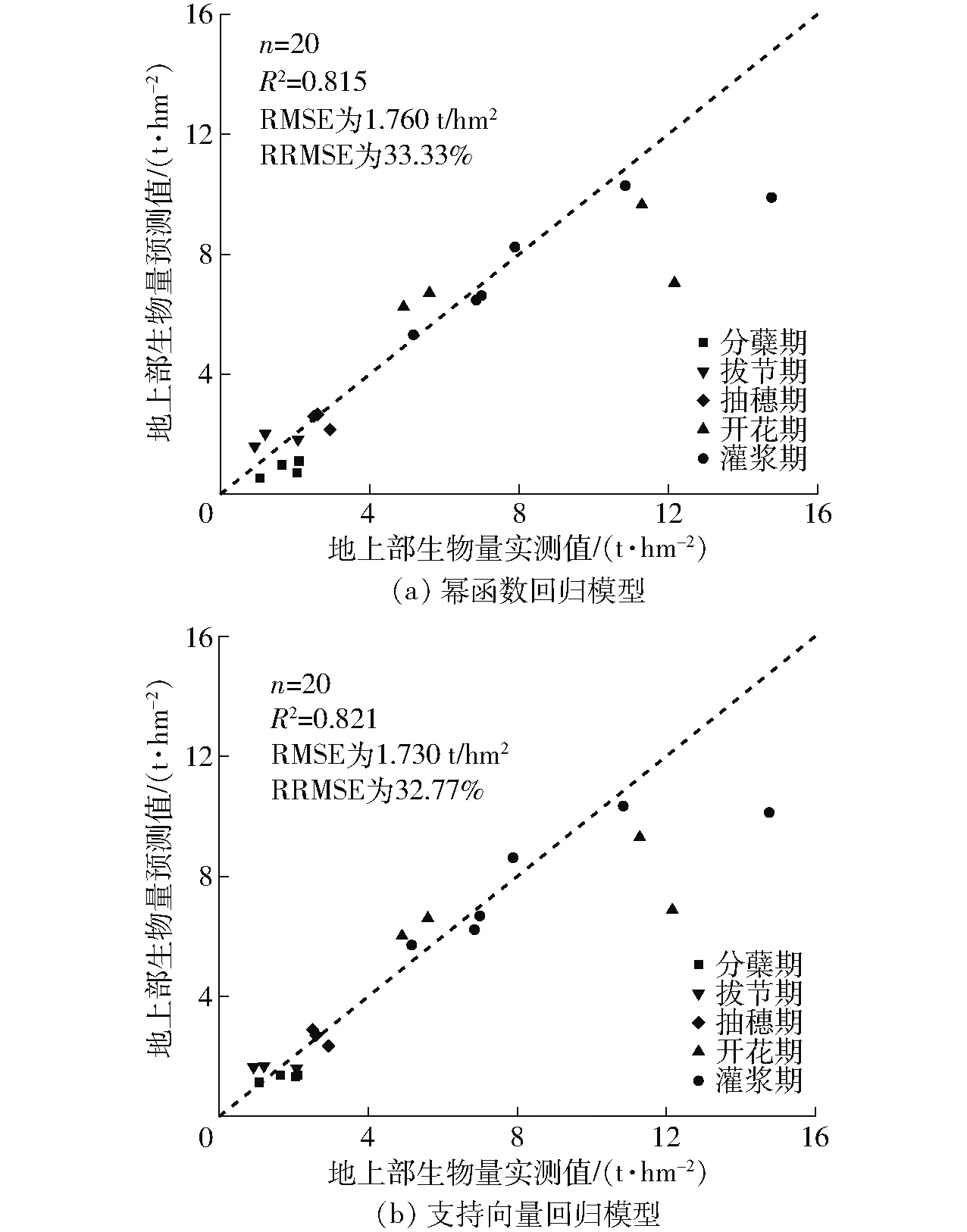
图7 幂函数回归模型和支持向量回归模型测试集的预测结果Fig.7 Prediction results of power function regression model and support vector regression model on test set
2.4 模型评价与比较
已构建的全生育期小麦生物量监测模型在独立测试集上的检验结果如图7所示,幂函数回归模型R2为0.815,RMSE和RRMSE分别为1.760 t/hm2和33.33%,支持向量回归模型R2为0.821,RMSE和RRMSE分别为1.730 t/hm2和32.77%。结果表明,应用地基LiDAR高度指标监测小麦生物量时,增加生育期特征的支持向量回归模型略优于只使用高度指标的幂函数回归模型。但随着小麦生物量的增长,两模型的预测精度明显下降,均出现饱和,一方面这是由于从开花期到灌浆期小麦穗持续增长,进而生物量也随之增长,但是小麦的株高变化不大,从而造成生育后期的低估现象,另一方面可能是因为高密度高氮肥田块与正常田块相比生育后期株高基本一致,但群体较大,高度指标监测模型尚无法准确预测这部分田块小麦地上部生物量。
3 讨论
3.1 不同高度指标监测小麦生物量的结果
LiDAR通过发射激光和接收返回信号的方式,可以获取高精度的植被空间结构信息与冠层底部地形信息[20-21],因此可以快速地估算出小麦的高度特征,进而反演出生物量。现有的研究大部分都利用不同的高度指标来反演生物量,包括Hmax、H95、H90、H85、H80、Hmean、Hstd、Hcv等[22-24]。本文选取高度指标Hmax、H95、H90、H85、H80、Hmean、Hmin,通过十折交叉验证法分别利用幂函数回归与支持向量回归选择特征指标,比较了不同高度指标估测小麦生物量的精度。结果表明,采用幂函数回归模型时,Hmean的估测效果最好,采用支持向量回归模型时,选择H95与生育期两个特征指标建模效果最好。株高是小麦生长变化的关键特征,虽然幂函数回归模型与单高度特征支持向量回归模型中Hmean的效果最好,但H95、H90、H85和H80均反映株高特征,且在数值上与Hmean差异不大,或为比例关系,因此所建立的生物量监测模型估测精度相差很小。
3.2 高度指标监测模型的预测能力
小麦地上部生物量由绿叶、茎鞘、穗3部分组成,不同器官间的干物质积累与转运随品种、环境条件而异[25]。株高随着叶、茎、穗的生长动态变化,与地上部生物量有着显著正相关关系,图4结果表明开花前小麦随着株高变化地上部生物量呈几何级增长,但是到了生育后期株高生长逐渐趋于停止,而地上部生物量还在不断积累,造成高度指标估测小麦生物量的先天局限性。如图8所示为全样本集上小麦地上部生物量实测值与两个全生育期监测模型预测值的分布,实测值的下四分位数、中位数、上四分位数与监测模型基本一致,最小值与支持向量回归模型一致,与幂函数回归模型稍有差异,但实测最大值与两个监测模型差异明显,当地上部生物量较大时监测模型的预测能力明显不足。地上部生物量小于10 t/hm2的全生育期样本集的幂函数回归模型RMSE为1.098 t/hm2,支持向量回归模型RMSE为0.970 t/hm2,大于10 t/hm2的全生育期样本集两个监测模型RMSE分别为3.611 t/hm2与3.826 t/hm2,95%预测值都被低估。如图9所示,样本按实测值分组后地上部生物量小于10 t/hm2的模型RMSE在1.0 t/hm2左右波动,但是超过10 t/hm2时,预测模型RMSE呈指数增长。
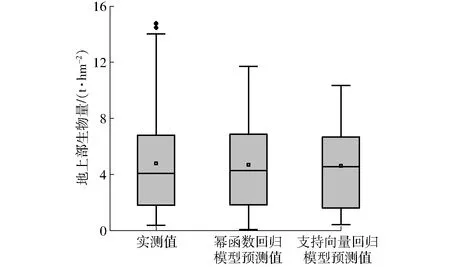
图8 小麦地上部生物量实测值与模型预测值的分布Fig.8 Distribution of measured and predicted aboveground biomass of wheat
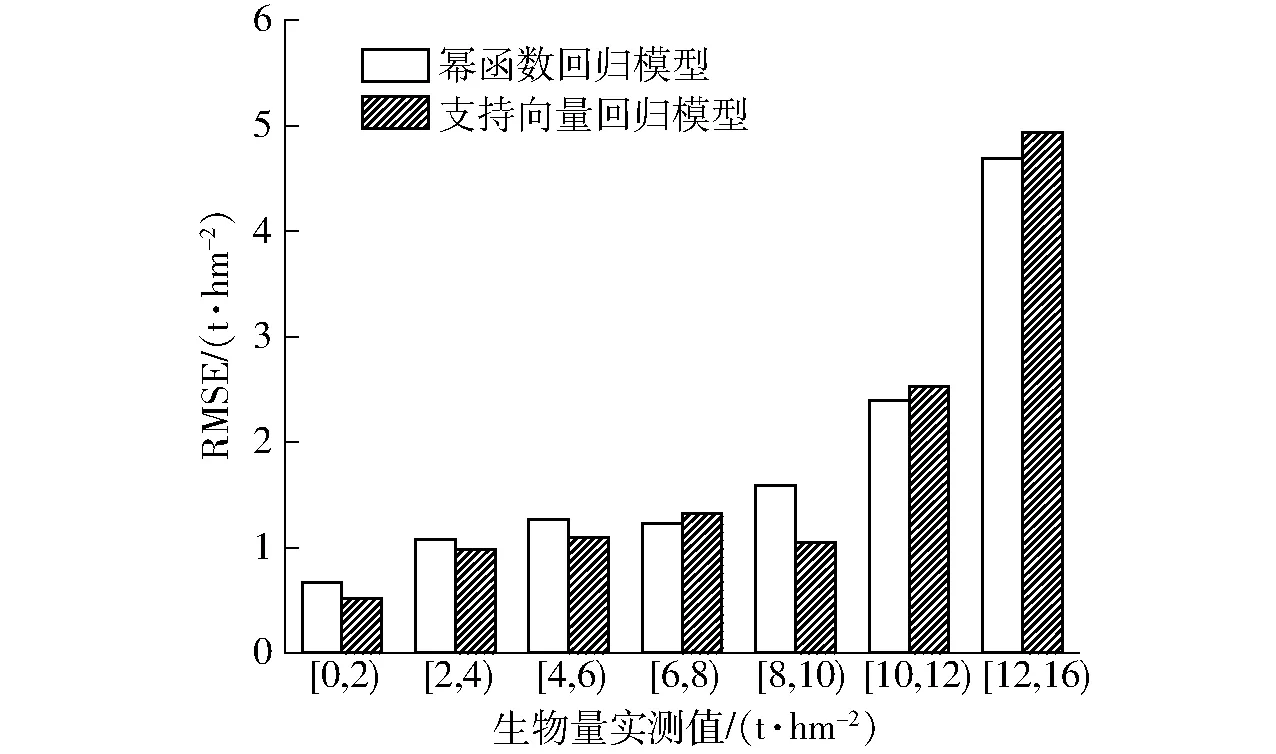
图9 样本按实测生物量分组后RMSE变化图Fig.9 Trend of RMSE after grouping samples according to measured biomass
3.3 生育期特征分析
在单高度指标特征选择的结果中,全生育期幂函数回归模型精度均高于支持向量回归模型,但增加生育期特征后,支持向量回归模型精度得到提升,H95与生育期两个特征指标的得分最高,所构建的监测模型精度也最高。进一步利用建模集中160组样本,基于单个生育期构建Hmean幂函数回归小麦生物量监测模型,并在独立测试集的20组样本上检验。如图10所示,单生育期幂函数回归模型测试集预测结果略优于全生育期构建的幂函数回归模型,但不如支持向量回归模型,生育期特征有利于监测模型预测精度提升。由于小麦不同生育期的形态结构和生理特性具有明显差异,影响了单生育期幂函数回归模型的变化趋势,没有形成一致规律。
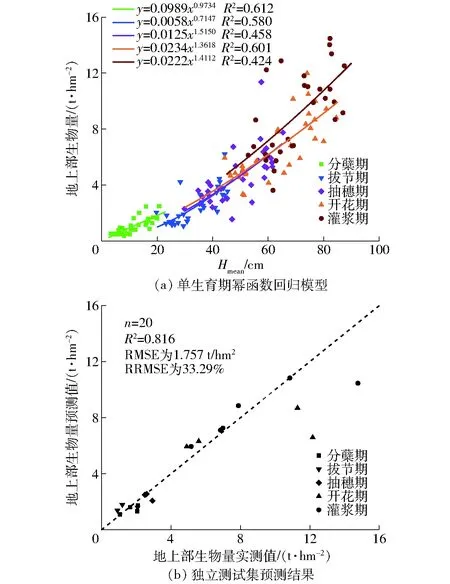
图10 单生育期幂函数回归模型构建及测试集的预测结果Fig.10 Establishment of power function regression model for single growth period and prediction results on test set
3.4 支持向量回归模型的超参数选择
机器学习算法的性能依赖于超参数的选择,支持向量回归模型常用的超参数调试方法有经验凑试法、网格法,以及基于梯度下降算法、遗传算法、粒子群算法的调优方法等[26-28]。由于本文所选的建模特征较少,根据经验设置惩罚系数C为1 000,核系数g为0.001,为了探讨经验值是否合理,以R2为评价指标,迭代计算C的范围为1~5 000,g的范围为0.000 1~0.01,如图11所示,所选经验值分布在高分范围内。
4 结论
(1)利用高度指标Hmean与实测生物量构建全生育期幂函数回归模型,幂函数回归模型决定系数R2为0.809,验证集R2为0.907,RMSE和RRMSE分别为0.887 t/hm2和23.17%,独立测试集幂函数回归模型R2为0.815,RMSE和RRMSE分别为1.760 t/hm2和33.33%。
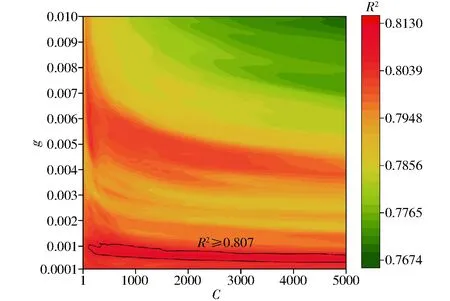
图11 支持向量回归模型超参数评价Fig.11 Superparametric evaluation of support vector regression model
(2)利用H95和生育期两个特征指标与实测生物量构建全生育期支持向量回归模型,训练集模型R2为0.814,RMSE和RRMSE分别为1.492 t/hm2和30.95%,验证集R2为0.919,RMSE和RRMSE分别为0.826 t/hm2和21.59%,独立测试集上R2为0.821,RMSE和RRMSE分别为1.730 t/hm2和32.77%。
(3)由于高度指标估测小麦生物量的先天局限性,两模型较适宜于小麦地上部生物量小于10 t/hm2的情况,当超过10 t/hm2时,样本集上95%模型预测值被低估,RMSE呈指数增长。
(4)基于单生育期构建的幂函数回归模型独立测试集检验结果R2为0.816,RMSE和RRMSE分别为1.757 t/hm2和33.29%,所构建的支持向量回归模型均优于全生育期幂函数回归模型,生育期特征有利于提升监测模型预测精度。

