型仿射Weyl群中aλ,λ′的计算

罗 新，王利萍，魏玉丽

(北京建筑大学 理学院， 北京 100044)

1 预备知识

o(s0s1)=o(s1s2)=o(s2s3)=o(s0s3)=3，
o(s0s2)=o(s1s3)=2.

图型仿射Weyl群的Dynkin图Fig.1 The Dynkin diagram of the affine Weyl

其中，Λ为W0的权格，Λr为W0的根格，则一定存在一个循环子群Ω，使得：

其中，Ω={e,ω,ω2,ω3}，满足：

(a)对于ω：s0ω=ωs1,s1ω=ωs2,s2ω=ωs3,s3ω=ωs0.

(b)对于ω2：s0ω2=ω2s2,s1ω2=ω2s3,s2ω2=ω2s0,s3ω2=ω2s1.

(c)对于ω3：s0ω3=ω3s3,s1ω3=ω3s0,s2ω3=ω3s1,s3ω3=ω3s2.

并且W0={e,s1,s2,s3,s2s1,s3s2s1,s1s2,s3s2,s2s3,s1s2s3,s1s3,s2s1s3,s3s1s2,s2s3s1s2,s1s2s1,s3s1s2s1,s2s3s1s2s1,s2s3s2,s1s2s3s2,s2s1s2s3s2,s2s1s2s3,s3s2s1s2s3,s2s3s2s1,s3s2s1s2s3s2}.

令αi为si对应的单根(i=1,2,3)，则W的正根集为：Φ+={α1,α2,α3,α1+α2,α2+α3,α1+α2+α3}.

设Φ的3个基本支配权[6]为x1,x2,x3，则：

x1=032ω3,x2=0310ω2,x3=012ω.

有Λ=x1+x2+x3，Λ+=x1+x2+x3，Λr=α1+α2+α3.

1.2 和首项系数相关的半线性方程

令v=q1/2，对于y≤w∈W,py,w=vl(y)-l(w)Py,w(v2)∈[v-1]；否则py,w=0. 对于令：

显然，可以得到：当λ=λ′时，bλ,λ′=1；当λ<λ′时，bλ,λ′∈v-1[v-1]，否则bλ,λ′=0.

对于bλ,λ′，可以根据公式μ(mλ,mλ′)=Resv=0(bλ,λ′)计算相应的首项系数，其中Resv=0(f)∈为v-1在f∈A中的系数，而A=是以q为变量的整系数的Laurent多项式环.

显然，可以得到：当λ=λ′时，aλ,λ′=1；当λ<λ′时，aλ,λ′∈v-1[v-1]，否则aλ,λ′=0. 如果不存在子集i⊆R+使得αi=λ，就令Φ(λ)=0.

2 关于aλ,λ′的计算

命题2.1对于A3型仿射Weyl群，有如下的Φ值表：

Φ(0)=1；Φ(α1)=Φ(α2)=Φ(α3)=-v-2；
Φ(α1+α2)=Φ(α2+α3)=-v-2+v-4；
Φ(α1+α2+α3)=-v-2+2v-4-v-6；
Φ(2α1+α2+α3)=Φ(α1+α2+2α3)=v-4-v-6；
Φ(α1+α3)=Φ(2α1+α2)=Φ(α1+2α2)=
Φ(2α2+α3)=Φ(α2+2α3)=v-4；
Φ(α1+2α2+α3)=2v-4-2v-6；
Φ(2α1+2α2+2α3)=-2v-6+2v-8；
Φ(2α1+2α2)=Φ(2α2+2α3)=Φ(2α1+α2+2α3)=
Φ(α1+3α2+α3)=Φ(α1+2α2+3α3)=
Φ(3α1+2α2+α3)=-v-6;
Φ(2α1+2α2+α3)=Φ(α1+2α2+2α3)=
v-4-2v-6+v-8；
Φ(α1+3α2+2α3)=Φ(2α1+3α2+α3)=
-v-6+v-8;
Φ(2α1+3α2+2α3)=-v-6+2v-8-v-10;
Φ(α1+3α2+3α3)=Φ(2α1+4α2+2α3)=
Φ(2α1+2α2+3α3)=Φ(3α1+3α2+α3)=
Φ(3α1+2α2+2α3)=v-8;
Φ(2α1+4α2+3α3)=Φ(3α1+3α2+3α3)=
Φ(3α1+4α2+2α3)=-v-10；
Φ(2α1+3α2+3α3)=Φ(3α1+3α2+2α3)=
v-8-v-10;
Φ(3α1+4α2+3α3)=v-12.

对于其他情形[9]的λ，均有Φ(λ)=0.

X1={λ=4hx1=3hα1+2hα2+hα3|h≥1},
X2={λ=2ix2=iα1+2iα2+iα3|i≥1},
X3={λ=4jx3=jα1+2jα2+3jα3|j≥1},
X4={λ=k(x1+x3)=kα1+kα2+kα3|k≥1},
X5={λ=m(2x1+x2)=2mα1+2mα2+mα3|m≥1},
X6={λ=n(x2+2x3)=nα1+2nα2+2nα3|n≥1}.

其中，h,i,j,k,m,n均为正整数.

定义2.1令λ1=4x1,λ2=2x2,λ3=4x3,λ4=x1+x3,λ5=2x1+x2,λ6=x2+2x3.

命题2.2当λ∈Xi,1≤i≤6，有：

证明：对于W0中的3个单反射，可以分别计算出它们在单根上的作用如下：

s1(α1)=-α1,s1(α2)=α1+α2,s1(α3)=α3.
s2(α1)=α1+α2,s2(α2)=-α2,s2(α3)=α2+α3.
s3(α1)=α1,s3(α2)=α2+α3,s3(α3)=-α3.

设λ=iα1+jα2+kα3，由于W0包括24个群元素，让这些元素依次作用在λ上，得：

e(λ)=iα1+jα2+kα3,
s1(λ)=(-i+j)α1+jα2+kα3,
s2(λ)=iα1+(i-j+k)α2+kα3,
s3(λ)=iα1+jα2+(j-k)α3,
s1s2(λ)=(-j+k)α1+(i-j+k)α2+kα3,
s3s2(λ)=iα1+(i-j+k)α2+(i-j)α3,
s2s3(λ)=iα1+(i-k)α2+(j-k)α3,
s1s2s3(λ)=(-k)α1+(i-k)α2+(j-k)α3
……
s3s2s1s2s3s2(λ)=(-k)α1+(-j)α2+(-i)α3.

□

设λ∈Λr，λ=iα1+jα2+kα3,i,j,k∈；根据α1=2x1-x2,α2=-x1+2x2-x3,α3=-x2+2x3，得：λ=(2i-j)x1+(2j-i-k)x2+(2k-j)x3. 若此时满足λ∈Λ+，则根据x1,x2,x3的系数均大于等于0，得：

综上，i′≤i,j′≤j,k′≤k.

□

□

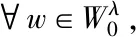
其中，

□

根据命题2.1中Φ值的特征以及命题2.2，可以得到以下命题：

命题2.5设λ=iα1+jα2+kα3，λ′-λ=rα1+sα2+tα3，其中i,j,k≥1；0≤r,t≤3,0≤s≤4, 若w∉{e,s1,s2,s3,s2s1,s1s2,s3s2,s2s3,s1s3,s1s2s1,s2s3s2}，则Φ(λ′+ρ-w(λ+ρ))=0.

证明：对于W0中的24个元素，若w∉{e,s1,s2,s3,s2s1,s1s2,s3s2,s2s3,s1s3,s1s2s1,s2s3s2}，下面只需验证：对于W0中的其余元素，均有Φ(λ′+ρ-w(λ+ρ))=0成立.

当w=s3s2s1时，将其带入到公式：λ′+ρ-w(λ+ρ)=λ′-w(λ)+ρ-w(ρ)中得：λ′-s3s2s1(λ)+ρ-s3s2s1(ρ)=(2i-j+r+1)α1+(i+j-k+s+2)α2+(i+k+t+3)α3. 考虑多项式中α3的系数，由于i+k+t+3≥5，此时显然Φ(λ′+ρ-s3s2s1(λ+ρ))=0.

当w=s1s3s2时，λ′+ρ-w(λ+ρ)=λ′-w(λ)+ρ-w(ρ)=λ′-s1s3s2(λ)+ρ-s1s3s2(ρ)=(i+j-k+r+2)α1+(-i+2j-k+s+1)α2+(-i+j+k+t+2)α3. 把α1和α3的系数相加可得：(i+j-k+r+2)+(-i+j+k+t+2)=2j+r+t+4≥6.

(b)当2j+r+t+4>6时，由于0≤r,t≤3，所以α1和α3的系数之和应小于或等于6，矛盾. 综合(a)和(b)，可得：当w=s1s3s2时，Φ(λ′-s1s3s2(λ)+ρ-s1s3s2(ρ))=0.

同理，当w=s1s2s3,s2s3s1s2,s3s1s2s1,s2s3s1s2s1,s1s2s3s2,s2s1s2s3s2,s2s1s2s3,s3s2s1s2s3,s2s3s2s1,s3s2s1s2s3s2,s2s1s3时，相应的Φ(λ′+ρ-w(λ+ρ))=0.

综合以上分析可得：若w∉{e,s1,s2,s3,s2s1,s1s2,s3s2,s2s3,s1s3,s1s2s1,s2s3s2}，则有Φ(λ′+ρ-w(λ+ρ))=0.

□

(a)当w=s1时，λ′+ρ-s1(λ+ρ)=λ′-s1(λ)+ρ-s1(ρ)=(2i-j-n+1)α1，由上可知：2i-2n-j≥0，即2i-j-n≥n≥2. 所以2i-j-n+1≥3. Φ[(2i-j-n+1)α1]=0.

(b)当w=s2s1时，λ′+ρ-s2s1(λ+ρ)=(2i-j-n+1)α1+(i+j-k-n+2)α2. 因为i+k-2j≤0，得i-j≤j-k，所以i+j-k≥2i-j≥2n，有i+j-k-n+2≥4. 又因为2i-j-n+1≥3，所以Φ[(2i-j-n+1)α1+(i+j-k-n+2)α2]=0.

同理，当w=s2,s3,s1s2,s2s3,s1s3,s1s2s1,s2s3s2时，相应的Φ(λ′+ρ-w(λ+ρ))=0.

综上，根据aλ,λ′的计算公式，可得：当λ′-λ=nα1,n≥2时，aλ,λ′=0.

□

除了定理2.2中的情形，根据命题2.1，可得：当λ′-λ等于以下情况时，aλ,λ′=0.

(a)nα2,(n≥2).

(b)nα3,(n≥2).

(c)iα1+jα3，(i,j)≠(1,1).

(d)iα1+jα2，(i,j)∉{(1,1),(1,2),(2,1),(2,2)}.

(e)iα2+jα3，(i,j)∉{(1,1),(1,2),(2,1),(2,2)}.

(f)α1+iα2+jα3，(i,j)∉{(1,1),(1,2)，(2,1)，(2,2)，(2,3),(3,1),(3,2),(3,3)}.

(g)2α1+iα2+jα3，(i,j)∉{(1,1),(1,2)，(2,1)，(2,2)，(2,3),(3,1),(3,2),(3,3),(4,2),(4,3)}.

(h)3α1+iα2+jα3，(i,j)∉{(2,1)，(2,2)，(3,1),(3,2),(3,3),(4,2),(4,3)}.

(a)若λ′-λ=αi，(i=1,2,3)，则aλ,λ′=-v-2.

其中，条件A1：2j-i-k=1；条件B1：2i-j=1.

其中，条件A1：2j-i-k=1；条件D1：2k-j=1.

(d)若λ′-λ=α1+α2+α3，则：

其中，条件A0：2j-i-k=0；条件A1：2j-i-k=1；条件B1：2i-j=1；条件D1：2k-j=1.

(e)若λ′-λ=α1+α3,α1+2α2,2α1+α2,α2+2α3,2α2+α3，则aλ,λ′=v-4.

(f)若λ′-λ=2α1+2α2,2α2+2α3,2α1+α2+2α3,α1+3α2+α3,α1+2α2+3α3，3α1+2α2+α3，则aλ,λ′=-v-6.

(g)若λ′-λ=α1+2α2+α3，则：

其中，条件A2：2j-i-k=2； 条件B0：2i-j=0；条件B1：2i-j=1；条件D0：2k-j=0；条件D1：2k-j=1.

(j)若λ′-λ=2α1+2α2+α3，则：

其中，条件A0：2j-i-k=0；条件A1：2j-i-k=1；条件B2：2i-j=2；条件D0：2k-j=0；条件D1：2k-j=1.

(k)若λ′-λ=α1+2α2+2α3，则：

其中，条件A1：2j-i-k=1；条件B0：2i-j=0； 条件B1：2i-j=1；条件D2：2k-j=2.

(l)若λ′-λ=α1+3α2+2α3，则：

(m)若λ′-λ=2α1+3α2+α3，则：

(n)若λ′-λ=2α1+2α2+2α3，则：

其中，条件A0：2j-i-k=0；条件A1：2j-i-k=1；条件B2：2i-j=2；条件D2：2k-j=2.

(o)λ′-λ=2α1+3α2+2α3，则：

其中，条件A2：2j-i-k=2；条件B1：2i-j=1；条件D1：2k-j=1.

(p)若λ′-λ=2α1+2α2+3α3,3α1+2α2+2α3,α1+3α2+3α3,3α1+3α2+α3，2α1+4α2+2α3，则aλ,λ′=v-8.

其中，条件A1：2j-i-k=1；条件B1：2i-j=1.

其中，条件A1：2j-i-k=1；条件D1：2k-j=1.

(s)若λ′-λ=2α1+4α2+3α3,3α1+4α2+2α3,3α1+3α2+3α3，则aλ,λ′=-v-10.

(t)若λ′-λ=3α1+4α2+3α3，则aλ,λ′=v-12.

证明：(a)对λ′-λ=α1时进行aλ,λ′的求解. 经过计算分析，可以得到其结果只有以下4种情形：

第一，当满足条件2j-i-k=0,2k-j=0时，只有当w=e,s2,s3,s3s2,s2s3,s2s3s2时，有Φ(λ′+ρ-w(λ+ρ))≠0，对于W0中的其他元素，均有Φ(λ′+ρ-w(λ+ρ))=0.

当w=e时，Φ(α1)=-v-2；当w=s2时，Φ(α1+2α2)=v-4；当w=s3时，Φ(α1+α3)=v-4；当w=s3s2时，Φ(α1+2α2+3α3)=-v-6；当w=s2s3时，Φ(α1+3α2+α3)=-v-6；当w=s2s3s2时，Φ(α1+3α2+3α3)=v-8.

同理，当λ′-λ=α2或α3时，可以得到类似的结果.

□

3 结论