车- 隧耦合条件下地铁盾构隧道动力响应分析
陈 昭,杨建伟,刘 传
(北京建筑大学 机电与车辆工程学院 城市轨道交通车辆服役性能保障北京市重点实验室, 北京 100044)
随着城市化进程的加快,城市交通也越发拥堵. 许多城市开始修建轨道交通来缓解路面交通. 轨道交通必然伴随着大量地下隧道的修建. 由于隧道构成和所穿越的围岩条件也不尽相同,运行过程中的问题出现多样化和复杂化的特点. 与此同时,随着轨道交通列车的运行速度的不断提高,列车在隧道中运行所带来的振动也随之加强,车- 线- 隧耦合系统的动力响应问题就有待进一步研究.
近几年,有关地铁隧道结构的动力学研究有所增长. 大量的研究已经从隧道结构的不同部位展开,根据不同工况建立相应的模型,进行模型试验或者数值分析. 有些学者将车辆线路和下部基础耦合起来分析其动力学响应并取得相应进展. 翟婉明等[1]建立了机车轨道动力非线性耦合模型,通过与实测线路实验结果对比,研究机车与轨道的动力作用问题;夏禾等[2]建立了多自由度的车- 桥耦合动力学三维模型,研究车辆在桥上运行过程中的动力响应,并与实验结果对比;梁波等[3]在车- 路系垂直耦合动力相互作用关系等方面的研究取得了较大进展;和振兴等[4]运用有限元的方法,对车辆- 轨道- 隧道进行三维建模,并对简化后的模型分析,讨论了地铁运行的振动规律;金先龙[5]采用多体动力学模型模拟地铁荷载,将车体和转向架看作两个自由度,轮对考虑为一个自由度,对上海某公铁两用隧道进行了动力学分析;宫全美等[6]研究了地铁车辆运行引起的隧道地基土的动力响应;此外各学者[7-11]先后运用不同方法研究隧道结构的动力学响应问题.
有关车辆- 隧道体系的动力相互作用方面的研究虽有涉及但还是较少. 列车在隧道系统中的动力响应是复杂且多方面的,是否建立更加贴近实际的动力学模型直接影响到仿真结果的准确性与可靠性. 所以考虑模型材料的准确性和外部激励与实际情况的一致性很重要. 考虑了列车实际运行的力学性能所建立的运算模型能很好地满足对列车通过隧道时对隧道结构和土体的影响的研究. 为进一步研究列车在隧道结构中运行的长期安全性,保证城市轨道列车运行安全和地铁施工安全,开展车- 线- 隧耦合大系统的研究是合乎时宜的,也是有重要意义的.
1 车辆- 隧道耦合动力学模型建立
1.1 分析思路
不同于以往把车辆系统和隧道系统分别做单独分析,这里将两个子系统通过轮轨接触这个纽带联系在一起,作为一个整体系统进行研究. 通过动力学方程进行解耦分析,动力学方程为:
MA+CV+KX=P
(1)
1.2 车辆模型的假定与建立
不同于以往车- 隧系统只有列车荷载,本系统创造性地运用Simpack软件独立建立地铁车辆真三维模型,并运用模型计算出列车实际运行中移动荷载, 车辆模型的建立分为车身和转向架两部分,每节车有两个转向架,且将车身和转向架均视为刚体,列车为地铁b型车辆,列车拖车模型如图1所示,车体受力如图2所示.
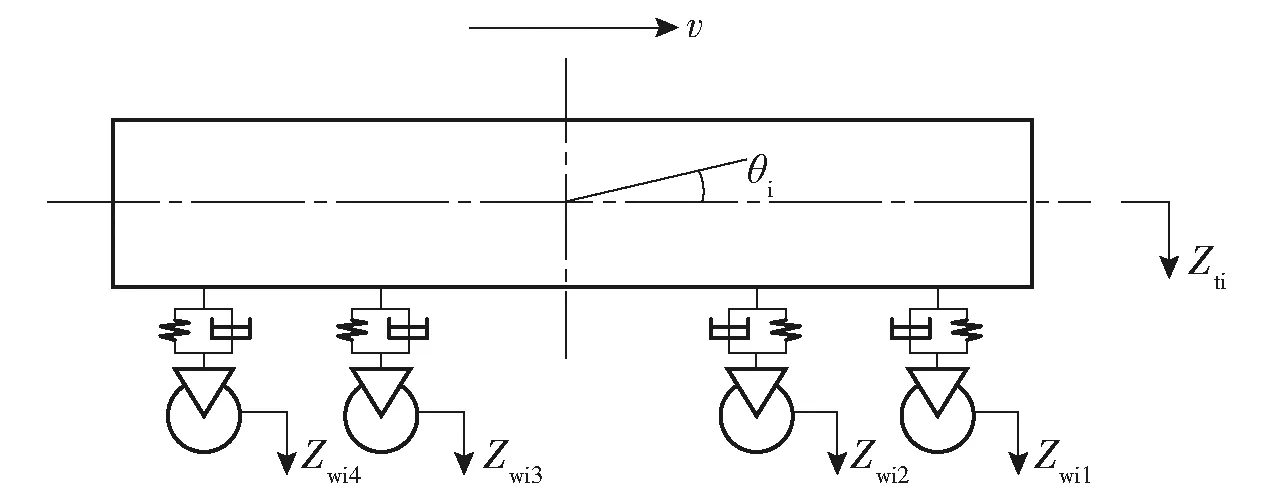
图1 车体计算模型Fig.1 Car body computing model

图2 车体受力分析图Fig.2 Force analysis diagram of car body
经查阅相关文献及相应标准,以及相关研究成果,选取地铁b型车计算其参数见表1[12].
1.3 隧道有限元模型
为了更加真实地模拟隧道的实际情况,考虑土层孔隙水压力作用下系统的动力响应,将车辆模型作为子结构建模,并运用专业岩土类软件MIDAS建立隧道模型. 由于隧道结构一般跨度大,但结构属性基本无变化,因此模型只建立特定区段,而并不是将整个的隧道拿出来分析. 因此应该建立相应的人工边界来切割隧道. 在MIDAS软件隧道建模中将隧道两侧取3~4倍隧道间距,上边界为2倍隧道间距. 隧道结构为盾构隧道,衬砌与轨道板的具体材料参数见表2.

表1 列车参数表
注:其中隧道埋深为12 m,衬砌厚35 cm,轨道结构参数符合规范规定.

表2 轨道系统和隧道结构参数表
因为隧道/轨道结构有限元模型采用的是离散模型,所以要考虑隧道的纵向长度. 经查阅文献,在动力分析中要达到一定的线路长度才能有一个较为准确的精度. 本模型采用的隧道长度为50 m,其中上表面模拟地面为自由边界并施加地面超载,下表面模拟大地为固定边界,侧面采用黏性边界. 隧道/轨道横断面轮廓如图3所示.

图3 隧道有限元模型Fig.3 Tunnel finite element model
根据有限元计算的精度需求,隧道衬砌附近的网格划分较密集,远离隧道的土层采用较为稀疏的网格. 并且整个隧道的土层根据实际情况建立3个土层,分别为粉质黏土层,黏土层,风化岩层. 具体土层属性见表3. 另外钢轨部分用工字梁单元模拟钢轨.

表3 土体力学参数表
1.4 土体本构模型
本次模型的地基土采用弹塑性本构关系来模拟材料的非线性特性. 通常反映岩土、混凝土的屈服和破坏情况的屈服准则主要有摩尔- 库伦(Mohr-Coulomb)屈服准则和德鲁克- 普拉格(Drucker-Prager)屈服准则[13](图4).

图4 Mohr-Coulomb与Drucker-Prager关系示意图Fig.4 Diagram of the relationship between Mohr-Coulomb and Drucker-Prager
由图4可以看出Drucker-Prager准则计算更加准确,本文选用Drucker-Prager准则进行土体本构模型的模拟.
数学表达式为:
(2)
(3)
(4)
式中:I1为应力的第一不变量,I2为应力的第二不变量;α和k可有摩擦角和黏聚力c求得.
2 车辆指标与移动荷载施加
2.1 车辆运行品质指标分析
车辆运行品质这里从3个方面进行考虑:
1)车体的振动加速度可以由Simpack分析直接得到;
2)车辆动轮重Pijω:
由轮对沉浮运动可求得轮对对钢轨的作用力:
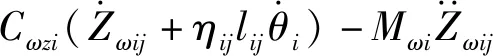
(5)
式中:Pijs为车辆的静轮重;Kωzi为轮对弹簧刚度;Mωi为第i节车体的轮对质量;Zωij为第i节车体的第j轮对的竖向位移;Cωzi为轮对阻尼系数.
3)轴重减载率:
(6)
式中:Pijw为列车运行时的动轮重;Pijs为平均静轮重.
经计算可以得到车辆的最大加速度处于合理水平,最大动轮重与轮重减载率分别低于250 kN和0.6的舒适性判断标准. 因此车辆运行品质可以保证后面隧道动力分析的准确性与可靠性.
2.2 移动荷载施加
前面讲述了车辆和隧道的计算参数,列车模型为6节编组的地铁b型车,最高时速为120 km/h. 本次仿真采用80 km/h,为增加仿真准确性,考虑孔隙水压力存在的情况下对轨道板施加移动荷载并进行有限元计算. 计算时间为6 s.
移动荷载为车辆模型在Simpack中计算得到,由于轮轨接触的受力可以转化为扣件与轨道板的力,这里将移动荷载施加在轨道板上扣件位置[14]. 图5、图6为列车动力荷载加载位置和列车动力荷载时程曲线.

图5 移动荷载布置图Fig.5 Mobile Load Layout

图6 移动荷载时程曲线Fig.6 Time-history curve of moving load
3 隧道计算结果与分析
为了反映隧道衬砌上不同位置的动力响应,在y=15 m处隧道断面上,选区了4个典型位置,其中Cir-1位于受载钢轨正下方,Cir-2和Cir-4为轨道板与衬砌接触的地方,另外再取一个距荷载施加位置较远的Cir-3点作为对比,这里取位于隧道顶部与中心线程30°角的位置. 4个位置如图7所示.

图7 衬砌环不同位置取点示意图Fig.7 Diagram of different locations of lining ring
3.1 衬砌单元同一断面不同位置各指标时程曲线分析
在移动荷载作用下,衬砌上3个位置应力时程曲线如图8至图11所示,每节列车运行过程中应力变化对应不同轮对主应力大小不同,其中最大主应力位置Cir-1达到0.7 MPa,3个位置均为拉应力;对于最大剪切力位置Cir-2大于其他2个位置,最高为0.54 MPa. 主应力和最大剪切力均小于该处土体的容许应力,土体不会出现破坏.

图8 最大主应力时程曲线Fig.8 Maximum principal stress time history curve

图9 最大剪应力时程曲线Fig.9 Time history curve of maximum shear stress

图10 加速度时程曲线Fig.10 Acceleration time history curve
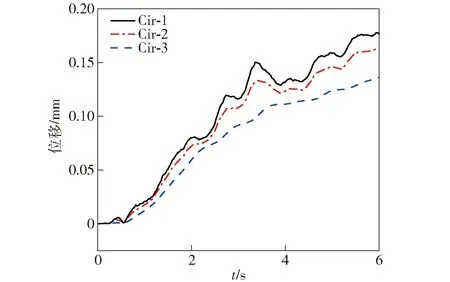
图11 位移时程曲线Fig.11 Displacement time history curve
从应力时程曲线可以看出,处于轮轨正下方的Cir-1位置处的应力动力响应最强烈,在隧道左上方的Cir-3位置动力响应最弱,符合衬砌各位置动应力分布规律.
移动荷载作用下,隧道衬砌不同位置的加速度响应与位移时程曲线如图12和图13所示,可以看出位置Cir-1处加速度的动力响应最为明显,且和列车动力荷载作用频率相吻合,加速度动力响应最大处出现在轮轨正下方的衬砌位置;由图可以看出位置Cir-1处的位移最大,最大达到0.18 mm.
根据前述分析可知隧道衬砌总体动应力水平较低,但出现明显的加卸载过程. 动应力在3.5 s左右时刻达到一个峰值,根据列车运行速度80 km/h可以推断出,此时的y=15 m断面恰好处在整列列车中部位置,此时动应力响应最为强烈. 衬砌管片的加速度和动应力响应均有一定的循环特征,在列车长期的移动荷载作用下,这种特征可能会带来衬砌结构的变形以及疲劳损伤. 因此在地铁运营期应及时做好防护和定期检查.
3.2 衬砌弯矩和轴力的动力效应和速率效应

图12 不同速度下弯矩与轴力分布图Fig.12 Distribution Diagram of Bending Moment and Axis Force at Different Velocities
对于隧道衬砌环向轴力和弯矩,分别进行没有列车荷载,和附加列车荷载下的计算. 这里取环向轴力和弯矩最大位置处如图12所示,图12(a)在附加移动荷载的情况下,隧道弯矩相比于不附加移动荷载时有所增加,增幅在12%左右;在附加不同速度移动荷载的情况下,弯矩大小会有速率效应的影响,不过影响幅度较小. 图12(b)所示,隧道衬砌的轴力受移动荷载的影响与弯矩相似,在附加移动荷载的情况下增幅为11%左右,同样速率效应不明显.
不同时刻,隧道的合弯矩和合轴力是不同的,这是由于列车的动力作用对隧道的动力响应造成的. 图13是列车荷载激励对某一截面隧道合轴力和合弯矩的影响的时程曲线. 这里考虑y=40 m截面处,列车速度为80 km/h,所以第一个荷载到达截面出的时间为40÷22.2=1.8 s.

图14 t=3 s时刻隧道轴力图Fig.14 t=3 s time tunnel axial force diagram

图13 动力作用下的合轴力与合弯矩时程变化Fig.13 Axis resultant force and time-history change of resultant moment under dynamic action
图13可以看出随着第一个荷载经过y=40 m断面,轴力合力不断增大,最大值为257.2 kN,合弯矩的趋势和轴力合力大体相同,最大值为312.3 kN.
3.3 同一时刻不同断面Cir-1位置处正压力与轴向力
图14为t=3 s时刻隧道两个方向的轴力图云图.
在3 s时刻,y=10 m,y=20 m,y=30 m,y=40 m 4个断面,在移动荷载作用下Cir-1位置的竖直和沿隧道走行方向的动应力如图15所示,单位为kPa.

图15 3 s时刻不同断面处的Cir-1位置的动应力水平Fig.15 3 s Dynamic Stress Level at Cir-1 Location at Different Section
由图15可以看出,同一时刻不同断面均处于移动荷载作用下,其动应力响应的程度不同且方向不同,其中同一位置拉应力和压应力交替变换,受拉应力和压应力均处于衬砌结构最大容许应力范围内. 由此可见,在同一时刻,不同位置断面受力状态是不相同的.
4 结论
地铁列车在盾构隧道运行中,引起的动力响应是多方面的. 建立相对完善的并能够较为准确地模拟实际工况的车辆- 线路- 隧道耦合分析模型,施加接近实际情况的动力荷载,是得到相对准确结果的关键所在.
因此,本文运用精确建模技术,建立车辆- 线路- 隧道耦合模型,通过Simpack计算出车辆移动荷载加载到扣件处以模拟实际工况,研究盾构隧道衬砌结构在移动荷载作用下的动力响应,得到结论如下:
1)隧道衬砌环向经过多次加载卸载过程,不同位置的动力响应状态各不相同,但总体动应力水平较低,对隧道结构影响较小.
2)隧道衬砌底部受动力响应程度大于隧道顶部,随着位置不同,动应力响应程度不同. 衬砌管片的加速度和动应力响应均有一定的循环特征,在列车长期的移动荷载作用下,这种特征可能会带来衬砌结构的变形以及疲劳损伤. 因此在地铁运营期应及时做好防护和定期检查.
3)隧道衬砌环向弯矩与轴力,在施加移动荷载时有显著增大,速率效应虽不明显,但也应该引起足够重视. 隧道轴力合力与合弯矩变化随时间变化趋势大体相同.
4)同一时刻不同断面的动力响应不同,方向大小都有变化,且动应力绝对值均较小,不会引起隧道结构破坏. 运营阶段需重视特殊断面隧道损伤,及时进行维修加固.

