基于Lagrange与灰色关联分析的工程特性耦合排序方法
路可欣,秦建军
(北京建筑大学 机电与车辆工程学院 城市轨道交通车辆服役性能保障北京市重点实验室, 北京 100044)
在激烈的市场竞争中,企业从“以产值为中心”逐渐过渡到“以用户需求为中心”的观念上,对用户需求做出快速响应,成为赢得市场的关键所在[1-2]. 相关的设计方法众多,例如质量功能展开(Quality Function Deployment,QFD)、公理化设计(Axiomatic Design,AD)等,确定用户需求与产品的关系,进一步将用户需求转化为工程特性,工程特性的精准获取以及重要度的科学排序,有利于研发人员掌握产品设计初期到投向市场过程中的完整信息,生产符合市场需求的产品,以增强核心竞争力[3-5].

图1 基于Lagrange与灰色关联分析的工程特性耦合排序方法流程图Fig.1 Flow chart of coupling method of engineering characteristics based on Lagrange and gray relational analysis
为此国内外学者对工程特性重要度排序的问题进行了大量研究[6-7]. 耿秀丽等[8]采用三角模糊数的方法,解决了工程特性评价的模糊性. 张根保等[9]将模糊层次分析法与信息熵结合,对产品的工程特性重要度进行排序,进一步消解了传统方法中存在的主观性与不确定性问题. 李延来等[10]综合考虑初始重要度、竞争性评价以及企业改进目标对最终工程特性重要度的影响,通过平衡计分卡(BSC)确定重要度. 为进一步提高排序精度,王萌等[11]提出等价支持子集的工程特性重要度计算方法. 为克服工程特性与产品设计间存在的较大差异,CHAN等[12]在工程特性的分析中引入可行性控制环的概念. 李延来等[13]引入实现工程特性改进比率重要性的概念,根据工程特性的目标值确定产品改进比率,并进行了定性与定量分析,进而提出基于用户满意度的工程特性重要度与实现工程特性重要度改进比率的综合排序方法.
由此可以看出,在产品工程特性重要度排序的问题上,大多数学者从产品设计初期的关联性、消解主观性或提高排序精度等单方面对该问题进行研究[14-15],为此本文提出了基于Lagrange与灰色关联分析的工程特性耦合排序方法,从消解评价的主观性与专家偏好差异的角度考虑,为工程特性重要度排序提供了新思路.
1 集成方法设计思路
面对复杂产品设计中用户需求及其对应的工程特性数量繁多的问题,必须对工程特性重要度加以确定,以避免非关键工程特性信息的干扰. 通过大量文献调研,相关研究结果众多,但传统QFD质量屋中的工程特性重要度排序仍存在如下不足:
1)对工程特性信息要求高,从而降低了QFD应用的适应性;
2)传统QFD缺乏数据处理过程,无法减少或消除信息的不完整性,即灰性;
3)传统QFD质量屋中,用户需求与工程特性间的关联关系采用自然数数值序列进行简单确定,存在专家偏好且误差较大的问题.
针对传统QFD质量屋工程特性的不足,本文分别从消解主观性与专家偏好两方面进行考虑,作出了如下创新:
1)采用灰色关联分析理论进行工程特性分析,对其重要度逐一进行明确,以消除和减少信息的不确定性;
2)利用拉格朗日模型将信息量化表达,以求得最优解,从而消解专家偏好. 具体集成方法设计思路流程如图1所示.
2 灰色关联分析
灰色关联分析(Gray Relation Analysis,GRA)是对离散空间中序列曲线紧密度进行判断的工具,与其他判断工具比较,具体如表1所示. 与其他判断工具相比,灰色关联分析具有计算量小且数据要求较低等特点,曲线越离散,对应的序列关联度越小,反之,曲线越密集,对应的序列关联度越大.

表1 4种典型判断工具对比
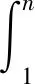

图2 灰色关联分析Fig.2 Gray relation analysis

由于打分数据中出现了具体数值,同时也出现了例如相对重要、一般重要等字样,存在信息的不确定性,该系统满足灰色关联分析理论,QFD团队专家给出的语言真值,无法定量化比较,因此需将定性指标量化,其具体步骤如下:
Step 1.确定基准点以及参考序列

Step 2.将比较序列进行标准化
因工程特性重要度与用户需求呈正比例增长关系,故采用最大值标准化法对原始数据进行标准化处理:
(1)
(2)
Step 4.确定灰色关联系数:
(3)

同时可将工程特性进行划分,可分为效益性、成本型与稳定型3类. 其中效益型指产品工程特性越大越好的特性,成本型指产品工程特性越小越好的特性,稳定型指工程特性值趋于某个固定值μj,如图3所示,可用Op(p=1,2,3)分别表示效益型、成本型与稳定型3类工程特性,对其进行工程规范化处理:
(4)
(5)
(6)

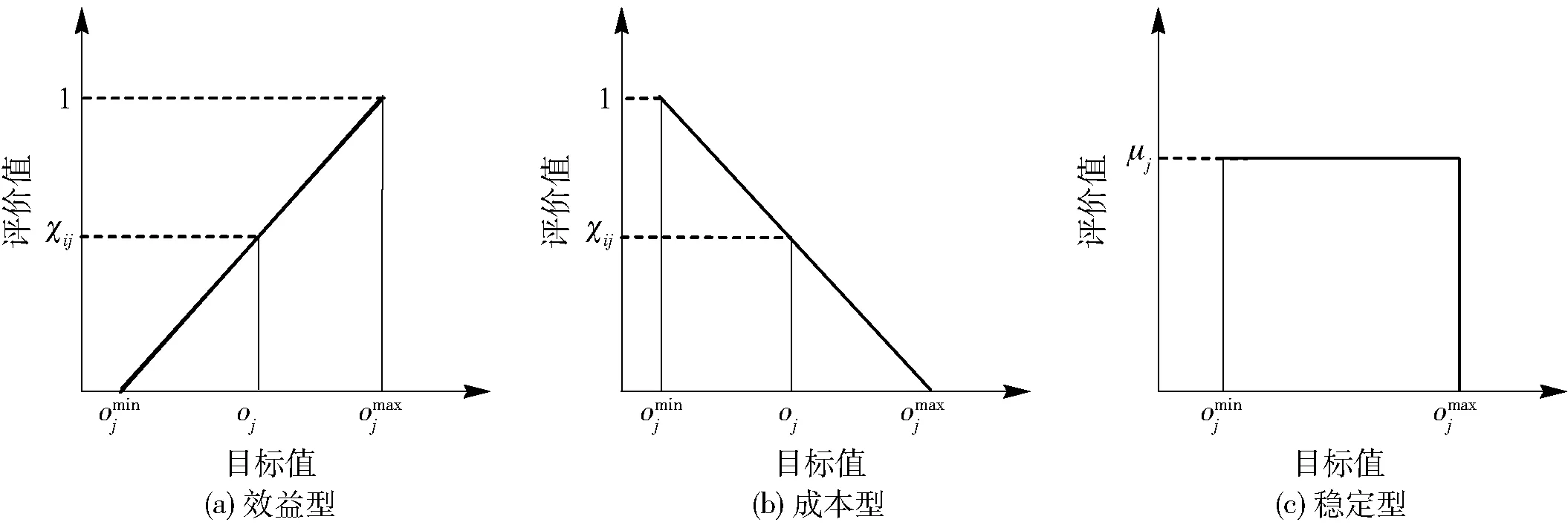
图3 3种工程特型类型Fig.3 Three types of engineering types
3 构建拉格朗日模型


表2 i元素与j元素比较含义


(7)


(8)

(9)
上述偏差值越小越好,可建立优化模型:
s.t.

(10)
构建拉格朗日模型对优化模型进行求解:
(11)


(12)
即:

(13)
若令GM=(1,1,…,1),QM=(q1,q2,…,qm),V=(vij)M×M,其中:
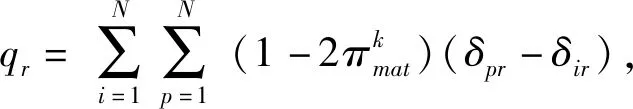
(14)
且:

(15)
则式(13)可转化为:
(16)
式中:V为正定矩阵.
(17)
通过式(16)与式(17),求得最优解:
(18)
4 案例分析
液压四足机器人因其在非结构地形下出色的环境适应性以及高负载性等特点,在野外可完成运送弹药、运输伤员等复杂任务,从而得到了国内外学者的普遍关注. 在众多需求的情况下,对机器人工程特性重要度进行合理排序,可大大提高整机性能. 为此本文分别从消解评价主观性与专家偏好差异两方面综合考虑,对液压四足机器人工程特性重要度排序进行研究.
4.1 确定用户需求与工程特性

4.2 基于灰色关联分析消解评价主观性
考虑到液压四足机器人质量屋模型中的用户需求与产品工程特性间存在“少数据”以及“贫信息”的特点,相对样本数量较少,故将灰色关联分析引入到质量屋中,以消解评价的主观性. QFD团队相关专家根据已有经验以及前期大量文献调研,分别对美国波士顿动力学公司的Big Dog、Spot Mini机器人,意大利技术研究院的HyQ机器人、西班牙教育学院的SILO4机器人、山东大学的SCalf机器人等等较为有代表性的液压四足机器人进行多方面研究,从设计、制造、质量管理等方面考虑,从而对用户需求与工程特性之间的相对重要度进行打分. 根据每一需求与工程特性的关联程度,在0~9数值标度法进行取值,并将多位专家打分结果进行均值化,以提高评价的客观性,综合打分结果如表3所示.

表3 液压四足机器人用户需求与工程特性相关


表4 液压四足机器人用户需求与工程特性灰色差序列
同理可计算其他值,结果如表5所示.

表5 液压四足机器人灰色关联系数矩阵


表6 消解评价主观性的工程特性相关重要度
4.3 基于Lagrange消解专家偏好差异
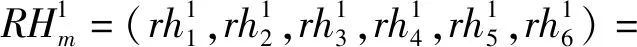
同理计算其他专家的液压四足机器人各工程特性的竞争优先度,结果见表7所示.
表712名专家对液压四足机器人工程特性竞争优先度评价
Tab.7 Evaluation of competition priority of engineering characteristics of hydraulic four-legged robot by 12 experts

ωoi1ωoi2ωoi3ωoi4ωoi5ωoi6τoin10.1330.1970.1360.1790.1390.216τoin20.1520.2060.0820.1970.1580.205τoin30.1570.2310.0150.1870.1970.213τoin40.1670.2050.0750.1980.1540.201τoin50.1670.2110.0860.1570.2040.175τoin60.1870.2130.0290.1680.2140.189τoin70.1510.2220.0400.2050.1870.195τoin80.1570.1860.0960.1970.1990.165τoin90.1550.1880.0210.2160.2050.215τoin100.1680.2020.0510.2310.1470.201τoin110.1540.2130.1220.1670.1680.176τoin120.1570.2030.1010.1740.1790.186


表8 消解专家偏好差异的工程特性相关重要度
4.4 液压四足机器人工程特性重要度最终排序

5 结论
QFD应用于产品设计的关键一步就是对工程特性的精准排序.
1)基于Lagrange与灰色关联分析的工程特性耦合排序方法,可利用灰色理论模型消解评价的主观性,建立工程特性竞争优先度优化模型,通过拉格朗日函数对其求解,以此消解专家偏好的差异.
2)将其应用于液压四足机器人设计的工程特性重要度排序中,使排序精度得以提升.
3)与已有排序方法相比,该方法为消解评价主观性与专家偏好差异的问题提供了新思路,使工程特性排序更加科学可靠.
4)在实际的产品设计中,实现工程特性到用户需求的快速响应,使企业以一种高效经济的方式对产品进行设计,提高用户满意度,从而提升企业整体的核心竞争力.

