基于LabVIEW的振动信号分析系统设计

李思琦，蒋志坚

(北京建筑大学 电气与信息工程学院， 北京 100044)

振动是一种在自然界中普遍存在的现象，它往往会对机器设备造成负面影响[1]. 在机器设备工作的过程中，持续、剧烈地振动往往会导致机器设备部件发生损坏，进而影响整个设备的性能和寿命. 随着工业制造水平不断提高，机械设备结构日益精密复杂，对机器设备运行状态的监测变得越来越重要. 对机械设备进行运行状态监测不仅能及时了解机器的运行状态，还能够尽早发现问题，从而避免故障进一步扩大而导致的严重后果.

振动信号包含的信息极为丰富，对其进行监测无法反映出所需要的有价值信息. 因此需要对其进行进一步分析[2].

目前对机械设备在运行过程中产生的振动信号进行研究的主要方法是结合时域、频域、时频域相关波形对振动信号进行分析[3-5]. 除此之外，使用智能算法在对振动信号进行处理的过程中还能够对机械设备进行故障诊断[6-8]. 这些方法大多通过MATLAB、LabVIEW等平台编程实现，或通过Visual Studio软件编程来实现. MATLAB平台编程过程较为复杂且可视化较差，微软公司的Visual Studio软件虽然可以实现可视化界面的开发，但其要求开发人员有较高的编程水平，制约了其在实际中的应用[9].

LabVIEW软件平台使用其特有的图形化编程语言完成整个开发设计的过程. 信号分析系统开发设计的过程简单快捷，用虚拟仪器技术及VI模块对振动信号进行处理能高效、直观地显示出振动信号中所包含的丰富信息. LabVIEW软件还提供了与MATLAB软件的接口，使用LabVIEW时可以借助MATLAB软件强大的计算能力，使分析结果更准确、可靠[10]. 本文选择使用LabVIEW作为振动信号分析系统的开发软件.

1 信号分析系统总体设计

1.1 系统功能设计

本文研究内容为振动信号分析系统，对振动信号的采集部分不做介绍. 为了实现对信号的分析任务，信号分析系统应当至少具备如下功能：

1)信号读取. 本系统不涉及信号采集部分，数据来源一般为txt、Excel等格式的电子文本，因此系统应当具备从数据文件中进行数据读取的功能.

2)信号预处理. 数据文本中的原始信号是由数据采集系统进行数据采集得到的信号. 由于采集硬件老化、环境因素影响、试验操作失误等多种原因，在原始信号中会不可避免地带有大量的噪声信号. 这些噪声信号对后续进行信号分析得到的结果准确性有着极大的影响. 为了使分析效果变得更加准确，因此需要对原始信号进行预处理，从而减少噪声信号的影响.

3)数据分析. 在原始信号经过预处理后，对信号在时域以及频域内展开分析，计算相应的特征指标如峰值、峭度值、有效值、功率谱等.

4)数据存储. 为了在后期方便查看分析结果或展开进一步研究，需将预处理后的数据、计算得到的特征指标等保存为电子文本文件.

5)数据显示. 为增加系统的可视性，在系统分析过程中应具备结果显示功能.

1.2 系统流程设计

确定系统功能后，再根据模块化程序设计思想，完成系统的流程设计. 本文设计的信号分析系统流程如图1所示.

图1 系统流程图Fig.1 System flow chart

2 信号分析系统开发

根据信号分析系统总体设计，本文利用LabVIEW软件对各个功能部分进行开发.

2.1 数据读取部分开发

LabVIEW提供的文件I/O模块能对多种类型的文件进行读写操作，其中包含文本文件(.txt)、电子表格文件(.xls)、二进制文件(.bin)等，该模块的各端口意义如图2所示.

图2 信号读取模块端口意义Fig.2 Meaning of signal reading module port

将需要读取的数据文件地址引入到“文件名”接口即可实现对数据文件的读取，由信号输出端输出数据文件中的数据.

2.2 数据预处理部分开发

在数据读取完成以后，需要对其进行预处理，从而减小在信号采集过程中由于操作不当或者硬件问题带来的干扰. 常用的预处理方法有：去趋势项、滤波降噪、加窗处理、小波降噪等.

2.2.1 去趋势项

(1)

(2)

其中(i=0,1,…,m). 解式(2)所示方程组，即可得到m+1个待定系数a. 当m=0时，求得的待定系数为：

(3)

此式算得的结果为原始振动信号的算术平均值，消除趋势项的结果为：

yk=xk-a0

(4)

即用原始信号减去算术平均值即可实现消除原始信号中趋势项的目的[11].

2.2.2 滤波降噪

滤波降噪是降低干扰对原始信号影响的有效方式. 传统的方法是根据所需成分所在的频率区间选择低通、高通、带通等不同拓扑结构的滤波器对信号进行处理，由原始信息得到所需的频率成分. LabVIEW软件提供的滤波器VI可以简单快捷地实现对滤波器拓扑结构的选择以及频率区间的设定，其端口定义如图3所示.

图3 滤波器模块端口定义Fig.3 The meaning of filter module port

根据图3所示，经过读取及预处理后的信号由信号端输入到滤波器VI中，滤波器VI默认的拓扑结构为低通滤波器，在“低截止频率”处设置截止频率，在“滤波后的信号”端接收滤波后的信号.

2.2.3 加窗处理

图5 小波降噪程序框图Fig.5 Block diagram of wavelet denoising program

对信号进行加窗处理主要为了使信号的频域分析结果更准确. 进行频域分析时，时域信号需要通过傅立叶变换转化为频域信号，傅立叶变换是针对无限长时间的，而在实际试验过程中不可能进行无限长时间采集，这就会导致出现“泄漏”现象. 对信号进行加窗处理可以有效减少这种现象带来的影响. LabVIEW软件集成了多种窗函数，在进行信号分析的过程中可以自由选择，该过程的程序框图如图4所示.

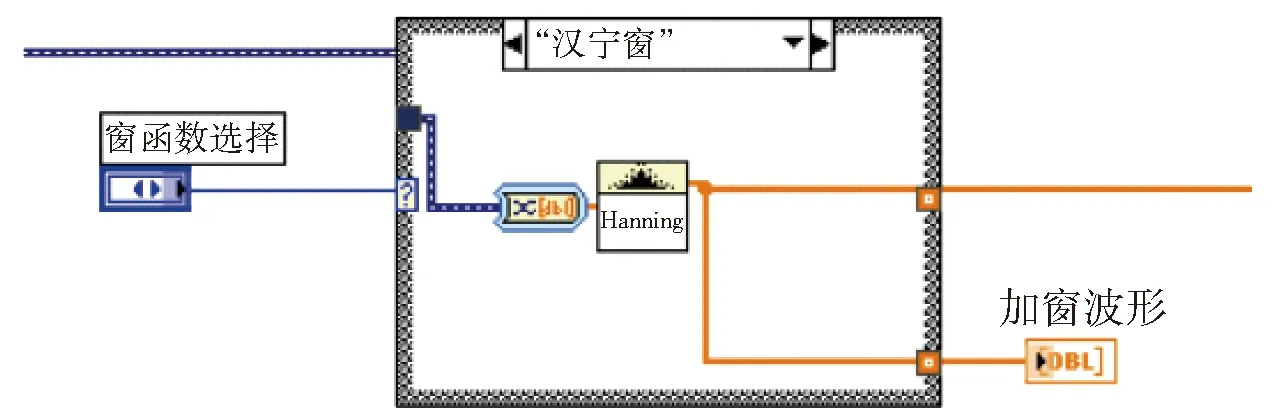
图4 窗函数处理Fig.4 Window functions processing

2.2.4 小波降噪

除了使用传统的滤波器对信号进行滤波降噪之外，应用小波变换的方法也可对信号进行降噪. 小波变换可以有效地从待处理的信号中分离出噪声或者其他无意义的信息. 小波降噪过程如下：

1)分解过程：在多种小波基中选择合适的小波基对信号进行小波分解.

2)作用阈值过程：对分解后的各层系数选择阈值，并对细节系数进行处理.

3)重建过程：处理后的各分量通过小波重构，组成降噪后的信号[12].

在使用小波分析对数据进行处理的过程中，需要借助MATLAB软件计算能力. LabVIEW提供了两个软件之间进行连接的“桥梁”——LabVIEW中的“Matlab script”模块. 将程序的输入输出变量按照需求设置好，利用这个节点在LabVIEW环境下运行MATLAB特有的M文件，结果可直接显示. 通过LabVIEW调用Matlab实现小波降噪的程序框图如图5所示.

2.3 数据分析部分

对原始信号进行一系列的预处理之后，为了更好地体现信号中包含的丰富信息，还需对其进行时域和频域信号特征分析.

在时域分析部分，主要对信号的峰值、均方值、峭度进行统计. 其中峰值、均方根值计算公式为：

峰值：

xp-p=xmax-xmin

(5)

均方根值：

(6)

峰值与均方根值主要体现的是一组数据的整体振动情况以及最大振动幅度. 峭度是一个无量纲的参数，它对于振动冲击信号极为敏感，因此该数值常被用来检验轴承故障. 在轴承还未出现故障损伤的时候，K值接近于3；当轴承出现故障时，峭度值会与正常值偏离. 当峭度的数值大于8时，可以认为轴承出现了较为严重的故障[13].

由于时域统计量在机械结构出现故障初期并不会有太明显的变化，因此仅从时域分析的结果对机械设备的状态进行分析是不够全面的. 机械结构出现细微的故障会在信号的频域中增添新的频率成分，因此为了对信号进行更全面的分析，还需要对信号进行频域分析. 傅立叶变换为信号从时域转换为频域提供了通道. 对频域信号进行分析的方法主要有绘制信号的幅值谱以及功率谱. 在幅值谱中体现了信号所包含的频率成分以及每个频率的幅值大小. 在功率谱中则体现了信号所包含的能量与信号频率成分[14]，功率谱能够更好地体现信号中所包含的频率成分.

根据上述内容，在LabVIEW软件中完成程序的编写，开发设计完成后的系统如图6所示.

图6 系统程序框图Fig.6 System program block diagram

根据图6所示程序框图，系统首先完成数据的读取，随后可以点击“去趋势项”按钮完成相应的预处理操作，在一定程度上减少噪声信号的干扰. 随后通过小波降噪的方法与滤波降噪再一次对信号进行处理，最后对信号在时域以及频域中对其展开分析，并显示分析结果. 最终分析结果可以根据需要选择是否保存.

3 信号分析系统功能验证

为验证设计的信号分析系统的正确性，本文下载了美国凯斯西储大学的轴承实验数据并使用信号分析系统对其进行了处理.

这些数据是在进行某电机轴承状态评估实验中测得的. 试验过程中，使用电火花加工技术在轴承上分别人工制造了直径为0.007英寸、0.014英寸、0.021英寸的单点故障，试验所使用的轴承为SKF- 6205- 2RS深沟球轴承，采样频率为12 000 Hz. 试验使用的轴承参数：节圆直径D为39.04毫米，滚珠直径d为7.94毫米，接触角β为0°，滚珠数量n为9[15]. 内圈故障特征频率计算公式为：

(5)

外圈故障特征频率为：

(6)

滚体故障频率为：

(7)

由于滚体会同时撞击轴承的内圈与外圈，因此在计算滚体故障频率时需要结果加倍. 按照式(5)～式(7)，将所用轴承参数带入，可以计算出此轴承的内圈故障频率、外圈故障频率以及滚体故障频率分别为162.185 Hz、107.364 Hz以及141.091 Hz.

根据上述计算结果，为了能够更好地观测到故障频率，在滤波的过程中过滤掉高频信号，仅保留0～500 Hz的信号成分. 在确定了滤波器截止频率的设定值后，使用本文设计的信号分析系统对这些信号进行处理，部分结果如图7所示.

图7 信号滤波结果Fig.7 Signal filtering result

根据图7所示内容，不论是正常轴承振动信号还是内圈损伤信号，在经过滤波降噪处理后信号幅值都有所减少，这是因为超过截止频率部分的数据被“过滤”掉了. 对此时的信号使用小波降噪方法对其进一步降噪. “小波降噪”操作界面如图8所示. 首先选择适当的小波基，并且设置小波阶数与分解层数，随后单击“执行数据分析”降噪操作.

信号经过一系列的降噪处理后，对其进行时域以及频域分析，分别统计相应的指标，利用这些指标对轴承的状态进行判定，将判定结果与实际结论进行对比，验证分析结果的准确性. 经时域以及频域分析后，部分结果如表1所示.

图8 小波降噪结果Fig.8 Wavelet denoising result

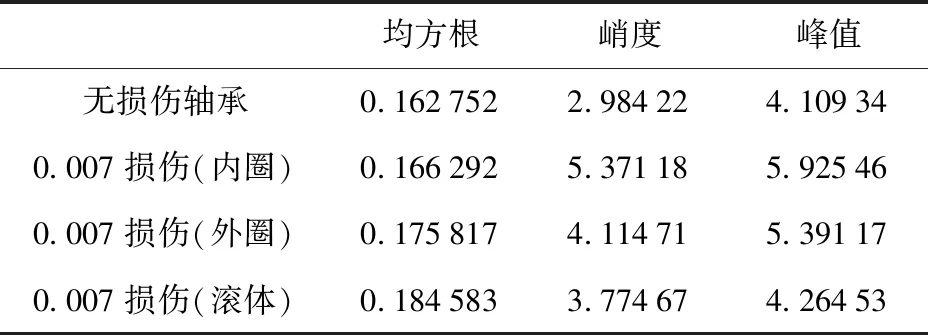
表1 信号时域分析结果

根据系统对各组数据进行分析可知，有损伤的故障轴承数据与无损伤轴承数据在均方根数值计算结果上相差不大，这也在一定程度上证明了通过计算某些时域指标作为轴承状态判定依据的方法是不严谨的. 通过表1可知，峭度值的统计结果有着明显的差异，故障轴承的峭度值与正常值3有着一定的偏离. 因此在时域分析部分能够识别出可能有故障的轴承. 为了更好地判断轴承是否发生故障以及发生故障的位置，需要对信号进行频域分析，根据信号在频域的分析结果再次进行判断.

本文涉及的3种故障的故障频率分别为162.185 Hz、107.364 Hz和141.091 Hz. 为了更好地展示这部分的信号，在进行滤波的过程中人为设置了滤波器的截止频率为500 Hz，使用信号分析系统对正常轴承信号、内圈损伤信号、外圈损伤信号以及滚体损伤信号进行频域分析，得到的功率谱图如下图9所示.

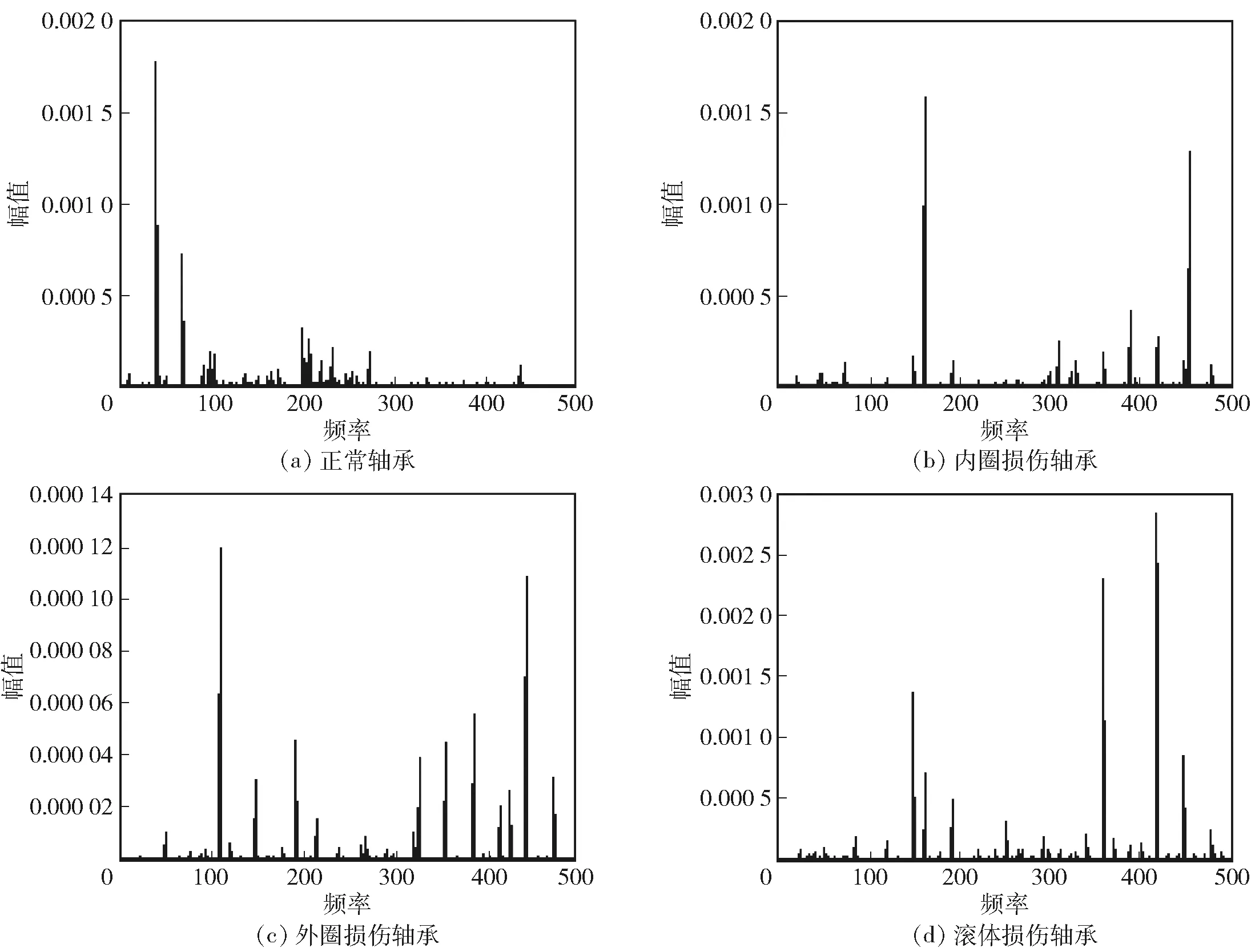
图9 频域分析结果Fig.9 Frequency domain analysis results

根据图9所示的频域分析结果，能从图片上分别看到各轴承的功率谱图. 正常轴承的频率成分主要集中在低频部分，3种故障类型的故障频率以及其倍频能够在各自的功率谱图中较为明显地看到，且数值与理论分析计算结果相近，与轴承的故障原理一致. 由此可以认为，本文所设计的信号分析系统能够对信号进行处理与分析，且处理分析结果较为准确.

4 结论

本文使用LabVIEW软件开发设计了一套应用于振动信号的信号分析系统，并使用实际试验信号对系统功能进行了正确性验证，试验表明，本系统能够对振动信号进行较为准确的分析，系统分析的结果可以作为诊断被测物体状态的依据. 与目前存在的振动信号分析系统相比，本文所开发设计的系统使用G语言对系统进行设计，大大减少了开发设计所需要的时间，且系统操作简单、结果显示直观、可拓展性好. 利用软件自有函数建立了与Matlab之间的连接，加强了整个系统的性能，使其在进行信号分析以及故障诊断的过程中有着较好的应用前景.