机器人变阻尼柔顺驱动关节设计

冯志友，许文斌，智 德，康荣杰，陈丽莎

（1.天津工业大学 机械工程学院，天津 300387；2.天津大学 机构理论与装备设计教育部重点实验室，天津 300354）

在传统工业领域，机器人取得了重大发展，可以实现很高的位置精度和精确的轨迹跟踪，提高了生产力。随着时代发展，机器人的应用范围逐渐变大，不仅应用于工业领域，而且应用于生活、娱乐等各个方面，逐渐开始与人直接接触，必须适应更加复杂的环境。而传统机器人刚度大、速度快，一旦与人发生碰撞，必然会对人造成严重的伤害，机器人与人机环境交互的安全性问题逐渐进入人们的视野[1-5]。

串联弹性驱动器（series elastic actuator，SEA）在驱动电机与负载之间加入弹性元件，利用自身机构的柔性变形来完成力和运动的传递[6]，所以整个机构的刚度显著降低[7]，通过实时检测弹性环节的变形量，将力控制问题转化为位置控制问题[8]，可以较好地减少机器人碰撞时产生的冲击影响。但是SEA 的刚度是固定的，无法适应于不同的工况，并且加入的弹性元件将不可避免地带来振动。

比萨大学 Tonietti 等[9]和 Grioli 等[10]设计了一种可变刚度驱动器（variable stiffness actuator，VSA），采用拮抗原理，通过用滑轮按压或松开来改变输出刚度。Lefeber[11]指出此类变刚度驱动器可以将关节的动能和势能进行转换。考虑到安全性和响应性，近年来其他学者又提出了各种结构优化的变刚度执行器[12-14]，且一些学者把此类驱动器应用于机器人[15-17]。与SEA 相比，VSA 可以主动改变刚度，因此具有更好的适应性。然而，弹性元件引起的振动问题仍然存在。变物理阻尼驱动器（variable physical damping actuator，VPDA）是由意大利理工学院Laffranchi 等[18-20]提出的。VPDA 是在传统SEA 的基础上设置一对压电陶瓷驱动的摩擦副，可根据当前速度调节压电陶瓷长度，以改变摩擦副的正压力和库伦摩擦力，从而模拟出粘滞摩擦的效果，使关节产生期望的阻尼。该设计有助于减少系统振动，实现能量的存储和释放，但并非真正的粘滞阻尼控制。由于压电陶瓷所产生的位移非常小，难以精确调控所产生的库伦摩擦力，因此阻尼的控制精度并不高。此外，当阻尼增加时，需要使陶瓷持续工作以提供摩擦力，额外能量损耗巨大。

针对上述问题，本文提出了一种新的解决方案。在SEA 的基础上，采用流体节流原理产生期望的粘滞阻尼，调控系统的动态性能。封闭节流孔后，可以完全锁定机构，使其变成完全刚性，且无额外的能量损耗。相比VPDA 用库伦摩擦力模拟粘滞阻尼力，本设计直接由流体产生粘滞阻尼力，有很高的阻尼调节范围及精度。

1 变阻尼柔顺关节的设计

1.1 设计思路

传统的串联弹性驱动关节采用电机—输入端—弹性单元—输出端的结构模式，该模式结构紧凑，可以有效地增加关节柔性。本文以该结构模式为基础，在输入输出端之间增加变阻尼模块，使变阻尼模块与弹性单元耦合；主电机带动输入端转动，输出端连接负载；变阻尼模块的阻尼系数由变阻尼电机调整。其关节原理如图1 所示。

图1 变阻尼关节原理Fig.1 Principle schematic of variable damping joint

因为本柔性驱动关节多用于腿式或手臂式机器人，所以关节尺寸较小，要求关节直径在170 mm 以内，关节长在300 mm 以内。本设计需要以阻尼来减小系统的振动，所以阻尼系数需要较大的变化范围，期望的阻尼变化范围为0 到无穷大，即输入端与输出端完全锁死，无相对速度。由于柔顺关节经常承受振动和应力作用，需要具有很高的疲劳极限和弹性极限。所以选择一对弹簧作为弹性单元，弹簧的材料选择弹簧钢。变阻尼模块要改变粘滞阻尼力，若采用机械结构的摩擦力来模拟粘滞阻尼力，控制起来非常复杂。因此，本文利用流体原理直接产生粘滞阻尼力。采用旋转液压缸来产生阻尼力，在活塞上开节流孔，通过改变节流孔面积来改变阻尼系数。曲柄滑块机构磨损轻，寿命长，传递动力大，所以本文选取曲柄滑块机构做为传动机构，来推动挡块改变节流孔面积。

1.2 变阻尼机构几何参数设计

节流孔选用矩形孔，因为矩形孔的面积与挡块的位移呈线性关系，便于控制。节流孔越长，调节精度越高，但节流孔变长会使活塞的尺寸变大，从而会使整个关节尺寸变大。综合考虑精度与整体尺寸，取节流孔为宽2 mm、长5 mm 的矩形孔。根据主电机跟变阻尼电机的整体布局，曲柄滑块机构的偏距为40 mm，由于矩形节流孔的长度为5 mm，当曲柄滑块的行程达到最大时恰好为5 mm，起到对挡块限位的作用，如图2 所示。

图2 曲柄滑块机构示意图Fig.2 Diagram of crank slider mechanism

连杆L1与连杆L2的总长取80 mm，曲柄滑块的行程为5 mm，变阻尼电机的转动角度为θ。机构满足

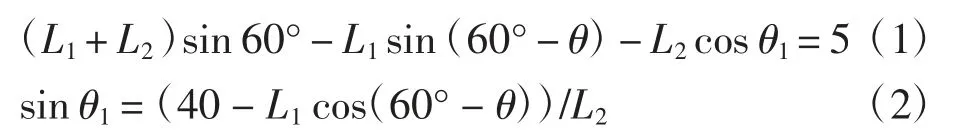
所选用变阻尼电机的最高转速为0.15 s/60°，要求变阻尼电机的响应时间小于0.1 s，因此变阻尼电机转动时，滑块应达到最大行程。由公式（1）、（2）计算取整，连杆L1可取20 mm，连杆L2为60 mm。

1.3 整体结构设计

根据上述关键零件的尺寸，对整个关节进行布局设计，如图3 所示。图3 中，变阻尼模块由变阻尼电机、曲柄滑块、滑环、挡杆、液压缸组成。缸体和活塞将液压缸分为4 个腔；活塞上有节流孔，活塞两侧腔内的液压油通过节流孔联通在一起。当活塞相对缸体旋转时，在活塞转动方向上的2 个腔体积被压缩，另外的2 个腔体积扩大，此时体积被压缩的2 个腔中的液压油会通过节流孔流向体积扩大的2 个腔中。活塞与输入轴通过花键固连在一起，构成关节输入端，主电机经过减速器减速将运动传递给输入轴；液压缸缸体与输出轴法兰固连在一起，构成关节输出端。

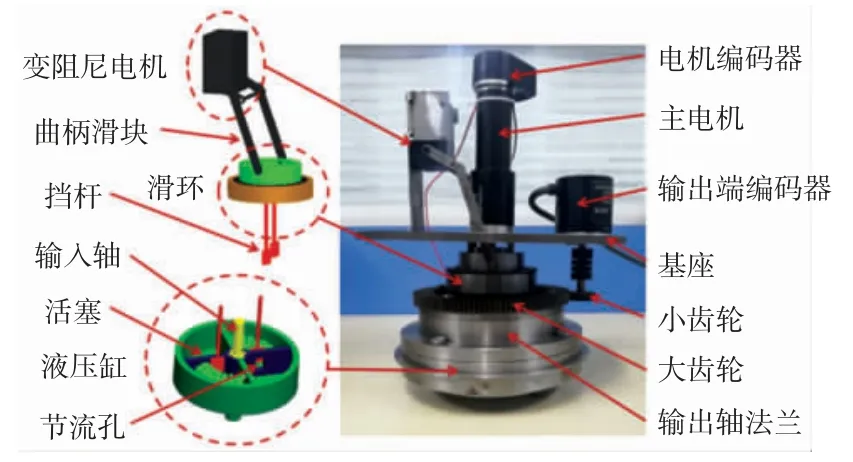
图3 变阻尼关节样机Fig.3 Variable damping joint prototype

输入轴缸盖上有2 个圆形通孔，挡杆由此通孔深入到液压缸中，可在通孔中上下移动以遮挡活塞上的节流孔。当挡杆向上移动时，节流孔开度增加，系统阻尼下降；当挡杆向下移动时，节流孔开度减小，系统阻尼增加。挡杆的另一端固连接到滑环上，滑环由上下两部分构成，通过轴承连接在一起，当上滑环上下移动时，下滑环可以围绕上滑环转动。滑环的作用是保证挡杆可以在活塞旋转时顺畅实现上下运动。上滑环是曲柄滑块机构的滑块部分。曲柄的另一端连接变阻尼电机。曲柄滑块机构将变阻尼电机的旋转运动转化为直线运动，即滑环和挡杆的上下运动，从而改变活塞上节流孔的通流面积。

为了保证天然柔顺性，本驱动器中集成了由2 个弹簧构成的弹性模块。弹簧一端连接在输入端，另一端连接在输出端。当输入端与输出端相对转动时弹簧将会发生形变，形变大小随着输入端与输出端相对运动的偏角的变化而变化。

驱动关节的主电机为Maxon 电机，变阻尼电机为伺服舵机。关节输入端和输出端的位置及速度由光电编码器测量，相对转动角度和相对运动速度可通过求差获得。

2 系统数学模型的建立与仿真分析

2.1 阻尼的计算与仿真

当主电机转动时，会带动活塞在液压缸内旋转，使液压油流经节流孔。活塞与缸体的相对转动速度和节流孔通流面积的变化，都会导致阻尼力的变化。

根据如图2 曲柄滑块机构的示意图，可以得到滑块在关节轴线方向上的位移

式中：L1、L2为连杆长度；e 为偏移距离；Δα 为变阻尼电机的偏转角度；α 为连杆L1在初始位置时与水平轴之间的夹角；β 为连杆L2在初始位置时与竖直轴之间的夹角；A 为初始位置时挡块到水平轴之间的距离。

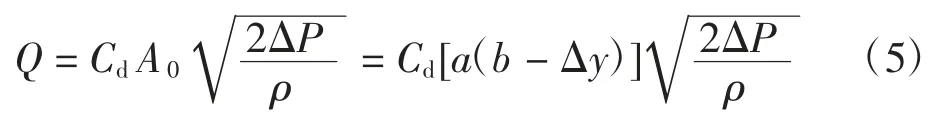
式中：Q 为流量；Cd为流量系数；A0为活塞孔的面积；a为节流孔的宽度；b 为节流孔的长度；ΔP 为液压缸两腔的压强差；ρ 为液压油的粘度系数。

由于活塞转过的体积与液压油流过的体积相同，所以

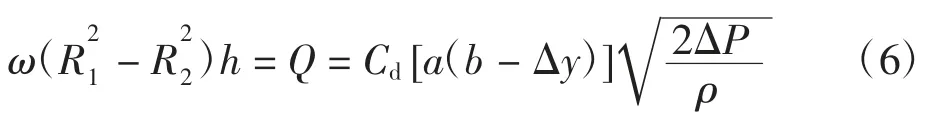
式中：ω 为活塞的角速度；h 为活塞的高度；R1为活塞的内半径；R2为活塞的外半径。

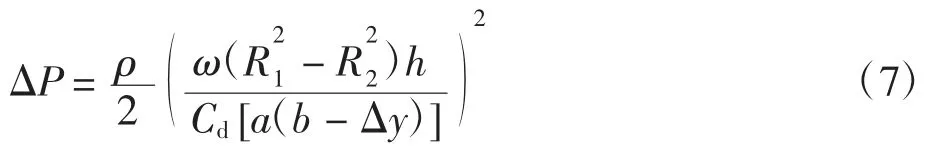
对活塞进行受力分析，阻尼力矩如下：

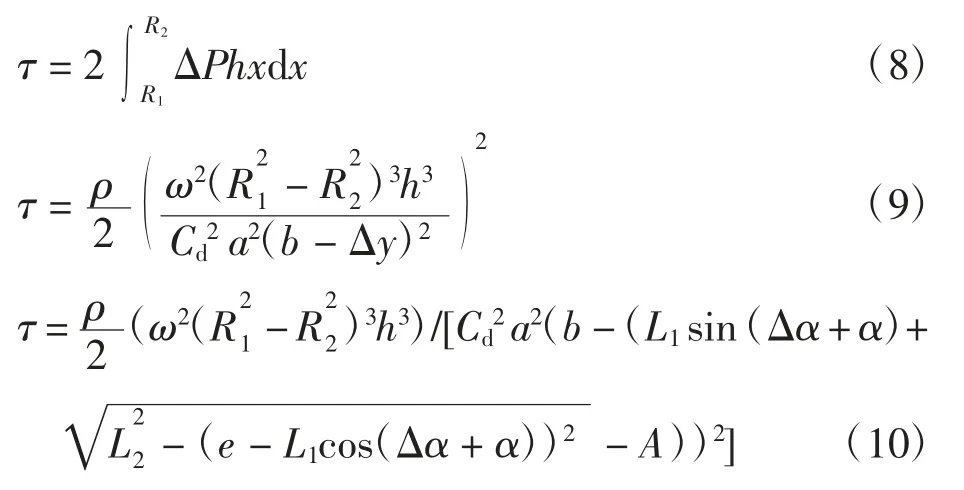
由此可见，阻尼力矩τ 与相对角速度ω、变阻尼电机偏转角度Δα 相关，且均为非线性关系。用Matlab对公式（10）变阻尼模块的数学模型进行仿真。图4 为当输入端与输出端相对转速不同的几种状况下，变阻尼电机的转角从0 逐渐增大，关节内阻尼力矩的变化。

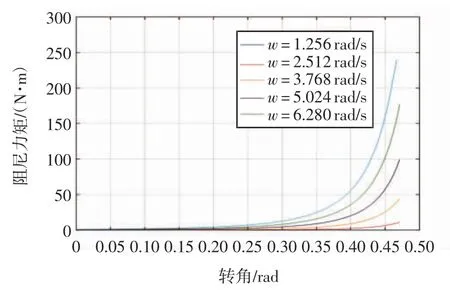
图4 阻尼力矩与变阻尼电机偏转角的关系Fig.4 Relationship between damping torque and deflection angle of variable damping motor

由图4 可知，阻尼力矩变化范围可达0～200 N·m，转角在0～0.35 rad 时阻尼力矩变化较为平缓且变化量不大，当转角大于0.35 rad 时阻尼力矩急剧增大。

由阻尼力矩计算公式（10）得出阻尼系数为：

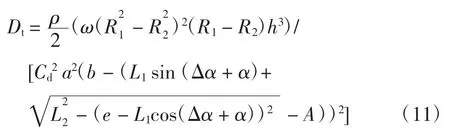
由式（11）可知，关节的阻尼系数Dt是变阻尼电机转角Δα 与相对速度ω 的二元函数。图5 为用Matlab对阻尼系数的仿真，显示了在 Δα 为 0～0.471 rad、ω 为0～6.280 rad/s 范围内关节阻尼系数的变化。

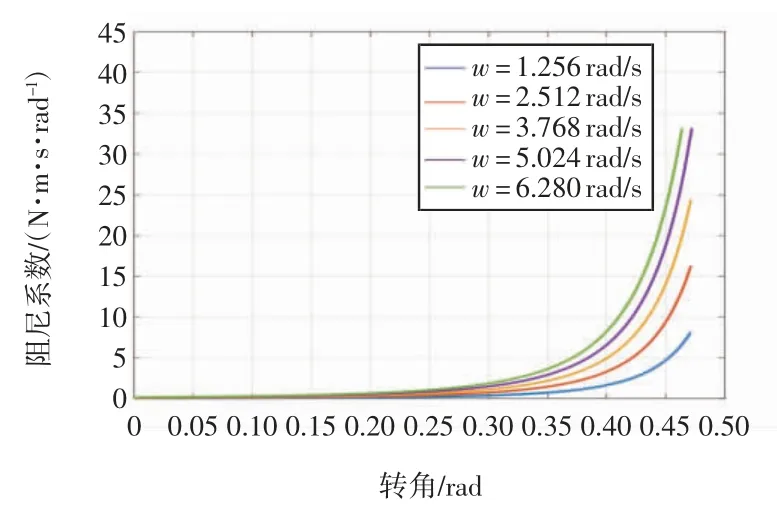
图5 阻尼系数与变阻尼电机偏转角的关系Fig.5 Relationship between damping coefficient and deflection angle of variable damping motor

由图5 可以看出，阻尼系数随着转角和相对速度的增加而增加，变化范围可达0～38 N·m·s/rad。当变阻尼电机偏转角小于0.35 rad 时，相对速度对阻尼系数的影响较小（0～4 N·m·s/rad）；当变阻尼电机偏转角大于0.35 rad 时，相对速度会显著影响阻尼系数（4～38 N·m·s/rad）。

2.2 系统动力学模型的建立与Matlab仿真

图6 所示为驱动关节模型，输入端与输出端除了弹性模块之外还有变阻尼模块。

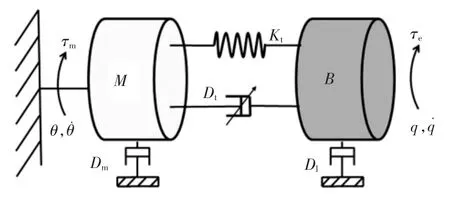
图6 驱动关节模型Fig.6 Drive joint model

图6 中，考虑输入端和输出端受到的阻尼，系统的动力学方程为：

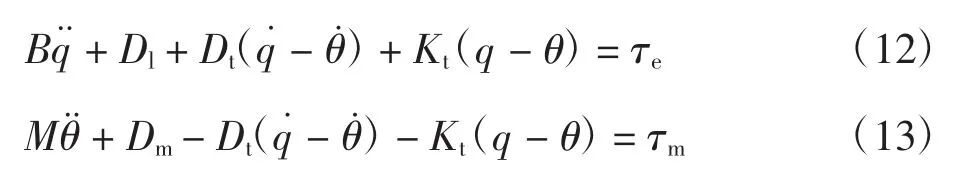
用Matlab 对动力学模型进行仿真分析，模型使用的参数值如表1 所示，在仿真中输入的信号τm为阶跃信号，负载τe为0，阶跃时间为1 s。在不同阻尼系数情况下，变阻尼关节的模拟结果如图7 所示。

表1 系统参数Tab.1 System parameters

由图7 可以看出，随着阻尼系数的增加系统的震荡减小，但过大的阻尼系数会导致更长的上升时间。当Dt=14 时系统在2.5 s 时还未达到稳定；当Dt=3时系统的动态性能较好，系统在0.5 s 内达到稳定。

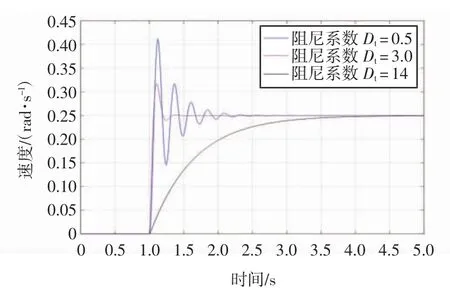
图7 不同Dt 下阶跃信号的速度响应曲线Fig.7 Velocity response curve of step signals under different Dt values

3 实验验证

3.1 实验平台的搭建

实验平台如图8 所示，包括变阻尼柔顺驱动关节、三菱PLC、主控计算机和电源。主电机的编码器测量电机轴的速度即输入端速度，输出轴法兰编码器测量输出端的速度，通过PLC 将信息传送给计算机。主控计算机通过反馈信息控制变阻尼电机改变阻尼，最终实现可变阻尼控制。

图8 试验测试平台Fig.8 Experiment test platform

3.2 控制策略

关节的控制单元包括2 个模块：第1 个模块采用经典的PID 算法和反馈回路来实现输出端的位置控制；第2 个模块调节变阻尼关节的阻尼系数，阻尼调节的主要目的是减少系统的振动，同时保持快速响应。增加粘性阻尼可以减少系统振动，但也会消耗更多功率并减慢系统速度。控制器框图如图9 所示。基于PID的闭环控制保证了系统的稳定性，而阻尼调节器提供可变的物理阻尼，以抑制主要由弹性部件产生的振动。

由图9 可以看出，阻尼系数是变阻尼电机角度和相对转速的函数，当相对转速发生改变时，要想维持阻尼系数不变就要改变变阻尼电机的转角。要想使变阻尼关节在不同速度下，维持在一个合适的固定阻尼值下就要控制变阻尼电机转角的大小，从而控制节流孔开口的大小。

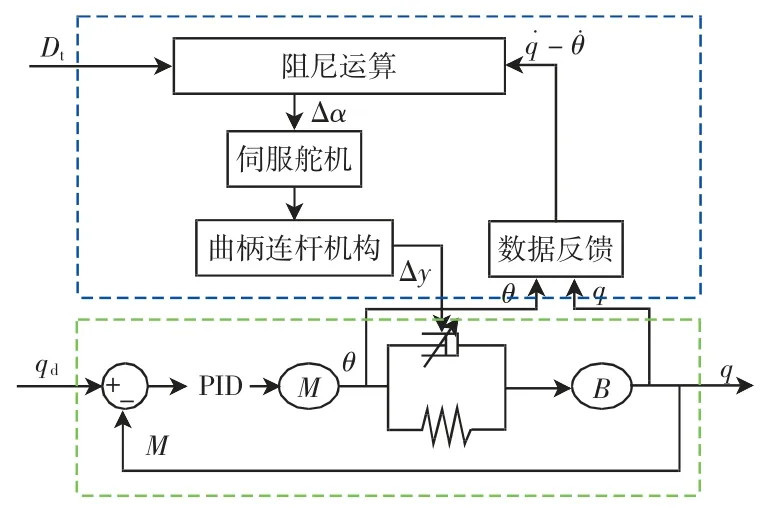
图9 控制策略框图Fig.9 Control strategy chart

3.3 实验结果

分别设置阻尼系数为0.5、3、14，变阻尼关节的位置跟踪性能如图10 所示。

图10 变阻尼关节位置跟踪图Fig.10 Position tracking diagram of variable damping joint

众所周知，弹性模块（本文关节原型样机中的弹簧）是将振动引入系统的主要因素。由图10 可以看出，如果阻尼系数设定为Dt=0.5，产生的粘性阻尼不足以抑制振动：如果阻尼系数设定为Dt=14，则振动完全消除，但系统的上升时间大大增加，2 s 时关节才达到稳定；当Dt=3 时，可以看到既有效抑制了振动又具有较快的响应，0.5 s 内关节达到稳定，且超调量减少50%以上。

4 结 语

本文设计了一种新型的变阻尼柔顺驱动关节，目的是减少传统柔顺关节的振动问题，且本设计直接采用流体节流原理实现了真正的变粘滞阻尼控制，当节流孔完全关闭时还可以实现自锁，使其变成刚性，无额外能量损耗。建立了变阻尼模块和完整关节的数学模型，分析阻尼力矩和阻尼系数的变化趋势，提出了一种双层控制策略，可以实时控制系统的输出位置和内部阻尼。试验结果表明：该变阻尼关节可以在保持令人满意的响应速度的同时减少系统的振动，当阻尼系数Dt=3 时，关节在0.5 s 内达到稳定，且超调量减少50%以上，动态性能良好。未来将要对不同形状的阻尼孔产生的阻尼特性进行研究，进一步使得变阻尼关节的结构更加紧凑，并将变阻尼关节应用于多自由度机器人系统。