基于神经网络的毫米波雷达与视觉传感器联合标定方法

牛萍娟，刘 雷

（1.天津工业大学 电气工程与自动化学院，天津 300387；2.天津工业大学 大功率半导体照明应用系统教育部工程研究中心，天津 300387）

在辅助驾驶（ADAS）中，基于毫米波雷达与视觉融合的车辆检测是重点研究方向[1-2]。为了获得毫米波雷达坐标系下一目标在图像像素坐标系下的坐标，需要进行毫米波雷达与摄像机的联合标定[3-4]。传统的标定方法是采用理想的小孔成像模型来模拟摄像机的成像过程初始化参数，然后通过非线性最小二乘法对参数进行修正，完成畸变校正[5-7]。毫米波雷达与摄像机的联合标定与神经网络都是建立一种映射关系，通过已有数据建立参数模型来对新的数据进行处理。在联合标定中，摄像机的成像模型是一种非线性模型，当采用非线性模型对摄像机进行标定时，需要使用非线性优化计算，但引入过多的非线性参数往往不仅不能提高精度，反而引起解的不稳定，而神经网络具有强大的非线性逼近能力[7-9]。所以，将神经网络应用于摄像机标定是可以实现的。

本文以基于毫米波雷达与视觉融合的车辆检测为背景，采用神经网络对毫米波雷达与摄像机进行联合标定，实时采集车辆目标数据，然后通过时间融合，将毫米波雷达信息与摄像机采集的信息进行对应，对采集的车辆目标进行标注，提取车辆目标的真实边界框中心点，将雷达极坐标系下的目标坐标R（目标径向距离）、α（目标方位角）转换为车辆坐标系后的坐标（xw，yw，zw）作为神经网络的输入，将经过标注的车辆目标真实边界框的中心点（u，v）作为神经网络的输出，采用反向传播和梯度下降算法来更新神经网络的参数，完成模型的搭建，并在测试集上进行验证。

1 传统联合标定方法

1.1 坐标转换过程

毫米波雷达的安装位置为车牌附近，摄像机的安装位置为车辆挡风玻璃处，而且都位于车辆中心轴线上，如图1 所示。图1 中坐标系（o0x0y0z0）、（owxwywzw）、（ocxcyczc）分别为毫米波雷达、车辆、摄像机坐标系。雷达距离地面高度为Hm，与车辆坐标原点距离为Lm，横向偏移为0；同理，摄像机距离地面的高度为Hn，与车辆坐标原点距离为Ln，横向偏移为0。

传统的雷达与视觉联合标定中，毫米波雷达的扫描平面为一个二维水平平面，如图2 所示，再确定雷达安装于车辆的位置，可将雷达测量的点转化为车辆坐标系中的某点。

图2 中，α 为目标方位角，R 为目标径向距离，o0为毫米波雷达安装位置。毫米波雷达坐标系与车辆坐标系转换关系如式（1）所示：

车辆坐标系下一点（xw，yw，zw）在图像像素坐标系下的坐标表示为（xu，yu），结合公式（1）可得它们之间的转换关系如式（2）所示：

以车辆中心轴线上的点为原点建立车辆坐标系，可以得到雷达的三维平移向量Tm=[0，Lm，Hm]，摄像机的三维平移向量Tn=[0，Ln，Hn]。由于其俯仰角、侧倾角和横摆角均接近于0°，借助车辆坐标系即可求取雷达与摄像头空间上的相对位置，可得式（3）：

所以，雷达和摄像机的坐标转换关系更新为式（4）：

1.2 摄像机内外参数标定

根据小孔成像原理，假定模板平面在世界坐标系Z=0 的平面上，[X Y 1]T为模板平面上某点的齐次坐标，[u v 1]T为图像上该点的齐次坐标，转换关系如式（5）所示：

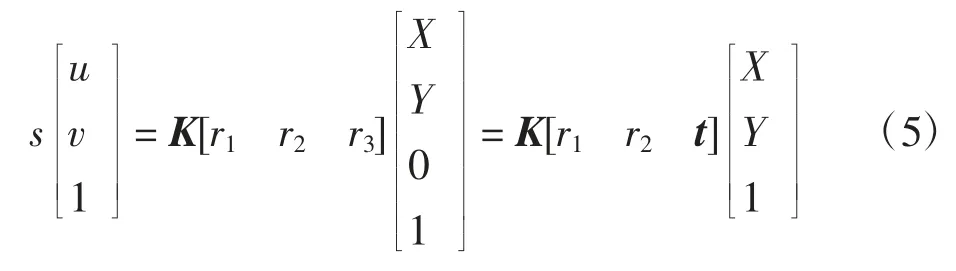
式中：K 为摄像机的内参数矩阵；[r1r2r3]和t 分别为摄像机坐标系相对于世界坐标系（本文即为车辆坐标系）的旋转矩阵和平移向量。

记单应性矩阵H=[h1h2h3]=λK[r1r2t]，每幅图像可以获得2 个对内参数矩阵的基本约束，如式（6）所示：

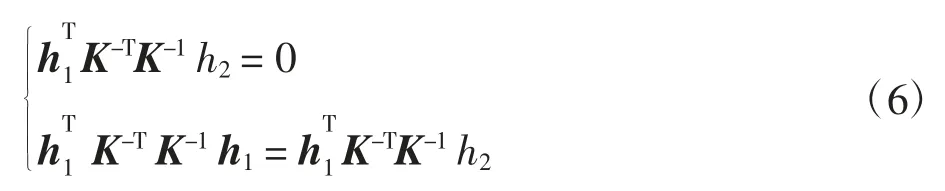
由于摄像机有5 个未知内参数，所以当拍摄到的图像数目大于等于3 时，即可线性唯一求解出K 值。

考虑到透镜畸变，参考坐标系从理想投影平面转换为实际投影平面，如式（7）所示：

式中：（x0，y0）为理想图像点坐标；（x，y）为畸变校正后的实际图像点坐标；r2= x2+ y2；k1、k2、k3为径向畸变系数。

由此可以看出，传统标定方法[10-12]的计算步骤繁琐，计算复杂度高，准确率低。为此，本文提出了一种基于神经网络的联合标定方法，以降低计算复杂度，并提高标定准确率。

2 基于神经网络的联合标定方法

本文采用了一种模型简单且具有良好泛化性能的BP 神经网络，BP 神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络[13-15]，主要包括输入层、隐含层和输出层，每层之间通过权重和偏差进行连接。理论上，含有一个隐层的三层BP 神经网络在隐层神经元节点数可以任意设定的情况下，能够以任意精度逼近任意连续函数。所以，本文采用三层BP 神经网络，如图3 所示。假设图3 中网络的输入特征向量为[x1，x2，…，xi]，输出为输入层与隐含层之间的权重为wih，偏移量为bh；隐含层与输出层之间的权重为whj，偏移量为bj。其中：i 为输入层神经元个数；h 为隐含层神经元个数；j 为输出层神经元个数。

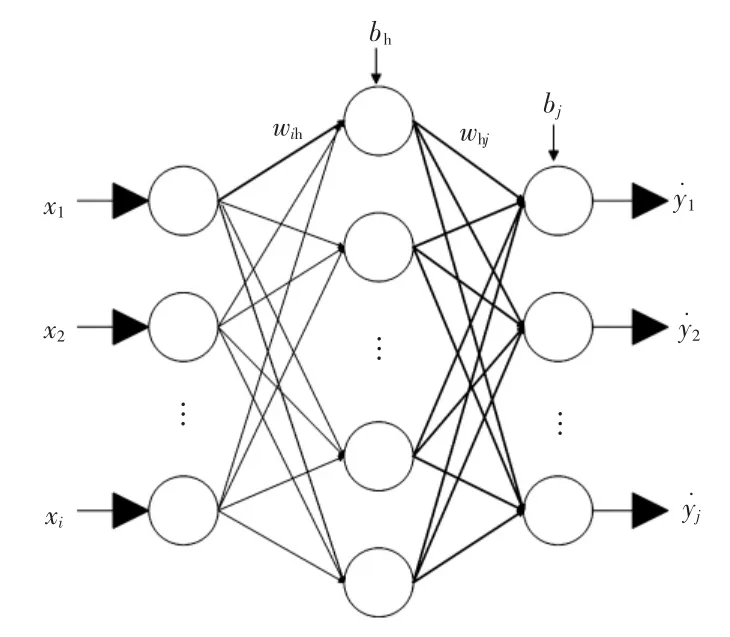
图3 BP 神经网络结构Fig.3 BP neural network structure

根据图3 神经网络的连接关系可知：

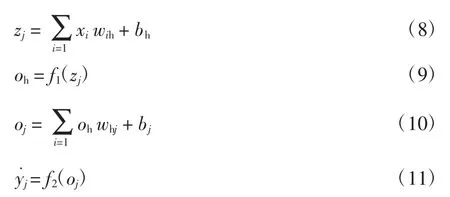
式中：oh、oj分别为第 2、第 3 层神经网络的输入；f1、f2为非线性激活函数，主要为了将神经元非线性化，从而实现非线性逼近。

误差函数采用平方误差函数，总样本的误差如式（12）所示：

利用梯度下降法使整体误差E 达到最小值，计算过程如式（13）、式（14）所示：

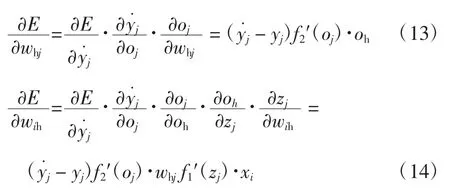
权值的更新规则如式（15）、式（16）所示：

本文采用一个三层的BP 神经网络模型进行标定，该网络由一个网络输入层（3 个节点）、一个隐含层（8 个节点）、一个网络输出层（2 个节点）组成，非线性激活函数选择ReLU 函数，权重w 采用均值为0、方差为0.01 的高斯分布进行初始化。如图3 所示，网络输入为目标在车辆坐标系下的坐标（xw，yw，zw），输出为目标在图像中的位置（u，v）。输入值为[xw，yw，zw]，输出值为[u′，v′]，真实值为[u，v]，总体误差如式（17）所示：

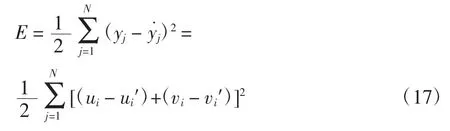
3 实验设计与仿真

3.1 实验数据获取

实验设备有：GEFORCE GTX1080Ti 电脑；维视MV-EM120C 型CCD 相机，最高分辨率1 280×960，像素尺寸 3.75 μm × 3.75 μm；湖南纳雷 CAR150 毫米波雷达。在目标检测中，需要定位出目标在图像中的位置，本文通过毫米波雷达和摄像机联合采集前方车辆信息，将毫米波雷达信息与图像上的车辆一一对应，然后对所采集的图像进行车辆目标的标定，取目标标定框的中心点作为目标物在图像中的映射。毫米波雷达数据采集通过上位机软件实现，可以得到目标物的径向距离R 和方位角α，转换到世界坐标系下即为神经网络的输入特征向量；车辆图像的数据标注结果如图4 所示，提取目标标定框中心点的图像坐标（u，v）即为神经网络的输出。

图4 车辆图像的数据标注结果和中心点Fig.4 Data annotation results and center points of vehicle images

张正友标定过程[8，16]中采用 5 × 7 的棋盘格，其内角点数为4×6，棋盘格边长为40 mm×40 mm，标定图片的数量一般在10～20 张之间，图像数量太少，会导致标定参数不准确，拍摄过程中要保证标定板的亮度足够且均匀，相机的光圈、焦距不能发生改变。根据以上分析，本文使用同一相机从不同的位置、角度、姿态拍摄12 张图像，如图5 所示。

图5 不同角度拍摄的标定板照片Fig.5 Photographs of calibration plate taken at different angles

3.2 实验结果对比

通过对采集的1 000 张图片进行标定，并提取目标中心像素坐标，将数据集划分为训练集700 个、验证集150 个和测试集150 个。该神经网络模型的训练、测试过程如图6 所示，可以发现，当运行50 个迭代后，测试集误差达到最佳的0.160 23。

图6 该神经网络模型的训练、测试过程Fig.6 Training，testing process of neural network model

不同方格标定板标定时，在X 轴和Y 轴方向上的像素误差如图7 所示。图7 中不同颜色表示不同角度的标定板对应的误差结果，红色的对应第2 幅标定板图像的误差较大。所有图片的像素误差err=[0.182 36 0.207 56]。

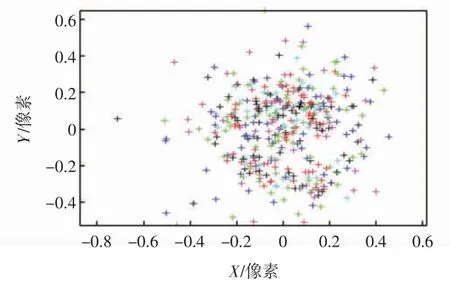
图7 不同方格标定板标定时在X 轴和Y 轴方向上的像素误差Fig.7 Pixel error in X-axis and Y-axis directions as different square calibration plates calibrated

采用张正友标定法得到的相机内部参数值如表1所示。两种标定方法的图像残差均值、总体误差和标定时间如表2 所示。

表1 标定得到的相机内部参数Tab.1 Internal parameters of camera obtained after calibration

表2 2 种标定方法的标定结果对比Tab.2 Comparison of calibration results of two calibration methods

将神经网络和传统标定方法重投影目标中心值的像素平方误差进行对比，部分结果如图8 所示。

图8 重投影目标中心值总体误差对比Fig.8 Comparison of overall error of reprojection target center value

传统联合标定方法中，相机内参的标定[17-21]是其中关键的一步，若相机内参标定误差较大，会使得毫米波雷达坐标系下的目标与其在图像像素坐标系中的投影位置出现较大的偏差，导致联合标定的误差较大，进一步影响车辆检测的准确性。通过表1 标定得到的相机内部参数值可以发现，经过畸变校正后，标定后的误差很小。若表1 中相机内参标定结果误差较大，会导致表2 中总体样本出现异常值，使得神经网络标定模型的泛化能力降低，标定过程中X 和Y 方向上的图像残差误差较大，方差也较大，会出现标定不稳定的结果，总体误差大，同时增加标定时间复杂度。由表2 可知，与传统标定方法相比，本文采用的神经网络方法误差低，方差小，且标定时间短。由图8 可知，本文提出的方法不仅标定精度高，且相对稳定，克服了传统标定方法过程复杂的缺点。

4 结 论

本文提出了一种基于BP 神经网络的毫米波雷达与摄像机的联合标定方法，并对其标定效果进行实验验证，结果表明：

（1）相机内参标定结果误差较大会导致测试集总体样本出现异常值，使得神经网络标定模型的泛化能力降低，标定过程中X 和Y 方向上的图像残差误差较大，方差也较大，会出现标定不稳定的结果，总体误差大，同时增加标定时间复杂度。

（2）用测试样本对所建立的神经网络进行泛化能力评估，其在验证集上的总体平均标定误差为0.160 89像素，时间为100 s，标定结果比传统标定方法精度高，且标定时间短，重投影后在X、Y 方向上的图像残差方差分别为0.001 8、0.002 1，具有很好的稳定性。该方法为辅助驾驶中的目标检测和跟踪等工作奠定了良好的基础。