改进ORB的轮式机器人视觉导航算法

成 怡，佟晓宇，朱伟康

（1.天津工业大学 电气工程与自动化学院，天津 300387；2.天津工业大学 天津市电工电能新技术重点实验室，天津300387）

轮式机器人自主导航的过程中，主要依赖自身携带的传感器感知周围环境，进行信息采集，完成目标任务[1-2]。通常，轮式机器人会工作在未知环境条件下，需要不断进行自身定位和建立环境地图，该过程被称为 SLAM（simultaneous localization and mapping，同步定位与地图创建）[3-4]，是目前移动机器人在未知环境下实现自主导航的核心算法[5-6]。

视觉传感器与SLAM 相结合可以更好地发挥出SLAM 技术的作用，视觉SLAM 技术在移动机器人中的应用日趋普遍。视觉传感器能够获取周围场景中的颜色、纹理和形状等环境信息，实现对周围环境场景的直观描述。特征提取算法的选择是视觉SLAM 算法实现的关键步骤，会影响轮式机器人视觉导航系统的实时性。目前，在机器视觉导航方法中的视觉SLAM算法里应用最为普遍的特征点提取方法有尺度不变特征变换（scale-invariant feature transform，SIFT）[7-8]、加速稳健特征（speeded up robust features，SURF）[9]和 ORB（oriented fast and rotated brief）[10]。但 SIFT 算法和 SURF算法在进行图像特征点提取时均要求建立高维描述符，需要占用大量的内存空间并耗费较长的运行时间[11]。因此，上述2 种算法不适合用于对系统耗时长短要求较高的视觉导航。

为满足轮式机器人视觉导航系统耗时长短的需求，本文运用图像特征提取算法中计算速度较快的ORB 算法，该算法的运算时间大约是SIFT 的百分之一，是SURF 的十分之一[12]。但是，通过ORB 算法提取到的特征点存在分布均匀程度较差和特征点重叠较多的弊端。因此，本文针对传统ORB 算法存在的上述缺点，提出一种改进ORB 算法，并设立基于区域统计方差数值的特征点分布评价方法，分析图像中特征点的分布情况。

1 基本原理

1.1 视觉SLAM算法基本原理

视觉SLAM 算法是实现轮式机器人机器视觉导航的核心。该算法的具体过程为：

（1）视觉传感器读取周围场景的环境信息，对获得的信息进行预处理，得到相应的点云数据或激光数据。

（2）利用视觉里程计部分估计相邻时刻图像间的位置关系，推算出当前时刻机器人的运动状况，还原当前场景的空间结构。在此过程中，会存在由估计形成的误差积累，即漂移现象[13]。此时，需要借助后端优化环节对此误差进行处理，后端优化可以对带有误差的数据进行整合，得到更为准确的数据结果。

（3）通过回环检测步骤识别机器人曾经到达过的地方，从而在后期数据处理的过程中舍弃重复的图像帧，减少计算量，消除累计误差。

（4）将移动机器人的运动轨迹和环境地图描述出来，实现轮式机器人的自主导航。

1.2 ORB算法的关键技术

ORB 算法可实现快速的特征点提取与描述，提高了运算速度，具备旋转不变性以及抗噪声能力。该算法中特征点的提取采用改进FAST 算法，即oFAST（oriented FAST）。改进后的 FAST 与原 FAST 算法[14]相比其每个特征点都有主方向，为后续使用BRIEF[15]生成特征点描述子具有旋转不变性提供了理论依据。特征点描述采用的是具有旋转不变性的rBRIEF（rotated BRIEF）算法，rBRIEF 算法采用了随机选点的机制，其主要思想是在特征点的周围选取一定数量的像素点，并比较它们对应的灰度值，通过比较一定数量的像素点对对应的灰度值的方法，可以有效地减少计算量，提高算法的运行速度。

1.3 ORB算法的特征点匹配

当对图像进行ORB 算法的特征点提取后，还需将提取到的特征点进行匹配，确定其对应的位置关系。

假设通过ORB 算法提取到的两帧图像中二进制特征点描述子的表达形式如式（1）所示：

利用式（2）对特征点描述子K1和K2进行异或处理：

计算结果 d（K1，K2）的值越大，证明相似程度越低。将计算结果按照数值的大小进行排序，其中，数值最小的点即距离最近的点为最佳匹配点。通过异或方法计算特征点描述子的匹配结果具有很高的效率。实际运用中，暴力匹配[16]总是尽可能地完成所有匹配，从中找到最佳匹配对。但是，会存在一些误匹配的情况，错误的特征点匹配会对轮式机器人的视觉导航产生干扰，得到的运动估计结果不准确。此时，需要使用RANSAC（random sample consensus，随机抽样一致）[17]算法对特征点做进一步的筛选。

2 改进ORB算法

在轮式机器人的机器视觉导航算法中，使用传统ORB 算法对待处理图像进行特征点检测与提取时，实验中提取到的特征点分布均匀程度较差，并且还会在图像中的某区域内发生特征点聚集的现象。为此，本文提出一种改进ORB 算法，建立尺度空间金字塔[18]，对每层图像的金字塔进行网格划分，用以增加空间尺度信息，增设网格行限制和列限制；特征点检测时，使用改进FAST 角点提取，设置感兴趣区域[19]，提高特征点提取精度；在计算Harris 角点响应部分时考虑角点邻域梯度；剔除重叠特征点时，采用非极大值抑制[20]方法，抑制Harris 角点响应的低阈值特征点输出。改进ORB 算法的流程图如图1 所示。

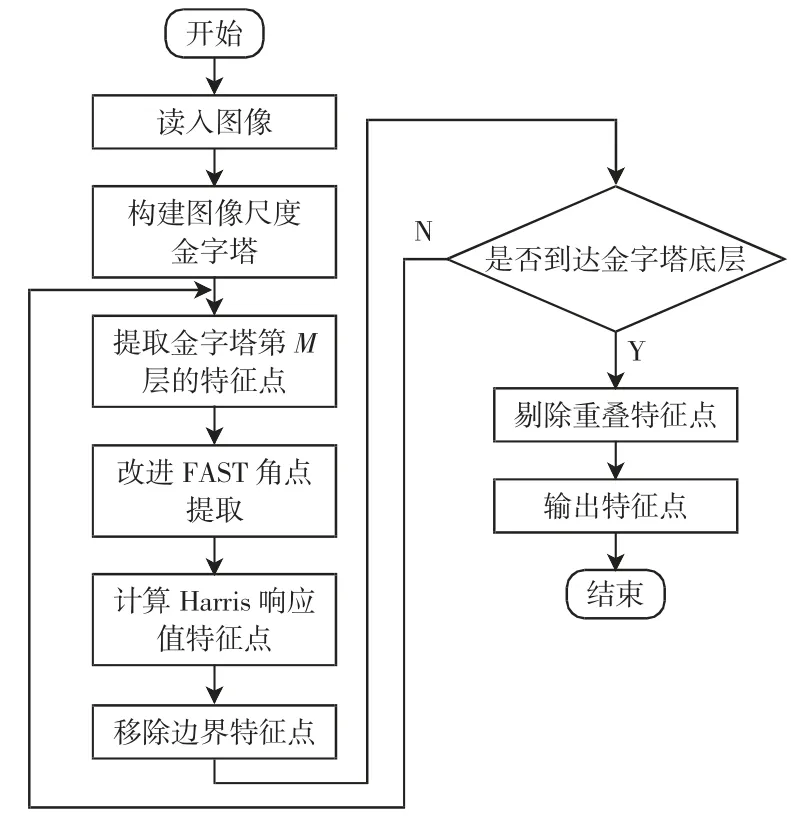
图1 改进ORB 算法的流程图Fig.1 Flow chart for improved ORB algorithm

2.1 改进FAST角点提取

感兴趣区域（region of interest，ROI）是图像处理领域经常用到的一个方法，它可以从图像中选择一个区域，使这个区域成为研究的重点。在改进的FAST 算法中，使用此方法，可以有效地减少系统处理的时间，提高特征点提取的精度。

改进FAST 角点提取流程如图2 所示。

图2 改进FAST 角点提取流程图Fig.2 Flow chart for improved FAST corner extraction

在改进的FAST 角点提取中，构建图像尺度金字塔，对该部分用到的所有参数进行初始化，并将高斯金字塔的每一层进行网格划分。增设网格行限制和网格列限制。图2 中：i 为行数；j 为列数；rows 和 cols 分别为每层金字塔分割的行数和列数。在FAST 角点提取过程中，需对图像进行边界处理，增设感兴趣区域；使用初始阈值对感兴趣区域内的特征点进行提取，并对较难提取到的特征点所在的网格部分采用先降低阈值再检测的方法，同时对特征点为空的情况设置了最小阈值，实现改进的FAST 角点提取；将所有提取到的特征点进行累积，并将已在感兴趣区域提取到的特征点的位置还原至已划分的网格区域中。

2.2 剔除重叠特征点

在特征点输出时，本文采用非极大值抑制的方法，用以提高特征点输出的质量，减少特征点在某些区域内出现的聚集重叠现象。该算法的本质是当出现多个待选结果值时，依照设定的目标条件对数据进行过滤，选出最适合的实验结果。以图像建立的尺度空间金字塔顶层为第1 层，选取在每层金字塔上都出现的特征点ai，ai∈A，A={a1，a2，…，ai}，ai=（xi，yi，εi）为已有特征点。对候选特征点bj（非每层均出现），bj∈B，B={b1，b2，…，bj}，bj={xj，yj，εj}。剔除重叠特征点的流程为：

Step1：特征点输出时，计算图像中现有的候选特征点bj所在的金字塔层上的某网格区域与已有特征点ai坐标之间的距离，并设置距离的临界阈值为l；

Step2：求解出候选特征点 bj={xj，yj，εj}与特征点A={a1，a2，…，ai}坐标之间的距离，选出距离≤l 的候选特征点 bj′={xj，yj，εj}；

Step3：计算Step2 中求出的距离值不超过l 的候选特征点 bj′={xj，yj，εj}的 Harris 角点响应阈值 εj′，根据候选特征点b={xj，yj，εj}响应阈值的激烈程度，即εj′数值的大小将这些候选特征点按照降序进行排列；

Step4：根据非极大值抑制算法的原理，将Harris角点响应阈值 εj′极大值所在的候选特征点 bj′ = {xj，yj，εj}保留下来，剔除其中的低阈值邻近候选特征点，得到特征点所在最佳位置的邻近特征点，实现降低重叠特征点输出的目的。

3 基于区域统计方差的特征点分布评价

图像特征点分布均匀性的评价主要用来估计特征点的数目在不同区域的图像内是否相同。如果特征点数量相同或者数量相近，说明图像中特征点分布的均匀程度较好；如果特征点的数量相差较多，说明图像中特征点分布的均匀程度较差。

鉴于上述评价方法，本文建立一个基于区域统计方差数值的特征点分布的均匀性评价方法。首先，将待检测特征点的图像按照垂直、水平、中心和四周、左上至右下、左下至右上的5 个方向对该图像进行区域划分[21]，得到上、下、左、右、左下、右上、左上、右下、中心和四周等10 个图像区域的方向；接着，按照以上划分方向对待检测图像内每一个区域的特征点数量进行统计，得到特征点在10 个方向上的数据值；然后，计算待检测图像中已划分的10 个区域中的特征点数量的平均值；计算待检测图像的特征点数量在已划分的10 个区域内的方差数值。从求得的特征点数量方差数值的大小关系可以推断出，特征点数量的方差数值越大，证明数据的浮动越明显，间接地反应图像中特征点分布的均匀程度较差；特征点数量的方差数值越小，证明数据的浮动越小，间接地反应图像中特征点分布的均匀程度较好。

4 实验结果与分析

本实验的操作平台是一款实验室自主研发的ROS[22]系统轮式移动机器人，其外观形状如图3 所示。

图3 实验室自主研发的移动轮式机器人Fig.3 Wheeled mobile robot independently developed by laboratory

该轮式机器人包括：视觉导航模块、上下位机通讯模块、底盘驱动模块、无线通讯模块等。系统操作环境为一台配置为i3 处理器、4.0 GB 内存的Ubuntu14.04的LINUX PC。程序运行时，配有Kinect1.0 深度摄像机的轮式机器人会以0.02 m/s 线速度、0.01 m/s 角速度采集实验室的全景图，实现轮式机器人的视觉导航。

4.1 图像特征点提取实验

为验证本文提出的改进ORB 算法的可行性，分别使用传统ORB 算法和改进ORB 算法对ROS 系统轮式移动机器人获得的彩色图像数据执行特征点提取环节，得到的特征点提取结果如图4 和图5 所示。

图4 图像特征点提取结果1Fig.4 Feature points extraction results 1

图5 图像特征点提取结果2Fig.5 Feature points extraction results 2

由图4 和图5 可知，经传统ORB 算法提取到的特征点分布效果不均匀，并且在某一区域特征点较为密集；而改进ORB 算法提取到的特征点分布整体较为均匀。实验结果表明，改进ORB 算法可以有效地实现特征点在检测图像上的均匀分布。

4.2 图像特征点分布实验

为进一步验证在对图像进行特征点提取时，使用改进ORB 算法得到的特征点分布均匀程度优于传统ORB 算法，采用本文提出的基于区域统计方差的图像特征点分布均匀性判别方法，求出特征点在图像中10个区域分布的方差数值，以此评价图4 的图像特征点分布情况，结果如表1 所示。

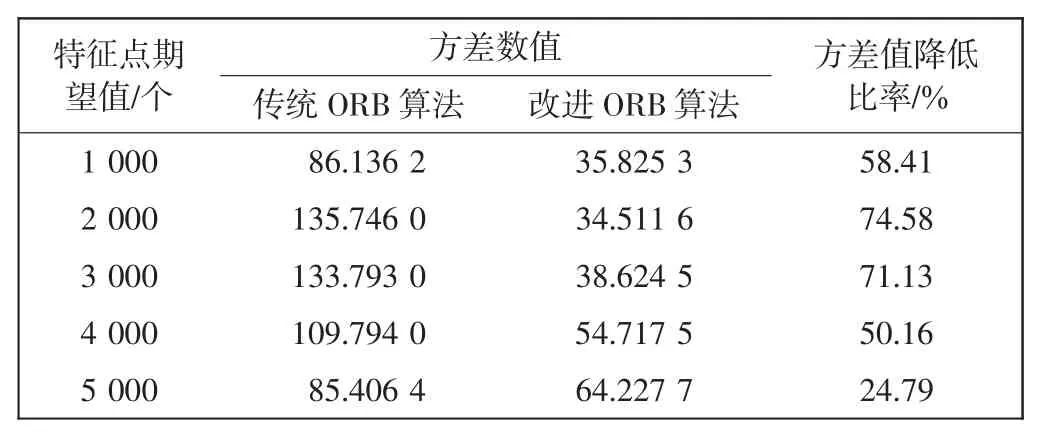
表1 不同算法中图像特征点分布均匀程度比较Tab.1 Comparison of uniformity of image feature points distribution in different algorithms

由表1 可以看出，随着特征点期望数量的增加，图像中特征点输出数量的方差数值及方差数值的降低比率也在发生变化；当特征点期望数量相同时，改进ORB 算法比传统ORB 算法的方差数值小，说明使用改进ORB 算法提取到的图像特征点分布的均匀情况较好。

4.3 图像特征点匹配实验

将使用传统ORB 算法与改进ORB 算法的特征点提取结果作为图像待匹配点，进行基于特征点的匹配实验。先使用暴力匹配结合hamming 距离的方法得到粗匹配，再使用RANSAC 算法消除粗匹配中的误匹配得到精匹配，结果如图6 所示。

图6 特征点匹配效果Fig.6 Feature points matching effects

由图6 可知，在进行特征点匹配时，由于改进ORB算法在特征点输出时，使用了非极大值抑制的方法对重叠特征点的阈值进行了处理，使其只输出某一范围中具有极大值阈值的特征点。并且，使用改进ORB算法获得的特征点分布情况较为均匀。因此，使用改进ORB 算法进行特征点匹配时，约束匹配点之间的线段分布较为稀疏，不会出现特别聚集的情况。

4.4 算法实时性分析实验

由于轮式移动机器人在进行视觉导航时对算法执行过程中消耗的时间长短有较为严格的要求，本文分别使用传统ORB 算法与改进ORB 算法对图4 在算法执行步骤中的特征点提取与匹配环节所消耗的时间进行对比，实验结果如表2 所示。

由表2 可以看出，当设置的特征点期望数值越大时，算法执行特征点提取与匹配消耗的时间就越长；当期望特征点的数量设置一致时，从算法执行时间的角度来看，同一张图像使用改进ORB 算法进行特征点提取与匹配时消耗的时间少于传统ORB 算法，说明改进ORB 算法耗时较少、实时性较高。

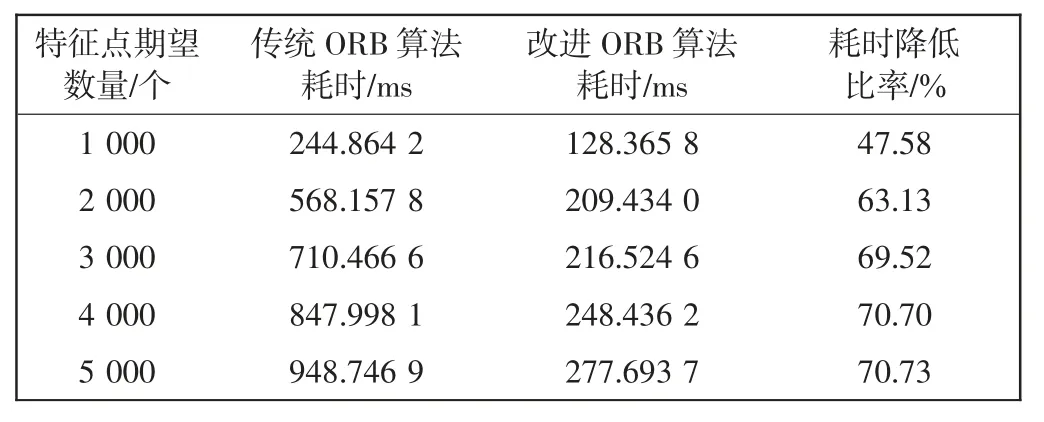
表2 ORB 算法的实时性分析Tab.2 Real-time analysis of ORB algorithm

5 结 语

针对传统ORB 算法存在特征点分布均匀程度较差、耗时较长的缺点，提出一种改进ORB 算法，并将该算法应用于实验室自主研发的轮式移动机器人进行机器视觉导航。对传统ORB 算法中的FAST 角点提取环节使用改进的FAST 角点提取方法；在特征点输出部分，采用非极大值抑制的方法有效地减少低阈值特征点的输出数量，避免特征点在某一响应区域内重叠地出现在检测图像上；为了便于解释图像中特征点的分布均匀程度，提出一种基于区域统计方差数值的图像特征点分布均匀性的评价方法。实验结果表明，当特征点期望数值设为3 000 时，与传统ORB 算法相比，改进ORB 算法的图像特征点分布均匀程度提高71.13%，耗时降低比率为69.52%，可以更好地应用于轮式机器人执行视觉导航算法中。