股票市场各行业流动性溢出效应分析

(四川大学经济学院 四川 成都 610065)

金融市场要正常运行，良好的流动性是基础，如果金融市场的流动性出现问题，金融市场就不会健康发展，甚至可能会崩溃。因此，对我国股票市场各行业进行流动性的溢出效应研究对风险的防范是有一定意义的。

一、股票市场的流动性测算和向量自回归模型

(一)流动性指标建立

从以往流动性定义中发现，速度、价格、交易量[1]是度量的重点。在Amihud(2002)提出的流动性比率，即Lt=(lnPt-lnPt-1)/Vt(其中Pt为第t日的收盘价，Vt表示第t日的交易额)基础上加入交易当天的最高价、最低价和收盘价，即Lt=|ln(max{Pt-1,Mt-1})-ln(min{Pt-1,Nt-1})|/Vt(Lt是第t日流动性指标，Mt是第t日交易最高价，Nt是第t日交易最低价)。Lt是描述单支股票的，为度量一个行业，Kee H.Chung(2014)将每天的流动性按当天股票的市值权重加权加总后得到平均流动性[2]。类似地，行业的流动性指标为：Mt=∑i∈IWit×Lit(Wit为第i支股票第t天的市值权重，Lit为第i支股票第t天的流动性)

(二)向量自回归var模型

对变量Y1，Y2，…，Yk的滞后p期的VAR模型有：

Yi,t表示第i个变量在第t时刻的值，μi1表示常数项，βij,m表示滞后j期时变量Xm的系数,εt表示随机扰动项，它们之间可以同期相关但不与自身滞后项相关。

二、实证分析

(一)数据处理

第一，按WIND数据库划分的11个一级行业分别为材料、地产、电信、工业、公用事业、金融、可选消费、能源、日常消费、信息技术和医疗行业(本文用首字母大写替)，对2012年1月4日到2017年11月17日的日数据按上文方法计算各个行业流动性指标，最终得到11个时间序列。数据均来源于Wind数据库。

第二，检验序列平稳性，采用ADF单位根检验各时间序列是否平稳。结果表明所有的变量在5%的显著性水平下均具有平稳性，因而可直接建立VAR模型。

第三，确定滞后阶数，通过建立不同滞后期的VAR模型，得到不同的LR,AIC和SC。SC准则显示最优滞后长度为2，AIC准则和LR准则都显示最优长度为20。确定阶数一般根据AIC和SC取值最小准则，最后选择最优滞后阶数为2。

第四，格兰杰因果检验。首先检验VAR模型稳定性，结果显示AR根全部在单位圆内，说明估计的VAR(2)是稳定的，然后进行格兰杰因果关系检验，若某一变量不存在与其他变量的格兰杰因果关系，则是外生变量。结果表明无外生变量。

(二)流动性溢出的脉冲响应分析

运用VAR模型的脉冲响应函数可以分析一个行业流动性受到冲击时，其他行业的流动性的变化。以材料行业为例，材料行业对来自材料、地产、金融、工业的冲击做出的反应较大(top4)(图1)，当给与各个行业流动性一个正向冲击，材料行业对本行业冲击的反应最大，并在第二期迅速减弱，第十期后缓慢减弱，对地产行业的反应次之，先正向反应，再逐渐趋于平稳，对金融行业冲击的反应排第三，对工业的冲击反应更弱。

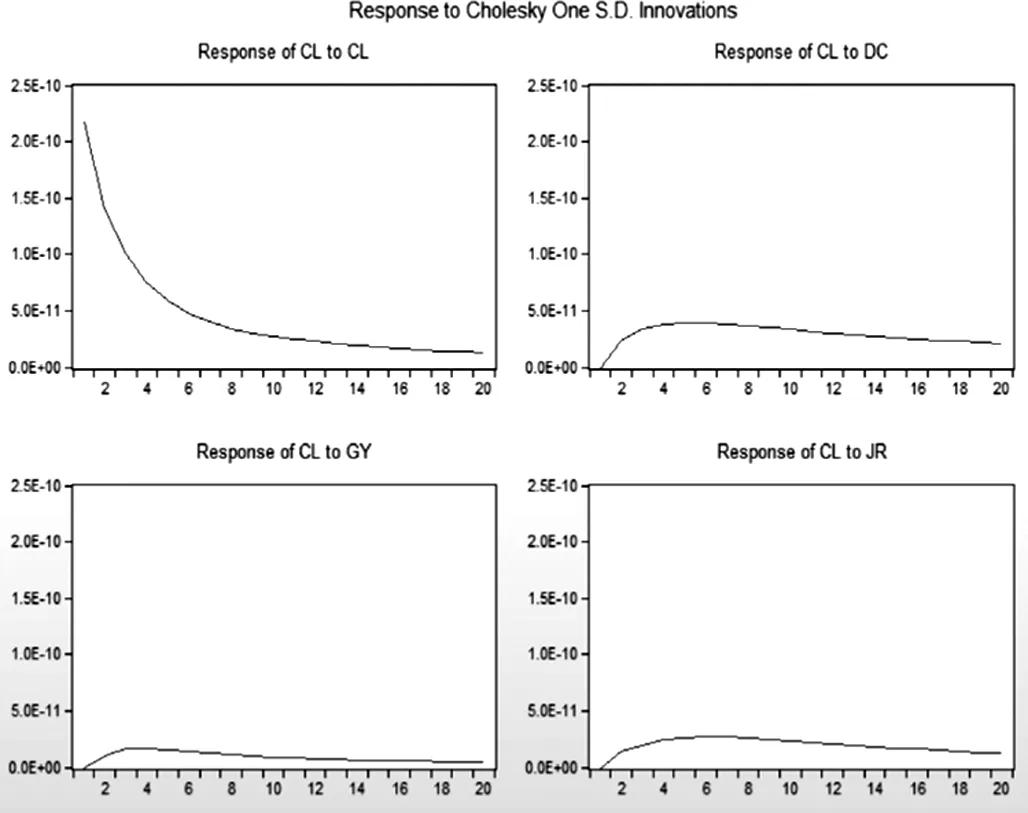
图1

同理，按照以上方法，归纳得表1。

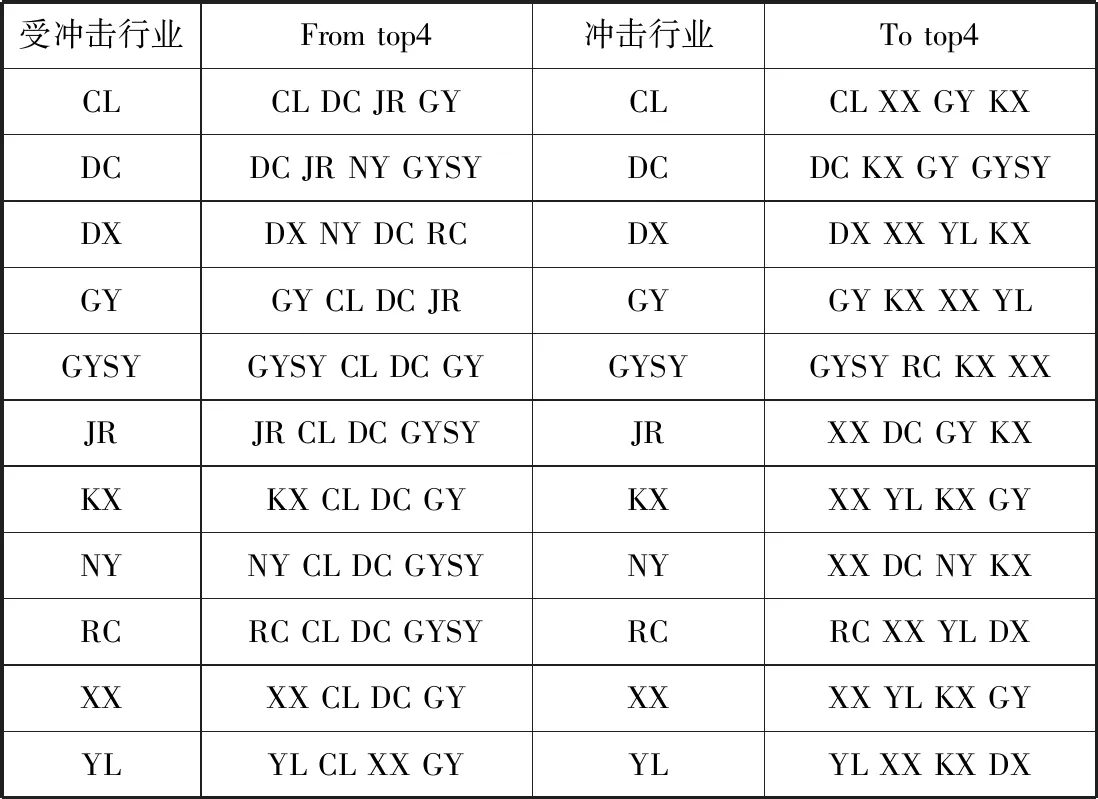
表1 脉冲相应大小

三、结论与启示

本文主要从流动性溢出的角度分析行业之间的相互影响。通过建立VAR模型发现各个行业流动性变化对其他行业的流动性都有或大或小的影响。在整个样本期内，11个行业的系统中各行业流动性溢出效应非常明显。就流动性溢出角度来看，房地产行业对其他行业流动性的影响最大，在同期的流动性传递网络中，房地产行业对除医疗外的十个行业均具有显著的溢出效应。这也证实了房地产行业作为基础性行业，与其他行业都有较紧密的联系，房地产行业股票流动性的变化会给整个股票市场带来影响。材料行业和金融行业的溢出效应次之。就流动性接收角度来看，信息技术行业对来自除了地产行业外的其他行业冲击的反应均排在前四位，说明信息技术行业是最容易受到其他行业流动性溢出影响的，医疗卫生和工业行业次之。

从研究流动性溢出的过程和结果中对我国防范系统性风险有如下启示。第一，防范系统性风险不应仅关注于金融体系，而应放眼于整个市场行业网络。良好的流动性是保证金融市场正常运行的关键，在防范流动性风险时应依据系统重要性程度进行差异化监管。第二，要特别关注系统中重要性极高的行业，例如大部分时期内的房地产行业，可以被认为是系统性流动性溢出的源头，处于“太关联而不能倒”的地位，应做好前瞻性的调控。