100倍圆法和角规测定林分株数密度的性能对比分析

刘明星，鄢前飞，李明诗，3

（1.南京林业大学 林学院，江苏 南京 210037；2.中南林业科技大学 林学院，湖南 长沙 410004；3.南方现代林业协同创新中心，江苏 南京 210037）

林分每公顷株数是反映林分生产力和健康状态的一个重要因子，直观反应林分的空间利用状态[1]。造林、营林、林分调查及编制林分生长过程表或收获表都充分依赖于这一密度指标。同时，株数密度[2]指标直接反映了每株林木平均占有的林地面积和营养空间的大小。

目前林分株数密度的基本方法是标准地法[3-7]，这种方法的核心是以有代表性的有一定面积地段的林木数量来推算林分每公顷株数。标准地法通常是用每木检尺来完成，这样不仅可以估算林分每公顷株数，同时还可以分析林分直径株数结构及分布规律[8-9]。

除了标准地林分株数密度的测定方法，森林调查实践中还采用了角规方法测定林分株数密度。另外，鄢前飞提出了林分平均直径100Dg 圆这种方法来测定林分株数密度[10-12]，蒙彬在此基础上进行了林分平均胸径 100Dg 圆公式在随机抽样中的理论论证[13]，孙丽娟进行了100Dg 圆法与角规、标准地法测树特征的对比分析[14]。但是以上学者都只是停留在理论研究阶段，至于实践应用与测试还未见报导。本文旨在对比常规的角规测树法与林分平均胸径100 倍圆法测定林分株数在精度、野外测量效率等方面的差异，为森林调查方法选择提出初步推荐方案。

1 研究区概况与研究方法

1.1 研究区概况

实验研究地位于湖南长沙县大山冲森林公园。该公园属湖南省省级森林公园，位于长沙县东北的路口镇境内，地处28°02′58″～28°24′58″N，113°17′31″～113°19′08″E。土 地总面积为419.4 hm2。该区域属中亚热带湿润大陆性季风气候。总的气候特征是：气候温和，热量丰富，降水充沛，日照充足，四季分明，无霜期长。

1.2 研究方法

角规测定林分每公顷株数的方法是：在林地内随机设置一个样点，观测者以样点为中心，用水平角规依次绕测周围林木的胸高部位一周。当林木胸高断面与水平视角相割时，即为抽中的样木，并予以计数1。当林木胸高断面与水平视角相切时,即为抽中的样木，并予以计数为0.5。当林木胸高断面与水平视角相离时，不予以计数。所有计数之和即为绕测计数[15]。为求得每公顷林木株数n，需测定每株计数木的直径实测值和所属径阶，然后根据某径阶中值的断面积gi 和角规断面积系数以及某径阶计数木株数测定出某径阶的每公顷株数，林分每公顷株数即为全部径阶所推测的株数的累加值[16]。

另外一种测定林分株数密度的方式是林分平均直径100 倍圆法（简称100Dg 圆法）。所谓100 倍圆法是以林分平均胸径的100 倍为直径作圆形样地，则林分每公顷胸高断面积刚好等于圆形样地上圆内的林木株数加上圆界上林木株数的一半。100 倍圆法是一种新的测量林分每公顷胸高断面积的方法，其测树的基本准则归纳如下：

1）当树木至圆心E 的水平距离L=50Dg 时，树木为圆界木，计为0.5 株。

2）当树木至圆心E 的水平距离L＜50Dg 时，树木为圆内木，计为1 株。

3）当树木至圆心E 的水平距离L＞50Dg 时，树木为圆外木，不计数。

在100 倍胸径圆内达不到林分起测径阶（一般在5 cm 以下）的树木视为幼树，圆内木与圆界木是指符合检尺范围的林木。设圆内木总株数为n，圆界木总株数为m，则胸高断面积G=n+m/2[11]。

在湖南省长沙县大山冲森林公园进行了马尾松[17]、杉木2 种林分类型共12 块试验样地的野外测定。各实验样点均釆用典型选样，分别开展100倍圆法与角规对照实验，两种方法要求定点保持一致性，计数木都控制检尺。此次使用的测距工具具有我国自主知识产权的深达威公司生产的室外型手持式激光测距仪，型号为SW-50A,测量距离为50 m，测量精度为mm 级。

以试验区样点1 为例，具体方法及步骤如下：

在杉木大径材林分试验样点500 m，选择好有代表性地段作为典型选择地，然后在此地段上设置好观察的圆心点，定点用木桩做好明显标志。此点即是100 倍圆法点，也是角规观察点。

目测林分平均胸径以及林分最大直径。在圆心附近地段范围，采用目测方法快速获取林分平均胸径目测值（dg 目）。目测方法是选出大体按中等大小的树木3～5 株，实测其胸径，以计算其平均值作为林分平均胸径目测值。同时目测出林分最大直径并量测其值。1 号样点得出目测平均直径32 cm，最大直径45.6 cm。

以最大直径为参考，作大圆形标准地。本次根据最大直径45.6 cm 为参考，圆形标准地的半径综合确定为25 m，大圆形标准地的面积25 m×25 m× 3.14=0.196 25 hm2。大圆形标准地的每木检尺所测算的每公顷断面积与每公顷株数视为100 倍圆法与角规所测的每公顷断面积与每公顷株数的“真值”参照值。

在圆心点上分别进行大圆形标准地的测量，100 倍圆测量和角规测树工作。大圆形标准地的测量测树方法是：一人手持激光测距仪在圆心点认真按25 m 为准值进行大圆形标准地的圆内木、圆界木水平距离的测量，若超过25 m 在圆外的圆外木不测量。100 倍圆测量以16 m 半径为判别依据进行圆内木、圆界木的判别，角规测树对于判别不清林木相切、相离还是相割时一律釆用临界距公式，3 种方法都涉及到水平距离测量。另一人负责数据外业记录。第3 人负责标准地的每木检尺[18]与100 倍圆及角规控制检尺工作。

2 结果与分析

2.1 第1 号样点结果与分析

2.1.1 外业调查表

1 号杉木试验区外业调查表如表1。

表1 第1号杉木试验点25m半径圆标准地的外业调查结果Table 1 Field survey results of the Chinese fir circular sample plot No.1 with a radius of 25 m

上表统计总株数n=110 株，最大圆半径为25 m，林木最大直径为45.6 cm，最小直径18.1 cm。

2.1.2 每公顷胸高断面积、平均直径、每公顷株数的计算

利用Excel 计算样木均方直径和为114 897.17，平均直径为32.3 cm，标准地各样木断面积和为9.024 002 m2，按标准地面积1 963.495 m2，推算出林分每公顷胸高断面积为46 m2。每公顷株数为560 株，以此胸高断面积为46 m2，每公顷株数为560 株作为本次100 倍圆法及角规的“真值”，作为100 倍圆法及角规的精度计算的参照。

2.1.3 25 m 半径圆形标准地的林分直径结构

25 m 半径圆形标准地林分每公顷株数以及直径结构分布如下表2及图1所示。

从表2及图1可见，此林分每公顷株数为560株，径阶分别从18 径阶分布至46 径阶呈连续性分布，且近似呈现正态分布。其中以平均直径32径阶为中心左右3 个径级（左26、28、30 径级，34、36、38 径级）左右近似对称，本标准地基本合乎同龄林直径结构分布规律。

表2 第1号杉木试验点标准地林分每公顷株数及直径结构分布Table 2 The per hectare stem number and corresponding diameter structure distribution derived from Chinese fir sample plot No.1

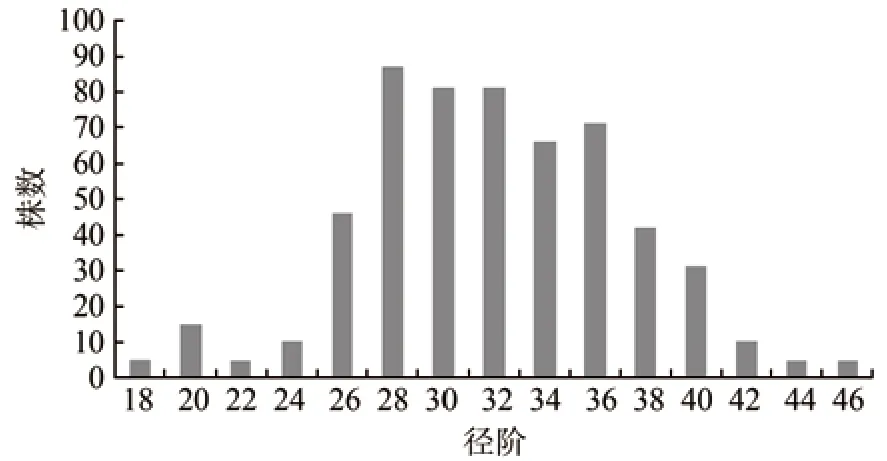
图1 大圆形标准地每公顷株数分布Fig.1 Distribution of the per hectare stem number in the circular sample plot No.1

2.1.4 100 倍圆法推算每公顷株数及林分直径结构

本文以林分平均直径100 倍圆径阶及计数木株数按面积比例算推算统计林分每公顷株数以及直径结构，见表3。

对比表3与表2可知，100 倍圆法林分每公顷株数推算值为500 株，估测精度为89.29%。整个估测径阶分布基本上连续，大体呈现近似正态分布，其中平均直径32 径阶为中心左右3 个径级(左26、28、30，右34、36、38 径级)近似对称。用100 倍圆法推算林木各径阶的株数也大致合乎同龄林直径结构分布规律。

2.1.5 角规推算每公顷株数及林分直径结构

以角规径阶按计数木株数与径阶推算统计林分每公顷株数以及直径结构，基本信息如表4所示。

表3 100 倍圆林分每公顷株数及直径结构分布Table 3 Per hectare stem number and diameter distribution derived from the 100 times circle method

比较表4和表2可见，角规林分每公顷株数推算值为465 株，估测精度为83.04%，估测径阶基本连续，左偏多，对连续性径阶序列有影响，但也大致符合正态分布。可见，用角规推算林木各径阶的株数大致可以反映同龄林直径结构分布规律。

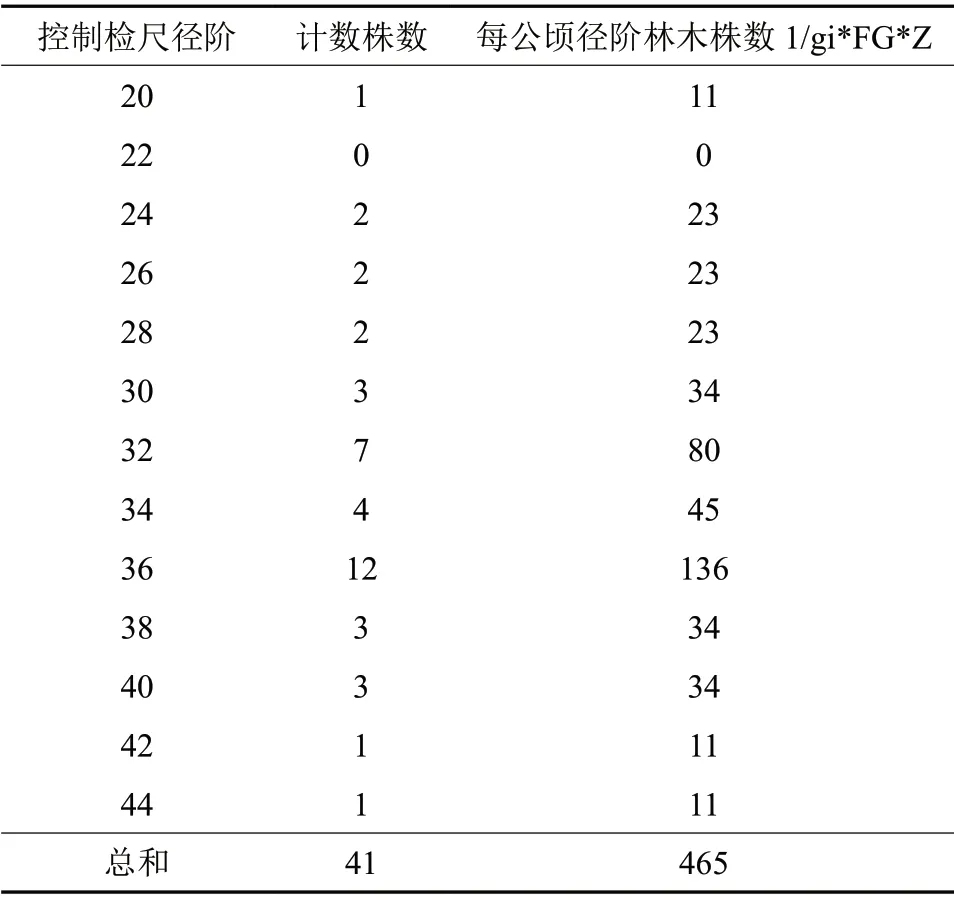
表4 角规林分每公顷株数以及直径结构分布Table 4 Per hectare stem number and diameter distribution derived from the angle gauge method

2.2 全部样点结果汇总与分析

将12 个样地外业调查结果进行分析汇总，统计信息如表5所示。表6计算出了2 种方法在每公顷断面积与每公顷株数的估测精度。

表5 各样点2种方法每公顷断面积与每公顷株数估测Table 5 Estimates of the per hectare basal area and stem number derived from sample plots using two different methods

表5和表6显示，100 倍圆法断面积估测的平均精度为90.17%，角规断面积估测的平均精度为87.99%，100 倍圆法断面积估测的平均精度略高于角规约3 个百分点。100 倍圆法测定每公顷株数的平均精度为92.28%，角规每公顷株数测定的平均精度为86.84%，100 倍圆法测定每公顷株数的平均精度略高于角规约6%。利用Excel 计算，100 倍圆法的估测精度的方差为0.1%，角规测树法的估测精度方差为0.4%，远优于100 倍圆法。100 倍圆法的波动性更小，估测精度更稳定。利用Excel 进行差异显著性分析，F=5.507 818，Fcrit=4.351 244，F＞Fcrit，则两种方法估测每公顷株数的精度在α=0.05 的水平上有显著差异。

表6 各样点2种方法每公顷断面积与每公顷株数的估测性能Table 6 The per hectare basal area and stem number estimation performances developed from the 100 times circle and the angle gauge methods within the sample plots

3 讨 论

100 倍圆法相对角规方法而言在无论是在推算每公顷株数精度方面还是在直径结构分布方面都具有优势，同时测量效率方面也更高一些。

在株数精度方面，普通角规测树时，光线的强弱和来光的方向对观测结果有一定的影响。如光线较弱或光线从观测者背后照来，会把略大于缺口的树看成为相切树，或把相切树看成为小于缺口的树，从而使观测值偏小[19]。角规测树法需要注意测器接触眼睛一端，必须使之位于角规点的垂直线上；角规点不能发生位移；角规断面积系数的选择；坡度改正；认真确定临界木等因素。如角规系数[20]的选定问题，角规系数F 越大，视角也越大，则被计数株数少，弄错一株对结果影响很大；视角越小，则观测距离越远，肉眼观测的误差也大，漏测和错测的机会增多，降低精度。100 倍圆法是根据距离来判别，没有那么多要求，专业性不强，操作起来更加容易[14]。另外100Dg圆法为具体的、简明的、有边界的、小范围有形样地，每公顷株数的测定和径阶的株数的测定是根据圆的面积按比例来推算的，这样，相对保持了典型样圆的胸径分布特征和林分总体分布特征的一致性和合理性。而角规是比较抽象的、大范围的无形样地，相切树木、相割树木、相离树木往往是“犬牙交错”的，角规就难以反应林分总体分布特征的一致性和合理性。

在测量效率方面，本次试验均采用激光测距仪测量距离，更加高效精准。100 倍圆法与角规法效率相差不大，100 倍圆法相对快一些，原因如下：1）在林木观察对象上，角规测树是通过若干株林木大范围“搜索”并按照是否相切、相割、相离这一“逐一判断”与“取舍”的法则来确定计数株数以获取林分断面积估测数据的。角规直接测量距离即可计数。2）角规一般要求正反绕测两次以相互检查是否重测或漏测，而100 倍圆法是集中在样圆内，方便做标识与编号，不易漏测和重测，基本上可以做到绕测一周一次性完成。3）角规测树操作过程中对判断不准的树木要求实测胸径和树木至观察者的距离这两个因素，然后采用临界距公式来判断是否相切、相割、相离[20]，而100倍圆法却省略了这些环节，直接测树木至圆心的水平距离进行单因素判断。这些因素使得100 倍圆法测量效率更高。

本研究由于时间有限，只是对同龄林[21]作了研究，而对异龄林没有开展研究，以后有待于加强原始林、次生林这方面的100 倍圆法的测定林分每公顷株数的精度应用性研究。同时，100 倍圆法也有一定的局限性。它首先需要通过一种方法（一般是目测法[5]）快速而准确地估测林分平均直径，这要求调查者对林分全局判断严谨并有一定的测树经验[15]。激光测距仪相对角规造价昂贵，还没有在测树工作中普及。

4 结 论

以 100 倍圆推算的林分每公顷株数在具体直径分布上基本上呈径阶的完整性与连续性，并且大体和标准地类似呈现近似正态分布，其中以平均直径的径阶为中心轴呈现左右3 个径级的左右近似对称图形，100 倍圆法推算林木各径阶的株数大致合乎同龄林直径结构分布规律。100 倍圆法测定每公顷株数的平均精度略高于角规约6 个百分点。两者在每公顷株数测定上都取得了比较满意的效果，相对而言100 倍圆法测定每公顷株数精度稍微略高一点，同时测量效率方面也更高一些。由于林分平均直径100 倍圆法来测林分每公顷胸高断面积的精度高的前提下，100 倍圆法推算每公顷株数也比较高，但这种方法目前还没有得到广泛应用，因此，该方法具有很大的发展空间并且可以在林业上普及、推广。