星球车非结构化环境行驶稳定性分析

刘 涛，肖建军，唐 玲*，魏世民

(1.北京邮电大学自动化学院，北京100876；2.中国载人航天工程办公室，北京100094)

1 引言

星球表面沙石遍地，沟壑纵横，具有山丘、丘陵、山脉、火山、陨石坑等多种非结构化地形地貌[1-2]。虽然星球车可以根据车载传感器在星球表面进行导航控制[3-5]，但星球局部环境非常复杂，星球车仍然面临着在行进过程中发生倾覆的风险。因而，研究星球车在非结构化地貌行进过程中的稳定性，对于星球车任务的开展尤为重要。

针对车辆行进稳定性的研究较多，Chen等[6]建立车辆动力学模型，使用根轨迹法针对车辆转向工况进行分析，证明根轨迹法可以描述车辆稳定性。Sun等[7]通过建立车辆7自由度动力学模型分析车辆行进稳定性，得出可以通过降低车体质心高度等方法来增加车辆行进稳定性。Liu等[8]分析了横向力和力矩对高速行驶车辆稳定性的影响，得出可以通过优化车辆参数以改善车辆稳定性。Pan等[9]使用自适应模糊PID控制系统增强车辆操纵性和稳定性。Liu等[10]将力矩匹配算法应用于车辆稳定性控制算法之中，结果表明该算法可以提升车辆行进稳定性。

上述文献主要针对地面车辆稳定性进行分析，目前针对星球车稳定性研究较少。Kilitd等[11]提出一种三悬架式星球车，建立其运动学模型，并以星球车运动过程中倾斜角度为评价标准，分析了星球车的稳定性。Sreenivasa[12]使用稳定裕度法一种四驱星球车稳定性。Iagnema[13]针对可重构机器人稳定性优化问题进行分析，得出可重构机器人结构稳定裕度较非可重构机器人稳定裕度提升37.1%。但上述主要研究对象是四驱星球车，而目前星球车为六轮驱动。邹怀武等[14]针对嫦娥三号巡视器在转移过程中的稳定性进行了分析。

星球表面环境复杂，存在坡面、下坡道、障碍、凹坑等多种地形环境，而星球车没有直接有效的传感设备来准确地估计地形，存在因恶劣的地形环境而造成星球车发生倾覆的风险。针对以上问题，本文提出通过使用稳定角来衡量星球车在恶劣环境下的行进稳定性。首先，使用混合坐标系法建立星球车运动学模型；然后，建立星球车稳定角模型来衡量星球车行进过程中整车稳定性；最后，使用Adams软件搭建星球典型工况，并采用Adams和Matlab/Simulink软件建立联合仿真平台，对星球车在典型工况下行驶的整车稳定性进行分析，并验证本文提出的稳定性分析方法。

2 运动学建模与分析

星球车结构如图1所示，由车厢、差速器、夹角调节机构、主摇臂、副摇臂、离合器、车轮转向机构、车轮以及车轮驱动机构组成。夹角调整机构、车轮转向机构以及驱动机构为主动关节，通过接收控制指令进行调节。差速器以及离合器为被动关节，其关节转动角度根据当前行驶地形被动调节。其中，离合器包括制动和释放2种工作模式。

依据星球车结构示意图，搭建星球车运动学模型。星球车坐标系如图2所示，定义整车质心坐标系为O0，z轴为前进方向，x轴为竖直方向，y轴满足右手定则。由于星球车相对于质心坐标系O0的y轴一侧对称，在此，仅描述 -y一侧的坐标系。星球车所有杆件坐标系的原点都位于杆件的质心，关节i通常包含坐标系O^i以及坐标系Oi，两坐标系分别隶属于两个相连的杆件。初始状态下，坐标系O^i与坐标系Oi的位姿重合，因此，在图中将O^i省略。Ocm表示为星球车车厢质心坐标系，其与O0重合。差速器可以简化为两个旋转关节，分别表示为差速器轴1、差速器轴2与车厢的连接关节，记作坐标系Od1以及Od2。 由于坐标系O^d1和O^d2均属于车厢，其位姿始终相同，因而将其简化为O^d。 差速器的2个旋转关节的运动约束关系为d1=-d2=d/2。 其中，dii=1，2( )是关节的转动角度，d是差速器轴1相对于差速器轴2的转动角度。夹角调整机构可以简化为两个旋转关节，分别为前后主摇臂与差速器相连的关节，记作坐标系 Ohfi、Ohrii=1，2( )。 由于坐标系Ohfi、Ohrii=1，2( )， 均属于差速器轴 i， 其位姿总是重合，因而将其简化为。 夹角调整机构i的两关节运动约束关系为 hfi=-hri/2( i =1，2)。 其中，为关节的旋转角度。 Obi( i =1，2)是 离 合 器 i的 坐 标 系，bi( i =1，2)为离合器关节 i的旋转角度。Oti( i=1，…，6)是车轮i的转向机构关节坐标系， ti( i=1，…，6)为车轮i的转向机构旋转角度。 Owi( i=1，…，6)为车轮i驱动关节坐标系，wi( i=1，…，6)是驱动关节转动角度。

图2 星球车坐标系示意图Fig.2 Coordinate frames of the planetary rover

坐标系Oi相对于坐标系Oi-1的位置与姿态变换矩阵可以表示为式(2)、(3)：

坐标系Oi-1与坐标系Oi之间的变换矩阵为式(4)：

式中，Z13表示一个1×3的零向量矩阵。因此，星球车坐标系之间的相对关系可以通过式(3)和式(4)变换矩阵得出。

根据上述已搭建的运动学模型，可以求解得到星球车各部件之间的相对位姿关系。Tci，cm表示在t时刻车轮质心到车厢质心坐标系的变换矩阵。

其中，离合器转动角度bj以及差速器转动角度dj可以通过车载传感器获得。

通过计算变换矩阵，可以得到星球车车轮质心在车厢质心坐标系中的位置矩阵Tci，cm。

3 稳定角模型

本文结合六驱星球车行进缓慢这一特点，提出稳定角计算模型，用以计算星球车在坡道转移过程与星球表面非结构化地形行驶过程中整车稳定性的变化。

为了便于分析星球车稳定性，定义全局坐标系Ot。 在t时刻，Ot的坐标系原点与车厢质心坐标系原点重合；Ot坐标系的x轴方向与重力方向平行且相反；z轴方向与水平面平行，并指向星球车车厢前板；y轴满足右手定则。OR为星球车整车质心坐标系，其与星球车杆件质量以及星球车构型有关。因此，假定OR相对于车厢质心的位置不变。

星球车稳定角计算模型示意图如图3所示。定义 βi为星球车稳定角，其中 i=13、14、36、46，分别表示为车轮1和车轮3、车轮1和车轮4、车轮3和车轮6、车轮4和车轮6支撑边对应的稳定角，整车稳定角为其最小值。以车轮13稳定角为例，定义OR的坐标为 [0 0 0]。Og为星球车质心重力方向上任意一点，在此取 Og为[-1 0 0]。 车轮 1质心坐标 P1定义为[x1y1z1]，车轮 3质心坐标 P3定义为[x3y3z3]。Ox为Og向O1O3OR平面投影的垂点，其坐标定义为 [ x y z]，向量Pxg垂直于平面 O1O3OR。 因此，向量 Pxg分别与 Px1、Px3、PxR正交，由此可以求得Ox的坐标。通过获得的星球车车载陀螺仪以及关节角度传感器数据，结合公式(5)、(6)，可以得到向量 Px1、Px3、PxR， 其中 Px1、Px3、PxR分别表示为 Ox坐标与坐标 O1、O3、OR之间的向量关系。此时稳定角为PxR与PRg的夹角。稳定角越大，证明其对于崎岖地形的适应性越好，稳定角越接近0，此刻星球车稳定性越不足，继续行进存在倾覆的风险。

稳定角 β14、β36、β46求解方法与 β13的求解方法一致。因此，星球车整车稳定角βm为式(7)：

4 仿真分析

图3 稳定角模型Fig.3 Stability angle model

星球车稳定性主要受地形和星球车悬架机构构型影响，而星球车在松软地面地沉陷的情况，对星球车悬架机构构型及稳定性影响较小，为了分析星球车在坡道转移过程以及星球非结构化地面行进过程中的稳定性，本文使用Adams建立星球车多体动力学模型、星球表面非结构化硬质地形模型、着陆器平台以及坡道模型，使用 Matlab/Simulink建立星球车整车稳定角计算模型。由于星球表面地形复杂，沙石广泛分布，因而在行驶过程中有时需要将车体进行抬升，标称状态下，车体质心高度为300 mm。本文针对垂直越障以及坡面爬升等非结构化地形行驶工况，在车体质心调整至500 mm情况下，讨论星球车行进过程稳定性。

4.1 坡道转移工况

根据着陆器坡道设计方案[15]，建立如图4所示的星球车坡道转移极端工况。着陆器平台俯仰角为8°倾角，坡道角为 32.4°，两坡道异面角6.7°，星球车驶离坡道至星球表面，整车行进速度为50 m/h，车轮速度 5.25°/s，坡道摩擦系数为0.1。初始时刻，星球车位于着陆器平台上，随着车轮驱动，星球车通过坡道，到达星球表面，开始任务。

图4 坡道转移工况Fig.4 Rampway driving condition

仿真所得坡道转移工况稳定角变化曲线如图5所示。星球车车厢质心高度为300 mm，初始时刻星球车整车稳定角为43.69°，随着星球车继续前进，稳定角呈现减小的趋势。227.5 s时星球车完全位于坡道上并准备进行登陆运动，此时稳定角达到最小为23.23°。随着登陆运动的进行，星球车稳定角逐渐增加，最终星球车完全位于星球表面，此时稳定角恢复初始值。

图5 坡道转移工况稳定角曲线Fig.5 Curve of stability angle for rampway driving condition

4.2 星球车垂直越障工况仿真

星球车垂直越障工况如图6所示。星球车车厢质心高度为500 mm，星球车最大垂直越障高度为车轮半径高度[16]，星球车车轮半径为150 mm。设定障碍物高度为150 mm，整车行进速度为100 m/h，车轮速度为 10.5°/s，地面摩擦系数为0.3，星球车左侧各车轮依次越过障碍。

图6 垂直越障工况Fig.6 Vertical obstacle crossing condition

图7 垂直越障工况稳定角曲线Fig.7 Curve of stability angle for vertical obstacle crossing condition

仿真结果如图7所示，图7为垂直越障工况稳定角变化曲线。初始时刻稳定角为37.76°，随着车轮驱动，左侧各车轮依次爬越障碍。17.5 s时，左侧前轮行驶于障碍物上，此时稳定角降低到35.68°。44 s时，左侧中轮行驶于障碍物上，此时稳定角降低到33.22°。73 s时，左侧全部车轮于障碍物上，此时稳定角降低到30.75°，为整个运动过程中稳定角最小值。随着车轮离开障碍物，稳定角逐渐提升，最终恢复初始值37.86°。

4.3 爬坡工况

星球车爬坡工况如图8所示。星球车车厢质心高度为500 mm，整车行进速度为100 m/h，车轮行进速度为10.5°/s，地面摩擦系数为1。星球车初始位置为平地，分别驶入坡度为 20°、25°、30°、35°、40°的斜坡。

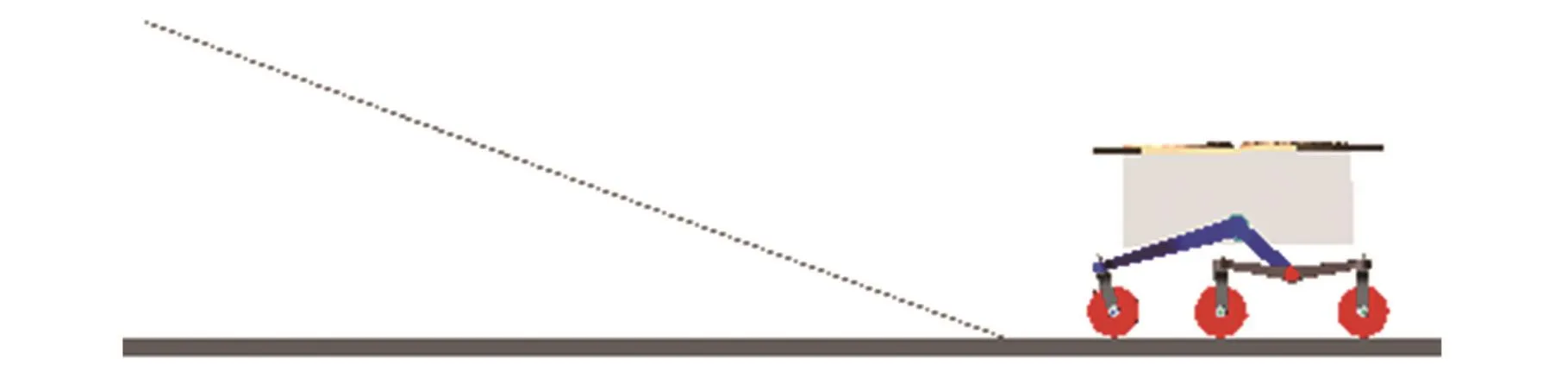
图8 爬坡工况Fig.8 Climbing condition

仿真所得爬坡工况稳定角变化曲线如图9所示。星球车分别进行不同坡度爬坡仿真。当车轮与坡面开始接触时，稳定角开始降低；当星球车完全位于坡面上时，稳定角达到最小；在坡面行驶时，稳定角保持不变。由图9可知，星球车行驶在坡度为 20°、25°、30°、35°坡度的斜坡时稳定角分别为 24.6°、19.54°、14.48°以及 9.41°。 星球车40°斜坡爬坡时虽然前两轮可以顺利爬升，但此时稳定角已接近0°，后轮继续爬升，星球车发生倾覆。由仿真可得，星球车爬坡运动可以安全通行20°、25°、30°、35°的斜坡。 由于星球车可以爬升35°的斜坡且无法爬升40°斜坡，因而以1°为间隔，分析星球车极限爬升坡度。

图9 爬坡工况稳定角曲线Fig.9 Curve of stability angle for climbing condition

图10 为星球车爬升36°斜坡工况稳定角变化曲线，通过曲线可以看出，80.7 s时整车稳定角为0.4°，随后整车发生倾覆，因而星球车极限爬升角度为35°。

图10 36°斜坡行驶稳定角变化曲线Fig.10 Curve of stability angle for 36-degree slope driving

5 结论

1)稳定角计算模型分析表明，星球车在坡道转移极端工况下，稳定角最小为23.23°，星球车可以稳定安全地完成转移；

2)由星球车在车体抬升构型下对垂直越障进行的仿真可知，稳定角最小为30.75°，星球车可以稳定安全地完成越障；

3)由星球车在车体抬升构型下对不同坡度的斜坡进行的爬坡仿真可知，星球车稳定性随着坡度的增加而减小，当稳定角接近0°时，继续行进星球车将发生倾覆，星球车极限爬坡角度为35°。

综上所述，本文所提出的稳定角计算模型可以用于星球车在非结构化环境行驶过程中的稳定性计算，以实时监测星球车行驶的安全性。